Viele glauben, dass nur die Quantenphysik komplizierter sein kann als die klassische Physik. Es ist jedoch viel schwieriger, Systeme zu untersuchen, die sich sozusagen an der Schnittstelle dieser beiden Welten befinden. Wenn einem Quantensystem immer mehr Teilchen hinzugefügt werden, verliert es seine Quanteneigenschaften und verwandelt sich in ein klassischeres. Dieser Prozess wird als quantenklassischer Übergang bezeichnet. Klassische Computer werden nicht ausreichen, um ein solches System zu untersuchen, da Wissenschaftler des Los Alamos National Laboratory einen eigenen Algorithmus vorgeschlagen haben, der zusammen mit Quantencomputern aus einigen hundert Qubits die Geheimnisse des quantenklassischen Übergangs lösen kann. Wie funktioniert der Algorithmus, warum bedeuten weniger Formeln besser und welche Anwendung dieses Algorithmus in der Praxis? Dies und nicht nur wir lernen aus dem Bericht der Forschungsgruppe. Lass uns gehen.
Studienbasis
Ein quantenklassischer Übergang ist, wenn er übertrieben ist, ein Dekohärenzprozess, wenn ein Quantensystem seine Kohärenz verliert, dh klassische Merkmale annimmt. Dieser Prozess kann aus einer Reihe von Gründen auftreten, von denen der offensichtlichste die Wechselwirkung des Quantensystems und der Umgebung ist. Es wird auch angenommen, dass dieser Prozess der Stein ist, auf den der Prozess der Realisierung eines Quantencomputers stößt.
Es gibt viele Methoden zur Bekämpfung der Dekohärenz, eine ist unterhaltsamer als die andere, aber insgesamt können sie in zwei Kategorien unterteilt werden: Isolation und Implementierung. Im ersten Fall versuchen Wissenschaftler, das Quantensystem mit sehr niedrigen Temperaturen und / oder Hochvakuum von der Umgebung zu isolieren. Im zweiten Fall werden Korrekturen (Code) in die Algorithmen der Quantenberechnung eingeführt, die gegenüber Fehlern aufgrund von Dekohärenz beständig sind. Diese Methoden funktionieren, niemand bestreitet dies, aber sie sind nicht sehr skalierbar. Wissenschaftler können Atome für eine Weile in einem Überlagerungszustand halten, wenn Umwelteinflüsse minimiert werden. In größerem Maßstab geht jedoch in der Regel alles zur Hölle.
Während einige kluge Leute in weißen Kitteln nach Wegen suchen, mit Dekohärenz umzugehen, suchen andere nach Werkzeugen, um sie zu untersuchen. Wenn Sie Ihren Feind besiegen wollen, kennen Sie ihn vom Sehen, wie sie sagen.
Bevor wir in den Strom von Formeln und Erklärungen bezüglich des von Wissenschaftlern entwickelten Algorithmus eintauchen, lohnt es sich, einen kurzen Zeitsprung zu machen. Robert Griffiths, ein amerikanischer Physiker an der Carnegie Mellon University, schlug 1984 eine Theorie der sequentiellen Geschichte (Ereignisse) vor: Die klassische Physik steht der Quantenmechanik nahe, und die Quantenmathematik kann die Wahrscheinlichkeiten großräumiger und subatomarer Phänomene berechnen, die sich nicht auf Messergebnisse, sondern auf physikalische beziehen Systemstatus. Mr. Griffiths gibt als Beispiel Fotos von Bergen, die aus verschiedenen Blickwinkeln aufgenommen werden können, und macht dann ein Bild von einem echten Berg daraus. Im Fall der Quantenphysik ist es möglich, einen Messparameter zu wählen, aber es funktioniert nicht, zwei Messungen zu kombinieren, um vor der Messung ein vollständiges Bild eines Teilchens zu erstellen. Vor dem eigentlichen Prozess der Messung der realen Position und des Impulses existiert dieser einfach nicht.
Robert GriffithsVerwirrt und ein wenig vom Dach gesprengt, aber das ist noch nicht alles. 1989 stellten Murray Gell-Mann und James Hartl ihre eigenen auf der Grundlage der Griffiths-Theorie vor. Ihrer Meinung nach kann das gesamte Universum als ein einziges Quantensystem ohne externe Umgebung betrachtet werden. Wenn ja, dann tritt Dekohärenz innerhalb des Systems auf, und das Ergebnis seiner Aktivität sind quasiklassische Domänen - Sätze von sequentiellen Historien, die vor dem Hintergrund von grobem Korn aufgrund von Dekohärenz nicht zu unterscheiden sind.
Diese Theorien halfen, einige Probleme und Paradoxien in der Quantenmechanik zu lösen, aber nicht alle. Die Forscher glauben, dass die Ergebnisse ihrer Vorgänger nicht weit verbreitet sind, da die Berechnungen nicht trivialer Systeme (z. B. diskrete Systeme mit erkennbarer Größe oder kontinuierliche Systeme, die keine ungefähre Beschreibung durch genau lösbare Integrale zulassen) äußerst kompliziert sind. Mit anderen Worten, diese Theorien sind gut, aber nur in einfachen Fällen.
In den letzten Jahren hat sich die Entwicklung von Quantentechnologien stark beschleunigt, und es sind
variierende quantenklassische Hybridalgorithmen (
VHQCA ) erschienen, die verschiedene Aufgaben (Factoring, Suche nach Grundzuständen usw.) bewältigen können.
In der Arbeit, die wir heute betrachten, beschreiben Wissenschaftler ihren VHQCA-Algorithmus für sequentielle Geschichten. Laut den Forschern übertrifft ihr Algorithmus die klassischen Methoden in vielen Parametern, einschließlich der Größe der untersuchten Systeme.
Marathon der Formeln (theoretische Grundlage)
Wir hatten bereits einen historischen Exkurs und jetzt lohnt es sich, sich ein wenig mit der Berechnungsgrundlage des Algorithmus vertraut zu machen, bevor wir die Ergebnisse seiner Arbeit betrachten.
Die Basis von sequentiellen Geschichten (CH) ist die Geschichte von
Y α ist eine Folge von Eigenschaften in einer Folge von Zeiten
t 1 <
t 2 <... <
t k :
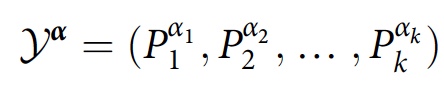
wobei
P α j j aus dem Satz von Projektoren
P j ausgewählt ist , die zum Zeitpunkt
t j summiert werden.
Wissenschaftler geben ein anschauliches Beispiel: Ein Photon passiert mehrere Beugungsgitter und trifft dann auf den Bildschirm. In einer solchen Situation kann die Geschichte ein Photon sein, das durch einen Spalt im ersten Gitter, einen anderen Spalt im zweiten usw. geht. Daher gibt es einige Interferenzen zwischen solchen Geschichten. Und da es Hindernisse gibt, ist es unmöglich, die Wahrscheinlichkeiten verschiedener Geschichten klassisch zu addieren, um eine korrekte Vorhersage des Punktes zu erreichen, an dem das Photon auf den Bildschirm trifft.
Das CH-Framework bietet Werkzeuge zur Bestimmung, wann die Story-Familie
F = {
Y α } Interferenzen aufweist, was nicht immer offensichtlich ist. Es definiert auch einen Klassenoperator:
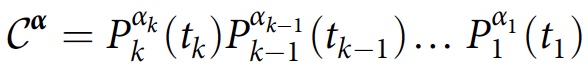
Dies ist ein zeitlich geordnetes Produkt der Projektionsoperatoren in der Geschichte von
Y α . Wenn das System anfänglich durch eine Dichtematrix ρ beschrieben wird, ist der Grad der Interferenz oder Überlappung zwischen den Historien
Yα und
Yα ' gleich:
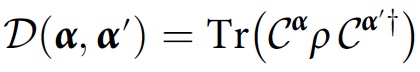
Dieser Wert wird als Dekohärenzfunktion bezeichnet. Die Konsistenzbedingung für die Story-Familie
F sieht in diesem Fall folgendermaßen aus:
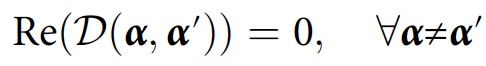
Nur wenn diese Bedingung erfüllt ist,
ist die Wahrscheinlichkeit für die Geschichte von
Y α D (
α ,
α ). Für einfachere Berechnungen kann eine andere Bedingung angewendet werden:
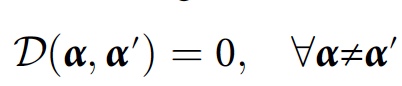
Wissenschaftler sagen, dass es für einen numerischen Algorithmus äußerst nützlich sein wird, die ungefähre Konsistenz unter Berücksichtigung geringfügiger Interferenzen zu berücksichtigen:
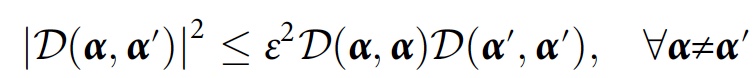
Um die Konsistenz zu untersuchen, die sich ausschließlich aus der Dekohärenz (d. H. Aufzeichnungen in der Umgebung) ergibt, schlugen die Forscher eine Methode vor, die stattdessen eine Teilspur über
E führt , das ein Teilsystem der Umgebung ist:
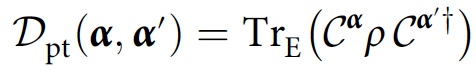
Mit dieser Änderung sieht die Konsistenzbedingung folgendermaßen aus:
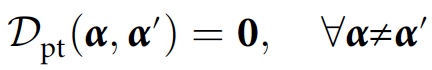
Dabei ist 0 die Nullmatrix. Anstatt das Fehlen von Umweltstörungen anzuzeigen, zeigt Konsistenz das Vorhandensein / Fehlen von Widersprüchen in den Aufzeichnungen von Geschichten in der Umwelt an.
Bild Nr. 1: Ein Story-Verzweigungsschema für k Zeitschritte.Angesichts des Marathons der Formeln und des Verständnisses sequentieller Geschichten weisen die Wissenschaftler auf die Tatsache hin, dass klassische numerische Schemata für CH die Aufgabe nicht bewältigen können.
Das Bild oben zeigt ein Beispiel, in dem es Geschichten über das Aggregat der n-ten Anzahl von Partikeln mit 1/2 Spin für
k Zeitschritte gibt. Die Anzahl der Geschichten beträgt 2
nk , daher gibt es ~ 2
2 nk funktionale Elemente der Dekohärenz. Zusätzlich erfordert die Schätzung jedes Funktionselements der Dekohärenz
D (
α ,
α ' ) das Äquivalent einer Hamilton-Simulation des Systems, d. H. Eine Multiplikation von 2
n × 2
n Matrizen. Dies bedeutet, dass moderne Cluster Hunderte von Jahren benötigen, um die Konsistenz einer Familie von Geschichten mit
k = 2 Zeitschritten und
n = 10 Drehungen zu berechnen.
VCH-Hybridalgorithmus
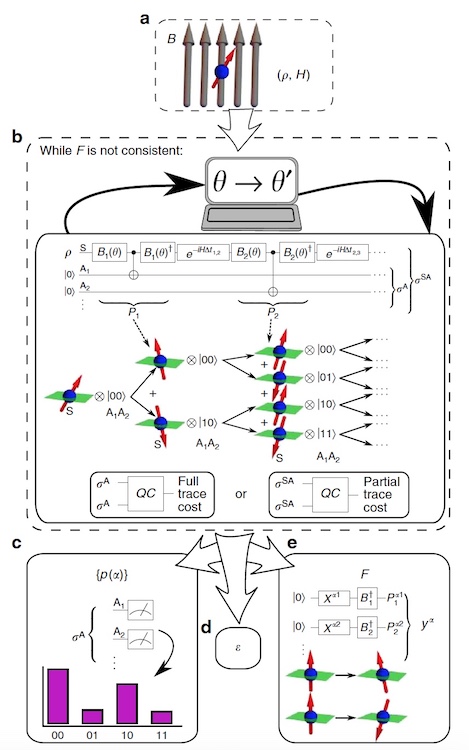Bild 2: VCH-Blockdiagramm.Wissenschaftler nannten ihren VHQCA-Algorithmus VCH (Variable Sequential Stories). Der VCH verwendet als Eingabe das physikalische Modell (d. H. Den Anfangszustand
ρ und den Hamilton-
Wert H ) und einen
Ansatz * für die Arten von Projektoren, die berücksichtigt werden müssen.
Ansatz * ist eine Vermutung darüber, wie die Lösung der Gleichung aussehen sollte und welche Form sie haben sollte.
Die folgenden Daten sind als resultierende Daten verfügbar:
- Familie von Geschichten F , die (ungefähr) eine vollständige und / oder teilweise Spur in Form von Projektionsoperatoren ist, die auf einem Quantencomputer erstellt wurden;
- Wahrscheinlichkeiten der wahrscheinlichsten Geschichten von Y α in F (Entschuldigung für das Wortspiel);
- Schätzung des Konsistenzparameters ε .
Der VCH enthält einen Parameteroptimierungszyklus, in dem ein Quantencomputer eine Kostenfunktion auswertet, die die Familienfehlanpassung quantifiziert, während der klassische Optimierer die Familie anpasst (d. H. Die Projektoreinstellungen ändert), um die Kosten zu senken.
Um die Kosten zu berechnen, muss berücksichtigt werden, dass die Elemente der Dekohärenzfunktion eine positive semidefinite Matrix bilden. Diese Eigenschaft wird in VCH verwendet, um
D im Quantenzustand σ
A zu codieren, dessen Matrixelemente ⟨α | sind
σ A |
α ' ⟩ =
D (
α ,
α' ).
2b zeigt eine Quantenschaltung, die
σ A durch Transformieren des Anfangszustands
ρ ⊗ | vorbereitet 0〉 〈0 | in
SA- Systemen (wobei
S das interessierende physikalische System modelliert und
A ein Hilfssystem ist) auf den Zustand
σ SA , dessen Grenzwert
σ A ist.Zur Konsistenz der vollständigen Spur der Matrix wird ein globales Konsistenzmaß eingeführt, das quantitativ bestimmt, wie weit
σ A von der Diagonale entfernt ist, was als Funktion der Kosten dient:
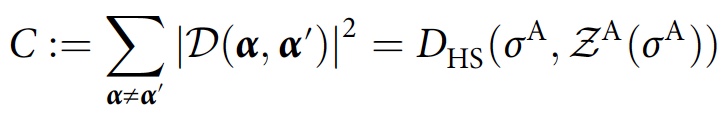
Dabei ist
D HS der Hilbert-Schmidt-Abstand und
Z A (
σ A ) die phasenfreie Version von
σ A (alle nicht diagonalen Elemente werden auf Null gesetzt)
.Diese Größe tendiert genau dann zu Null, wenn
F konsistent ist. Für den Fall einer Teilspur wird eine ähnliche Kostenfunktion erhalten, wobei jedoch
σ A durch
σ SA ersetzt wird :
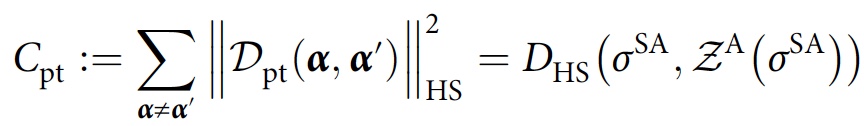
Der Parameteroptimierungszyklus führt zu einer annähernd konsistenten Familie von Geschichten
F , wobei der Konsistenzparameter
& egr; als Teil der Endkosten von oben begrenzt wird.
2c zeigt die Wahrscheinlichkeitsgenerierung für die wahrscheinlichsten Geschichten durch wiederholtes Vorbereiten von σA und Messen auf Standardbasis, wobei die Messfrequenzen die Wahrscheinlichkeiten angeben.
2e zeigt, wie eine Reihe von Projektionsoperatoren für einen bestimmten Verlauf in
F vorbereitet wird.
Versuchsergebnisse
Es wurden mehrere verschiedene Experimente unter Verwendung des VCH-Algorithmus durchgeführt. Wir werden zwei betrachten - einen Spin in einem Magnetfeld und ein chirales Molekül.
Spin in einem Magnetfeld
Bild Nr. 3Im ersten Experiment haben wir zwei Zeitverläufe eines Teilchens mit Spin 1/2 im Magnetfeld
Bz betrachtet , dessen Hamilton-
Wert H = -
γBσ z ist . Die Geschichten, die wir betrachten, haben einen Zeitschritt Δt zwischen dem Anfangszustand und dem ersten Projektor sowie zwischen dem ersten und dem zweiten Projektor. Darüber hinaus ist zu beachten, dass nur Projektoren auf der
xy- Ebene der Bloch-Kugel berücksichtigt werden.
Das obige Bild zeigt das Kostendiagramm für den Quantenprozessor ibmqx5 sowie für den Simulator, dessen Genauigkeit durch Überlagerung derselben endgültigen Statistiken, die mit dem Quantenprozessor erfasst wurden, eingeschränkt wurde. Mehrere Tiefs, die beim Ausführen von VCH auf ibmqx5 gefunden wurden, überlappen das Diagramm. Da diese Minima theoretisch konsistenten Familien recht gut entsprechen, ist dies der Erfolg von VCH in der Praxis.
Chirales Molekül
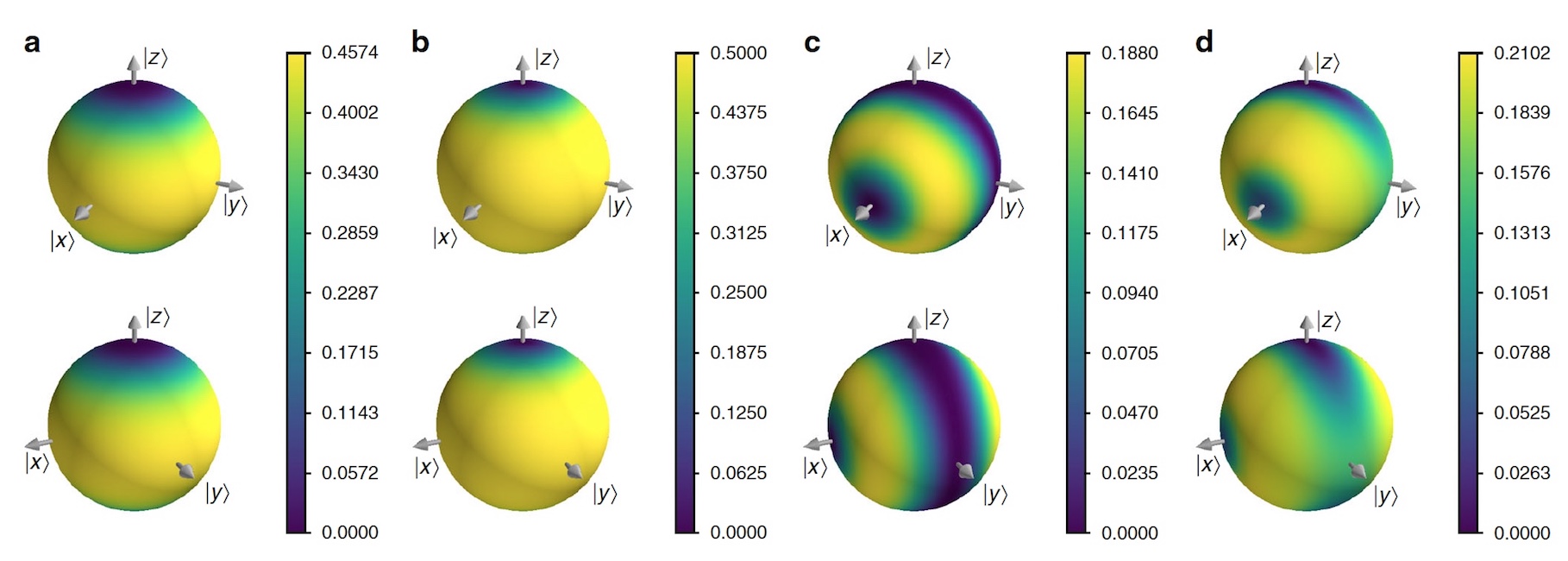Bild Nr. 4Das chirale Molekül wurde für praktische Experimente ausgewählt, da dies eine hervorragende Möglichkeit ist, die Anwendung von VCH zu bestimmen. Das chirale Molekül wurde als zweistufiges System modelliert, in dem die Chiralitätszustände rechts | R〉 und links | L〉 als | R⟩ / | L⟩ = | +⟩ / | -⟩ = 1 / √2 * (| 0⟩ ± | beschrieben werden) 1⟩).
Ein isoliertes chirales Molekül tunnelt zwischen | R⟩ und | L⟩, aber Wissenschaftler spekulieren, dass es sich in einem Gas befindet, in dem Kollisionen mit anderen Molekülen Informationen über die Chiralität des Moleküls an seine Umgebung übertragen. Diese Informationsübertragung wird durch Drehung um einen Winkel
θ x um die
x- Achse eines mittleren Qubits modelliert, das von der Chiralität des Systems gesteuert wird.
Die Wissenschaftler betrachten dann einfache Familien stationärer Geschichten, bei denen eine Reihe von Projektoren alle fünf Male derselben Basis entspricht (zur Vereinfachung der Modellierung wurde festgestellt, dass das Molekül fünfmal mit anderen Molekülen kollidiert). Unter der Annahme, dass
θz der Präzessionswinkel aufgrund des zeitlichen Tunnelns zwischen Kollisionen ist, ist es möglich, die Konkurrenz zwischen Dekohärenz und Tunneln zu untersuchen. Das Bild oben zeigt die Ergebnisse dieser Simulation.
Wissenschaftler stellen eine merkwürdige Tatsache fest: Es gibt einen Übergang vom Quantenregime, bei dem die Chiralität nicht sequentiell ist, zum klassischen Regime, bei dem die Chiralität sowohl sequentiell als auch über die Zeit stabil ist.
Um die Nuancen der Studie genauer kennenzulernen, empfehle ich Ihnen, den
Bericht von Wissenschaftlern und
zusätzliche Materialien zu lesen.
Nachwort
Diese Arbeit hat einen neuen Algorithmus demonstriert, der in Verbindung mit bestehenden und zukünftigen Quantencomputern einen so komplexen und komplizierten Prozess wie einen quantenklassischen Übergang am besten beschreiben kann. Die Untersuchung dieses Phänomens ist von großer Bedeutung, wenn wir jemals einen realen, funktionierenden und effizienten Quantencomputer schaffen wollen, dessen Betrieb nicht durch Dekohärenz beeinträchtigt wird.
Der VCH-Algorithmus befindet sich in der Anfangsphase der Entwicklung, zeigt jedoch bereits seine Leistung. Wissenschaftler wollen es in Zukunft natürlich verbessern. Wie dem auch sei, die Aussichten für eine frühzeitige Implementierung des Quantencomputers bleiben nicht nur auf dem gleichen Niveau, sondern wachsen mit jeder solchen Studie.
Vielen Dank für Ihre Aufmerksamkeit, bleiben Sie neugierig und haben Sie eine gute Arbeitswoche, Jungs! :) :)
Vielen Dank für Ihren Aufenthalt bei uns. Gefällt dir unser Artikel? Möchten Sie weitere interessante Materialien sehen? Unterstützen Sie uns, indem Sie eine Bestellung
aufgeben oder Ihren Freunden empfehlen, einen
Rabatt von 30% für Habr-Benutzer auf ein einzigartiges Analogon von Einstiegsservern, das wir für Sie erfunden haben: Die ganze Wahrheit über VPS (KVM) E5-2650 v4 (6 Kerne) 10 GB DDR4 240 GB SSD 1 Gbit / s von $ 20 oder wie teilt man den Server? (Optionen sind mit RAID1 und RAID10, bis zu 24 Kernen und bis zu 40 GB DDR4 verfügbar).
Dell R730xd 2 mal günstiger? Nur wir haben
2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2,6 GHz 14C 64 GB DDR4 4 x 960 GB SSD 1 Gbit / s 100 TV von 199 US-Dollar in den Niederlanden! Dell R420 - 2x E5-2430 2,2 GHz 6C 128 GB DDR3 2x960 GB SSD 1 Gbit / s 100 TB - ab 99 US-Dollar! Lesen Sie mehr über
den Aufbau eines Infrastrukturgebäudes. Klasse mit Dell R730xd E5-2650 v4 Servern für 9.000 Euro für einen Cent?