
Hallo habrozhiteli! „Vorhersagemodellierung in der Praxis“ deckt alle Aspekte der Prognose ab, beginnend mit den Schlüsselphasen der Datenvorverarbeitung, Datenaufteilung und den Grundprinzipien der Modelloptimierung. Alle Phasen der Modellierung werden anhand praktischer Beispiele aus dem wirklichen Leben betrachtet. In jedem Kapitel wird ein detaillierter Code in R-Sprache angegeben.
Dieses Buch kann als Einführung in Vorhersagemodelle und als Leitfaden für deren Anwendung verwendet werden. Leser ohne mathematische Ausbildung werden die intuitiven Erklärungen bestimmter Methoden zu schätzen wissen, und die Aufmerksamkeit, die der Lösung tatsächlicher Probleme mit realen Daten gewidmet wird, wird Fachleuten helfen, die ihre Fähigkeiten verbessern möchten.
Die Autoren versuchten, komplexe Formeln zu vermeiden. Das Verständnis der grundlegenden statistischen Konzepte wie Korrelation und lineare Regressionsanalyse reicht aus, um das Grundmaterial zu beherrschen. Für das Studium fortgeschrittener Themen ist jedoch eine mathematische Ausbildung erforderlich.
Auszug. 7.5. Berechnungen
In diesem Abschnitt werden Funktionen aus den Paketen R caret, earth, kernlab und nnet verwendet.
R hat viele Pakete und Funktionen zum Erstellen neuronaler Netze. Dazu gehören nnet-, neuronale und RSNNS-Pakete. Das Hauptaugenmerk liegt auf dem nnet-Paket, das grundlegende Modelle neuronaler Netze mit einer Ebene versteckter Variablen, der Gewichtsreduzierung, unterstützt und sich durch eine relativ einfache Syntax auszeichnet. RSNNS unterstützt eine Vielzahl von neuronalen Netzen. Beachten Sie, dass Bergmeir und Benitez (2012) eine kurze Beschreibung der verschiedenen neuronalen Netzwerkpakete in R haben. Dort wird auch das RSNNS-Tutorial bereitgestellt.
Neuronale Netze
Um das Regressionsmodell zu approximieren, kann die nnet-Funktion sowohl die Formel des Modells als auch die Matrixschnittstelle empfangen. Für die Regression wird die lineare Beziehung zwischen versteckten Variablen und der Prognose mit dem Parameter linout = TRUE verwendet. Der einfachste Aufruf der neuronalen Netzwerkfunktion sieht folgendermaßen aus:
> nnetFit <- nnet(predictors, outcome, + size = 5, + decay = 0.01, + linout = TRUE, + ## + trace = FALSE, + ## + ## .. + maxit = 500, + ## , + MaxNWts = 5 * (ncol(predictors) + 1) + 5 + 1)
Dieser Aufruf erstellt ein Modell mit fünf versteckten Variablen. Es wird angenommen, dass die Daten in den Prädiktoren auf einer einzigen Skala standardisiert wurden.
Um die Modelle zu mitteln, wird die avNNet-Funktion aus dem Caret-Paket verwendet, die dieselbe Syntax hat:
> nnetAvg <- avNNet(predictors, outcome, + size = 5, + decay = 0.01, + ## + repeats = 5, + linout = TRUE, + ## + trace = FALSE, + ## + ## .. + maxit = 500, + ## , + MaxNWts = 5 * (ncol(predictors) + 1) + 5 + 1)
Neue Datenpunkte werden vom Befehl verarbeitet
> predict(nnetFit, newData) > ## > predict(nnetAvg, newData)
Um die zuvor vorgestellte Methode zur Auswahl der Anzahl versteckter Variablen und des Ausmaßes der Gewichtsreduzierung durch wiederholtes Abtasten zu reproduzieren, wenden wir die Zugfunktion mit dem Parameter method = "nnet" oder method = "avNNet" an und entfernen zuerst die Prädiktoren (damit die maximale absolute Paarkorrelation zwischen den Prädiktoren nicht überschritten wird 0,75):
> ## findCorrelation > ## , > ## > tooHigh <- findCorrelation(cor(solTrainXtrans), cutoff = .75) > trainXnnet <- solTrainXtrans[, -tooHigh] > testXnnet <- solTestXtrans[, -tooHigh] > ## - : > nnetGrid <- expand.grid(.decay = c(0, 0.01, .1), + .size = c(1:10), + ## — + ## (. ) + ## . + .bag = FALSE) > set.seed(100) > nnetTune <- train(solTrainXtrans, solTrainY, + method = "avNNet", + tuneGrid = nnetGrid, + trControl = ctrl, + ## + ## + preProc = c("center", "scale"), + linout = TRUE, + trace = FALSE, + MaxNWts = 10 * (ncol(trainXnnet) + 1) + 10 + 1, + maxit = 500)
Mehrdimensionale adaptive Regressionssplines
MARS-Modelle sind in mehreren Paketen enthalten, die umfangreichste Implementierung befindet sich jedoch im Earth-Paket. Ein MARS-Modell, das die nominelle Phase des direkten Durchlaufs und Abschneidens verwendet, kann wie folgt aufgerufen werden:
> marsFit <- earth(solTrainXtrans, solTrainY) > marsFit Selected 38 of 47 terms, and 30 of 228 predictors Importance: NumNonHAtoms, MolWeight, SurfaceArea2, SurfaceArea1, FP142, ... Number of terms at each degree of interaction: 1 37 (additive model) GCV 0.3877448 RSS 312.877 GRSq 0.907529 RSq 0.9213739
Da dieses Modell in der internen Implementierung die GCV-Methode zur Auswahl eines Modells verwendet, unterscheidet sich seine Struktur etwas von dem zuvor in diesem Kapitel beschriebenen Modell. Die Zusammenfassungsmethode generiert eine umfangreichere Ausgabe:
> summary(marsFit) Call: earth(x=solTrainXtrans, y=solTrainY) coefficients (Intercept) -3.223749 FP002 0.517848 FP003 -0.228759 FP059 -0.582140 FP065 -0.273844 FP075 0.285520 FP083 -0.629746 FP085 -0.235622 FP099 0.325018 FP111 -0.403920 FP135 0.394901 FP142 0.407264 FP154 -0.620757 FP172 -0.514016 FP176 0.308482 FP188 0.425123 FP202 0.302688 FP204 -0.311739 FP207 0.457080 h(MolWeight-5.77508) -1.801853 h(5.94516-MolWeight) 0.813322 h(NumNonHAtoms-2.99573) -3.247622 h(2.99573-NumNonHAtoms) 2.520305 h(2.57858-NumNonHBonds) -0.564690 h(NumMultBonds-1.85275) -0.370480 h(NumRotBonds-2.19722) -2.753687 h(2.19722-NumRotBonds) 0.123978 h(NumAromaticBonds-2.48491) -1.453716 h(NumNitrogen-0.584815) 8.239716 h(0.584815-NumNitrogen) -1.542868 h(NumOxygen-1.38629) 3.304643 h(1.38629-NumOxygen) -0.620413 h(NumChlorine-0.46875) -50.431489 h(HydrophilicFactor- -0.816625) 0.237565 h(-0.816625-HydrophilicFactor) -0.370998 h(SurfaceArea1-1.9554) 0.149166 h(SurfaceArea2-4.66178) -0.169960 h(4.66178-SurfaceArea2) -0.157970 Selected 38 of 47 terms, and 30 of 228 predictors Importance: NumNonHAtoms, MolWeight, SurfaceArea2, SurfaceArea1, FP142, ... Number of terms at each degree of interaction: 1 37 (additive model) GCV 0.3877448 RSS 312.877 GRSq 0.907529 RSq 0.9213739
Bei dieser Ableitung ist h (·) die Scharnierfunktion. In den vorgestellten Ergebnissen ist die Komponente h (MolWeight-5.77508) bei einem Molekulargewicht von weniger als 5.77508 gleich Null (wie im oberen Teil von Abb. 7.3). Die reflektierte Scharnierfunktion hat die Form h (5.77508 - MolWeight).
Mit der Plotmo-Funktion aus dem Erdpaket können Diagramme erstellt werden, die den in Abb. 1 gezeigten ähnlich sind. 7.5. Sie können train verwenden, um das Modell mithilfe eines externen Resamplings zu konfigurieren. Der folgende Code gibt die in Abb. 1 gezeigten Ergebnisse wieder. 7.4:
> # - > marsGrid <- expand.grid(.degree = 1:2, .nprune = 2:38) > # > set.seed(100) > marsTuned <- train(solTrainXtrans, solTrainY, + method = "earth", + # - + tuneGrid = marsGrid, + trControl = trainControl(method = "cv")) > marsTuned 951 samples 228 predictors No pre-processing Resampling: Cross-Validation (10-fold) Summary of sample sizes: 856, 857, 855, 856, 856, 855, ... Resampling results across tuning parameters: degree nprune RMSE Rsquared RMSE SD Rsquared SD 1 2 1.54 0.438 0.128 0.0802 1 3 1.12 0.7 0.0968 0.0647 1 4 1.06 0.73 0.0849 0.0594 1 5 1.02 0.75 0.102 0.0551 1 6 0.984 0.768 0.0733 0.042 1 7 0.919 0.796 0.0657 0.0432 1 8 0.862 0.821 0.0418 0.0237 : : : : : : 2 33 0.701 0.883 0.068 0.0307 2 34 0.702 0.883 0.0699 0.0307 2 35 0.696 0.885 0.0746 0.0315 2 36 0.687 0.887 0.0604 0.0281 2 37 0.696 0.885 0.0689 0.0291 2 38 0.686 0.887 0.0626 0.029 RMSE was used to select the optimal model using the smallest value. The final values used for the model were degree = 1 and nprune = 38. > head(predict(marsTuned, solTestXtrans)) [1] 0.3677522 -0.1503220 -0.5051844 0.5398116 -0.4792718 0.7377222
Zwei Funktionen werden verwendet, um die Wichtigkeit jedes Prädiktors im MARS-Modell zu bewerten: evimp aus dem Erdpaket und varImp aus dem Caret-Paket (der zweite nennt den ersten):
> varImp(marsTuned) earth variable importance only 20 most important variables shown (out of 228) Overall MolWeight 100.00 NumNonHAtoms 89.96 SurfaceArea2 89.51 SurfaceArea1 57.34 FP142 44.31 FP002 39.23 NumMultBond s 39.23 FP204 37.10 FP172 34.96 NumOxygen 30.70 NumNitrogen 29.12 FP083 28.21 NumNonHBonds 26.58 FP059 24.76 FP135 23.51 FP154 21.20 FP207 19.05 FP202 17.92 NumRotBonds 16.94 FP085 16.02
Diese Ergebnisse sind im Bereich von 0 bis 100 skaliert und unterscheiden sich von den in der Tabelle angegebenen. 7.1 (das in Tabelle 7.1 dargestellte Modell hat nicht den gesamten Prozess des Wachstums und der Verkürzung durchlaufen). Beachten Sie, dass die Variablen, die auf die ersten folgen, für das Modell weniger wichtig sind.
SVM, Support-Vektor-Methode
Implementierungen von SVM-Modellen sind in mehreren R.-Paketen enthalten. Chang und Lin (Chang und Lin, 2011) verwenden die svm-Funktion aus dem e1071-Paket, um die Schnittstelle zur LIBSVM-Bibliothek für die Regression zu verwenden. Eine vollständigere Implementierung von SVM-Modellen für die Karatsogl-Regression (Karatzoglou et al., 2004) ist im Kernlab-Paket enthalten, das die ksvm-Funktion für Regressionsmodelle und eine große Anzahl von Kernfunktionen enthält. Standardmäßig wird die radiale Basisfunktion verwendet. Wenn die Werte der Kosten und der Kernparameter bekannt sind, kann die Approximation des Modells wie folgt durchgeführt werden:
> svmFit <- ksvm(x = solTrainXtrans, y = solTrainY, + kernel ="rbfdot", kpar = "automatic", + C = 1, epsilon = 0.1)
Zur Schätzung von σ wurde eine automatisierte Analyse verwendet. Da y ein numerischer Vektor ist, approximiert die Funktion offensichtlich das Regressionsmodell (anstelle des Klassifizierungsmodells). Sie können andere Kernelfunktionen verwenden, einschließlich Polynom (Kernel = "Polydot") und Linear (Kernel = "Vanilladot").
Wenn die Werte unbekannt sind, können sie durch erneutes Abtasten geschätzt werden. Im Zug wählen die Werte "svmRadial", "svmLinear" oder "svmPoly" des Methodenparameters verschiedene Kernelfunktionen aus:
> svmRTuned <- train(solTrainXtrans, solTrainY, + method = "svmRadial", + preProc = c("center", "scale"), + tuneLength = 14, + trControl = trainControl(method = "cv"))
Das Argument tuneLength verwendet 14 Standardwerte.

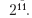
Eine Standardschätzung von σ wird durch automatische Analyse durchgeführt.
> svmRTuned 951 samples 228 predictors Pre-processing: centered, scaled Resampling: Cross-Validation (10-fold) Summary of sample sizes: 855, 858, 856, 855, 855, 856, ... Resampling results across tuning parameters: C RMSE Rsquared RMSE SD Rsquared SD 0.25 0.793 0.87 0.105 0.0396 0.5 0.708 0.889 0.0936 0.0345 1 0.664 0.898 0.0834 0.0306 2 0.642 0.903 0.0725 0.0277 4 0.629 0.906 0.067 0.0253 8 0.621 0.908 0.0634 0.0238 16 0.617 0.909 0.0602 0.0232 32 0.613 0.91 0.06 0.0234 64 0.611 0.911 0.0586 0.0231 128 0.609 0.911 0.0561 0.0223 256 0.609 0.911 0.056 0.0224 512 0.61 0.911 0.0563 0.0226 1020 0.613 0.91 0.0563 0.023 2050 0.618 0.909 0.0541 0.023 Tuning parameter 'sigma' was held constant at a value of 0.00387 RMSE was used to select the optimal model using the smallest value. The final values used for the model were C = 256 and sigma = 0.00387.
Das Unterobjekt finalModel enthält das von der Funktion ksvm erstellte Modell:
> svmRTuned$finalModel Support Vector Machine object of class "ksvm" SV type: eps-svr (regression) parameter : epsilon = 0.1 cost C = 256 Gaussian Radial Basis kernel function. Hyperparameter : sigma = 0.00387037424967707 Number of Support Vectors : 625 Objective Function Value : -1020.558 Training error : 0.009163
Als Referenzvektoren verwendet das Modell 625 Datenpunkte des Trainingssatzes (d. H. 66% des Trainingssatzes).
Das Kernlab-Paket enthält eine Implementierung des RVM-Modells für die Regression in der rvm-Funktion. Die Syntax ist der im Beispiel für ksvm dargestellten sehr ähnlich.
KNN-Methode
Das Caren-Paket knnreg nähert sich dem KNN-Regressionsmodell an; Die Zugfunktion setzt das Modell auf K:
> # . > knnDescr <- solTrainXtrans[, -nearZeroVar(solTrainXtrans)] > set.seed(100) > knnTune <- train(knnDescr, + solTrainY, + method = "knn", + # + # + preProc = c("center", "scale"), + tuneGrid = data.frame(.k = 1:20), + trControl = trainControl(method = "cv"))
Über die Autoren:
Max Kun ist Leiter der Abteilung für statistische nichtklinische Forschung und Entwicklung von Pfizer Global Er arbeitet seit über 15 Jahren mit Vorhersagemodellen und ist Autor mehrerer Spezialpakete für die R-Sprache. Die Vorhersagemodellierung in der Praxis deckt alle Aspekte der Vorhersage ab, beginnend mit den Schlüsselphasen der Datenvorverarbeitung, Datenaufteilung und Grundprinzipien
Modelleinstellungen. Alle Phasen der Modellierung werden anhand praktischer Beispiele betrachtet.
Aus dem wirklichen Leben enthält jedes Kapitel einen detaillierten Code in R.
Kjell Johnson ist seit mehr als zehn Jahren auf dem Gebiet der Statistik und Vorhersagemodellierung für die pharmazeutische Forschung tätig. Mitbegründer von Arbor Analytics, einem Unternehmen, das sich auf Vorhersagemodelle spezialisiert hat; Zuvor leitete er die Abteilung für statistische Forschung und Entwicklung bei Pfizer Global. Seine wissenschaftliche Arbeit widmet sich der Anwendung und Entwicklung statistischer Methoden und Lernalgorithmen.
»Weitere Informationen zum Buch finden Sie auf
der Website des Herausgebers»
Inhalt»
Auszug25% Rabatt auf den Gutschein für Händler -
Angewandte prädiktive ModellierungNach Bezahlung der Papierversion des Buches wird ein elektronisches Buch per E-Mail verschickt.