Weißes Rauschen zeichnet ein schwarzes Quadrat. Teil 2. Lösung

In der ersten Veröffentlichung wurde gesagt, dass es einen vergessenen Erd-s-Renyi-Satz gibt, aus dem folgt, dass in einer zufälligen Reihe der Länge N mit einer Wahrscheinlichkeit nahe 1 eine Reihe identischer Längenwerte existiert $$$\ log_2 {N}$. Die angegebene Eigenschaft einer Zufallsvariablen kann verwendet werden, um die Frage zu beantworten: "Befolgen die verbleibenden Reihen nach der Verarbeitung von Big Data das Gesetz der Zufallszahlen oder nicht?"

Die Antwort auf diese Frage wurde nicht auf der Grundlage von Tests zur Übereinstimmung mit der Normalität der Verteilung bestimmt, sondern auf der Grundlage der Eigenschaften der Restreihen selbst.

Durch das Vorhandensein oder Fehlen oder Verschieben der Häufigkeit der Verträge der gleichen Charaktere. Ich habe versucht zu veröffentlichen, um die Möglichkeiten der Verwendung dieses Tools aufzuzeigen, obwohl sich viele Fragen darüber stellten, wie dies in der Realität funktioniert, wenn Analysen in Big Data durchgeführt werden. Die Diskussion war jedoch produktiv, und der VDG- Benutzer präsentierte sogar ein reales Beispiel: „... Die dendritischen Zweige eines Neurons können als Bitsequenz dargestellt werden. Ein Zweig und dann das gesamte Neuron wird ausgelöst, wenn eine Synapsenkette an einer ihrer Stellen aktiviert wird. Das Neuron hat die Aufgabe, nicht auf weißes Rauschen zu reagieren. Soweit ich mich in Numenta erinnere, beträgt die Mindestlänge der Kette 14 Synapsen im pyramidenförmigen Neuron mit seinen 10 000 Synapsen. Und nach der Formel erhalten wir: $\ log_2 {10000} = $ 13.28$. Das heißt, Ketten mit einer Länge von weniger als 14 werden aufgrund von natürlichem Rauschen auftreten, aber das Neuron nicht aktivieren. Es ist perfekt richtig gelegt . "

Versuchen wir, den in diesem Material vorgestellten Mechanismus zu betrachten.

Die erste Veröffentlichung warf viele Fragen auf. Versuchen wir, den Mechanismus des Erds-Renyi-Theorems in diesem Artikel zu klären.

Die Lösung entstand im Zusammenhang mit dem Penny-Game- Paradoxon. Das Spiel besteht aus Folgendem: Zwei Spieler A und B werfen fünf Mal eine Münze und weisen beispielsweise "Adler" - 1, "Schwänze" - 0 zu. Spieler A wählt eine Folge von drei Werten und spricht sie aus, angenommen 001.

Spieler B wählt seine Sequenz, angenommen 100. Der Spieler, dessen Sequenz zuerst fällt, ist der Gewinner. Angenommen, 01001 ist gefallen, dh 0-100-1, was der Wahl von B entspricht. Das Paradox des „Penny-Spiels“ ist, dass Spieler B unabhängig von der von einem Spieler A gewählten Sequenz immer die Möglichkeit hat, eine Sequenz zu wählen, deren Wahrscheinlichkeit größer ist als die von Spieler A gewählte Reihenfolge. Die Gewinnmatrix von Spieler B ist in Abbildung 1 dargestellt.


Abb. 1. Die Auszahlungsmatrix für Spieler B im „Penny Game“ für fünf Schüsse.

Der Effekt dieses Paradoxons ist, dass die Zufallsreihe nicht transitiv ist, dh wenn U> R, sondern R> Q, dann bedeutet dies nicht, dass Q> U ist.

Die Konsequenz dieses Paradoxons sind die folgenden gewöhnlichen Dinge, wenn ein Spieler die Regeln einhält und die Gesetze der Wahrscheinlichkeitstheorie einhält:

1. Beim Glücksspiel gewinnt er normalerweise, dessen Kassierer mehr ist - "Crush the Bank".
2. In einem Casino gewinnt nur das Casino.
3. Wenn Sie an der Börse spielen, bestimmt nur das Glück, wie lange ein Trader bestehen bleibt, bis er sein Kapital verliert.

Die physikalische Bedeutung dieses Gesetzes, auf dem das Paradoxon „Penny Game“ basiert, ist, dass derjenige, der die Zufallssequenz mehr fortsetzen kann, den Vorteil hat. Wie im ersten Beispiel - ein Spieler, der mehr Geld hat. Bei der zweiten Option spielt das Casino mit Hunderten von Sequenzen gleichzeitig und spielt weiter, nachdem einer der Spieler das Spiel beendet hat. Ein Spiel gegen den Austausch eines Spielers ist nicht mit Millionen von Operationen an der Börse zu vergleichen.

Wie Sie sehen, wurde das erste Gesetz gezogen - BigData bestimmt die Situation im Vergleich zu lokalen Informationen.

Der zweite entscheidende Moment ist das Fehlen der Transitivitätseigenschaft von Zufallssequenzen. Die Folge davon ist die Unfähigkeit, die Situation zurückzudrängen.

Weitere Hypothese bei der Analyse von BigData:

1) Das Verständnis der Entwicklung von Ereignissen ist nur in einem solchen Umfang möglich, in dem die Folgen der untersuchten Ereignisse aufgezeichnet werden. Der Mechanismus für diesen Prozess kann wie folgt dargestellt werden. Ein Zufallsfeld ist ein Feld, in dem mehrere potenzielle Prozesse versuchen, sich selbst zu realisieren. Nach der Selbstverwirklichung hinterlässt der Prozess Änderungen, und wir versuchen, den Grad der Spuren der aufgetretenen Prozesse zu ermitteln. Abhängigkeiten werden bereits durch den Wert des Anteils der linken Ergebnisse bestimmt. Ich werde oben erklären, dass meiner Meinung nach die Art und Weise, wie die Transformationen selbst stattfinden, die Wissenschaft im Moment keine formale Definition geben kann. Wenn diese Definitionen wären, würden einige von Zenos Paradoxien aufhören, Paradoxe zu sein, und die Einheit und der Kampf der Gegensätze, die materialistische Dialektik würde aufhören, ein Postulat darin zu sein.

Ich nehme an, dass es sich nicht lohnt, die Speere von Aussagen zu brechen, dass dies eine bedeutungslose Übung ist, wenn wir den Prozess nachträglich bestimmen, da der nächste Prozess unvorhersehbar sein wird. Eine Person sieht ganz lokal, und BigData-Prozesse können Milliarden von Jahren dauern. Daher haben wir die Möglichkeit, den Mechanismus eines Prozesses im BigData-Bereich zu sehen. Hier wird interessantes Material zu den großen Werten des Universums vorgestellt.

2) Die zweite Hypothese, die aus dem Fehlen der Transitivitätseigenschaft abgeleitet werden kann, ist der Einfluss des Intervalls und der Bedingungen auf den untersuchten Prozess. Das heißt, einerseits gibt es eine Zeitkoordinate, die den untersuchten Prozess positioniert, und eine Chance, die Bedingungen zu wiederholen, unter denen unser Prozess gebildet wurde und Millionen von Aufzeichnungen eingegangen sind, ist fast unmöglich. Andererseits können die Gesetze der Kombinatorik nicht ignoriert werden. Diese Gesetze sagen uns, dass die Wahrscheinlichkeit des Auftretens einer bestimmten Kombination immer bestehen muss. Fig. 2 zeigt die Verteilung von Varianten von Ketten von N Signalen, in denen Reihen von Unterordnungen der Länge k vorhanden sind. Der Gesamtbetrag ist größer als $$$2 ^ N$, da kurze Ketten mit längeren kombiniert werden.


Abb. 2. Die Anzahl möglicher Unterordnungsvarianten von k identischen Signalen in einer Folge von N Werten.

Für Varianten, in denen Ketten länger als N / 2 vorhanden sind, sind sie gelb gefüllt, ihre Anzahl wird auf ziemlich einfache Weise durch die Formel bestimmt:



Das heißt, die entsprechenden Wahrscheinlichkeiten für Reihen mit Ketten von k> = N / 2 identischen Werten (wir werden die Wahrscheinlichkeit einer Reihe von N Werten nicht beschreiben) werden durch die Formel bestimmt:



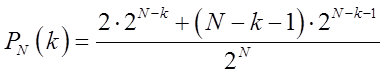
Während der Diskussion im ersten Teil stellten sich Fragen, deren Kern sich auf Folgendes beschränkte: „Wo liegen die Grenzen des weißen Rauschens?“ Hier wurde unter Berücksichtigung der Tabelle von 2 eine Hypothese zur Diskussion gemäß dem folgenden Schema gebildet.

Basierend auf dem Muavre-Laplace-Integralsatz:



Wir definieren die Intervalle für f (1,96) = 95% Wahrscheinlichkeit:



Wenn Sie sich das ansehen, spiegelt die Tabelle in Abbildung 2 das gesamte Wahrscheinlichkeitsfeld wider. Andererseits sind die Verteilungsparameter jeweils eindeutig definierbar und in Abbildung 3 dargestellt, wo wir sie als Beispiel für eine Reihe von 9 Werten zeigen. Da die Anzahl der Optionen $$$2 ^ 9 {= 512}$und für diese Anzahl von Tests finden wir Alpha.


Abb. 3. Die Grenzen der Wahrscheinlichkeitsintervalle von Unterordnungen der Länge k derselben Signale in einer Folge von 9 Werten mit einer Zuverlässigkeit von 2 Sigma (95%).

Fig. 4 zeigt die Intervalle für eine Zufallsvariable, wobei Fig. 4b die transponierte Fig. 4a ist.


Abb. 4. Intervalle zufälliger Größe für jede Unterordnung mit einer Zuverlässigkeit von 95%.

Um die Antworten auf die Fragen, wo sich das weiße Rauschen befindet, irgendwie zu strukturieren, formulierte er die bestehenden Ansätze wie folgt:

1. Weißes Rauschen wird von der Community erkannt.
2. Daten, die mit analytischen Ausdrücken formuliert werden können;
3. Informationen, die durch neuronale Netze strukturiert sind;
4. Qubits, Quantencomputer;
5. BigData
6. Wenn Big Data vorhanden ist, ist es durchaus möglich, dass Hyperdaten vorhanden sind.

Für die vorgeschlagene Strukturierung war der Anhaltspunkt die Idee von O. V. Filatov „Definition einer zufälligen binären Sequenz als kombinatorisches Objekt. Berechnung von zusammenfallenden Fragmenten in zufälligen binären Sequenzen “ über das Verhalten von Fragmenten einer Sequenz, die dem Verhalten von Partikeln in der Mikrowelt ähneln.

Die Qubits, die eine dreidimensionale Struktur haben, geben Anlass zu der Annahme, dass das Strukturschema ein dreidimensionales Modell haben sollte. Mehrere Schichten, die von der Community erkannt werden, implizierten die Überlagerung des Modells, und wenn man all dies kombiniert, ist das eleganteste Schema in Form eines Toroids möglich (Abbildung 5).


Abb. 5. Die Annahme der Struktur der Daten bei der Abbildung von Zufallsvariablen auf den Raum (Bilder aus dem Internet).

Bei der Weiterentwicklung der Argumentation stellen wir fest, dass in Abbildung 3 alle Frequenzen gerade Zahlen sind. Dies ist eine Folge der Symmetrie der Daten "0-1". Die Symmetrie zufälliger Daten spiegelt sich in Solomon Wolf Golombs Postulaten des Golomb wider. Basierend auf der Forschung Filatova O.V. „Ableitung von Formeln für die Postulate von Golomb. Eine Möglichkeit, eine Pseudozufallssequenz aus Mises-Frequenzen zu erstellen. Die Grundlagen der „Kombinatorik langer Sequenzen“ verwenden das Konzept einer Halbwelle. Ich glaube, dass dieser Aspekt bei der Untersuchung des weißen Rauschens von Bedeutung ist, da er mit Parametern wie der Zeilenlänge verbunden ist.

Angesichts der Eigenschaften zufälliger Prozesse kann eine Welle mit weißem Rauschen verschiedene Eigenschaften annehmen, einschließlich des Fehlens einer Wellensymmetrie und der möglichen Nichteinhaltung des Noether-Theorems . In der physikalischen Welt gibt es jedoch Prozesse wie die Bildung von Schaum einer Brandungswelle (Abbildung 6). Wir haben also allen Grund, ungewöhnliche Parameter für Wellen mit weißem Rauschen zuzulassen.


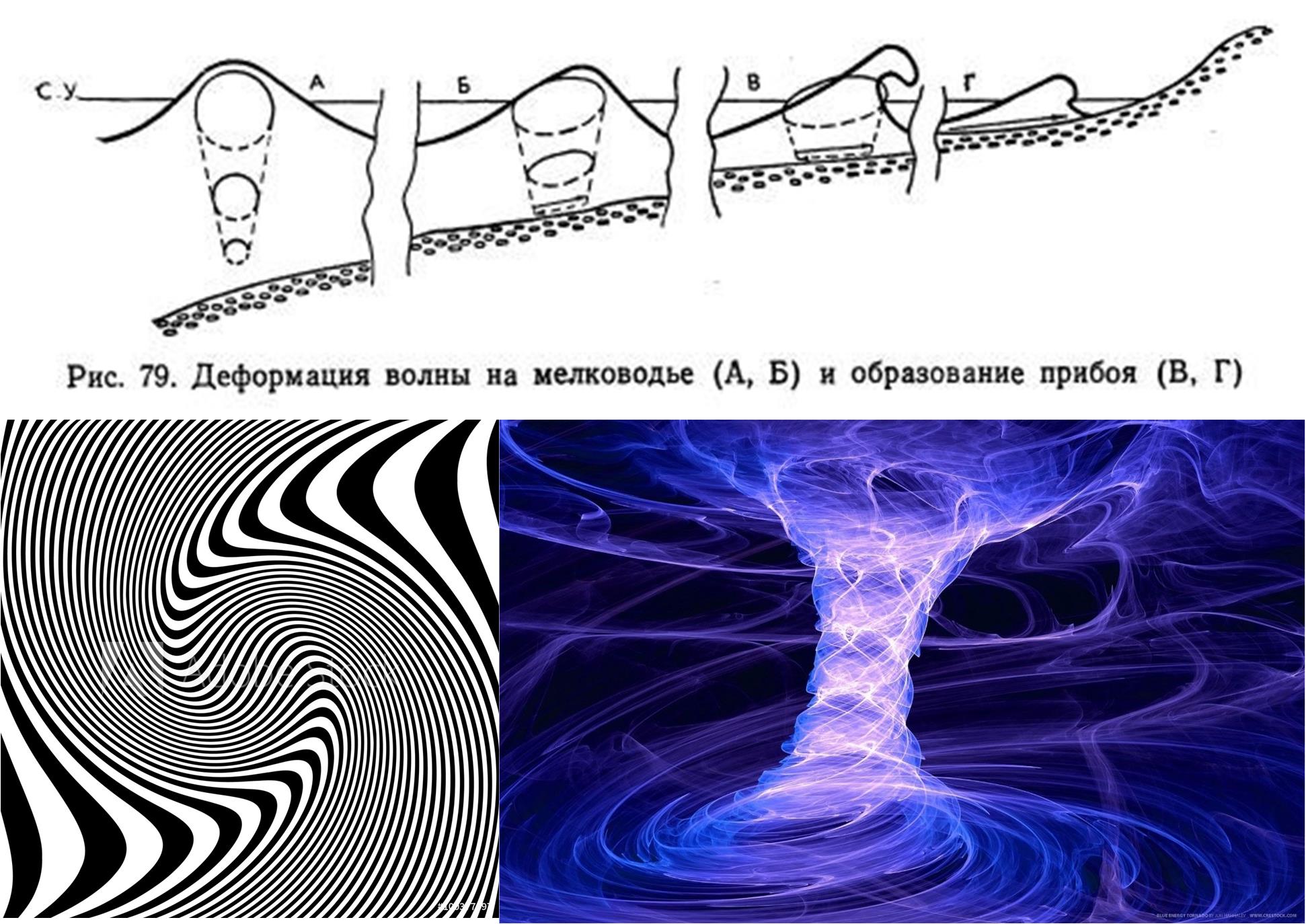Abb. 6. Der Mechanismus der Wellenverformung in Küstennähe und Beispiele für Prozesse, die bei Projektion auf einige Hyperebenen im lokalen Raum wie ein zufälliger Prozess aussehen können (Bilder aus dem Internet).

Im praktischen Teil werde ich die vorgeschlagenen Ansätze für die Arbeit mit weißem Rauschen zusammenfassen.

1. Fehlende Transitivitätseigenschaft bei zufälligen Prozessen.
2. Die Annahme, dass die Symmetrieeigenschaften in weißem Rauschen die Realisierung der Symmetrieeigenschaften von Prozessen sind, die höher sind als die Prozesse in der aktuell betrachteten Situation.
3. Lokalität zufälliger Prozesse. Diese Prämisse wird in der Publikation nicht explizit gezeigt, passt aber gut genug in den Rahmen der konstruktiven Mathematik. Sie alle verwenden es (konstruktive Mathematik), wenn Sie ein Skript schreiben, das die Anforderung festlegt, auf eine Speicherzelle zuzugreifen und deren Inhalt zu lesen. Da Sie standardmäßig meinen, dass in dieser Zelle ein bestimmter Wert 0 oder 1 vorhanden ist und nichts anderes vorhanden sein kann. Gutes Material, um sich mit ihren Ansätzen vertraut zu machen, wird hier vorgestellt: N.N. Nepeyvoda "Konstruktive Mathematik: Ein Überblick über Erfolge, Schwächen und Lektionen. Teil I " .

Praktischer Teil

Im ersten Teil wurde die Frage des Erds-Renyi-Theorems untersucht, die darin bestand, dass dieses Theorem nur in einer Quelle gefunden wurde, die aus dem Ungarischen übersetzt wurde. Dieses Buch wurde in der UdSSR veröffentlicht und es wurden keine Beweise oder Erwähnungen dafür gefunden . Infolge dieser Tatsache bestand im Allgemeinen eine Unsicherheit über seine Existenz und vor allem über seine Anwendung.

Als Ergebnis von Recherchen wurde es in der Arbeit von Filatov O.V. gefunden. „Ableitung von Formeln für die Postulate von Golomb. Eine Möglichkeit, eine Pseudozufallssequenz aus Mises-Frequenzen zu erstellen. Die Grundlagen der „Kombinatorik langer Sequenzen“ S. 15 Im Folgenden, Abbildung 7, zitiere ich das Original aus dem Material.


Abb. 7. Der Originalteil der Publikation Filatova OV „Ableitung von Formeln für die Postulate von Golomb. Eine Möglichkeit, eine Pseudozufallssequenz aus Mises-Frequenzen zu erstellen. Grundlagen der "Kombinatorik langer Sequenzen".

Der Satz von Erds-Renyi ist wie folgt formuliert:

Wenn Sie eine Münze N-mal werfen, fallen eine Reihe gleicher Seiten einer Münze in einer Reihe von Längen $$$\ log_2 {N}$beobachtet mit einer Wahrscheinlichkeit von 1, wobei N gegen unendlich tendiert.
Wir schreiben den Satz in den Formulierungen „Kombinatorik langer Sequenzen“ für eine Seite der Medaille:



Wir führen den Beweis durch:



Wie Sie sehen können, sind die Mises-Frequenzen für einen Zug, der aus einer Kette identischer Längensignale besteht $$$n = \ log_2 {N}$stimmen mit den Schlussfolgerungen des Erdos-Renyi-Theorems über die Wahrscheinlichkeit derselben Kette im Fall einer Zufallsreihe überein. So können Sie den Zweifel beseitigen und seine Existenz und die Möglichkeit der Anwendung erkennen.

Da die Veröffentlichung von Vermarktern bereits stärker empfohlen wurde, wird im nächsten Teil die Fortsetzung „Weißes Rauschen zeichnet ein schwarzes Quadrat. Teil 3. Anwendung. "

Andere Teile: Teil 1 , Teil 3 .