Im letzten Kapitel haben wir gelernt, dass tiefe neuronale Netze (GNSs) oft schwieriger zu trainieren sind als flache. Und das ist schlecht, denn wir haben allen Grund zu der Annahme, dass wenn wir die STS trainieren könnten, sie die Aufgaben viel besser erledigen könnten. Die Nachrichten aus dem vorherigen Kapitel sind zwar enttäuschend, werden uns aber nicht aufhalten. In diesem Kapitel werden wir Techniken entwickeln, mit denen wir tiefe Netzwerke trainieren und in die Praxis umsetzen können. Wir werden auch die Situation allgemeiner betrachten und uns kurz mit den jüngsten Fortschritten bei der Verwendung von GNS für die Bilderkennung, Sprache und für andere Anwendungen vertraut machen. Und überlegen Sie auch oberflächlich, welche Zukunft die neuronalen Netze und die KI erwarten können.
Dies wird ein langes Kapitel sein, also gehen wir etwas über das Inhaltsverzeichnis. Die Abschnitte sind nicht stark miteinander verbunden. Wenn Sie also einige grundlegende Konzepte zu neuronalen Netzen haben, können Sie mit dem Abschnitt beginnen, der Sie mehr interessiert.
Der Hauptteil des Kapitels ist eine Einführung in eine der beliebtesten Arten von tiefen Netzwerken: Deep Convolution Networks (GSS). Wir werden mit einem detaillierten Beispiel für die Verwendung eines Faltungsnetzwerks mit einem Code und anderen Dingen arbeiten, um das Problem der Klassifizierung handgeschriebener Ziffern aus dem MNIST-Datensatz zu lösen:
Wir beginnen unsere Überprüfung von Faltungsnetzwerken mit flachen Netzwerken, mit denen wir dieses Problem weiter oben in diesem Buch gelöst haben. In mehreren Schritten werden wir immer leistungsfähigere Netzwerke schaffen. Auf dem Weg werden wir viele leistungsstarke Technologien kennenlernen: Faltungen, Pooling, Verwendung von GPUs, um den Trainingsaufwand im Vergleich zu flachen Netzwerken erheblich zu erhöhen, algorithmische Erweiterung der Trainingsdaten (um Überanpassung zu reduzieren) mithilfe der Dropout-Technologie (auch um die Umschulung zu reduzieren), unter Verwendung von Ensembles von Netzwerken und anderen. Infolgedessen werden wir zu einem System kommen, dessen Fähigkeiten fast auf menschlicher Ebene liegen. Von den 10.000 MNIST-Überprüfungsbildern, die das System während des Trainings nicht gesehen hat, kann es 9967 korrekt erkennen. Und hier sind einige der Bilder, die nicht korrekt erkannt wurden. In der oberen rechten Ecke befinden sich die richtigen Optionen. Was unser Programm gezeigt hat, ist in der unteren rechten Ecke angegeben.
Viele von ihnen sind für Menschen schwer zu klassifizieren. Nehmen Sie zum Beispiel die dritte Ziffer in der obersten Zeile. Es scheint mir eher "9" als die offizielle Version von "8". Unser Netzwerk entschied auch, dass es "9" war. Zumindest können solche Fehler vollständig verstanden und vielleicht sogar genehmigt werden. Wir schließen unsere Diskussion über die Bilderkennung mit einem Überblick über die enormen Fortschritte, die das neuronale Netzwerk kürzlich erzielt hat (insbesondere Faltungsnetzwerke).
Der Rest des Kapitels widmet sich einer Diskussion über tiefes Lernen aus einer breiteren und weniger detaillierten Perspektive. Wir werden kurz auf andere NS-Modelle eingehen, insbesondere auf wiederkehrende NS und Einheiten des Langzeit-Kurzzeitgedächtnisses, und wie diese Modelle verwendet werden können, um Probleme bei der Spracherkennung, der Verarbeitung natürlicher Sprache und anderen zu lösen. Wir werden die Zukunft von NS und Zivilschutz diskutieren, von Ideen wie absichtsgesteuerten Benutzeroberflächen bis hin zur Rolle des tiefen Lernens in der KI.
Dieses Kapitel basiert auf Material aus früheren Kapiteln des Buches, in dem Ideen wie Backpropagation, Regularisierung, Softmax usw. verwendet und integriert werden. Um dieses Kapitel zu lesen, ist es jedoch nicht erforderlich, das Material aller vorherigen Kapitel zu erläutern. Es tut jedoch nicht weh,
Kapitel 1 zu lesen und die Grundlagen der Nationalversammlung kennenzulernen. Wenn ich die Konzepte aus den Kapiteln 2 bis 5 verwende, gebe ich bei Bedarf die erforderlichen Links zum Material.
Es ist erwähnenswert, dass dieses Kapitel dies nicht tut. Dies ist kein Schulungsmaterial zu den neuesten und coolsten Bibliotheken für die Arbeit mit NS. Wir werden STS nicht mit Dutzenden von Schichten trainieren, um Probleme auf dem neuesten Stand der Forschung zu lösen. Wir werden versuchen, einige der Grundprinzipien zu verstehen, die GNS zugrunde liegen, und sie auf den einfachen und leicht verständlichen Kontext von MNIST-Aufgaben anwenden. Mit anderen Worten, dieses Kapitel bringt Sie nicht an die Spitze der Region. Der Wunsch dieses und der vorhergehenden Kapitel ist es, sich auf die Grundlagen zu konzentrieren und Sie darauf vorzubereiten, eine breite Palette zeitgenössischer Werke zu verstehen.
Einführung in Faltungs-Neuronale Netze
In den vorherigen Kapiteln haben wir unseren neuronalen Netzen beigebracht, dass es ziemlich gut ist, Bilder von handgeschriebenen Zahlen zu erkennen:
Wir haben dazu Netzwerke verwendet, in denen benachbarte Schichten vollständig miteinander verbunden waren. Das heißt, jedes Neuron des Netzwerks wurde jedem Neuron der benachbarten Schicht zugeordnet:
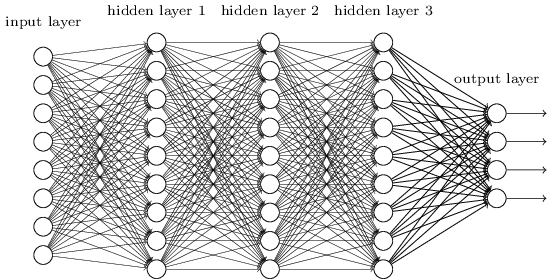
Insbesondere haben wir die Intensität jedes Pixels im Bild als Wert für das entsprechende Neuron der Eingangsschicht codiert. Für Bilder mit einer Größe von 28 x 28 Pixel bedeutet dies, dass das Netzwerk 784 (= 28 × 28) eingehende Neuronen hat. Dann haben wir die Gewichte und Offsets des Netzwerks so trainiert, dass die Ausgabe (es gab eine solche Hoffnung) das eingehende Bild korrekt identifizierte: '0', '1', '2', ..., '8' oder '9'.
Unsere frühen Netzwerke funktionieren ziemlich gut: Mit Trainings- und Testdaten aus den handgeschriebenen MNIST-Ziffern haben wir eine Klassifizierungsgenauigkeit von über 98% erreicht. Wenn Sie diese Situation jetzt bewerten, erscheint es seltsam, ein Netzwerk mit vollständig verbundenen Ebenen zur Klassifizierung von Bildern zu verwenden. Tatsache ist, dass ein solches Netzwerk die räumliche Struktur von Bildern nicht berücksichtigt. Beispielsweise gilt dies genau für Pixel, die weit voneinander entfernt sind, sowie für benachbarte Pixel. Es wird davon ausgegangen, dass Schlussfolgerungen zu solchen Konzepten der räumlichen Struktur auf der Grundlage der Untersuchung von Trainingsdaten gezogen werden sollten. Was aber, wenn wir, anstatt die Netzwerkstruktur von vorne zu beginnen, eine Architektur verwenden, die versucht, die räumliche Struktur zu nutzen? In diesem Abschnitt beschreibe ich Faltungs-Neuronale Netze (SNA). Sie verwenden eine spezielle Architektur, die sich besonders zur Klassifizierung von Bildern eignet. Durch die Verwendung einer solchen Architektur lernen SNAs schneller. Dies hilft uns dabei, tiefere und vielschichtigere Netzwerke zu trainieren, mit denen sich Bilder gut klassifizieren lassen. Heutzutage wird in den meisten Fällen der Bilderkennung Deep SNA oder eine ähnliche Variante verwendet.
Die Ursprünge der SNA reichen bis in die 1970er Jahre zurück. Die erste Arbeit, die ihre moderne Verbreitung begann, war die Arbeit von 1998, "
Gradient Learning for Recognizing Documents ". Lekun machte eine interessante
Bemerkung zur in der SNA verwendeten Terminologie: „Die Verbindung von Modellen wie Faltungsnetzwerken mit der Neurobiologie ist sehr oberflächlich. Deshalb nenne ich sie Faltungsnetzwerke, keine Faltungsnetzwerke, und deshalb nennen wir ihre Knotenelemente, nicht Neuronen. " Trotzdem verwendet die SNA viele Ideen aus der NS-Welt, die wir bereits untersucht haben: Rückausbreitung, Gradientenabstieg, Regularisierung, nichtlineare Aktivierungsfunktionen usw. Daher werden wir die allgemein akzeptierte Vereinbarung befolgen und sie als eine Art NA betrachten. Ich werde sie sowohl Netzwerke als auch neuronale Netzwerke und ihre Knoten nennen - sowohl Neuronen als auch Elemente.
SNA verwendet drei Grundideen: lokale Empfangsfelder, Gesamtgewichte und Pooling. Schauen wir uns diese Ideen der Reihe nach an.
Lokale Empfangsfelder
In vollständig verbundenen Netzwerkschichten werden Eingabeschichten durch vertikale Linien von Neuronen angezeigt. In der SNA ist es bequemer, die Eingabeschicht in Form eines Quadrats von Neuronen mit einer Dimension von 28 × 28 darzustellen, deren Werte den Pixelintensitäten des Bildes 28 × 28 entsprechen:
Wie üblich verknüpfen wir eingehende Pixel mit einer Schicht versteckter Neuronen. Wir werden jedoch nicht jedes Pixel mit jedem versteckten Neuron verknüpfen. Wir organisieren die Kommunikation in kleinen, lokalisierten Bereichen des eingehenden Bildes.
Genauer gesagt wird jedes Neuron der ersten verborgenen Schicht einem kleinen Teil eingehender Neuronen zugeordnet, beispielsweise einer 5 × 5-Region, die 25 eingehenden Pixeln entspricht. Für ein verstecktes Neuron sieht die Verbindung möglicherweise folgendermaßen aus:
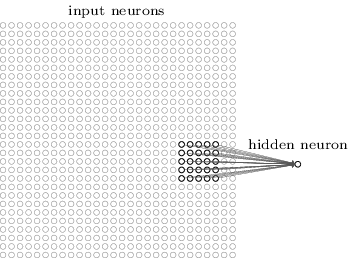
Dieser Teil des eingehenden Bildes wird als lokales Empfangsfeld für dieses versteckte Neuron bezeichnet. Dies ist ein kleines Fenster, in dem die eingehenden Pixel angezeigt werden. Jede Bindung lernt ihr Gewicht. Ein verstecktes Neuron untersucht auch die allgemeine Verschiebung. Wir können annehmen, dass dieses bestimmte Neuron lernt, sein spezifisches lokales Rezeptionsfeld zu analysieren.
Dann bewegen wir das lokale Empfangsfeld durch das eingehende Bild. Jedes lokale Empfangsfeld hat in der ersten verborgenen Schicht ein eigenes verstecktes Neuron. Beginnen Sie für eine genauere Darstellung mit dem lokalen Empfangsfeld in der oberen linken Ecke:
Bewegen Sie das lokale Empfangsfeld um ein Pixel nach rechts (ein Neuron), um es dem zweiten versteckten Neuron zuzuordnen:
Also bauen wir die erste versteckte Ebene. Beachten Sie, dass wenn unser eingehendes Bild 28x28 ist und das lokale Empfangsfeld 5x5 ist, sich 24x24 Neuronen in der verborgenen Schicht befinden. Dies liegt daran, dass wir das lokale Empfangsfeld nur um 23 Neuronen nach rechts (oder unten) bewegen können und dann auf die rechte (oder untere) Seite des eingehenden Bildes treffen.
In diesem Beispiel bewegen sich die lokalen Empfangsfelder jeweils um ein Pixel. Manchmal wird jedoch eine andere Schrittgröße verwendet. Zum Beispiel könnten wir das lokale Empfangsfeld um 2 Pixel zur Seite verschieben, und in diesem Fall können wir über die Größe von Schritt 2 sprechen. In diesem Kapitel werden wir hauptsächlich Schritt 1 verwenden, aber Sie sollten wissen, dass manchmal Experimente mit Schritten einer anderen Größe durchgeführt werden . Sie können mit der Schrittgröße wie mit anderen Hyperparametern experimentieren. Sie können auch die Größe des lokalen Empfangsfelds ändern, es stellt sich jedoch normalerweise heraus, dass eine größere Größe des lokalen Empfangsfelds bei Bildern, die deutlich größer als 28 x 28 Pixel sind, besser funktioniert.
Gesamtgewichte und Offsets
Ich erwähnte, dass jedes versteckte Neuron einen Versatz und 5x5 Gewichte hat, die mit seinem lokalen Empfangsfeld verbunden sind. Aber ich habe nicht erwähnt, dass wir für alle versteckten 24x24-Neuronen die gleichen Gewichte und Verschiebungen verwenden werden. Mit anderen Worten, für ein verstecktes Neuron j, k ist die Ausgabe gleich:
Hier ist σ die Aktivierungsfunktion, möglicherweise ein Sigmoid aus früheren Kapiteln. b ist der Gesamtversatzwert. w
l, m - Anordnung der Gesamtgewichte 5x5. Und schließlich bezeichnet a
x, y die Eingangsaktivierung an Position x, y.
Dies bedeutet, dass alle Neuronen in der ersten verborgenen Schicht dasselbe Zeichen erkennen, das sich nur in verschiedenen Teilen des Bildes befindet. Ein von einem versteckten Neuron erkanntes Zeichen ist eine bestimmte eingehende Sequenz, die zur Aktivierung eines Neurons führt: möglicherweise der Bildrand oder eine Form. Um zu verstehen, warum dies sinnvoll ist, nehmen wir an, dass unsere Gewichte und Verschiebungen so sind, dass ein verstecktes Neuron beispielsweise eine vertikale Fläche in einem bestimmten lokalen Empfangsfeld erkennen kann. Diese Fähigkeit ist wahrscheinlich an anderer Stelle im Bild nützlich. Daher ist es nützlich, denselben Merkmaldetektor über den gesamten Bildbereich zu verwenden. Noch abstrakter ist die SNA gut an die translatorische Invarianz von Bildern angepasst: Bewegen Sie beispielsweise das Bild der Katze ein wenig zur Seite, und es bleibt weiterhin das Bild der Katze. Richtig, die Bilder aus dem MNIST-Ziffernklassifizierungsproblem sind alle zentriert und in der Größe normalisiert. Daher hat MNIST eine geringere Translationsinvarianz als zufällige Bilder. Dennoch sind Merkmale wie Gesichter und Winkel wahrscheinlich auf der gesamten Oberfläche des eingehenden Bildes nützlich.
Aus diesem Grund wird die Zuordnung eines eingehenden Layers und eines verborgenen Layers manchmal als Feature-Map bezeichnet. Gewichte, die die Merkmalskarte definieren, nennen wir Gesamtgewichte. Und die Vorspannung, die die Merkmalskarte definiert, ist die allgemeine Vorspannung. Es wird oft gesagt, dass Gesamtgewichte und Verschiebung einen Kernel oder Filter bestimmen. Aber in der Literatur werden diese Begriffe manchmal aus einem etwas anderen Grund verwendet, und deshalb werde ich nicht weiter auf die Terminologie eingehen. Schauen wir uns besser einige konkrete Beispiele an.
Die von mir beschriebene Netzwerkstruktur kann nur ein lokalisiertes Attribut einer Art erkennen. Um Bilder zu erkennen, benötigen wir mehr Feature-Maps. Daher besteht die fertige Faltungsschicht aus mehreren verschiedenen Merkmalskarten:
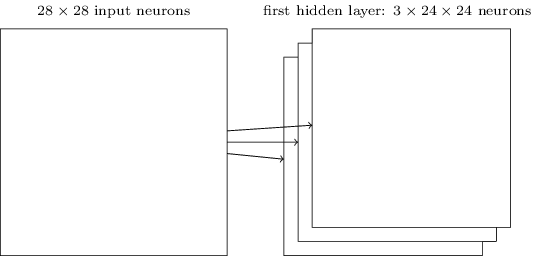
Das Beispiel zeigt 3 Feature-Maps. Jede Karte wird durch einen Satz von 5x5 Gesamtgewichten und einen gemeinsamen Versatz bestimmt. Infolgedessen kann ein solches Netzwerk drei verschiedene Arten von Zeichen erkennen, und jedes Zeichen kann in jedem Teil des Bildes gefunden werden.
Der Einfachheit halber habe ich drei Attributkarten gezogen. In der Praxis kann der SNA mehr (möglicherweise viel mehr) Feature-Maps verwenden. Einer der frühen SNSs, LeNet-5, verwendete 6 Feature-Karten, von denen jede einem 5x5-Empfangsfeld zugeordnet war, um MNIST-Ziffern zu erkennen. Daher ist das obige Beispiel LeNet-5 sehr ähnlich. In den Beispielen, die wir unabhängig voneinander weiterentwickeln werden, werden wir Faltungsschichten verwenden, die 20 und 40 Feature-Karten enthalten. Werfen wir einen kurzen Blick auf die Zeichen, die wir untersuchen werden:
Diese 20 Bilder entsprechen 20 verschiedenen Attributzuordnungen (Filter oder Kernel). Jede Karte wird durch ein 5x5-Bild dargestellt, das 5x5-Gewichten des lokalen Empfangsfeldes entspricht. Weiße Pixel bedeuten ein geringes (normalerweise negativeres) Gewicht, und die Feature-Map reagiert weniger auf die entsprechenden Pixel. Dunkle Pixel bedeuten mehr Gewicht und die Feature-Map reagiert stärker auf die entsprechenden Pixel. Grob gesagt zeigen diese Bilder die Zeichen, auf die die Faltungsschicht reagiert.
Welche Schlussfolgerungen können aus diesen Attributkarten gezogen werden? Die räumlichen Strukturen hier erschienen offensichtlich nicht zufällig - viele Zeichen zeigen klare helle und dunkle Bereiche. Dies deutet darauf hin, dass unser Netzwerk wirklich etwas in Bezug auf räumliche Strukturen lernt. Abgesehen davon ist es jedoch ziemlich schwierig zu verstehen, was diese Zeichen sind. Wir untersuchen offensichtlich keine
Gabor-Filter , die in vielen traditionellen Ansätzen zur Mustererkennung verwendet wurden. Tatsächlich wird jetzt viel Arbeit geleistet, um besser zu verstehen, welche Zeichen von der SNA genau untersucht werden. Wenn Sie interessiert sind, empfehle ich ab
2013 zu beginnen .
Der große Vorteil allgemeiner Gewichte und Offsets besteht darin, dass dadurch die Anzahl der für den SNA verfügbaren Parameter drastisch reduziert wird. Für jede Feature-Map benötigen wir 5 × 5 = 25 Gesamtgewichte und einen gemeinsamen Versatz. Daher sind für jede Feature-Map 26 Parameter erforderlich. Wenn wir 20 Feature-Maps haben, haben wir insgesamt 20 × 26 = 520 Parameter, die die Faltungsschicht definieren. Nehmen wir zum Vergleich an, wir haben eine vollständig verbundene erste Schicht mit 28 × 28 = 784 eingehenden Neuronen und relativ bescheidenen 30 versteckten Neuronen - wir haben dieses Schema in vielen Beispielen früher verwendet. Es ergeben sich 784 × 30 Gewichte plus 30 Offsets, insgesamt 23.550 Parameter. Mit anderen Worten, eine vollständig verbundene Schicht hat mehr als 40-mal mehr Parameter als eine Faltungsschicht.
Natürlich können wir die Anzahl der Parameter nicht direkt vergleichen, da sich diese beiden Modelle radikal unterscheiden. Intuitiv scheint es jedoch so zu sein, dass die Verwendung der Faltungs-Translationsinvarianz die Anzahl der Parameter verringert, die erforderlich sind, um eine Effizienz zu erzielen, die mit der eines vollständig verbundenen Modells vergleichbar ist. Dies wiederum wird das Training des Faltungsmodells beschleunigen und uns letztendlich helfen, mithilfe von Faltungsschichten tiefere Netzwerke aufzubauen.
Der Name "Faltung" stammt übrigens aus der Operation in Gleichung (125), die manchmal als
Faltung bezeichnet wird . Genauer gesagt, manchmal schreiben Menschen diese Gleichung als
1 = σ (b + w ∗ a
0 ), wobei eine
1 einen Satz von Ausgangsaktivierungen einer Merkmalskarte, eine
0 - einen Satz von Eingabeaktivierungen und * eine Faltungsoperation bezeichnet. Wir werden uns nicht eingehend mit der Mathematik der Windungen befassen, sodass Sie sich über diesen Zusammenhang nicht besonders Gedanken machen müssen. Es lohnt sich jedoch nur zu wissen, woher der Name stammt.
Schichten bündeln
Zusätzlich zu den in der SNA beschriebenen Faltungsschichten gibt es auch Pooling-Schichten. Sie werden normalerweise unmittelbar nach der Faltung verwendet. Sie sind bestrebt, Informationen aus der Ausgabe der Faltungsschicht zu vereinfachen.
Hier verwende ich den Ausdruck "Feature Map" nicht im Sinne der von der Faltungsschicht berechneten Funktion, sondern um die Aktivierung der Ausgabe von Neuronen der verborgenen Schicht anzuzeigen. Eine solche freie Verwendung von Begriffen findet sich häufig in der Forschungsliteratur.
Die Pooling-Schicht akzeptiert die Ausgabe jeder Faltungsschicht-Feature-Map und erstellt eine komprimierte Feature-Map. Beispielsweise kann jedes Element der Pooling-Schicht einen Abschnitt von beispielsweise 2 × 2 Neuronen der vorherigen Schicht zusammenfassen. Fallstudie: Ein gängiges Pooling-Verfahren ist das Max-Pooling. Beim maximalen Pooling gibt das Pooling-Element einfach die maximale Aktivierung aus dem 2x2-Abschnitt an, wie in der Abbildung gezeigt:
Da die Ausgabe von Faltungsschichtneuronen 24x24-Werte ergibt, erhalten wir nach dem Ziehen 12x12 Neuronen.Wie oben erwähnt, impliziert eine Faltungsschicht normalerweise etwas mehr als eine einzelne Merkmalskarte. Wir wenden das maximale Pooling auf jede Feature-Map einzeln an. Wenn wir also drei Feature-Maps haben, sehen die kombinierten Faltungs- und Max-Pooling-Ebenen folgendermaßen aus: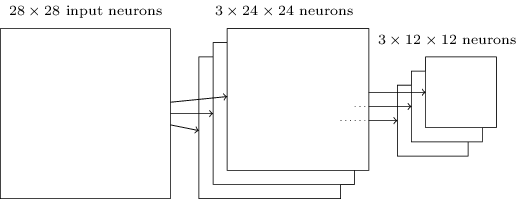
Max-Pulling kann als eine Möglichkeit des Netzwerks angesehen werden, zu fragen, ob sich an einer beliebigen Stelle des Bildes ein bestimmtes Zeichen befindet. Und dann verwirft sie Informationen über den genauen Standort. Es ist intuitiv klar, dass wenn ein Zeichen gefunden wird, seine genaue Position nicht mehr so wichtig ist wie seine ungefähre Position relativ zu anderen Zeichen. Der Vorteil besteht darin, dass die Anzahl der durch Pooling erhaltenen Features viel geringer ist, und dies hilft, die Anzahl der in den nächsten Schichten erforderlichen Parameter zu reduzieren.Max Pooling ist nicht die einzige Pooling-Technologie. Ein weiterer gängiger Ansatz ist das L2-Pooling. Anstatt die maximale Aktivierung der Region von 2x2-Neuronen zu nehmen, nehmen wir darin die Quadratwurzel der Summe der Quadrate der Aktivierung der 2x2-Region. Details der Ansätze unterscheiden sich, aber intuitiv ähnelt es dem Max-Pooling: L2-Pooling ist eine Möglichkeit, Informationen aus einer Faltungsschicht zu komprimieren. In der Praxis werden häufig beide Technologien eingesetzt. Manchmal verwenden Menschen andere Arten von Pooling. Wenn Sie Schwierigkeiten haben, die Qualität des Netzwerks zu optimieren, können Sie die unterstützenden Daten verwenden, um verschiedene Ansätze zum Ziehen zu vergleichen und den besten auszuwählen. Wir werden uns jedoch nicht um eine so detaillierte Optimierung kümmern.Zusammenfassend
Jetzt können wir alle Informationen zusammenführen und eine vollständige SNA erhalten. Es ähnelt der Architektur, die wir kürzlich überprüft haben, verfügt jedoch über eine zusätzliche Schicht von 10 Ausgangsneuronen, die 10 möglichen Werten der MNIST-Ziffern entsprechen ('0', '1', '2', ..):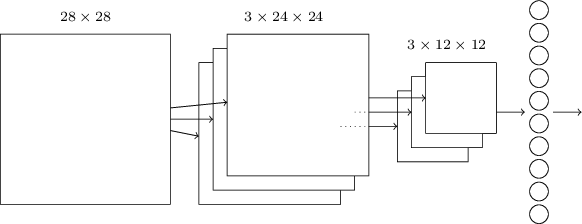
Das Netzwerk beginnt mit 28x28 verwendeten Eingangsneuronen um die Pixelintensität des MNIST-Bildes zu codieren. Danach folgt eine Faltungsschicht unter Verwendung der lokalen Empfangsfelder 5x5 und 3 Feature Maps. Das Ergebnis ist eine Schicht von Neuronen mit 3 x 24 x 24 versteckten Merkmalen. Der nächste Schritt ist eine maximale Pooling-Ebene, die auf 2x2 Bereiche auf jeder der drei Feature-Maps angewendet wird. Das Ergebnis ist eine Schicht von Neuronen mit 3 x 12 x 12 versteckten Merkmalen.Die letzte Verbindungsebene im Netzwerk ist vollständig verbunden. Das heißt, es verbindet jedes Neuron der Max-Pooling-Schicht mit jedem der 10 Ausgangsneuronen. Wir haben früher eine solche vollständig verbundene Architektur verwendet. Bitte beachten Sie, dass ich im obigen Diagramm der Einfachheit halber einen einzelnen Pfeil verwendet habe, der nicht alle Links anzeigt. Sie können sich alle leicht vorstellen.Diese Faltungsarchitektur unterscheidet sich sehr von dem, was wir zuvor verwendet haben. Das Gesamtbild ist jedoch ähnlich: Ein Netzwerk, das aus vielen einfachen Elementen besteht, deren Verhalten durch Gewichte und Offsets bestimmt wird. Das Ziel bleibt dasselbe: Verwenden Sie Trainingsdaten, um das Netzwerk in Gewichten und Offsets zu trainieren, damit das Netzwerk eingehende Nummern gut klassifiziert.Insbesondere werden wir wie in den vorherigen Kapiteln unser Netzwerk mit stochastischem Gradientenabstieg und Rückausbreitung trainieren. Der Vorgang läuft fast genauso ab wie zuvor. Wir müssen jedoch einige Änderungen am Backpropagation-Verfahren vornehmen. Tatsache ist, dass unsere Derivate für die Rückausbreitung für ein Netzwerk mit vollständig verbundenen Schichten gedacht waren. Glücklicherweise ist das Ändern von Ableitungen für Faltungs- und Max-Pooling-Schichten recht einfach. Wenn Sie die Details verstehen möchten, lade ich Sie ein, das folgende Problem zu lösen. Ich werde Sie warnen, dass es viel Zeit in Anspruch nehmen wird, es sei denn, Sie haben die frühen Fragen der Differenzierung der Rückausbreitung gründlich verstanden.Herausforderung
- . (BP1)-(BP4). , , - , . ?
Wir haben die Ideen hinter der SNA diskutiert. Lassen Sie uns sehen, wie sie in der Praxis funktionieren, indem einige SNAs implementiert und auf das MNIST-Problem der Ziffernklassifizierung angewendet werden. Wir werden das Programm network3.py verwenden, eine verbesserte Version der Programme network.py und network2.py, die in den vorherigen Kapiteln erstellt wurden. Das Programm network3.py verwendet Ideen aus der Dokumentation der Theano-Bibliothek (insbesondere der LeNet-5- Implementierung ) aus der Implementierung der Ausnahme von Misha Denil und Chris Olah . Der Programmcode ist auf GitHub verfügbar. Im nächsten Abschnitt werden wir den Code des Programms network3.py untersuchen und in diesem Abschnitt als Bibliothek zum Erstellen des SNA verwenden.Die Programme network.py und network2.py wurden unter Verwendung der Numpy-Matrixbibliothek in Python geschrieben. Sie arbeiteten auf der Grundlage erster Prinzipien und erreichten die detailliertesten Details der Rückausbreitung, des stochastischen Gradientenabfalls usw. Wenn wir diese Details verstehen, verwenden wir für network3.py die Theano-Bibliothek für maschinelles Lernen (siehe die wissenschaftliche Arbeit mit ihrer Beschreibung). Theano ist auch die Basis der beliebten Bibliotheken für NS Pylearn2 und Keras sowie Caffe und Torch .Die Verwendung von Theano erleichtert die Implementierung der Backpropagation in der SNA, da automatisch alle Karten gezählt werden. Theano ist auch deutlich schneller als unser vorheriger Code (der zum besseren Verständnis geschrieben wurde und nicht für Hochgeschwindigkeitsarbeiten). Daher ist es sinnvoll, ihn zum Trainieren komplexerer Netzwerke zu verwenden. Eine der großartigen Funktionen von Theano besteht insbesondere darin, Code sowohl auf der CPU als auch auf der GPU auszuführen, sofern verfügbar. Das Ausführen auf einer GPU erhöht die Geschwindigkeit erheblich und hilft beim Trainieren komplexerer Netzwerke.Um parallel zum Buch zu arbeiten, müssen Sie Theano auf Ihrem System installieren. Befolgen Sie dazu die Anweisungen auf der Projekthomepage. Zum Zeitpunkt des Schreibens und Startens der Beispiele war Theano 0.7 verfügbar. Ich habe einige Experimente unter Mac OS X Yosemite ohne GPU durchgeführt. Einige unter Ubuntu 14.04 mit einer NVIDIA-GPU. Und einige sind da und da. Setzen Sie zum Starten von network3.py das GPU-Flag im Code auf True oder False. Darüber hinaus können die folgenden Anweisungen Ihnen helfen, Theano auf Ihrer GPU auszuführen . Es ist auch einfach, Schulungsunterlagen online zu finden. Wenn Sie keine eigene GPU haben, können Sie sich an Amazon Web Services EC2 G2 wenden. Aber selbst mit einer GPU funktioniert unser Code nicht sehr schnell. Viele Experimente dauern einige Minuten bis mehrere Stunden. Die komplexesten auf einer einzelnen CPU werden mehrere Tage lang ausgeführt. Wie in den vorherigen Kapiteln empfehle ich, das Experiment zu starten und weiterzulesen, wobei die Funktionsweise regelmäßig überprüft wird. Ohne Verwendung einer GPU empfehle ich, die Anzahl der Trainingszeiten für die komplexesten Experimente zu reduzieren.Um grundlegende Vergleichsergebnisse zu erhalten, beginnen wir mit einer flachen Architektur mit einer verborgenen Schicht, die 100 verborgene Neuronen enthält. Wir werden 60 Epochen studieren, die Lerngeschwindigkeit η = 0,1 verwenden, die Größe des Minipakets beträgt 10 und wir werden ohne Regularisierung lernen.In diesem Abschnitt habe ich eine bestimmte Anzahl von Trainingsperioden festgelegt. Ich mache dies aus Gründen der Klarheit im Lernprozess. In der Praxis ist es nützlich, frühe Stopps zu verwenden, die Genauigkeit des Bestätigungssatzes zu verfolgen und das Training zu beenden, wenn wir davon überzeugt sind, dass sich die Genauigkeit der Bestätigung nicht mehr verbessert:>>> import network3 >>> from network3 import Network >>> from network3 import ConvPoolLayer, FullyConnectedLayer, SoftmaxLayer >>> training_data, validation_data, test_data = network3.load_data_shared() >>> mini_batch_size = 10 >>> net = Network([ FullyConnectedLayer(n_in=784, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)
Die beste Klassifizierungsgenauigkeit betrug 97,80%. Dies ist die Klassifizierungsgenauigkeit test_data, geschätzt aus dem Trainingszeitalter, in der wir die beste Klassifizierungsgenauigkeit für Daten aus validation_data erhalten haben. Durch die Verwendung validierender Daten zur Entscheidung über die Genauigkeitsbewertung kann eine Umschulung vermieden werden. Dann werden wir es tun. Ihre Ergebnisse können geringfügig variieren, da Netzwerkgewichte und Offsets zufällig initialisiert werden.
Die Genauigkeit von 97,80% liegt ziemlich nahe an der Genauigkeit von 98,04%, die in Kapitel 3 unter Verwendung einer ähnlichen Netzwerkarchitektur und Trainingshyperparametern erhalten wurde. Insbesondere verwenden beide Beispiele flache Netzwerke mit einer verborgenen Schicht, die 100 verborgene Neuronen enthält. Beide Netzwerke lernen 60 Epochen mit einer Minipaketgröße von 10 und einer Lernrate von η = 0,1.
Im früheren Netzwerk gab es jedoch zwei Unterschiede. Zunächst führten wir eine Regularisierung durch, um die Auswirkungen der Umschulung zu verringern. Durch die Regularisierung des aktuellen Netzwerks wird die Genauigkeit verbessert, jedoch nicht wesentlich. Daher werden wir vorerst nicht darüber nachdenken. Zweitens, obwohl die letzte Schicht des frühen Netzwerks Sigmoid-Aktivierungen und die Cross-Entropy-Kostenfunktion verwendete, verwendet das aktuelle Netzwerk die letzte Schicht mit Softmax und die logarithmische Wahrscheinlichkeitsfunktion als Kostenfunktion. Wie in Kapitel 3 beschrieben, ist dies keine wesentliche Änderung. Ich habe aus irgendeinem Grund nicht von einem zum anderen gewechselt - hauptsächlich, weil Softmax und die logarithmische Wahrscheinlichkeitsfunktion in modernen Netzwerken häufiger zur Klassifizierung von Bildern verwendet werden.
Können wir die Ergebnisse mithilfe einer tieferen Netzwerkarchitektur verbessern?
Beginnen wir mit dem Einfügen einer Faltungsschicht ganz am Anfang des Netzwerks. Wir werden das lokale Empfangsfeld 5x5 verwenden, eine Schrittlänge von 1 und 20 Feature-Karten. Wir werden auch eine maximale Pooling-Ebene einfügen, die Funktionen mithilfe von 2x2-Pooling-Fenstern kombiniert. Die gesamte Netzwerkarchitektur sieht also ähnlich aus wie im vorherigen Abschnitt, jedoch mit einer zusätzlichen vollständig verbundenen Schicht:
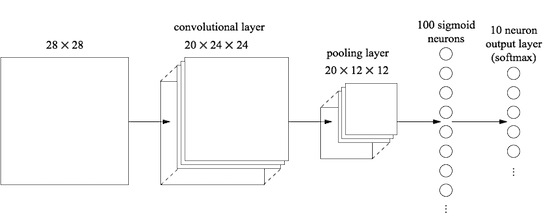
In dieser Architektur werden die Faltungs- und Pooling-Schichten in der lokalen räumlichen Struktur trainiert, die im eingehenden Trainingsbild enthalten ist, und die letzte vollständig verbundene Schicht wird auf einer abstrakteren Ebene trainiert, wobei globale Informationen aus dem gesamten Bild integriert werden. Dies ist ein häufig verwendetes Schema in der SNA.
Lassen Sie uns ein solches Netzwerk trainieren und sehen, wie es sich verhält.
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2)), FullyConnectedLayer(n_in=20*12*12, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)
Wir erhalten eine Genauigkeit von 98,78%, was deutlich über den vorherigen Ergebnissen liegt. Wir haben den Fehler um mehr als ein Drittel reduziert - ein hervorragendes Ergebnis.
Bei der Beschreibung der Netzwerkstruktur betrachtete ich Faltungs- und Pooling-Schichten als eine einzige Schicht. Betrachten Sie sie als separate Schichten oder als einzelne Schicht - eine Frage der Präferenz. network3.py betrachtet sie als eine Ebene, da der Code auf diese Weise kompakter ist. Es ist jedoch einfach, network3.py so zu ändern, dass die Ebenen einzeln festgelegt werden können.
Übung
- Welche Klassifizierungsgenauigkeit erhalten wir, wenn wir die vollständig verbundene Schicht absenken und nur die Faltungs- / Poolschicht und die Softmax-Schicht verwenden? Hilft die Aufnahme einer vollständig verbundenen Schicht?
Können wir das Ergebnis um 98,78% verbessern?
Versuchen wir, die zweite Faltungs- / Pooling-Schicht einzufügen. Wir werden es zwischen der vorhandenen Faltung / Pooling und den vollständig verbundenen verborgenen Schichten einfügen. Wir verwenden wieder das lokale 5x5-Empfangsfeld und den Pool in 2x2-Abschnitten. Mal sehen, was passiert, wenn wir ein Netzwerk mit ungefähr den gleichen Hyperparametern wie zuvor trainieren:
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2)), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2)), FullyConnectedLayer(n_in=40*4*4, n_out=100), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.1, validation_data, test_data)
Und wieder haben wir eine Verbesserung: Jetzt erhalten wir eine Genauigkeit von 99,06%!
Im Moment stellen sich zwei natürliche Fragen. Erstens: Was bedeutet es, die zweite Faltungs- / Pooling-Schicht zu verwenden? Sie können davon ausgehen, dass auf der zweiten Faltungs- / Pooling-Ebene "12 x 12" -Bilder zur Eingabe gelangen, deren "Pixel" das Vorhandensein (oder Fehlen) bestimmter lokalisierter Merkmale im eingehenden Originalbild darstellen. Das heißt, wir können davon ausgehen, dass eine bestimmte Version des eingehenden Originalbilds zur Eingabe dieser Ebene gelangt. Dies wird eine abstraktere und prägnantere Version sein, hat aber immer noch genügend räumliche Struktur, so dass es sinnvoll ist, eine zweite Faltungs- / Ziehschicht zu verwenden, um sie zu verarbeiten.
Eine angenehme Sichtweise, die jedoch eine zweite Frage aufwirft. Bei der Ausgabe von der vorherigen Schicht werden 20 separate KPs erhalten, daher kommen 20 × 12 × 12 Gruppen von Eingabedaten zur zweiten Faltungs- / Pooling-Schicht. Es stellt sich heraus, dass in der Faltungs- / Pooling-Schicht 20 separate Bilder enthalten sind und nicht ein Bild, wie dies bei der ersten Faltungs- / Pooling-Ebene der Fall war. Wie müssen Neuronen aus der zweiten Faltungs- / Poolschicht auf viele dieser eingehenden Bilder reagieren? Tatsächlich erlauben wir einfach, dass jedes Neuron dieser Schicht auf der Basis aller 20x5x5 Neuronen trainiert wird, die in sein lokales Empfangsfeld eintreten. In weniger formalen Begriffen haben Merkmaldetektoren in der zweiten Faltungs- / Poolschicht Zugriff auf alle Merkmale der ersten Schicht, jedoch nur innerhalb ihrer spezifischen lokalen Empfangsfelder.
Ein solches Problem wäre übrigens in der ersten Schicht aufgetreten, wenn die Bilder farbig wären. In diesem Fall hätten wir 3 Eingabeattribute für jedes Pixel, die den roten, grünen und blauen Kanälen des Originalbilds entsprechen. Und dann würden wir auch Zeichendetektoren Zugriff auf alle Farbinformationen gewähren, jedoch nur im Rahmen ihres lokalen Empfangsfeldes.
Herausforderung
- Verwendung der Aktivierungsfunktion in Form einer hyperbolischen Tangente. Zu Beginn dieses Buches erwähnte ich mehrmals Beweise dafür, dass die Tanh-Funktion, eine hyperbolische Tangente, möglicherweise besser als Aktivierungsfunktion als als Sigmoid geeignet ist. Wir haben nichts damit gemacht, da wir mit dem Sigmoid gute Fortschritte gemacht haben. Aber versuchen wir einige Experimente mit Tanh als Aktivierungsfunktion. Versuchen Sie, ein Tang-aktiviertes Netzwerk mit Faltungsschichten und vollständig verbundenen Ebenen zu trainieren (Sie können activity_fn = tanh als Parameter an die Klassen ConvPoolLayer und FullyConnectedLayer übergeben). Beginnen Sie mit denselben Hyperparametern wie das Sigmoid-Netzwerk, trainieren Sie jedoch das Netzwerk aus 20 Epochen, nicht aus 60. Wie verhält sich das Netzwerk? Was wird passieren, wenn wir bis zur 60. Ära weitermachen? Versuchen Sie, ein Diagramm über die Genauigkeit der Bestätigung der Arbeit durch Epochen für Tangente und Sigmoid bis zur 60. Ära zu erstellen. Wenn Ihre Ergebnisse meinen ähnlich sind, werden Sie feststellen, dass das tangentiale Netzwerk etwas schneller lernt, die resultierende Genauigkeit beider Netzwerke jedoch gleich ist. Können Sie erklären, warum dies passiert? Ist es möglich, mit einem Sigmoid die gleiche Lerngeschwindigkeit zu erreichen - zum Beispiel durch Ändern der Lerngeschwindigkeit oder durch Skalieren (denken Sie daran, dass σ (z) = (1 + tanh (z / 2)) / 2)? Probieren Sie fünf oder sechs verschiedene Hyperparameter oder Netzwerkarchitekturen aus und suchen Sie, wo die Tangente vor dem Sigmoid liegen kann. Ich stelle fest, dass diese Aufgabe offen ist. Persönlich habe ich beim Umschalten auf die Tangente keine ernsthaften Vorteile festgestellt, obwohl ich keine umfassenden Experimente durchgeführt habe, und vielleicht werden Sie sie finden. In jedem Fall werden wir bald einen Vorteil beim Umschalten auf eine begradigte lineare Aktivierungsfunktion finden, so dass wir uns nicht mehr mit dem Thema hyperbolischer Tangente befassen werden.
Mit geraden linearen Elementen
Das Netzwerk, das wir derzeit entwickelt haben, ist eine der Netzwerkoptionen, die in der
fruchtbaren Arbeit von 1998 verwendet wurden , in der die Aufgabe von MNIST, einem Netzwerk namens LeNet-5, erstmals vorgestellt wurde. Dies ist eine gute Grundlage für weitere Experimente, um das Verständnis des Problems und der Intuition zu verbessern. Insbesondere gibt es viele Möglichkeiten, wie wir unser Netzwerk ändern können, um die Ergebnisse zu verbessern.
Lassen Sie uns zunächst unsere Neuronen so ändern, dass wir anstelle der Sigmoid-Aktivierungsfunktion begradigte lineare Elemente (ReLU) verwenden können. Das heißt, wir werden die Aktivierungsfunktion der Form f (z) ≡ max (0, z) verwenden. Wir werden ein Netzwerk von 60 Epochen mit einer Geschwindigkeit von η = 0,03 trainieren. Ich fand auch, dass es etwas bequemer ist, die L2-Regularisierung mit dem Regularisierungsparameter λ = 0,1 zu verwenden:
>>> from network3 import ReLU >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1)
Ich habe eine Klassifizierungsgenauigkeit von 99,23%. Eine bescheidene Verbesserung gegenüber Sigmoid-Ergebnissen (99,06%). In all meinen Experimenten stellte ich jedoch fest, dass Netzwerke, die auf ReLU basieren, Netzwerken voraus sind, die auf der Sigmoid-Aktivierungsfunktion mit beneidenswerter Konstanz basieren. Anscheinend bietet der Wechsel zu ReLU echte Vorteile, um dieses Problem zu lösen.
Was macht die ReLU-Aktivierungsfunktion besser als die Sigmoid- oder hyperbolische Tangente? Im Moment verstehen wir das nicht besonders. Es wird normalerweise gesagt, dass die Funktion max (0, z) im Gegensatz zu Sigmoid-Neuronen bei großem z nicht gesättigt ist, und dies hilft ReLU-Neuronen, weiter zu lernen. Ich argumentiere nicht, aber diese Rechtfertigung kann nicht als umfassend bezeichnet werden, sondern ist nur eine Art Beobachtung (ich erinnere Sie daran, dass wir in
Kapitel 2 über die Sättigung gesprochen haben).
ReLU wurde in den letzten Jahren aktiv eingesetzt. Sie wurden aus empirischen Gründen übernommen: Einige Leute versuchten es mit ReLU, oft einfach aufgrund von Vermutungen oder heuristischen Argumenten. Sie haben gute Ergebnisse erzielt und die Praxis hat sich verbreitet. In einer idealen Welt hätten wir eine Theorie, die uns sagt, welche Anwendungen welche Aktivierungsfunktionen für welche Anwendungen am besten sind. Aber vorerst haben wir noch einen langen Weg vor uns. Es wird mich überhaupt nicht wundern, wenn durch die Auswahl einer noch geeigneteren Aktivierungsfunktion weitere Verbesserungen im Betrieb der Netzwerke erzielt werden können. Ich erwarte auch, dass in den kommenden Jahrzehnten eine gute Theorie der Aktivierungsfunktionen entwickelt wird. Aber heute müssen wir uns auf schlecht studierte Faust- und Erfahrungsregeln verlassen.
Erweiterung der Trainingsdaten
Eine andere Möglichkeit, die uns möglicherweise dabei helfen kann, unsere Ergebnisse zu verbessern, besteht darin, die Trainingsdaten algorithmisch zu erweitern. Der einfachste Weg, die Trainingsdaten zu erweitern, besteht darin, jedes Trainingsbild um ein Pixel nach oben, unten, rechts oder links zu verschieben. Dies kann durch Ausführen des Programms
expand_mnist.py erfolgen .
$ python expand_mnist.py
Mit dem Start des Programms werden 50.000 Trainingsbilder von MNIST in einen erweiterten Satz von 250.000 Trainingsbildern umgewandelt. Dann können wir diese Trainingsbilder verwenden, um das Netzwerk zu trainieren. Wir werden das gleiche Netzwerk wie zuvor mit ReLU verwenden. In meinen ersten Experimenten habe ich die Anzahl der Trainingsperioden reduziert - es war sinnvoll, weil wir fünfmal mehr Trainingsdaten haben. Durch die Erweiterung des Datensatzes wurde jedoch der Effekt der Umschulung erheblich reduziert. Daher kehrte ich nach mehreren Experimenten zur Anzahl der Epochen 60 zurück. Lassen Sie uns auf jeden Fall trainieren:
>>> expanded_training_data, _, _ = network3.load_data_shared( "../data/mnist_expanded.pkl.gz") >>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1)
Mit fortgeschrittenen Trainingsdaten erhielt ich eine Genauigkeit von 99,37%. Eine solche fast triviale Änderung führt zu einer signifikanten Verbesserung der Klassifizierungsgenauigkeit. Und wie bereits erwähnt, kann die algorithmische Datenerweiterung weiterentwickelt werden. Zur Erinnerung: 2003 haben
Simard, Steinkraus und Platt die Genauigkeit ihres Netzwerks auf 99,6% verbessert. Ihr Netzwerk war unserem ähnlich, sie verwendeten zwei Faltungs- / Poolschichten, gefolgt von einer vollständig verbundenen Schicht mit 100 Neuronen. Die Details ihrer Architektur waren unterschiedlich - sie hatten beispielsweise keine Gelegenheit, ReLU zu nutzen -, aber der Schlüssel zur Verbesserung der Arbeitsqualität war die Erweiterung der Schulungsdaten. Dies wurde erreicht, indem MNIST-Trainingsbilder gedreht, übertragen und verzerrt wurden. Sie entwickelten auch den Prozess der „elastischen Verzerrung“, bei dem die zufälligen Vibrationen der Armmuskeln beim Schreiben nachgeahmt werden. Durch die Kombination all dieser Prozesse haben sie das effektive Volumen ihrer Trainingsdatenbank erheblich erhöht und dadurch eine Genauigkeit von 99,6% erreicht.
Herausforderung
- Die Idee von Faltungsschichten besteht darin, unabhängig von der Position im Bild zu arbeiten. Aber dann mag es seltsam erscheinen, dass unser Netzwerk besser trainiert ist, wenn wir einfach Eingabebilder verschieben. Können Sie erklären, warum dies eigentlich ganz vernünftig ist?
Hinzufügen einer zusätzlichen vollständig verbundenen Ebene
Ist es möglich, die Situation zu verbessern? Eine Möglichkeit besteht darin, genau das gleiche Verfahren anzuwenden, aber gleichzeitig die Größe der vollständig verbundenen Schicht zu erhöhen. Ich habe das Programm mit 300 und 1000 Neuronen ausgeführt und Ergebnisse in 99,46% bzw. 99,43% erzielt. Dies ist interessant, aber nicht besonders überzeugend als das vorherige Ergebnis (99,37%).
Was ist mit dem Hinzufügen einer zusätzlichen vollständig verbundenen Ebene? Versuchen wir, eine zusätzliche vollständig verbundene Schicht hinzuzufügen, sodass wir zwei versteckte vollständig verbundene Schichten mit 100 Neuronen haben:
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer(n_in=40*4*4, n_out=100, activation_fn=ReLU), FullyConnectedLayer(n_in=100, n_out=100, activation_fn=ReLU), SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size) >>> net.SGD(expanded_training_data, 60, mini_batch_size, 0.03, validation_data, test_data, lmbda=0.1)
Somit erreichte ich eine Verifizierungsgenauigkeit von 99,43%. Das erweiterte Netzwerk hat die Leistung erneut nicht wesentlich verbessert. Nachdem ich ähnliche Experimente mit vollständig verbundenen Schichten von 300 und 100 Neuronen durchgeführt hatte, erhielt ich eine Genauigkeit von 99,48% und 99,47%. Inspirierend, aber nicht wie ein echter Gewinn.
Was ist los? Ist es möglich, dass erweiterte oder zusätzliche vollständig verbundene Schichten nicht zur Lösung des MNIST-Problems beitragen? Oder kann unser Netzwerk besser abschneiden, aber wir entwickeln es in die falsche Richtung? Vielleicht könnten wir zum Beispiel eine strengere Regularisierung verwenden, um die Umschulung zu reduzieren. Eine Möglichkeit ist die in Kapitel 3 erwähnte Dropout-Technik. Denken Sie daran, dass die Grundidee des Ausschlusses darin besteht, einzelne Aktivierungen beim Training des Netzwerks zufällig zu entfernen. Infolgedessen wird das Modell widerstandsfähiger gegen den Verlust einzelner Beweise, und daher ist es weniger wahrscheinlich, dass es sich auf einige kleine nicht standardmäßige Merkmale der Trainingsdaten stützt. Versuchen wir, die Ausnahme auf die letzte vollständig verbundene Ebene anzuwenden:
>>> net = Network([ ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2), activation_fn=ReLU), ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12), filter_shape=(40, 20, 5, 5), poolsize=(2, 2), activation_fn=ReLU), FullyConnectedLayer( n_in=40*4*4, n_out=1000, activation_fn=ReLU, p_dropout=0.5), FullyConnectedLayer( n_in=1000, n_out=1000, activation_fn=ReLU, p_dropout=0.5), SoftmaxLayer(n_in=1000, n_out=10, p_dropout=0.5)], mini_batch_size) >>> net.SGD(expanded_training_data, 40, mini_batch_size, 0.03, validation_data, test_data)
Mit diesem Ansatz erreichen wir eine Genauigkeit von 99,60%, was viel besser ist als die vorherigen, insbesondere unsere grundlegende Einschätzung - ein Netzwerk mit 100 versteckten Neuronen, das eine Genauigkeit von 99,37% ergibt.
Zwei Änderungen sind hier erwähnenswert.
Zuerst habe ich die Anzahl der Trainingszeiten auf 40 reduziert: Ausnahme reduziert die Umschulung und wir lernen schneller.
Zweitens enthalten vollständig verbundene verborgene Schichten 1000 Neuronen und nicht wie zuvor 100. Natürlich eliminiert die Ausnahme tatsächlich viele Neuronen während des Trainings, daher sollten wir eine Art Expansion erwarten. Tatsächlich führte ich Experimente mit 300 und 1000 Neuronen durch und erhielt bei 1000 Neuronen eine etwas bessere Bestätigung.
Verwenden von Network Ensemble
Eine einfache Möglichkeit, die Effizienz zu verbessern, besteht darin, mehrere neuronale Netze zu erstellen und sie dann dazu zu bringen, für eine bessere Klassifizierung zu stimmen. Nehmen wir zum Beispiel an, wir haben 5 verschiedene NS nach dem obigen Rezept trainiert und jeder von ihnen hat eine Genauigkeit von nahezu 99,6% erreicht. Obwohl alle Netzwerke eine ähnliche Genauigkeit aufweisen, können sie aufgrund unterschiedlicher zufälliger Initialisierung unterschiedliche Fehler aufweisen. Es ist anzunehmen, dass bei einer Abstimmung mit 5 NA ihre allgemeine Klassifizierung besser ist als die eines separaten Netzwerks.
Es klingt zu schön, um wahr zu sein, aber das Zusammenstellen solcher Ensembles ist ein üblicher Trick sowohl für die Nationalversammlung als auch für andere MO-Techniken. Und es gibt tatsächlich eine Verbesserung der Effizienz: Wir erhalten eine Genauigkeit von 99,67%. Mit anderen Worten, unser Netzwerkensemble klassifiziert alle 10.000 Verifizierungsbilder mit Ausnahme von 33 korrekt.
Die verbleibenden Fehler sind unten aufgeführt. Das Etikett in der oberen rechten Ecke ist die korrekte Klassifizierung gemäß MNIST-Daten, und in der unteren rechten Ecke ist das Etikett, das vom Netzwerkensemble empfangen wurde:
Es lohnt sich, sich mit den Bildern zu befassen. Die ersten beiden Ziffern 6 und 5 sind die wirklichen Fehler unseres Ensembles. Sie können jedoch verstanden werden, ein solcher Fehler könnte vom Menschen gemacht werden. Diese 6 ist 0 sehr ähnlich, und 5 ist 3 sehr ähnlich. Das dritte Bild, angeblich 8, sieht wirklich eher wie 9 aus. Ich stehe auf der Seite des Netzwerkensembles: Ich denke, dass er die Arbeit besser gemacht hat als die Person, die diese Figur geschrieben hat. Andererseits wird das vierte Bild, 6, von Netzwerken wirklich falsch klassifiziert.
Usw. In den meisten Fällen erscheint die Netzwerklösung plausibel, und in einigen Fällen wurde die Zahl besser klassifiziert als von der Person, die sie geschrieben hat. Insgesamt weisen unsere Netzwerke eine außergewöhnliche Effizienz auf, insbesondere wenn wir uns daran erinnern, dass sie 9967 Bilder korrekt klassifiziert haben, die wir hier nicht präsentieren.
In diesem Zusammenhang können mehrere offensichtliche Fehler verstanden werden. Sogar eine vorsichtige Person irrt sich manchmal. Daher kann ich nur von einer äußerst genauen und methodischen Person ein besseres Ergebnis erwarten. Unser Netzwerk nähert sich der menschlichen Leistung.Warum haben wir die Ausnahme nur auf vollständig verbundene Ebenen angewendet?
Wenn Sie sich den obigen Code genau ansehen, werden Sie feststellen, dass wir die Ausnahme nur auf vollständig verbundene Netzwerkschichten angewendet haben, nicht jedoch auf Faltungsschichten. Im Prinzip kann ein ähnliches Verfahren auf Faltungsschichten angewendet werden. Dies ist jedoch nicht erforderlich: Faltungsschichten weisen einen erheblichen Widerstand gegen Umschulungen auf. Dies liegt daran, dass die Faltungsfilter durch die Gesamtgewichte gleichzeitig über das gesamte Bild lernen. Infolgedessen ist es weniger wahrscheinlich, dass sie über einige lokale Verzerrungen in den Trainingsdaten stolpern. Daher besteht keine besondere Notwendigkeit, andere Regularisierer auf sie anzuwenden, wie z. B. Ausnahmen.Weitermachen
Sie können die Effizienz der Lösung des MNIST-Problems noch weiter verbessern. Rodrigo Benenson stellte eine informative Tafel zusammen, die den Fortschritt im Laufe der Jahre und Links zur Arbeit zeigt. Viele der Werke verwenden GSS ähnlich wie wir. Wenn Sie in Ihrer Arbeit stöbern, werden Sie viele interessante Techniken finden, und Sie können einige davon implementieren. In diesem Fall ist es ratsam, die Implementierung mit einem einfachen Netzwerk zu beginnen, das schnell trainiert werden kann. Auf diese Weise können Sie schnell verstehen, was passiert.Zum größten Teil werde ich nicht versuchen, die jüngsten Arbeiten zu überprüfen. Aber ich kann einer Ausnahme nicht widerstehen. Es geht um eine Arbeit im Jahr 2010. Ich mag ihre Einfachheit in ihr. Das Netzwerk ist mehrschichtig und verwendet nur vollständig verbundene Schichten (ohne Windungen). In ihrem erfolgreichsten Netzwerk gibt es versteckte Schichten mit 2500, 2000, 1500, 1000 bzw. 500 Neuronen. Sie verwendeten ähnliche Ideen, um Trainingsdaten zu erweitern. Abgesehen davon wendeten sie einige weitere Tricks an, einschließlich des Fehlens von Faltungsschichten: Es war das einfachste Vanille-Netzwerk, das mit der richtigen Geduld und der Verfügbarkeit geeigneter Computerfähigkeiten bereits in den 1980er Jahren hätte unterrichtet werden können (wenn das MNIST-Set damals existiert hätte). Sie erreichten eine Klassifizierungsgenauigkeit von 99,65%, was in etwa unserer entspricht. Die Hauptsache in ihrer Arbeit ist die Verwendung eines sehr großen und tiefen Netzwerks und die Verwendung von GPUs zur Beschleunigung des Lernens. Dadurch konnten sie viele Epochen lernen. Sie nutzten auch die langen Trainingsintervalle,und schrittweise die Lerngeschwindigkeit von 10 reduziert-3 bis 10 -6 . Der Versuch, mit einer Architektur wie der ihren ähnliche Ergebnisse zu erzielen, ist eine interessante Übung.Warum lernen wir?
Im vorigen Kapitel haben wir grundlegende Hindernisse für das Erlernen von Deep Multilayer NS gesehen. Insbesondere haben wir gesehen, dass der Gradient sehr instabil wird: Beim Übergang von der Ausgangsschicht zur vorherigen neigt der Gradient dazu, entweder zu verschwinden (das Problem des verschwindenden Gradienten) oder explosives Wachstum (das Problem des explosiven Gradientenwachstums). Da der Gradient das Signal ist, das wir für das Training verwenden, verursacht dies Probleme.Wie haben wir es geschafft, sie zu vermeiden?Die Antwort lautet natürlich: Wir konnten sie nicht vermeiden. Stattdessen haben wir einige Dinge getan, die es uns trotzdem ermöglichten, weiterzuarbeiten. Insbesondere: (1) die Verwendung von Faltungsschichten reduziert die Anzahl der darin enthaltenen Parameter erheblich, was das Lernproblem erheblich erleichtert; (2) die Verwendung effizienterer Regularisierungstechniken (Ausschluss- und Faltungsschichten); (3) Verwendung von ReLU anstelle von Sigmoidneuronen zur Beschleunigung des Lernens - empirisch bis zu 3-5 mal; (4) die Verwendung der GPU und die Fähigkeit, im Laufe der Zeit zu lernen. Insbesondere haben wir in jüngsten Experimenten 40 Epochen mit einem Datensatz untersucht, der fünfmal größer ist als die Standard-MNIST-Trainingsdaten. Zu Beginn des Buches haben wir hauptsächlich 30 Epochen mit Standard-Trainingsdaten untersucht. Die Kombination der Faktoren (3) und (4) ergibt einen solchen Effekt,als ob wir 30 mal länger als zuvor studiert hätten.Sie sagen wahrscheinlich: "Ist das alles?" Ist das alles, was man braucht, um tiefe neuronale Netze zu trainieren? Und wegen was hat dann die Aufregung Feuer gefangen? “Natürlich haben wir andere Ideen verwendet: ausreichend große Datensätze (um Umschulungen zu vermeiden); korrekte Kostenfunktion (um Lernverlangsamungen zu vermeiden); gute Initialisierung der Gewichte (auch um eine Verlangsamung des Lernens aufgrund der Sättigung der Neuronen zu vermeiden); algorithmische Erweiterung des Trainingsdatensatzes. Wir haben diese und andere Ideen in früheren Kapiteln besprochen und hatten normalerweise die Möglichkeit, sie mit kleinen Notizen in diesem Kapitel wiederzuverwenden.Nach allen Angaben ist dies ein ziemlich einfacher Satz von Ideen. Einfach, aber in der Lage, viel zu tun, wenn es in einem Komplex verwendet wird. Es stellte sich heraus, dass der Einstieg in das tiefe Lernen ziemlich einfach war!?
Wenn wir Faltungs- / Pooling-Schichten als eine betrachten, gibt es in unserer endgültigen Architektur 4 versteckte Schichten. Hat ein solches Netzwerk einen tiefen Titel verdient? Natürlich sind 4 versteckte Schichten viel mehr als in flachen Netzwerken, die wir zuvor untersucht haben. Die meisten Netzwerke hatten eine verborgene Schicht, manchmal 2. Auf der anderen Seite haben moderne fortgeschrittene Netzwerke manchmal Dutzende von verborgenen Schichten. Manchmal habe ich Leute getroffen, die dachten, je tiefer das Netzwerk, desto besser. Wenn Sie nicht genügend versteckte Ebenen verwenden, bedeutet dies, dass Sie nicht wirklich tief lernen. Ich denke nicht, insbesondere weil ein solcher Ansatz die Definition von Deep Learning in ein Verfahren verwandelt, das von momentanen Ergebnissen abhängt. Ein echter Durchbruch in diesem Bereich war die Idee der Praktikabilität, über Netzwerke mit einer oder zwei verborgenen Schichten hinauszugehen.Mitte der 2000er Jahre vorherrschend. Dies war ein echter Durchbruch und eröffnete ein Forschungsfeld mit ausdrucksstärkeren Modellen. Nun, eine bestimmte Anzahl von Schichten ist nicht von grundlegendem Interesse. Die Verwendung tiefer Netzwerke ist ein Werkzeug, um andere Ziele zu erreichen, beispielsweise die Verbesserung der Klassifizierungsgenauigkeit.Verfahrensfrage
In diesem Abschnitt haben wir reibungslos von flachen Netzwerken mit einer verborgenen Schicht zu mehrschichtigen Faltungsnetzwerken gewechselt. Alles schien so einfach! Wir haben eine Änderung vorgenommen und eine Verbesserung erhalten. Wenn Sie anfangen zu experimentieren, garantiere ich, dass normalerweise nicht alles so reibungslos verläuft. Ich habe Ihnen eine gekämmte Geschichte vorgestellt, in der viele Experimente weggelassen wurden, auch erfolglose. Ich hoffe, dass diese gekämmte Geschichte Ihnen hilft, die Grundideen besser zu verstehen. Er riskiert jedoch, einen unvollständigen Eindruck zu vermitteln. Um ein gutes, funktionierendes Netzwerk zu erhalten, ist viel Versuch und Irrtum erforderlich, durchsetzt mit Frustration. In der Praxis können Sie mit einer Vielzahl von Experimenten rechnen. Um den Prozess zu beschleunigen, können Ihnen die Informationen in Kapitel 3 zur Auswahl der Netzwerkhyperparameter sowie die dort erwähnte zusätzliche Literatur helfen.Code für unsere Faltungsnetzwerke
Okay, schauen wir uns jetzt den Code für unser Programm network3.py an. Strukturell ähnelt es network2.py, das wir in Kapitel 3 entwickelt haben, aber die Details unterscheiden sich aufgrund der Verwendung der Theano-Bibliothek. Beginnen wir mit der FullyConnectedLayer-Klasse, ähnlich den zuvor untersuchten Ebenen. class FullyConnectedLayer(object): def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0): self.n_in = n_in self.n_out = n_out self.activation_fn = activation_fn self.p_dropout = p_dropout
Der Großteil der __init__ -Methode spricht für sich selbst, aber ein paar Hinweise können helfen, den Code zu verdeutlichen. Wie üblich initialisieren wir Gewichte und Offsets zufällig mit normalen Zufallswerten mit geeigneten Standardabweichungen. Diese Zeilen sehen etwas unverständlich aus. Der größte Teil des seltsamen Codes lädt jedoch Gewichte und Offsets in das, was die Theano-Bibliothek als gemeinsam genutzte Variablen bezeichnet. Dadurch wird sichergestellt, dass Variablen auf der GPU verarbeitet werden können, sofern verfügbar. Wir werden uns nicht mit diesem Thema befassen - wenn Sie interessiert sind, lesen Sie die Dokumentation für Theano. Beachten Sie auch, dass diese Initialisierung von Gewichten und Offsets für die Sigmoid-Aktivierungsfunktion gilt. Idealerweise würden wir für Funktionen wie hyperbolische Tangente und ReLU Gewichte und Offsets unterschiedlich initialisieren. Dieses Problem wird in zukünftigen Aufgaben behandelt.Die Methode __init__ endet mit der Anweisung self.params = [self.w, self.b]. Dies ist eine bequeme Möglichkeit, alle mit einer Ebene verbundenen Lernparameter zusammenzuführen. Network.SGD verwendet später die params-Attribute, um herauszufinden, welche Variablen in der Network-Klasseninstanz trainiert werden können.Die set_inpt-Methode wird verwendet, um Eingaben an eine Ebene zu übergeben und die entsprechende Ausgabe zu berechnen. Ich schreibe inpt anstelle von Eingabe, da Eingabe eine integrierte Python-Funktion ist. Wenn Sie mit ihnen spielen, kann dies zu unvorhersehbarem Programmverhalten und schwer zu diagnostizierenden Fehlern führen. Tatsächlich übergeben wir Eingaben auf zwei Arten: über self.inpt und self.inpt_dropout. Dies geschieht, da wir während des Trainings möglicherweise Ausnahmen verwenden möchten. Und dann müssen wir einen Teil der self.p_dropout-Neuronen entfernen. Dies ist, was die Funktion dropout_layer in der vorletzten Zeile der Methode set_inpt tut. Self.inpt_dropout und self.output_dropout werden also während des Trainings verwendet, und self.inpt und self.output werden für alle anderen Zwecke verwendet, z. B. zur Bewertung der Genauigkeit von Validierungs- und Testdaten.Die Klassendefinitionen für ConvPoolLayer und SoftmaxLayer ähneln FullyConnectedLayer. So ähnlich, dass ich den Code nicht einmal zitiere. Wenn Sie interessiert sind, können Sie den vollständigen Code des Programms später in diesem Kapitel lesen.Es ist erwähnenswert, einige verschiedene Details zu erwähnen. In ConvPoolLayer und SoftmaxLayer berechnen wir die Ausgabeaktivierungen natürlich so, dass sie dem Layertyp entsprechen. Glücklicherweise ist Theano einfach zu handhaben und verfügt über integrierte Operationen zur Berechnung der Faltung, des Max-Pooling und der Softmax-Funktion.Es ist weniger offensichtlich, wie Gewichte und Offsets in der Softmax-Ebene initialisiert werden - wir haben dies nicht diskutiert. Wir haben erwähnt, dass es für sigmoidale Gewichtsschichten notwendig ist, entsprechend parametrisierte normale Zufallsverteilungen zu initialisieren. Dieses heuristische Argument galt jedoch für Sigmoid-Neuronen (und mit geringfügigen Korrekturen für Tang-Neuronen). Es gibt jedoch keinen besonderen Grund für dieses Argument, auf Softmax-Ebenen anzuwenden. Daher gibt es keinen Grund, diese Initialisierung von vornherein erneut anzuwenden. Stattdessen initialisiere ich alle Gewichte und Offsets auf 0. Die Option ist spontan, funktioniert aber in der Praxis ziemlich gut.Wir haben also alle Schichtenklassen untersucht. Was ist mit der Netzwerkklasse? Beginnen wir mit der __init__ -Methode: class Network(object): def __init__(self, layers, mini_batch_size): """ layers, , mini_batch_size """ self.layers = layers self.mini_batch_size = mini_batch_size self.params = [param for layer in self.layers for param in layer.params] self.x = T.matrix("x") self.y = T.ivector("y") init_layer = self.layers[0] init_layer.set_inpt(self.x, self.x, self.mini_batch_size) for j in xrange(1, len(self.layers)): prev_layer, layer = self.layers[j-1], self.layers[j] layer.set_inpt( prev_layer.output, prev_layer.output_dropout, self.mini_batch_size) self.output = self.layers[-1].output self.output_dropout = self.layers[-1].output_dropout
Der größte Teil des Codes spricht für sich. Die Zeile self.params = [Parameter für Ebene in ...] sammelt alle Parameter für jede Ebene in einer einzigen Liste. Wie bereits vorgeschlagen, verwendet die Network.SGD-Methode self.params, um herauszufinden, aus welchen Parametern das Netzwerk lernen kann. Die Linien self.x = T.matrix ("x") und self.y = T.ivector ("y") definieren die symbolischen Variablen Theano x und y. Sie repräsentieren die Eingabe und die gewünschte Ausgabe des Netzwerks.Dies ist kein Tutorial zur Verwendung von Theano, daher werde ich nicht auf die Bedeutung symbolischer Variablen eingehen (siehe Dokumentation und auch eines der Tutorials)) Grob gesagt bezeichnen sie mathematische Variablen, keine spezifischen. Mit ihnen können Sie viele normale Operationen ausführen: Addieren, Subtrahieren, Multiplizieren, Anwenden von Funktionen usw. Theano bietet viele Möglichkeiten, solche symbolischen Variablen zu manipulieren, zu falten, maximal zu ziehen und so weiter. Die Hauptsache ist jedoch die Möglichkeit einer schnellen symbolischen Differenzierung unter Verwendung einer sehr allgemeinen Form des Backpropagation-Algorithmus. Dies ist äußerst nützlich, um einen stochastischen Gradientenabstieg auf eine Vielzahl von Netzwerkarchitekturen anzuwenden. Insbesondere definieren die folgenden Codezeilen die symbolische Ausgabe des Netzwerks. Wir beginnen mit der Zuordnung der Eingabe zur ersten Ebene: init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
Die Eingabedaten werden jeweils einzeln übertragen, daher wird dort ihre Größe angegeben. Wir übergeben die Eingabe von self.x zweimal: Tatsache ist, dass wir das Netzwerk auf zwei verschiedene Arten verwenden können (mit oder ohne Ausnahme). Die for-Schleife verbreitet die symbolische Variable self.x durch die Netzwerkschichten. Auf diese Weise können wir die endgültigen Attribute output und output_dropout definieren, die symbolisch die Ausgabe des Netzwerks darstellen.Nachdem wir uns mit der Initialisierung des Netzwerks befasst haben, schauen wir uns dessen Training mit der SGD-Methode an. Der Code sieht lang aus, ist aber recht einfach aufgebaut. Erklärungen folgen dem Code: def SGD(self, training_data, epochs, mini_batch_size, eta, validation_data, test_data, lmbda=0.0): """ - .""" training_x, training_y = training_data validation_x, validation_y = validation_data test_x, test_y = test_data
Die ersten Zeilen sind klar, sie unterteilen die Datensätze in die Komponenten x und y und berechnen die Anzahl der in jedem Datensatz verwendeten Minipakete. Die folgenden Zeilen sind interessanter und zeigen, warum es so interessant ist, mit der Theano-Bibliothek zu arbeiten. Ich werde sie hier zitieren:
In diesen Zeilen definieren wir symbolisch die regulierte Kostenfunktion basierend auf der logarithmischen Wahrscheinlichkeitsfunktion, berechnen die entsprechenden Ableitungen in der Gradientenfunktion und auch die entsprechenden Parameteraktualisierungen. Mit Theano können wir dies alles in wenigen Zeilen erledigen. Das einzige, was verborgen bleibt, ist, dass bei der Berechnung der Kosten die Kostenmethode für die Ausgabeschicht aufgerufen wird. Dieser Code befindet sich an anderer Stelle in network3.py. Aber es ist kurz und einfach. Mit der Definition all dessen ist alles bereit, die Funktion train_mb zu definieren, die symbolische Theano-Funktion, die Aktualisierungen verwendet, um Netzwerkparameter durch Minipaketindex zu aktualisieren. In ähnlicher Weise berechnen die Funktionen validate_mb_accuracy und test_mb_accuracy die Netzwerkgenauigkeit für ein bestimmtes Minipaket von Validierungs- oder Verifizierungsdaten. Mittelung über diese Funktionen,Wir können die Genauigkeit für die gesamten Validierungs- und Verifizierungsdatensätze berechnen.Der Rest der SGD-Methode spricht für sich selbst - wir gehen einfach nacheinander durch die Epochen, trainieren das Netzwerk immer wieder anhand von Minipaketen mit Trainingsdaten und berechnen die Genauigkeit der Bestätigung und Überprüfung.Jetzt verstehen wir die wichtigsten Teile des Jahres network3.py. Lassen Sie uns kurz das gesamte Programm durchgehen. Es ist nicht notwendig, alles im Detail zu studieren, aber Sie möchten vielleicht über die Maßen gehen und sich vielleicht mit einigen besonders beliebten Passagen befassen. Aber der beste Weg, das Programm zu verstehen, besteht natürlich darin, es zu ändern, etwas Neues hinzuzufügen und die Teile zu überarbeiten, die Ihrer Meinung nach verbessert werden können. Nach dem Code stelle ich einige Aufgaben vor, die eine Reihe von ersten Vorschlägen enthalten, was hier getan werden kann. Hier ist der Code. """network3.py ~~~~~~~~~~~~~~ Theano . (, , -, softmax) (, , ReLU; ). CPU , network.py network2.py. , , GPU, . Theano, network.py network2.py. , . , API network2.py. , , . , , . Theano (http://deeplearning.net/tutorial/lenet.html ), (https://github.com/mdenil/dropout ) (http://colah.imtqy.com ). Theano 0.6 0.7, . """
Die Aufgaben
- SGD . , . network3.py , .
- Network , .
- SGD , η ( , , , ).
- , . network3.py, . , , . .
- .
- – . , , , ? .
- ReLU , ( -) . . , ReLU ( ). , c>0 c L−1 , L – . , softmax? ReLU? ? , , . , ReLU.
- . , ReLU? , ? : «» . – , - - .