Diskrete Mathematik für WMS: Clustering von Lagerbeständen

Der Artikel beschreibt, wie wir bei der Einführung eines WMS- Systems mit der Notwendigkeit konfrontiert wurden, ein nicht standardmäßiges Clustering-Problem zu lösen, und mit welchen Algorithmen wir es gelöst haben. Wir werden Ihnen erklären, wie wir einen systematischen, wissenschaftlichen Ansatz zur Lösung des Problems angewendet haben, auf welche Schwierigkeiten wir gestoßen sind und welche Lehren wir gezogen haben.

Diese Veröffentlichung beginnt mit einer Reihe von Artikeln, in denen wir unsere erfolgreichen Erfahrungen bei der Implementierung von Optimierungsalgorithmen in Lagerprozessen teilen. Ziel der Artikelserie ist es, das Publikum mit den Aufgaben zur Optimierung des Lagerbetriebs in nahezu jedem mittleren und großen Lager vertraut zu machen und über unsere Erfahrungen bei der Lösung solcher Probleme und die dabei auftretenden Fallstricke zu berichten. Die Artikel sind nützlich für diejenigen, die in der Lagerlogistikbranche arbeiten, WMS- Systeme implementieren, sowie für Programmierer, die sich für mathematische Anwendungen in der Geschäfts- und Prozessoptimierung im Unternehmen interessieren.

Prozessengpass

2018 haben wir ein Projekt zur Einführung eines WMS- Systems im Lager des Unternehmens LD Trading House in Tscheljabinsk durchgeführt. Einführung des Produkts „1C-Logistics: Warehouse Management 3“ für 20 Jobs: WMS- Betreiber, Ladenbesitzer, Gabelstaplerfahrer. Das Lager hat durchschnittlich ca. 4.000 m2, die Anzahl der Zellen beträgt 5000 und die Anzahl der SKU 4500. Die Kugelhähne unserer eigenen Produktion in verschiedenen Größen von 1 kg bis 400 kg werden im Lager gelagert. Die Lagerbestände im Lager werden im Rahmen von Chargen gelagert, da die Waren gemäß FIFO und den „Inline“ -Spezifikationen der Produktplatzierung ausgewählt werden müssen (Erläuterung unten).

Bei der Entwicklung von Automatisierungsschemata für Lagerprozesse waren wir mit dem bestehenden Problem der nicht optimalen Lagerung von Lagerbeständen konfrontiert. Das Stapeln und Lagern von Kranen weist, wie bereits erwähnt, „Reihen“ -Spezifikationen auf. Das heißt, die Produkte in der Zelle sind in Reihen übereinander gestapelt, und die Fähigkeit, ein Stück auf ein Stück zu legen, fehlt häufig (sie fallen einfach und das Gewicht ist nicht gering). Aus diesem Grund stellt sich heraus, dass sich nur eine Nomenklatur einer Charge in einer Stücklagereinheit befinden kann.

Die Produkte kommen täglich im Lager an und jede Ankunft ist eine separate Charge. Insgesamt werden nach einem Monat Lagerbetrieb 30 separate Lose erstellt, obwohl jedes in einer separaten Zelle gelagert werden sollte. Die Waren werden oft nicht in ganzen Paletten, sondern in Stücken ausgewählt. Infolgedessen wird im Bereich der Stückauswahl in vielen Zellen das folgende Bild beobachtet: In einer Zelle mit einem Volumen von mehr als 1 m3 befinden sich mehrere Kranstücke, die weniger als 5-10% des Zellvolumens einnehmen (siehe Abb. 1) )

Abb. 1. Foto mehrerer Warenstücke in einer Zelle

Angesichts der suboptimalen Nutzung der Speicherkapazität. Um mir das Ausmaß der Katastrophe vorzustellen, kann ich Zahlen anführen: Im Durchschnitt gibt es zwischen 100 und 300 Zellen solcher Zellen mit einem spärlichen Rest in verschiedenen Perioden des Lagerbetriebs. Da das Lager relativ klein ist, wird dieser Faktor in den Ladezeiten des Lagers zu einem „engen Hals“ und hemmt die Lagerprozesse erheblich.

Idee, ein Problem zu lösen

Die Idee kam auf: die Chargen von Rückständen mit den nächstgelegenen Daten zu einer einzelnen Charge zu bringen und solche Waagen mit einer einheitlichen Charge kompakt in einer Zelle oder in mehreren zu platzieren, wenn in einer nicht genügend Platz vorhanden ist, um die Gesamtzahl der Waagen aufzunehmen.


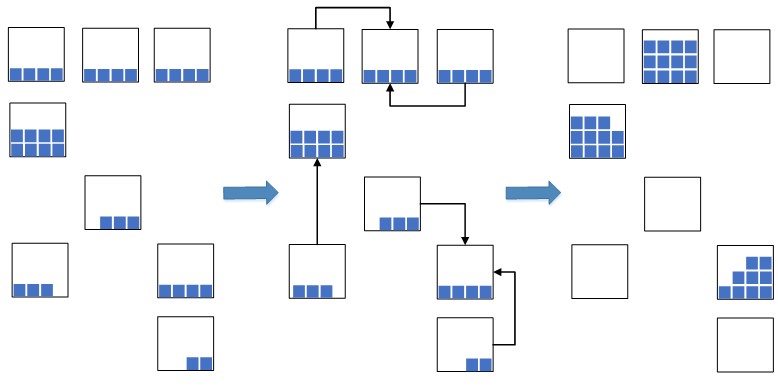Abb. 2. Zellkomprimierungsschema

Auf diese Weise können Sie den belegten Lagerraum, der für die neu platzierten Waren verwendet wird, erheblich reduzieren. In einer Situation mit Überlastung der Lagerkapazitäten ist eine solche Maßnahme äußerst notwendig, andernfalls ist möglicherweise nicht genügend freier Platz für die Platzierung neuer Waren vorhanden, was zu einem Stopp der Lager- und Nachfüllprozesse im Lager führt. Zuvor wurde vor der Implementierung des WMS- Systems eine solche Operation manuell durchgeführt, was nicht effektiv war, da der Prozess des Findens geeigneter Rückstände in den Zellen ziemlich lang war. Mit der Einführung von WMS-Systemen beschlossen sie nun, den Prozess zu automatisieren, zu beschleunigen und intelligent zu machen.

Der Prozess zur Lösung dieses Problems ist in zwei Phasen unterteilt:

• In der ersten Phase finden wir Gruppen von Parteien, deren Datum für die Komprimierung geschlossen ist.
• In der zweiten Stufe berechnen wir für jede Gruppe von Chargen die kompakteste Platzierung von Produktresten in Zellen.

Im aktuellen Artikel konzentrieren wir uns auf die erste Stufe des Algorithmus und belassen die Abdeckung der zweiten Stufe für den nächsten Artikel.

Suchen Sie nach einem mathematischen Modell eines Problems

Bevor wir uns hinsetzen, um Code zu schreiben und unser Fahrrad zu erfinden, haben wir uns entschlossen, dieses Problem wissenschaftlich anzugehen: mathematisch zu formulieren, es auf das bekannte diskrete Optimierungsproblem zu reduzieren und effektive vorhandene Algorithmen zu verwenden, um es zu lösen, oder diese vorhandenen Algorithmen als Grundlage zu nehmen und sie zu modifizieren unter den Besonderheiten der zu lösenden praktischen Aufgabe.

Da sich aus der Geschäftserklärung des Problems eindeutig ergibt, dass es sich um Mengen handelt, formulieren wir ein solches Problem in Bezug auf die Mengenlehre.

Lass $$$P$ - die Menge aller Lose der Reste einiger Waren auf Lager. Lass $$$C$ - die angegebene Konstante von Tagen. Lass $$$K$ - eine Teilmenge von Chargen, bei der die Datumsdifferenz für alle Chargenpaare der Teilmenge die Konstante nicht überschreitet $$$C$ . Finden Sie die Mindestanzahl disjunkter Teilmengen $$$K$ so dass alle Teilmengen $$$K$ gemeinsam würde viel geben $$$P$ .

Darüber hinaus müssen wir nicht nur die Mindestanzahl von Teilmengen finden, sondern auch, damit solche Teilmengen so groß wie möglich sind. Dies liegt an der Tatsache, dass wir nach dem Clustering von Chargen die Reste der in den Zellen gefundenen Chargen „komprimieren“. Lassen Sie uns anhand eines Beispiels veranschaulichen. Angenommen, auf der Zeitachse sind viele Parteien verteilt, wie in Abbildung 3 dargestellt.
Abb. 3. Mehrere Partitionierungsoptionen

Von den beiden Optionen zum Aufteilen der Menge P mit der gleichen Anzahl von Teilmengen ist die erste Partition (a) für unsere Aufgabe am vorteilhaftesten. Denn je mehr Parteien in Gruppen sind, desto mehr Komprimierungskombinationen erscheinen und desto wahrscheinlicher ist es, die kompakteste Komprimierung zu finden. Natürlich ist eine solche Regel nichts anderes als eine Heuristik und unsere spekulative Annahme. Obwohl, wie ein Computerexperiment gezeigt hat, unter Berücksichtigung einer solchen Maximierungsbedingung die Kompaktheit der nachfolgenden Kompression der Rückstände im Durchschnitt 5–10% höher ist als die Kompression, die ohne Berücksichtigung einer solchen Bedingung erstellt wurde.

Mit anderen Worten, kurz gesagt, wir müssen Gruppen oder Cluster ähnlicher Parteien finden, bei denen das Ähnlichkeitskriterium durch eine Konstante bestimmt wird $$$C$ . Diese Aufgabe erinnert uns an das bekannte Clustering-Problem. Es ist wichtig zu sagen, dass sich das betrachtete Problem vom Clustering-Problem darin unterscheidet, dass es in unserem Problem eine streng definierte Bedingung für das Kriterium der Ähnlichkeit von Cluster-Elementen gibt, die durch die Konstante bestimmt wird $$$C$ und im Clustering-Problem gibt es keine solche Bedingung. Die Erklärung des Clustering-Problems und Informationen zu dieser Aufgabe finden Sie hier.

Wir haben es also geschafft, das Problem zu formulieren und das klassische Problem mit einer ähnlichen Formulierung zu finden. Jetzt müssen Sie bekannte Algorithmen in Betracht ziehen, um das Problem zu lösen, um das Rad nicht neu zu erfinden, sondern die Best Practices zu übernehmen und anzuwenden. Um das Clustering-Problem zu lösen, haben wir die beliebtesten Algorithmen betrachtet, nämlich: $$$k$ -mittel $$$c$ -Mittel, Algorithmus zur Auswahl verbundener Komponenten, minimaler Spanning Tree-Algorithmus. Eine Beschreibung und Analyse solcher Algorithmen finden Sie hier.

Um unser Problem zu lösen, Clustering-Algorithmen $$$k$ -mittel und $$$c$ -Mittel sind überhaupt nicht anwendbar, da die Anzahl der Cluster nie vorher bekannt ist $$$k$ und solche Algorithmen berücksichtigen nicht die Beschränkung der Konstante von Tagen. Solche Algorithmen wurden zunächst verworfen.
Um unser Problem zu lösen, sind der Algorithmus zur Auswahl verbundener Komponenten und der Minimum-Spanning-Tree-Algorithmus besser geeignet, aber wie sich herausstellte, können sie nicht direkt auf das zu lösende Problem angewendet werden, um eine gute Lösung zu erhalten. Um dies zu verdeutlichen, betrachten wir die Logik der Funktionsweise solcher Algorithmen, wie sie auf unser Problem angewendet werden.

Betrachten Sie die Grafik $$$G$ in denen die Tops viele Partys sind $$$P$ und die Kante zwischen den Eckpunkten $$$p_1$ und $$$p_2$ hat ein Gewicht, das der Differenz der Tage zwischen den Chargen entspricht $$$p_1$ und $$$p_2$ . Im Algorithmus zur Auswahl verbundener Komponenten wird ein Eingabeparameter angegeben $$$R$ wo $$$R \ leq C$ und in der Grafik $$$G$ Alle Kanten, für die Gewicht entfernt wird, werden entfernt $$$R$ . Es bleiben nur die nächsten Objektpaare verbunden. Die Bedeutung des Algorithmus besteht darin, einen solchen Wert auszuwählen $$$R$ , in dem der Graph in mehrere verbundene Komponenten „zerfällt“, wobei die zu diesen Komponenten gehörenden Parteien unser durch die Konstante bestimmtes Ähnlichkeitskriterium erfüllen $$$C$ . Die resultierenden Komponenten sind Cluster.

Der Minimum-Spanning-Tree-Algorithmus baut zunächst auf einem Diagramm auf $$$G$ Minimaler Spanning Tree, und entfernt dann nacheinander die Kanten mit dem größten Gewicht, bis der Graph in mehrere verbundene Komponenten „zerfällt“, wobei die zu diesen Komponenten gehörenden Lose auch unser Ähnlichkeitskriterium erfüllen. Die resultierenden Komponenten sind Cluster.

Bei Verwendung solcher Algorithmen zur Lösung des betrachteten Problems kann eine Situation wie in Abbildung 4 auftreten.


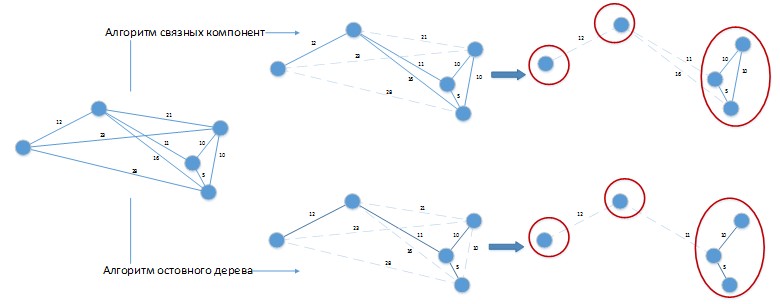Abbildung 4. Anwendung von Clustering-Algorithmen auf das zu lösende Problem.

Angenommen, wir haben einen konstanten Unterschied zwischen den Tagen der Parteien von 20 Tagen. Zählen $$$G$ wurde zur Erleichterung der visuellen Wahrnehmung in räumlicher Form dargestellt. Beide Algorithmen ergaben eine Lösung mit 3 Clustern, die leicht verbessert werden kann, indem Stapel kombiniert werden, die in separaten Clustern untereinander platziert sind! Offensichtlich müssen solche Algorithmen entsprechend den Besonderheiten des zu lösenden Problems weiterentwickelt werden, und ihre reine Anwendung auf die Lösung unseres Problems wird zu schlechten Ergebnissen führen.


Bevor wir also anfingen, den Code der für unsere Aufgabe modifizierten Graph-Algorithmen zu schreiben und unser eigenes Fahrrad zu erfinden (in dessen Silhouetten die Umrisse von Vierkanträdern bereits erraten wurden), beschlossen wir erneut, dieses Problem wissenschaftlich anzugehen, nämlich: versuchen, es auf ein anderes diskretes Problem zu reduzieren Optimierung, in der Hoffnung, dass vorhandene Algorithmen für die Lösung ohne Änderungen angewendet werden können.

Die nächste Suche nach einem ähnlichen klassischen Problem war erfolgreich! Es konnte ein diskretes Optimierungsproblem gefunden werden, dessen Aussage fast 1 zu 1 mit der Aussage unseres Problems übereinstimmt. Dieses Problem stellte sich als das Problem der Abdeckung des Sets heraus . Wir präsentieren die Erklärung des Problems in Bezug auf unsere Besonderheiten.

Es gibt eine endliche Menge $$$P$ und Familie $$$S$ aller seiner disjunkten Untergruppen von Parteien, so dass die Datumsdifferenz für alle Paare von Parteien jeder Untergruppe $$$I$ von der Familie $$$S$ überschreitet nicht die Konstanten $$$C$ . Die Beschichtung wird als Familie bezeichnet $$$U$ geringste Macht, deren Elemente gehören $$$S$ so dass die Vereinigung von Mengen $$$I$ von der Familie $$$U$ sollte viel von allen Parteien geben $$$P$ .

Eine detaillierte Analyse dieses Problems finden Sie hier und hier. Weitere Möglichkeiten zur praktischen Anwendung des Abdeckungsproblems und seiner Modifikationen finden Sie hier.

Der einzige geringfügige Unterschied zwischen dem betrachteten Problem und dem klassischen Problem der Abdeckung einer Menge besteht in der Notwendigkeit, die Anzahl der Elemente in den Teilmengen zu maximieren. Natürlich könnte man nach Artikeln suchen, in denen ein solcher Sonderfall berücksichtigt wurde, und höchstwahrscheinlich würden sie gefunden werden. Bei der nächsten Suche nach Artikeln wurden wir jedoch durch die Tatsache gerettet, dass der bekannte "gierige" Algorithmus zur Lösung des klassischen Problems der Abdeckung einer Menge eine Partition erstellt, die nur die Maximierung der Anzahl der Elemente in den Teilmengen berücksichtigt. Also sind wir ein bisschen voraus gelaufen und jetzt ist alles in Ordnung.

Der Algorithmus zur Lösung des Problems

Wir haben uns für das mathematische Modell des zu lösenden Problems entschieden. Nun beginnen wir, den Algorithmus für seine Lösung zu betrachten. Teilmengen $$$I$ von der Familie $$$S$ kann zum Beispiel durch ein solches Verfahren leicht gefunden werden.

1. Schritt 0. Ordnen Sie die Chargen aus dem Set an $$$P$ in aufsteigender Reihenfolge ihrer Daten. Wir glauben, dass nicht alle Parteien als angesehen markiert sind.
2. Schritt 1. Suchen Sie die Partei mit dem kleinsten Datum aus den Parteien, die noch nicht angezeigt wurden.
3. Schritt 2. Für die gefundene Partei, die sich nach rechts bewegt, nehmen wir sie in die Teilmenge auf $$$I$ alle Parteien, deren Daten sich um höchstens von den aktuellen unterscheiden $$$C$ Tage. Alle im Set enthaltenen Chargen $$$I$ als angesehen markieren.
4. Schritt 3. Wenn beim Verschieben nach rechts die nächste Charge nicht enthalten sein kann $$$I$ Fahren Sie dann mit Schritt 1 fort.

Das Problem beim Abdecken eines Sets ist $$$NP$ - schwierig, was bedeutet, dass es für seine Lösung keinen schnellen (mit einer Betriebszeit gleich einem Polynom aus den Eingabedaten) und genauen Algorithmus gibt. Um das Problem der Abdeckung des Satzes zu lösen, wurde daher ein schneller Greedy-Algorithmus gewählt, der natürlich nicht genau ist, aber die folgenden Vorteile bietet:

• Für Probleme mit kleinen Abmessungen (und dies ist nur unser Fall) werden Lösungen berechnet, die nahe genug am Optimum liegen. Mit zunehmender Größe des Problems verschlechtert sich die Qualität der Lösung, jedoch immer noch ziemlich langsam.
• Sehr einfach zu implementieren;
• Schnell, da die Schätzung seiner Betriebszeit ist $$$O (mn)$ .

Der Greedy-Algorithmus wählt Sätze aus, die von der folgenden Regel geleitet werden: In jeder Phase wird ein Satz ausgewählt, der die maximale Anzahl von Elementen abdeckt, die noch nicht abgedeckt sind. Eine detaillierte Beschreibung des Algorithmus und seines Pseudocodes finden Sie hier. Die Implementierung des Algorithmus in der 1C- Sprache im Spoiler ist geringer (warum sie im nächsten Kapitel damit begonnen haben, ihn in der "gelben" Sprache zu implementieren).


Natürlich kommt die Optimalität eines solchen Algorithmus nicht in Frage - Heuristiken, um nichts zu sagen. Sie können solche Beispiele finden, bei denen ein solcher Algorithmus falsch wäre. Solche Fehler treten auf, wenn wir bei einer Iteration mehrere Sätze mit der gleichen Anzahl von Elementen finden und den ersten auswählen, der auftaucht, weil die Strategie gierig ist: Ich habe das erste genommen, was mir aufgefallen ist, und das „gierige“ war zufrieden.

Es kann durchaus sein, dass eine solche Auswahl bei nachfolgenden Iterationen zu suboptimalen Ergebnissen führt. Aber die Genauigkeit eines so einfachen Algorithmus ist in den meisten Fällen immer noch ziemlich gut. Wenn Sie die Lösung des Problems genauer finden möchten, müssen Sie komplexere Algorithmen verwenden, z. B. wie in der Arbeit : einen probabilistischen Greedy-Algorithmus, einen Ameisenkolonie-Algorithmus usw. Die Ergebnisse des Vergleichs solcher Algorithmen mit den generierten Zufallsdaten sind in der Arbeit zu finden.

Implementierung und Implementierung des Algorithmus

Ein solcher Algorithmus wurde in der 1C- Sprache implementiert und in eine externe Verarbeitung namens "Compression of Residues " einbezogen, die mit dem WMS- System verbunden war. Wir haben den Algorithmus nicht in C ++ implementiert und ihn von einer externen nativen Komponente verwendet, was korrekter wäre, da die Geschwindigkeit von C ++ - Code mehrmals und in einigen Beispielen sogar zehnmal höher ist als die Geschwindigkeit von ähnlichem Code in 1C . In 1C wurde der Algorithmus implementiert, um Entwicklungszeit zu sparen und das Debuggen auf der Arbeitsbasis des Kunden zu vereinfachen. Das Ergebnis des Algorithmus ist in Abbildung 6 dargestellt.


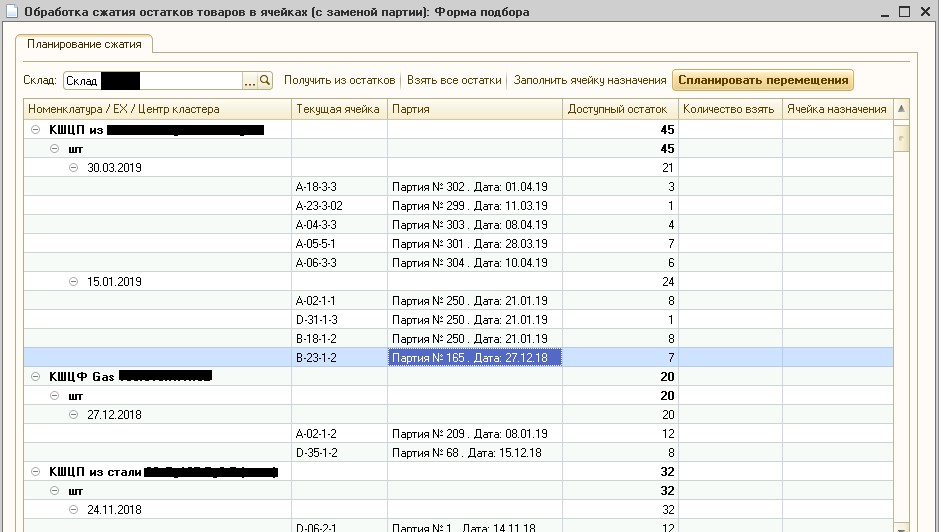Abb. 6. Restkomprimierungsverarbeitung

Abbildung 6 zeigt, dass im angegebenen Lager der aktuelle Warenbestand in Lagerzellen in Cluster unterteilt wurde, in denen sich die Versanddaten um höchstens 30 Tage unterscheiden. Da der Kunde Kugelhähne aus Metall mit einer Haltbarkeit von Jahren herstellt und lagert, kann dieser Datumsunterschied vernachlässigt werden. Beachten Sie, dass diese Verarbeitung derzeit systematisch in der Produktion verwendet wird und WMS- Bediener die gute Qualität des Batch-Clusters bestätigen.

Schlussfolgerungen und weiter

Die wichtigste Erfahrung, die wir bei der Lösung eines solchen praktischen Problems gesammelt haben, besteht darin, die Wirksamkeit der Verwendung des Paradigmas zu bestätigen: Mat. Aufgabenstellung $$$\ rightarrow$ berühmte Matte. das Modell $$$\ rightarrow$ berühmter Algorithmus $$$\ rightarrow$ Algorithmus unter Berücksichtigung der Besonderheiten der Aufgabe. Es gibt bereits mehr als 300 Jahre diskrete Optimierung, und in dieser Zeit gelang es den Menschen, viele Probleme zu berücksichtigen und viel Erfahrung bei der Lösung dieser Probleme zu sammeln. Zunächst ist es ratsamer, sich dieser Erfahrung zuzuwenden und erst dann Ihr Fahrrad neu zu erfinden.

Es ist auch wichtig zu sagen, dass die Lösung des Clustering-Problems nicht getrennt von der Lösung des Problems der Komprimierung des Restes von Chargen betrachtet werden kann, sondern um solche Probleme gemeinsam zu lösen. Das heißt, eine solche Partition von Parteien in Cluster auszuwählen, die die beste Komprimierung ergeben würden. Die Lösung solcher Probleme wurde jedoch aus folgenden Gründen aufgeteilt:

• Begrenztes Budget für die Algorithmusentwicklung. Die Entwicklung eines solchen allgemeinen und damit komplexeren Algorithmus wäre zeitaufwändiger.
• Die Komplexität des Debuggens und Testens. Der allgemeine Algorithmus wäre in der Akzeptanzphase schwieriger zu testen und zu debuggen, und Fehler in ihm wären im Echtzeitbetrieb schwieriger und länger zu debuggen. Zum Beispiel ist ein Fehler aufgetreten und es ist nicht klar, wo gegraben werden soll: Dachfilze in Richtung Clusterbildung, Dachfilze in Richtung Kompression?
• Transparenz und Verwaltbarkeit. Durch die Trennung der beiden Aufgaben wird der Komprimierungsprozess transparenter und damit für Endbenutzer - WMS-Bediener - einfacher zu handhaben. Sie können aus irgendeinem Grund einige Zellen aus der Komprimierung entfernen oder die komprimierbare Menge bearbeiten.

Im nächsten Artikel werden wir die Diskussion über Optimierungsalgorithmen fortsetzen und den interessantesten und viel komplexesten betrachten: den optimalen Algorithmus für die „Komprimierung“ von Residuen in Zellen, der die vom Batch-Clustering-Algorithmus empfangenen Eingaben als Eingaben verwendet.

Einen Artikel vorbereitet
Roman Shangin, Programmierer, Projektabteilung,
Erste BIT-Firma, Tscheljabinsk