Diskrete Mathematik für WMS: Algorithmus zum Komprimieren von Waren in Zellen (Teil 2)

In dem Artikel werden wir beschreiben, wie wir einen Algorithmus zur optimalen Komprimierung der verbleibenden Waren in Zellen entwickelt haben. Wir erklären Ihnen, wie Sie die erforderlichen Metaheuristiken für die Rahmenumgebung des Zoos auswählen: Tabusuche, genetischer Algorithmus, Ameisenkolonie usw.

Wir werden ein Computerexperiment durchführen, um die Betriebszeit und Genauigkeit des Algorithmus zu analysieren. Wir fassen die wertvollen Erfahrungen bei der Lösung dieses Problems der Optimierung und Implementierung von „intelligenten Technologien“ in den Geschäftsprozessen des Kunden zusammen.

Der Artikel ist nützlich für diejenigen, die intelligente Technologien implementieren, in der Lager- oder Produktionslogistikbranche arbeiten, sowie für Programmierer, die sich für mathematische Anwendungen in der Geschäfts- und Prozessoptimierung im Unternehmen interessieren.

Einführungsteil

Diese Veröffentlichung setzt die Artikelserie fort, in der wir unsere erfolgreichen Erfahrungen bei der Implementierung von Optimierungsalgorithmen in Lagerprozessen teilen. Frühere Veröffentlichungen:

• Clustering-Algorithmus für vorrätige Sendungen.
• ein Algorithmus zum Komprimieren von Restgütern in Zellen (Teil 1).

Wie man einen Artikel liest. Wenn Sie die vorherigen Artikel gelesen haben, können Sie sofort mit dem Kapitel "Entwicklung eines Algorithmus zur Lösung des Problems" fortfahren. Wenn nicht, finden Sie unten eine Beschreibung des im Spoiler zu lösenden Problems.

Entwicklung eines Algorithmus zur Lösung des Problems

Bevor mit einer direkten Beschreibung des Optimierungsalgorithmus fortgefahren wird, müssen die Hauptkriterien für die Entwicklung eines solchen Algorithmus angegeben werden, die im Rahmen des Projekts zur Implementierung eines WMS- Systems festgelegt wurden.

• Erstens sollte der Algorithmus leicht zu verstehen sein . Dies ist eine natürliche Voraussetzung, da davon ausgegangen wird, dass der Algorithmus in Zukunft vom IT-Service des Kunden unterstützt und weiterentwickelt wird, was häufig weit von mathematischen Feinheiten und Weisheiten entfernt ist.
• Zweitens sollte der Algorithmus schnell sein . Fast alle Waren im Lager sind an der Komprimierung beteiligt (dies sind ca. 3.000 Artikel), und für jedes Produkt muss ein Dimensionsproblem von ca. 10 x 100 gelöst werden.
• Drittens muss der Algorithmus nahezu optimale Lösungen berechnen.
• Viertens ist die Zeit zum Entwerfen, Implementieren, Debuggen, Analysieren und internen Testen des Algorithmus relativ gering. Dies ist eine wesentliche Voraussetzung, da das Projektbudget , auch für diese Aufgabe, begrenzt war .

Es ist erwähnenswert, dass Mathematiker bis heute viele effektive Algorithmen entwickelt haben, um das Problem des Standortes einer kapazitiven Einrichtung aus einer Hand zu lösen. Betrachten Sie die Hauptvarianten der verfügbaren Algorithmen.

Einige der effizientesten Algorithmen basieren auf dem Ansatz der sogenannten Lagrange-Relaxation. In der Regel handelt es sich dabei um recht komplexe Algorithmen, die für eine Person, die nicht in die Feinheiten der diskreten Optimierung eingetaucht ist, schwer zu verstehen sind. Die „Black Box“ mit komplexen, aber effektiven Algorithmen zur Lagrange-Entspannung des Kunden passte nicht.

Es gibt ziemlich effektive Metaheuristiken (was ist Metaheuristik, die hier gelesen wird, was ist Heuristik, die hier gelesen wird), zum Beispiel genetische Algorithmen, simulierte Annealing-Algorithmen, Ameisenkolonie-Algorithmen, Tabu-Suchalgorithmen und andere (eine Übersicht über solche Metaheuristiken auf Russisch finden Sie hier ). Aber solche Algorithmen haben den Kunden bereits zufrieden gestellt, da:

• Kann Lösungen für Probleme berechnen, die nahezu optimal sind.
• Einfach genug, um zu verstehen, weiter zu unterstützen, zu debuggen und zu verfeinern.
• Sie können schnell eine Lösung für ein Problem berechnen.

Es wurde beschlossen, Metaheuristiken zu verwenden. Jetzt musste nur noch ein „Rahmen“ unter den großen „Zoos“ berühmter Metaheuristiken ausgewählt werden, um das Problem des Standortes einer kapazitiven Einrichtung aus einer Hand zu lösen. Nach Durchsicht einer Reihe von Artikeln, in denen die Wirksamkeit verschiedener Metaheuristiken analysiert wurde, fiel unsere Wahl auf den GRASP-Algorithmus, da er im Vergleich zu anderen Metaheuristiken ziemlich gute Ergebnisse hinsichtlich der Genauigkeit der berechneten Problemlösungen zeigte, einer der schnellsten und vor allem der einfachsten war und transparente Logik.

Das Schema des GRASP-Algorithmus in Bezug auf die Aufgabe "Single Source Capacocated Facility Location Problem" wird im Artikel ausführlich beschrieben . Das allgemeine Schema des Algorithmus ist wie folgt.

• Stufe 1. Generieren Sie eine praktikable Lösung für das Problem durch einen gierigen zufälligen Algorithmus.
• Stufe 2. Verbessern Sie die resultierende Lösung in Stufe 1 mithilfe des lokalen Suchalgorithmus in einer Reihe von Stadtteilen.
• Wenn die Stoppbedingung erfüllt ist, schließen Sie den Algorithmus ab, andernfalls fahren Sie mit Schritt 1 fort. Die Lösung mit den niedrigsten Gesamtkosten unter allen gefundenen Lösungen ist das Ergebnis des Algorithmus.

Die Bedingung zum Stoppen des Algorithmus kann eine einfache Einschränkung der Anzahl von Iterationen oder eine Einschränkung der Anzahl von Iterationen ohne Verbesserung der Lösung sein.


Betrachten wir die Funktionsweise des gierigen randomisierten Algorithmus in Stufe 1 genauer. Es wird angenommen, dass zu Beginn kein einziger Zellcontainer ausgewählt wird.

• Schritt 1. Für jede derzeit nicht ausgewählte Containerzelle wird der Wert berechnet $$$F_ {i} ^ {'}$ Kostenformel
  

  $$

  $$F_ {i} ^ {'} = \ frac {F_ {i}} {N},$$
  wo $$$F_ {i} ^ {'}$ - die Höhe der Kosten für die Auswahl eines Containers $$$i$ und Gesamtkosten für den Warenumzug von $$$N$ Zellen, die noch keinem Container zugeordnet sind, in den Container $$$i$ . So. $$$N$ Zellen werden so ausgewählt, dass das Gesamtvolumen der darin enthaltenen Waren die Kapazität des Containers nicht überschreitet $$$i$ . Spenderzellen werden nacheinander ausgewählt, um in einen Behälterbehälter zu gelangen $$$i$ in der Reihenfolge steigender Kosten für den Transport der Warenmenge in den Container $$$i$ . Die Zellenauswahl wird durchgeführt, bis die Containerkapazität überschritten ist.
• Schritt 2. Gebildeter Satz $$$R$ Container mit Funktionswert $$$F$ den Schwellenwert nicht überschreiten $$$\ min (F) \ cdot (1 + a)$ wo $$$a$ in unserem Fall ist es 0,2.
• Schritt 3. Zufällig aus dem Set $$$R$ Container ist ausgewählt $$$i$ . $$$N$ Zellen, die zuvor im Container ausgewählt wurden $$$i$ In Schritt 1 werden sie schließlich einem solchen Container zugewiesen und nehmen nicht weiter an den Berechnungen des Greedy-Algorithmus teil.
• Schritt 4. Wenn alle Spenderzellen Containern zugeordnet sind, beendet der Greedy-Algorithmus seine Arbeit, andernfalls kehrt er zu Schritt 1 zurück.

Der randomisierte Algorithmus versucht bei jeder Iteration, die Lösung so zu konstruieren, dass ein Gleichgewicht zwischen der Qualität der von ihm konstruierten Lösungen und ihrer Vielfalt besteht. Diese beiden Voraussetzungen für den Start von Entscheidungen sind die Schlüsselbedingungen für den erfolgreichen Betrieb des Algorithmus, da:

• Wenn die Lösungen von schlechter Qualität sind, führt die anschließende Verbesserung in Stufe 2 nicht zu signifikanten Ergebnissen, da wir selbst bei einer Verbesserung der schlechten Lösung sehr oft dieselben Lösungen von schlechter Qualität erhalten.
• Wenn alle Lösungen gut, aber gleich sind, konvergieren die lokalen Suchverfahren zu derselben Lösung. Es ist keineswegs eine Tatsache, dass die optimale Lösung vorliegt. Dieser Effekt wird als Erreichen eines lokalen Minimums bezeichnet und sollte immer vermieden werden.

Nachdem die "Start" -Lösung in Stufe 1 konstruiert wurde, fährt der Algorithmus mit Stufe 2 fort, wo die Verbesserung einer solchen gefundenen Lösung durchgeführt wird, wobei Verbesserung natürlich bedeutet, die Gesamtkosten zu reduzieren. Die Logik des lokalen Suchalgorithmus in Schritt 2 ist wie folgt.

• Schritt 1. Für die aktuelle Lösung $$$S$ Alle "benachbarten" Lösungen werden nach einer Art Nachbarschaft konstruiert $$$N1$ , $$$N2$ , ..., $$$N5$ und für jede "benachbarte" Lösung wird der Wert der Gesamtkosten berechnet.
• Schritt 2. Wenn es unter den benachbarten Lösungen eine bessere Lösung gab $$$S1$ als die ursprüngliche Lösung $$$S$ dann $$$S$ gleich angenommen $$$S1$ und der Algorithmus fährt mit Schritt 1 fort. Andernfalls, wenn es unter den benachbarten Lösungen keine bessere Lösung als die ursprüngliche gab, ändert sich die Ansicht der Nachbarschaft zu einer neuen, die zuvor nicht berücksichtigt wurde, und der Algorithmus fährt mit Schritt 1 fort. Wenn alle verfügbaren Ansichten der Nachbarschaft berücksichtigt werden, aber fehlgeschlagen sind Wenn Sie eine bessere Lösung als das Original finden, beendet der Algorithmus seine Arbeit.

Ansichten der Umgebung werden nacheinander aus dem folgenden Stapel ausgewählt: $$$N1$ , $$$N2$ , $$$N3$ , $$$N4$ , $$$N5$ . Ansichten der Umgebung sind in zwei Typen unterteilt: den ersten Typ (Nachbarschaft $$$N1$ , $$$N2$ , $$$N3$ ), bei denen sich viele Behälter nicht ändern, sondern nur die Optionen zum Anbringen von Spenderzellen ändern; zweiter Typ (Nachbarschaft $$$N4$ , $$$N5$ ), wo sich nicht nur die Optionen zum Anhängen von Zellen an Container ändern, sondern auch die vielen Container selbst.

Wir bezeichnen $$$| J |$ - die Anzahl der Elemente in der Menge $$$J$ . Die folgenden Abbildungen zeigen Optionen für Stadtteile des ersten Typs .


Abb. 7. Nachbarschaft $$$N1$

Nachbarschaft $$$N1$ (oder Shift- Nachbarschaft): Enthält alle Optionen zur Lösung des Problems, die sich vom Original unterscheiden, indem die Anbringung nur einer Spenderzelle am Container geändert wird. Nachbarschaftsgröße nicht mehr $$$| J |$ Optionen.


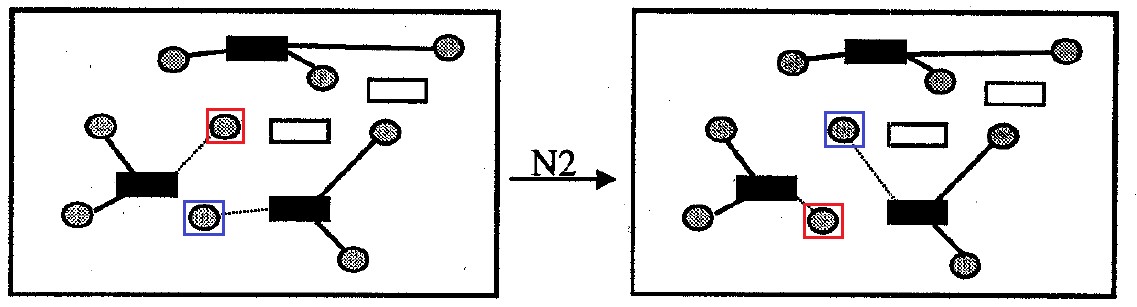Abb. 8. Nachbarschaft $$$N2$


Nachbarschaft $$$N2$ (oder Nachbarschaft tauschen ): Enthält alle Optionen zur Lösung des Problems, die sich vom ursprünglichen durch den gegenseitigen Austausch der Befestigung an Behältern für ein Paar Spenderzellen unterscheiden. Nachbarschaftsgröße nicht mehr $$$| J | ^ 2$ Optionen.


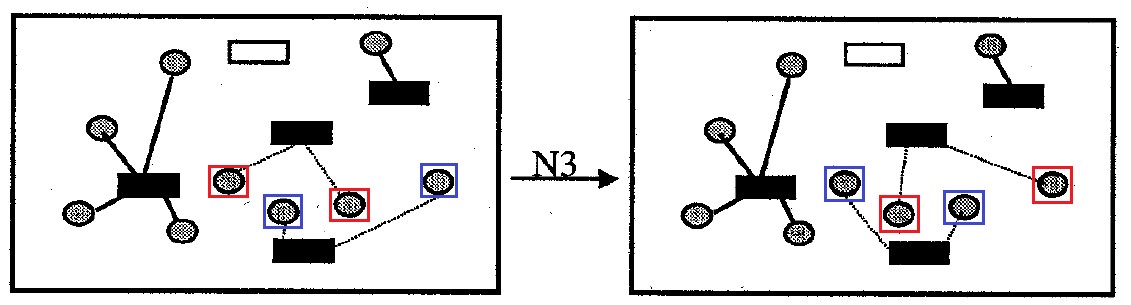Abb. 9. Nachbarschaft $$$N3$

Nachbarschaft $$$N3$ : enthält alle Optionen zur Lösung des Problems, die sich von der ursprünglichen durch gegenseitiges Ersetzen der Anbringung aller Zellen für ein Behälterpaar unterscheiden. Nachbarschaftsgröße nicht mehr $$$| I |$ Optionen.

Die zweite Art von Nachbarschaften wird als Mechanismus der "Diversifizierung" von Entscheidungen angesehen, wenn es bereits unmöglich ist, Verbesserungen durch Durchsuchen der "nahen" Nachbarschaften der ersten Art zu erzielen.


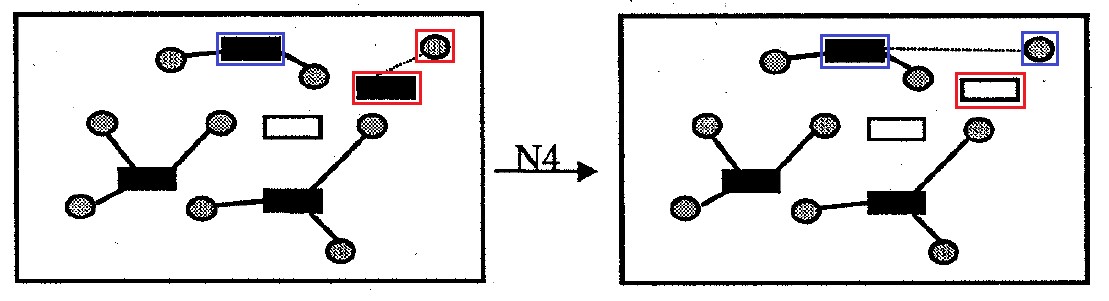Abb. 10. Nachbarschaft $$$N4$

Nachbarschaft $$$N4$ : enthält alle vom Original abweichenden Optionen zur Lösung des Problems, indem eine Containerzelle aus der Lösung entfernt wird. Spenderzellen, die an einem solchen Behälter angebracht waren, der aus der Lösung entfernt wurde, werden an anderen Behältern angebracht, um die Höhe der Transportkosten und die Strafe für das Überschreiten der Kapazität des Behälters zu minimieren. Nachbarschaftsgröße nicht mehr $$$| I |$ Optionen.


Abb. 11. Nachbarschaft $$$N5$

Nachbarschaft $$$N5$ : enthält alle Optionen zur Lösung des Problems, die sich vom ursprünglichen unterscheiden, indem Zellen von einem Container getrennt und solche Zellen für ein beliebiges Paar von Containern an einen anderen leeren Container angehängt werden. Nachbarschaftsgröße nicht mehr $$$| I | ^ 2$ Optionen.

Die Autoren des Artikels sagen, dass basierend auf den Ergebnissen von Computerexperimenten die beste Option darin besteht, zuerst nach "nahen" Nachbarschaften des ersten Typs und dann nach "entfernten" Nachbarschaften zu suchen.

Beachten Sie, dass die Autoren des Artikels empfehlen, eine Suche in der Nähe durchzuführen, ohne die Kapazitätsbeschränkungen der einzelnen Container zu berücksichtigen. Wenn stattdessen die Kapazität des Behälters überschritten wird, addieren Sie zu den Gesamtkosten der Lösung eine positive Menge an „Fein“, was die Attraktivität einer solchen Lösung im Vergleich zu anderen Lösungen beeinträchtigt. Die einzige Beschränkung gilt für das Gesamtvolumen der Container, dh das Gesamtvolumen der von Spenderzellen transportierten Waren sollte die Gesamtkapazität der Container nicht überschreiten. Diese Aufhebung von Einschränkungen erfolgt, da unter Berücksichtigung von Einschränkungen die Nachbarschaft häufig keine einzige akzeptable Lösung enthält und der lokale Suchalgorithmus seine Arbeit unmittelbar nach dem Start beendet, ohne dass Verbesserungen vorgenommen werden. Abbildung 12 zeigt ein Beispiel für einen lokalen Suchvorgang ohne Berücksichtigung von Kapazitätsbeschränkungen für jeden Container.


Abb. 12. Die Arbeit der lokalen Suche ohne Berücksichtigung von Kapazitätsbeschränkungen für jeden Container

In dieser Figur wird angenommen, dass die roten und grünen Reste einiger Spenderzellen nicht vorteilhaft sind, um in einen anderen Behälter außer dem zweiten zu gelangen. Dies bedeutet, dass eine weitere Verbesserung der Lösung unmöglich ist, da jede andere neue mögliche Lösung des Problems, bei der die Kapazitätsbeschränkungen eingehalten werden, hinsichtlich der Transportkosten schlechter ist als das Original. Wie Sie sehen können, erstellt der Algorithmus für 2 Iterationen eine praktikable Lösung, die viel besser als das Original ist, obwohl die erste Iteration eine ungültige Lösung mit überschüssiger Kapazität erstellt.

Beachten Sie, dass dieser Ansatz der Einführung einer „Strafe“ für die Unzulässigkeit einer Lösung bei der diskreten Optimierung durchaus üblich ist und häufig in Algorithmen wie genetischen Algorithmen, Tabusuche usw. verwendet wird.

Nachdem der lokale Suchalgorithmus abgeschlossen ist und die gefundene Lösung immer noch nicht akzeptabel ist, dh die Containerkapazitätsgrenzen irgendwo überschritten wurden, müssen wir die gefundene Lösung in eine akzeptable Form bringen, in der alle Einschränkungen der Containerkapazität eingehalten werden. Der Algorithmus zum Beheben der Unzulässigkeit der Lösung ist wie folgt.

• Schritt 1. Führen Sie eine lokale Suche in den Stadtteilen Shift und Swap durch . In diesem Fall wird der Übergang nur in den Entscheidungen durchgeführt, die genau die Höhe der „Geldbuße“ reduzieren. Ist die Reduzierung der Strafe nicht möglich, wird eine Lösung mit geringeren Gesamtkosten gewählt. Wenn eine weitere Verbesserung durch lokale Suche in keiner Weise möglich ist, fahren Sie mit Schritt 2 fort. Andernfalls vervollständigen Sie den Algorithmus, wenn die resultierende Lösung gültig ist.
• Schritt 2. Wenn die Lösung immer noch nicht akzeptabel ist, werden von jedem Behälter, in dem ein Kapazitätsüberschuss vorhanden war, Spenderzellen in der Reihenfolge des zunehmenden Warenvolumens abgelöst, bis die Kapazitätsbeschränkung erreicht ist. Für solche getrennten Zellen werden alle Schritte des Algorithmus, beginnend mit dem ersten, wiederholt, obwohl der Satz verfügbarer ausgewählter Container und die Art und Weise, wie die verbleibenden Zellen an sie angehängt werden, festgelegt sind und nicht geändert werden können. Es ist zu beachten, dass ein solcher Schritt 2, wie das Computerexperiment zeigt, äußerst selten durchgeführt werden muss.

Computerexperiment und Analyse der Algorithmuseffizienz

Der GRASP-Algorithmus wurde in C ++ von Grund auf neu implementiert, da wir den Quellcode für den im Artikel beschriebenen Algorithmus nicht gefunden haben. Der Programmcode wurde mit g ++ mit der Optimierungsoption -O2 kompiliert.

Visual Studio-Projektcode ist auf GitHub verfügbar. Das einzige, was der Kunde verlangte, war, einige der komplexesten lokalen Suchverfahren aus Gründen des geistigen Eigentums, Geschäftsgeheimnissen usw. zu entfernen.

In dem Artikel , der den GRASP-Algorithmus beschreibt, wurde seine hohe Effizienz angegeben, wobei unter Effizienz zu verstehen ist, dass er Lösungen sehr nahe am Optimum stabil berechnet und recht schnell funktioniert. Um die tatsächliche Wirksamkeit eines solchen GRASP-Algorithmus zu überprüfen, haben wir unser eigenes Computerexperiment durchgeführt. Die Eingabedaten des Problems wurden von uns zufällig mit einer gleichmäßigen Verteilung generiert. Die vom Algorithmus berechneten Lösungen wurden mit den optimalen Lösungen verglichen, die mit dem im Artikel vorgeschlagenen genauen Algorithmus berechnet wurden. Quellen eines solchen exakten Algorithmus sind auf GitHub als Referenz frei verfügbar. Die Dimension der Aufgabe, zum Beispiel 10x100, bedeutet, dass wir 10 Spenderzellen und 100 Behälterzellen haben.

Die Berechnungen wurden auf einem Personal Computer mit den folgenden Eigenschaften durchgeführt: CPU 2,50 GHz, Intel Core i5-3210M, 8 GB RAM, Windows 10 (x64) Betriebssystem.
Tabelle 3. Vergleich der Betriebszeit des GRASP-Algorithmus und des genauen Algorithmus

Wie aus Tabelle 3 ersichtlich ist, berechnet der GRASP-Algorithmus tatsächlich nahezu optimale Lösungen, und mit zunehmender Dimension des Problems verschlechtert sich die Qualität der Algorithmuslösungen geringfügig. Aus den Ergebnissen des Experiments geht auch hervor, dass der GRASP-Algorithmus ziemlich schnell ist, beispielsweise löst er ein 10x100-Dimensionsproblem im Durchschnitt in 0,5 Sekunden. Am Ende ist zu erwähnen, dass die Ergebnisse unseres Computerexperiments mit den Ergebnissen im Artikel übereinstimmen .

Ausführen des Algorithmus in der Produktion

Nachdem der Algorithmus in einem Computerexperiment entwickelt, debuggt und getestet worden war, war es an der Zeit, ihn in Betrieb zu nehmen. Der Algorithmus wurde in C ++ implementiert und in eine DLL gestellt, die als externe Komponente des Native-Typs mit der 1C- Anwendung verbunden war . Die Tatsache , dass solche externen Komponenten 1C und wie man richtig entwickeln und an die Anwendung anschließen 1C lesen hier . Im Programm „1C: Warehouse Management 3“ wurde ein Verarbeitungsformular entwickelt, in dem der Benutzer das Verfahren zum Komprimieren von Residuen mit den von ihm benötigten Parametern starten kann. Ein Screenshot des Formulars ist unten dargestellt.


Abb. 13. Die Form des Verfahrens zur „Komprimierung“ von Salden in Anhang 1C: Lagerverwaltung 3

Der Benutzer kann die Komprimierungsparameter für Rückstände in folgender Form auswählen:

• Komprimierungsmodus: mit und ohne Clustering von Stapeln (siehe ersten Artikel).
• Lager, in dessen Zellen eine Komprimierung durchgeführt werden muss. In einem Raum können sich mehrere Lager für verschiedene Organisationen befinden. Genau so war es bei unserem Kunden.
• Außerdem kann der Benutzer die Menge der von der Spenderzelle in den Container übertragenen Waren interaktiv anpassen und den Artikel zur Komprimierung aus der Liste löschen, wenn er aus irgendeinem Grund möchte, dass er nicht am Komprimierungsvorgang teilnimmt.

Fazit

Am Ende des Artikels möchte ich die Erfahrungen zusammenfassen, die durch die Einführung eines solchen Optimierungsalgorithmus gewonnen wurden.

• . : , , . - :
  
  1. , ;
  2. .
• ( ), , . «», - . , , . , , , - , .
• , ( ), . , , . , . . , .
• :
  
  1. .
  2. .
  3. . , .
  4. . , . , , , , .
  5. , . ( ) . , .
  6. .

Und ich denke, das Wichtigste. Der Optimierungsprozess im Unternehmen muss häufig nach Abschluss des Informatisierungsprozesses erfolgen. Eine Optimierung ohne vorläufige Informatisierung ist wenig nützlich , da es keinen Ort gibt, von dem Daten abgerufen werden können, und keinen Ort, an dem die Lösungsdaten des Algorithmus geschrieben werden können. Ich denke, dass die Mehrheit der mittleren und großen inländischen Unternehmen die Grundbedürfnisse nach Automatisierung und Informatisierung geschlossen hat und bereit ist, die Prozessoptimierung weiter zu optimieren.

Daher üben wir nach der Implementierung des Informationssystems, sei es ERP, WMS, TMS usw. kleines extra machen. Projekte zur Optimierung der Prozesse, die bei der Implementierung des Informationssystems als problematisch und wichtig für den Kunden identifiziert wurden. Ich denke, dies ist eine vielversprechende Praxis, die in den kommenden Jahren an Dynamik gewinnen wird.


, ,
, .