Untersuchung des Magnetschwebesystems zur Modalsteuerung

Dieses Material wurde im Hinblick auf die bisherige Verteidigung der endgültigen Qualifikationsarbeit des Bachelor unter Berücksichtigung einiger Kommentare zum Kontrollobjekt erstellt. Das Material wird als erste Reserve für eine mögliche Masterarbeit zum gleichen Thema angelegt.

Zunehmend werden moderne Magnetschwebesysteme eingesetzt: Hochgeschwindigkeits-Personenzüge, Isolation schwingungsempfindlicher Mechanismen, Magnetlager, Schweben von Metallschmelze in Induktionsöfen sowie Schweben von Metallknüppeln. In letzter Zeit wird der Effekt der Magnetschwebebahn auch in Haushaltsgeräten verwendet.

Die vielleicht bedeutendste Anwendung wurde in Zügen mit einem Schwebesystem auf Supraleitern gefunden. Dies liegt an Vorteilen wie einer höheren Zuverlässigkeit (aufgrund mangelnder Reibung), einem relativ geringen Stromverbrauch und der Fähigkeit, eine hohe Geschwindigkeit zu entwickeln.

Aufgrund der nichtlinearen Bewegungsgleichungen des Objekts, die seine Dynamik beschreiben, ist es jedoch schwierig, den Prozess der Steuerung des Objekts zu reproduzieren. Es geht um die Position (Entfernung) des Objekts relativ zur Nullmarke.

Kurz gesagt, Magnetschwebebahn ist eine stabile Position eines Objekts in einem bestimmten Abstand in einem Gravitationsfeld, wenn die Erdbeschleunigung in der Regel durch die Beschleunigung des Objekts kompensiert wird, die durch ein Magnetfeld erzeugt wird. In diesem Fall entsteht eine Hubkraft.

Die Magnetschwebebahn wird mit Hilfe von Diamagneten, Wirbelstromsystemen und Supraleitern sowie mit Hilfe von Servomechanismen realisiert.

Im aktuellen Artikel (unter dem Schnitt) werden wir die Modalsteuerung für ein linearisiertes System der Magnetschwebebahn sowie die Implementierung der Modalsteuerung für ein nichtlineares Modell des Systems betrachten.

Mathematisches Modell

Betrachten Sie ein einfaches Magnetschwebeschema.

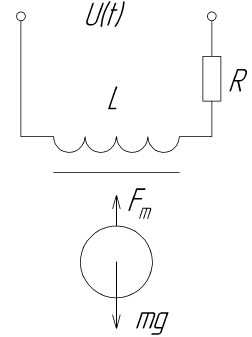
Dieses Diagramm zeigt einen Elektromagneten, der mit dem Magnetfeld des Steuerobjekts interagiert, bei dem es sich um einen Kugel-Permanentmagneten handelt. Durch eine Änderung der Anziehungskraft des Elektromagneten wird der Schwebeeffekt erreicht.

In der letzten Arbeit wurde ein Objekt zweiter Ordnung betrachtet, bei dem eine wichtige Komponente, der Strom in der Spule, nicht im Zustandsvektor enthalten war. Dieses Mal wird diese Komponente eingeführt.

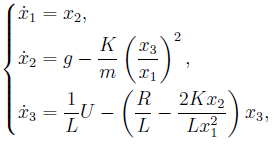
wo $$$x_1$- Position des Objekts;

$$$x_2$- die Änderungsrate der Position des Objekts;

$$$g$- Beschleunigung der Schwerkraft;

$$$K$Ist eine Konstante;

$$$m$- Masse des Ballobjekts;

$$$x_3$- Strom in der Spule;

$$$L$- Spuleninduktivität;

$$$U$- Eingangsspannung;

$$$R$- aktiver Widerstand der Spule.

Die Werte einiger der oben genannten Variablen sind in einer Tabelle zusammengefasst.

Um ein lineares Modell zu erhalten, sollte man das Gleichungssystem linearisieren.

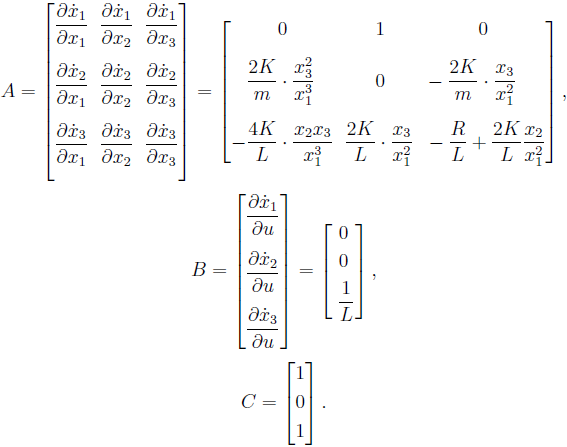
Matrixansicht $$$C$kann durch die Tatsache gerechtfertigt werden, dass solche Zustandsvektorvariablen wie Position ( $$$x_1$) und aktuell ( $$$x_3$)

In dieser Form sind die resultierenden Matrizen immer noch nicht für die Modellierung geeignet. Dazu legen wir die Ausgangsbedingungen fest.

$$

$$x_1 ^ {\ left \ {0 \ right \}} = 0,005, ~ x_2 ^ {\ left \ {0 \ right \}} = 0.$$

$$

$$g - \ frac {K (x_3 ^ {\ left \ {0 \ right \}}) ^ 2} {m (x_1 ^ {\ left \ {0 \ right \}}) ^ 2} = 0$$

$$

$$x_3 ^ {\ left \ {0 \ right \}} = \ sqrt {\ frac {gm} {K}} x_1 ^ {\ left \ {0 \ right \}} = 0,063 ~ \ text {A}.$$

Ersetzen Sie nun die erhaltenen Daten und $$$x_3 ^ {\ left \ {0 \ right \}}$ So ermitteln Sie den Wert des Eingangssignals zum Anfangszeitpunkt:

$$

$$U ^ {\ left \ {0 \ right \}} = \ left (R - \ frac {2Kx_2 ^ {\ left \ {0 \ right \}}} {(x_1 ^ {\ left \ {0 \ right \ }}) ^ 2} \ right) x_3 ^ {\ left \ {0 \ right \}} = Rx_3 ^ {\ left \ {0 \ right \}} = 1,95 ~ \ text {B}.$$

Modellierung

Jetzt können Sie die Steuerung synthetisieren. Für die Forschung wurde das Matlab-Paket ausgewählt. Unten ist der Code zum Erhalten der Reglerkoeffizienten nach Zustand:

g = 9.81; K = 0.659*10^-3; m = 0.0106; L = 0.109; R = 31.1; x10 = 0.005; x20 = 0; x30 = sqrt(g*m/K)*x10; u = R*x30; A = [0 1 0; 2*K*x30^2/(m*x10^3) 0 -2*K*x30/(m*x10^2); -4*K*x20*x30/(L*x10^3) 2*K*x30/(L*x10^2) -R/L+2*K*x20/(L*x10^2)]; B = [0; 0; 1/L]; C = [1 0 0]; W = ctrb(A, B); %   detW = det(W); poles = [-10 -10 -10]; %  K = acker(A, B, poles); %  system = ss(A - B*K, B, C, 0); %   figure(1) step(system) %   km = 1/dcgain(system); %   system_m = ss(A - B*K, B*km, C, 0); figure(2) step(system_m) 

Um zu verstehen, ob es möglich ist, die Steuerung für das resultierende System zu synthetisieren, müssen Sie die Steuerbarkeitsmatrix kennen, anhand deren Determinante die Schlussfolgerung gezogen wird:

 >> detW detW = -7.5351e+07 

Die Determinante ist ungleich Null, daher ist das linearisierte System steuerbar.

Die Vektorpole sind Vektoren, die die gewünschten Pole des linearisierten Magnetschwebesystems enthalten.

Wenn wir den Testeffekt in Form eines einzelnen Schritts anwenden, erhalten wir das folgende Ergebnis:

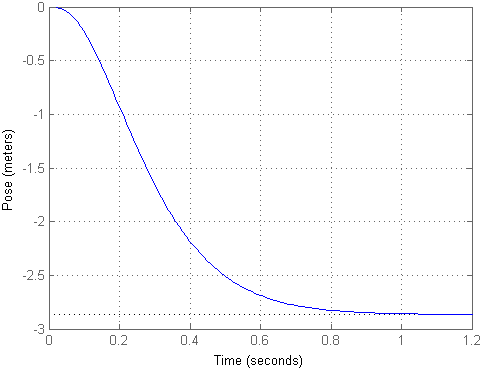
Wie Sie sehen können, stellte sich heraus, dass das Objekt mit geringem Aufprall eine ziemlich große Strecke flog, obwohl es in derselben Position blieb. Damit der Eingang dem Ausgang entspricht, können wir den Skalierungsfaktor km berechnen und das Eingangssignal damit multiplizieren, was im zweiten Modell realisiert wurde. Dann sieht der Übergangsprozess folgendermaßen aus:

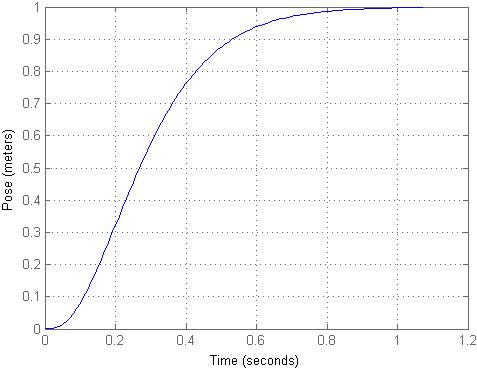
Die resultierende Position ist für eine solche Installation immer noch großartig. Lassen Sie uns zunächst den Strom ignorieren und direkt zu den Simulink-Modellen gehen, wo wir die verbleibenden Dinge betrachten.

Wir skalieren das Eingangssignal so, dass die Ausgangswerte bequem in Zentimetern dargestellt werden. Wir wenden verschiedene Testaktionen auf den Eingang an, um zu überprüfen, wie Transienten im System aussehen und wie der Strom fließt.

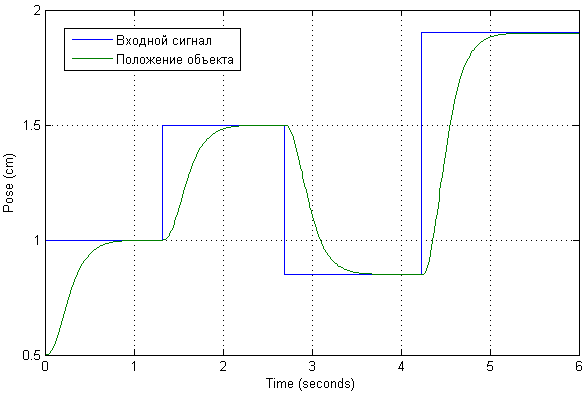
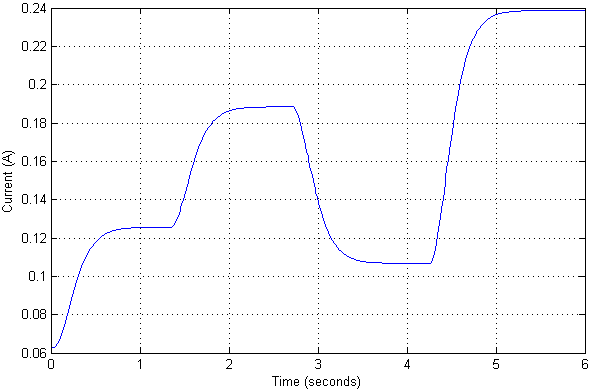
Es stellt sich heraus, dass der aktuelle Wert an solchen Positionen des Objekts nicht so signifikant ist. Die Transienten selbst in Position sind aperiodischer Natur, ohne Überschwingen und statischen Fehler. Eigentlich wurde es durch die gewünschten Pole des eingestellten Systems eingestellt.

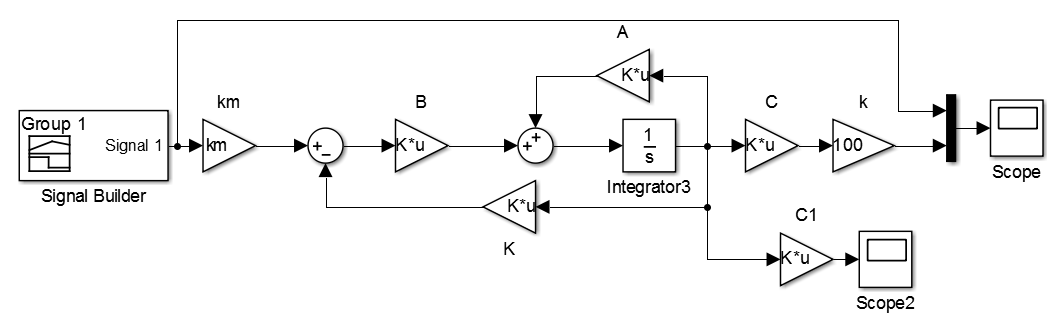
Diese Annäherung im Betriebspunkt funktioniert jedoch möglicherweise nicht richtig mit dem ursprünglichen nichtlinearen Modell. Überprüfen Sie dies heraus. Ein nichtlineares Systemmodell mit angeschlossener Steuerung ist unten dargestellt.

Dies ist die endgültige Version, die nach allen Experimenten übrig bleibt. Die Eingangsspannung (0-12 V) und die Position des Objekts selbst (0-4 cm) wurden begrenzt. Die zweite Komponente des Reglers wurde ausgeschlossen, da damit der Übergangsprozess instabil war:

Nach Änderungen an der Schaltung sehen Transienten nun folgendermaßen aus:

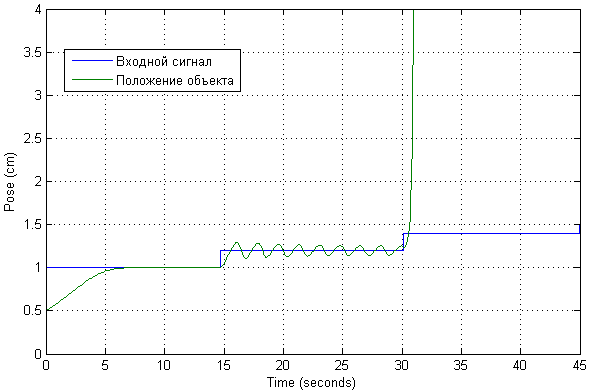
Der mögliche Betriebsbereich eines solchen Systems wurde sofort überprüft. Sie sehen, dass die gewünschte Position mit geringfügigen Abweichungen vom Startpunkt erreicht wird. In diesem Fall ist eine Manifestation einer signifikanten Schwingung möglich.

In diesem Fall lautet der aktuelle Wert wie folgt:

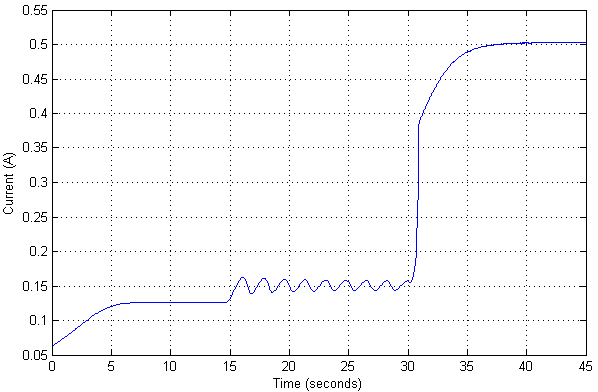
Da bereits ein nichtlineares Modell eines Objekts überprüft wurde, können Sie auch den maximalen Positionswert für ein Objekt anzeigen, bei dem es immer noch nicht an Stabilität verliert.

Nach der Modellierung mit verschiedenen Eingangssignalen wurde festgestellt, dass das linearisierte Modell sehr gut ist. Hier werden wir also Transienten gemäß dem um das Zehnfache erhöhten Eingangssignal demonstrieren.

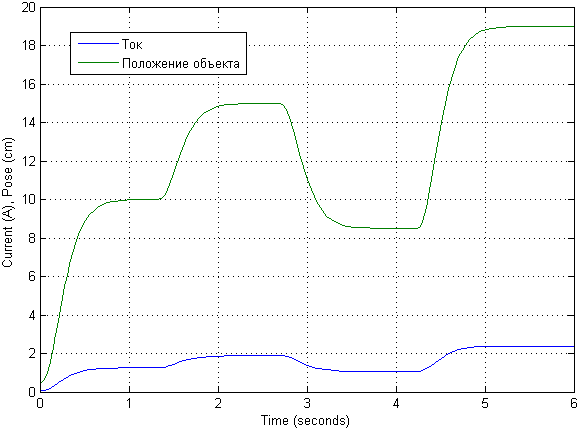
Das mathematische Modell selbst könnte etwas anders aussehen. Ihre Beschreibung stammt aus der Beschreibung des mathematischen Modells .

Fazit

Die Modalsteuerung für dieses nichtlineare Modell eines Magnetschwebesystems ist für keine praktischen Anforderungen geeignet. Andere Implementierungen für dieses Magnetschwebesystem sollten in Betracht gezogen werden.

Für die Bachelorarbeit hat der Autor eine einfache Levitationsinstallation implementiert, die in Zukunft separat beschrieben wird.