Auffinden einer unbeaufsichtigten Objekterkennung

Eine der wichtigsten Aufgaben beim maschinellen Lernen ist die Objekterkennung. Kürzlich wurde eine Reihe von Algorithmen für maschinelles Lernen veröffentlicht, die auf Deep Learning zur Objekterkennung basieren. Diese Algorithmen nehmen einen zentralen Platz in praktischen Computer-Vision-Anwendungen ein, insbesondere die derzeit sehr beliebten selbstfahrenden Autos. Aber alle diese Methoden sind Lehrmethoden mit einem Lehrer, d.h. Sie benötigen einen riesigen Datensatz (einen riesigen Datensatz). Natürlich besteht der Wunsch nach einem Modell, das aus „rohen“ (nicht zugewiesenen) Daten lernen kann. Ich habe versucht, bestehende Methoden zu analysieren und mögliche Entwicklungsmöglichkeiten aufzuzeigen. Ich frage alle, die unter kat Gnade wünschen, es wird interessant sein.

Aktueller Status der Frage

Natürlich gibt es die Formulierung dieses Problems schon lange (fast seit den ersten Tagen des maschinellen Lernens), und es gibt eine ausreichende Anzahl von Arbeiten zu diesem Thema. Zum Beispiel eine meiner bevorzugten räumlich invarianten unbeaufsichtigten Objekterkennungen mit Faltungs-Neuronalen Netzen . Kurz gesagt, die Autoren trainieren VAE (Variable Auto Encoder), aber dieser Ansatz wirft für mich eine Reihe von Fragen auf.

Ein bisschen Philosophie

Was ist ein Objekt in einem Bild? Um diese Frage zu beantworten, müssen wir die Frage beantworten: Warum teilen wir die Welt überhaupt in Objekte? Nach einigem Nachdenken über diese Frage hatte ich nur eine Antwort auf diese Frage (ich sage nicht, dass es keine anderen gibt, ich habe sie nur nicht gefunden) - wir versuchen, eine Darstellung der Welt zu finden, die für uns leicht zu verstehen und zu kontrollieren ist, wie viele Informationen zur Beschreibung der Welt benötigt werden im Kontext der aktuellen Aufgabe. Zum Beispiel für die Aufgabe der Klassifizierung von Bildern (die im Allgemeinen falsch formuliert ist - es gibt sehr selten Bilder mit einem Objekt. Das heißt, wir lösen das Problem nicht, was auf dem Bild gezeigt wird, sondern welches Objekt "Haupt" ist), müssen wir nur sagen, dass das Bild "Auto" ist. Um Objekte zu erkennen, möchten wir wiederum wissen, welche „interessanten“ Objekte (wir interessieren uns nicht für alle Blätter der Bäume auf dem Bild) vorhanden sind und wo sie sich befinden, um die Szene zu beschreiben, den Namen des „interessanten“ Prozesses zu erhalten es passiert dort zum Beispiel "Sonnenuntergang" usw.

Es stellt sich heraus, dass Objekte eine bequeme Darstellung von Daten sind. Welche Eigenschaften sollte diese Darstellung haben? Die Ansicht sollte so viele vollständige Informationen wie möglich über das Bild enthalten. Das heißt, Mit einer Objektbeschreibung möchten wir in der Lage sein, das Originalbild mit der erforderlichen Genauigkeit wiederherzustellen.

Wie kann dies mathematisch ausgedrückt werden? Stellen Sie sich vor, das Bild ist eine Realisierung einer Zufallsvariablen X, und die Darstellung ist eine Realisierung einer Zufallsvariablen Y. In Anbetracht des oben Gesagten möchten wir, dass Y so viele Informationen wie möglich über X enthält. Verwenden Sie dazu natürlich das Konzept der gegenseitigen Information.

Modelle für maschinelles Lernen für maximale Information

Die Erkennung von Objekten kann als generatives Modell betrachtet werden, das am Eingang ein Bild empfängt $$$x$und die Ausgabe ist eine Objektdarstellung des Bildes $$$y$.

Erinnern wir uns nun an die Formel zur Berechnung der gegenseitigen Information:

$$

$$I (x, y) = \ int p (x, y) log \ frac {p (x, y)} {p (x) p (y)} dxdy$$

wo $$$p (x, y)$Verteilung der Gelenkdichte ebenfalls $$$p (x), p (y)$marginalisiert.

Hier werde ich nicht weiter darauf eingehen, warum diese Formel so aussieht, aber wir werden glauben, dass sie intern sehr logisch ist. Übrigens ist es aufgrund der beschriebenen Überlegungen nicht erforderlich, genau gegenseitige Informationen auszuwählen, es können auch andere „Informationen“ sein, aber wir werden näher am Ende darauf zurückkommen.

Besonders aufmerksame (oder diejenigen, die Bücher über die Theorie der Information lesen) haben bereits bemerkt, dass gegenseitige Information nichts anderes ist als die Kullback-Lebler-Divergenz zwischen der gemeinsamen Verteilung und der Arbeit von Randgruppen. Hier tritt eine leichte Komplikation auf: Jeder, der mindestens ein paar Bücher über maschinelles Lernen gelesen hat, weiß, dass wenn wir nur Beispiele aus zwei Verteilungen haben (d. H. Wir kennen die Verteilungsfunktionen nicht), es nicht einmal optimiert, sondern sogar die Divergenz von Kullback bewertet. Leiblers Aufgabe ist nicht trivial. Darüber hinaus wurden unsere geliebten GANs genau aus diesem Grund geboren.

Glücklicherweise hilft uns die wunderbare Idee, die unter Über Variationsgrenzen gegenseitiger Information beschriebene untere Variationsgrenze zu verwenden. Gegenseitige Informationen können dargestellt werden als:

$$

$$I (x, y) = \ int p (x) dx \ int p (y | x) log [q (x | y)] dxdy + \ int p (y) dy \ int p (x | y) log (\ frac {p (x | y)} {q (x | y)} dxdy$$

Oder

$$

$$I (x, y) = \ int p (x) dx \ int p (y | x) log [q (x | y)] dxdy + KL [p (x | y) || q (x | y) ]$$

wo $$$p (y | x)$- die Verteilung der Darstellung für ein bestimmtes Bild, die von unserem neuronalen Netzwerk parametrisiert wird, und aus dieser Verteilung können wir eine Stichprobe erstellen, aber wir müssen nicht in der Lage sein, die Dichte oder Wahrscheinlichkeit einer bestimmten Stichprobe zu bewerten (was im Allgemeinen für viele generative Modelle typisch ist). $$$q (x | y)$Ist eine bestimmte Dichtefunktion durch das zweite neuronale Netzwerk parametrisiert (im allgemeinsten Fall benötigen wir 2 neuronale Netzwerke, obwohl sie in einigen Fällen durch das erste dargestellt werden können), müssen wir hier in der Lage sein, die Wahrscheinlichkeiten der resultierenden Stichproben zu berechnen.

Wert $$$LVB (x, y) = \ int p (x) dx \ int p (y | x) log [q (x | y)] dxdy$genannt die untere Variationsgrenze.

Jetzt können wir die Herangehensweise an unser Problem lösen, nämlich nicht die gegenseitige Information selbst, sondern ihre untere Variationsgrenze zu erhöhen. Wenn die Verteilung $$$q (x | y)$richtig gewählt, dann am maximalen Punkt der Variationsgrenze und gegenseitige Information zusammenfallen, aber im praktischen Fall (wenn die Verteilung $$$q (x | y)$kann mir nicht genau vorstellen $$$p (x | y)$, besteht aber aus einer ziemlich großen Familie von Funktionen) wird sehr eng sein, was auch zu uns passt.

Wenn jemand nicht weiß, wie das funktioniert, empfehle ich Ihnen, den EM-Algorithmus sorgfältig zu prüfen. Hier ist ein völlig ähnlicher Fall.

Was ist hier los? Tatsächlich haben wir die Funktionalität zum Trainieren von Auto-Encodern erhalten. Wenn Y das Ergebnis am Ausgang eines neuronalen Netzwerks mit einem Bild am Eingang ist, bedeutet dies, dass $$$p (y | x) = \ delta (enc (x))$wo $$$enc (x)$neuronale Netzwerk-Transformationsfunktion. Und approximieren Sie die inverse Verteilung durch Gauß, d.h. $$$log [q (x | y)] = (x - dec (y)) ^ 2 - 2 * log (Sigma)$wir bekommen:

$$

$$LVB (x, y) = \ int p (x) (x-dec (enc (x))) ^ 2dx + C$$

Und dies ist eine klassische Funktion für Auto-Encoder.

Auto Encoder ist nicht genug

Ich denke, dass viele den Auto-Encoder bereits trainieren wollen und hoffen, dass es in seiner verborgenen Schicht Neuronen gibt, die auf bestimmte Objekte reagieren. Im Allgemeinen gibt es eine Bestätigung für etwas Ähnliches, und es stellt sich heraus, dass mithilfe von unbeaufsichtigtem Lernen in großem Maßstab Funktionen auf hoher Ebene erstellt werden . Dies ist jedoch völlig unpraktisch. Und die aufmerksamsten Leute haben bereits bemerkt, dass die Autoren dieses Artikels Regularisierung verwendeten - sie fügten einen Begriff hinzu, der die verborgene Ebene spärlich macht, und sie schrieben in Schwarzweiß, dass nichts dergleichen ohne diesen Begriff passiert.

Reicht das Prinzip der Maximierung der gegenseitigen Information aus, um eine „bequeme“ Idee zu erlernen? Offensichtlich nicht, da wir Y gleich X wählen können (dh das Bild selbst als Repräsentation verwenden) oder eine bijektive Transformation, geht die gegenseitige Information in diesem Fall ins Unendliche. Von diesem Wert kann es keinen mehr geben, aber wie wir wissen, ist dies eine sehr schlechte Idee.

Wir brauchen ein zusätzliches Kriterium für die „Bequemlichkeit“ der Präsentation. Die Autoren des obigen Artikels betrachteten Spärlichkeit als "Bequemlichkeit". Dies ist eine Art Verwirklichung der Hypothese, dass das Bild einige „wichtige Objekte“ enthalten sollte. Aber wir werden noch weiter gehen - wir wollen nicht nur lernen, dass sich ein solches Objekt auf dem Bild befindet, sondern auch wissen, wo es sich befindet, wie stark es sich überlappt usw. Es stellt sich die Frage, wie das neuronale Netzwerk die Ausgabe eines Neurons wie beispielsweise die Koordinate eines Objekts interpretieren kann. Die Antwort liegt auf der Hand - die Ausgabe dieses Neurons sollte genau dafür verwendet werden. Das heißt, wenn wir die Idee kennen, müssen wir in der Lage sein, „ähnliche“ Bilder wie das Original zu erzeugen.

Die allgemeine Idee wurde von den Jungs von Facebook entlehnt.
Der Encoder sieht folgendermaßen aus:

wo $$$A$- ein Vektor, der das Objekt beschreibt, $$$x, y$- Koordinaten des Objekts, $$$sx, sy$- die Größe des Objekts, $$$z$- die Position des Objekts in der Tiefe, $$$p$- die Wahrscheinlichkeit, dass das Objekt vorhanden ist.

Das heißt, das neuronale Eingangsnetzwerk empfängt ein Bild einer vorbestimmten Größe, auf dem wir Objekte finden möchten, und gibt eine Reihe von Beschreibungen aus. Wenn wir ein Single-Pass-Netzwerk wollen, muss dieses Array leider eine feste Größe haben. Wenn wir alle Objekte finden wollen, müssen wir Rekrutierungsnetzwerke verwenden.

Der Decoder sieht folgendermaßen aus:


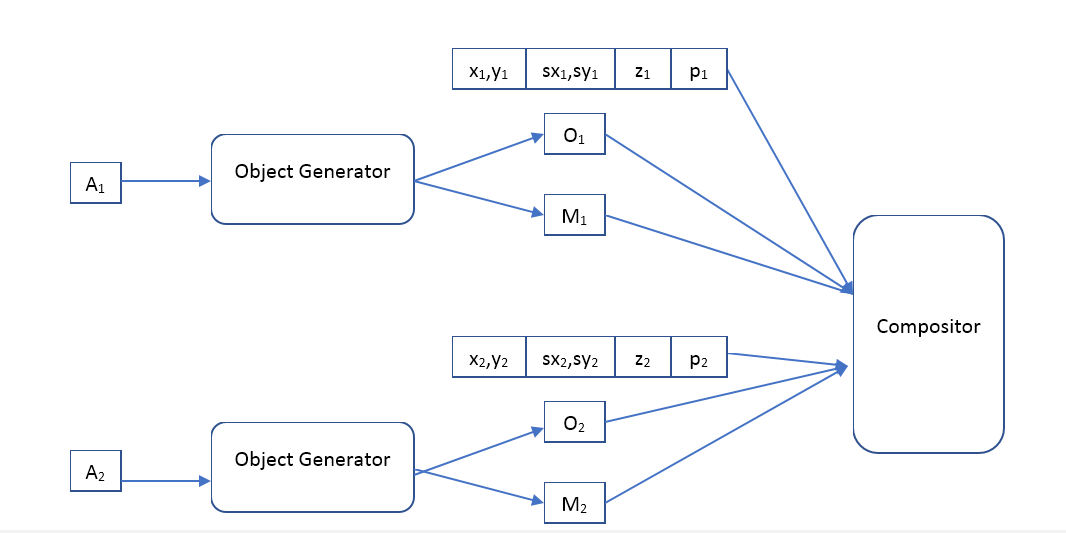
Wobei Object Generator ein Netzwerk ist, das am Eingang einen Objektbeschreibungsvektor empfängt und gibt $$$O$- das Bild (einer bestimmten Standardgröße) des Objekts und die Maske der undurchsichtigen Pixel (Opazitätsmaske).
Compositor - empfängt das Eingabebild aller Objekte, Masken, Positionen, Skalierungen und Tiefen und bildet das Ausgabebild, das dem Original ähnlich sein sollte.

Was ist der Unterschied zwischen unserem Ansatz und VAE?

Es scheint, dass wir einen Auto-Encoder mit der gleichen Architektur wie die Autoren des Artikels Räumlich invariante unbeaufsichtigte Objekterkennung mit Faltungs-Neuronalen Netzen verwenden möchten. Die Frage ist also, was der Unterschied ist. Sowohl dort als auch dort Autoencoder, nur in der zweiten Version ist es Variation.

Aus theoretischer Sicht ist der Unterschied sehr groß. VAE ist ein generatives Modell und hat die Aufgabe, zwei Verteilungen (erste und generierte Bilder) so ähnlich wie möglich zu gestalten. Im Allgemeinen übernimmt VAE keine Garantie dafür, dass das aus der „Beschreibung“ eines aus dem Originalbild erzeugten Objekts erzeugte Bild dem Original zumindest geringfügig ähnlich ist. Übrigens sprechen die Autoren von VAE Auto-Encoding Variational Bayes selbst darüber. Warum funktioniert es immer noch? Ich denke, dass die ausgewählte Architektur der neuronalen Netze und die „Beschreibung“ dazu beitragen, die gegenseitige Information des Bildes und der „Beschreibung“ zu verbessern, aber ich konnte keine mathematischen Beweise für diese Hypothese finden. Eine Frage für die Leser, kann jemand in der Lage sein, die Ergebnisse der Autoren zu erklären - ihr restauriertes Bild ist dem Original sehr ähnlich, warum?

Darüber hinaus zwingt die Verwendung von VAE die Autoren, die Verteilung von „Beschreibungen“ anzugeben, und die Methode zur Maximierung der gegenseitigen Information macht keine Annahmen darüber. Was uns zusätzliche Freiheit gibt, können wir beispielsweise versuchen, Vektoren auf einem bereits trainierten Modell zu gruppieren $$$A$Beschreibungen und Aussehen - vielleicht lernt ein solches System die Klassen von Objekten? Es sollte beachtet werden, dass ein solches Clustering unter Verwendung von VAE keinen Sinn ergibt. Beispielsweise verwenden die Autoren des Artikels eine Gaußsche Verteilung für diese Vektoren.

Die Experimente

Leider nimmt die Arbeit jetzt sehr viel Zeit in Anspruch und es ist nicht möglich, sie in akzeptabler Zeit abzuschließen. Wenn jemand mehrere tausend Codezeilen schreiben, Hunderte von Modellen für maschinelles Lernen trainieren und viele interessante Experimente durchführen möchte, einfach weil er (oder sie) Spaß daran hat, werde ich mich gerne zusammenschließen. Schreiben Sie in einem persönlichen.

Das Feld für Experimente ist hier sehr breit. Ich habe vor, zunächst den klassischen Auto-Encoder (deterministische Zuordnung von Bildern zu Beschreibungen und eine inverse Gauß-Verteilung) zu trainieren und zu sehen, was er lernt. In den ersten Experimenten wird es ausreichen, den von den Jungs von Facebook beschriebenen Komponisten zu verwenden, aber ich denke, dass es in Zukunft sehr interessant sein wird, mit verschiedenen Komponisten zu spielen, und es ist möglich, sie auch lernbar zu machen. Vergleichen Sie verschiedene Regularisierer: ohne, Sparse usw. Vergleichen Sie die Verwendung von Feedforward- und rekursiven Modellen. Verwenden Sie dann erweiterte Verteilungsmodelle für die inverse Verteilung, z. B. eine solche Dichteschätzung mit Real NVP . Sehen Sie, wie besser oder schlechter es mit flexibleren Modellen wird. Sehen Sie, was passieren wird, wenn die Anzeige von Bildern in Beschreibungen nicht deterministisch ist (generiert aus einer bedingten Verteilung). Versuchen Sie schließlich, verschiedene Clustering-Methoden auf Beschreibungsvektoren anzuwenden $$$A$und zu verstehen, ob ein solches System Objektklassen lernen kann.

Vor allem aber möchte ich die Qualität des Modells anhand der Maximierung der gegenseitigen Information und des Modells mit VAE vergleichen.