👨‍⚕️ 👩🏽‍🤝‍👨🏼 🐟 Hilbert, Lebesgue ... und die Leere 🤷🏿 🚻 🤵🏻

Unter dem Schnitt wird die Frage untersucht, wie ein guter mehrdimensionaler Indexierungsalgorithmus angeordnet werden sollte. Überraschenderweise gibt es nicht so viele Möglichkeiten.

Eindimensionale Indizes, B-Bäume

Das Maß für den Erfolg des Suchalgorithmus wird als 2 Fakten betrachtet -

Die Feststellung des Vorhandenseins oder Nichtvorhandenseins eines Ergebnisses erfolgt für die logarithmische (in Bezug auf die Größe des Index) Anzahl der Lesevorgänge von Platten-Seiten
Die Kosten für die Ausgabe eines Ergebnisses sind proportional zu seinem Volumen

In diesem Sinne sind B-Bäume recht erfolgreich und der Grund dafür kann als Verwendung eines ausgeglichenen Baumes angesehen werden. Die Einfachheit des Algorithmus beruht auf der Eindimensionalität des Schlüsselraums. Wenn erforderlich, teilen Sie die Seite, es reicht aus, die Hälfte der sortierten Elemente dieser Seite zu teilen. Im Allgemeinen geteilt durch die Anzahl der Elemente, obwohl dies nicht erforderlich ist.

Weil Wenn die Seiten des Baums auf einer Platte gespeichert sind, kann gesagt werden, dass der B-Baum die Fähigkeit hat, einen eindimensionalen Schlüsselraum sehr effizient in einen eindimensionalen Plattenraum umzuwandeln.

Wenn Sie einen Baum mit mehr oder weniger „richtiger Einfügung“ füllen, und dies ist ein ziemlich häufiger Fall, werden Seiten in der Reihenfolge des Wachstums des Schlüssels von Zeit zu Zeit im Wechsel mit höheren Seiten generiert. Es besteht eine gute Chance, dass sie sich auch auf der Festplatte befinden. Auf diese Weise wird ohne großen Aufwand eine hohe Datenlokalität erreicht - Daten mit einem nahe Wert befinden sich irgendwo in der Nähe und auf der Festplatte.

Natürlich werden beim Einfügen von Werten in zufälliger Reihenfolge die Schlüssel und Seiten zufällig generiert, wodurch die sogenannten Indexfragmentierung. Es gibt auch Anti-Fragmentierungs-Tools, die die Datenlokalität wiederherstellen.

Es scheint, dass in unserer Zeit der RAID- und SSD-Festplatten die Reihenfolge des Lesens von der Festplatte keine Rolle spielt. Vielmehr hat es nicht die gleiche Bedeutung wie zuvor. Es gibt keine physische Weiterleitung der Köpfe in der SSD, so dass die zufällige Lesegeschwindigkeit im Vergleich zum soliden Lesen wie bei einer Festplatte nicht hunderte Male abfällt. Und nur einmal alle 10 oder mehr .

Denken Sie daran, dass B-Bäume 1970 im Zeitalter der Magnetbänder und Trommeln auftauchten. Wenn der Unterschied in der Direktzugriffsgeschwindigkeit für das erwähnte Band und die Trommel viel dramatischer war als im Vergleich zu HDD und SSD.

Darüber hinaus spielt auch das 10-fache eine Rolle. Und diese 10-fachen beinhalten nicht nur die physischen Merkmale der SSD, sondern auch den grundlegenden Punkt - die Vorhersagbarkeit des Leserverhaltens. Wenn der Leser sehr wahrscheinlich nach dem nächsten Block für diesen Block fragt, ist es sinnvoll, ihn unter der Annahme proaktiv herunterzuladen. Und wenn das Verhalten chaotisch ist, sind alle Vorhersageversuche bedeutungslos und sogar schädlich.

Mehrdimensionale Indizierung

Weiter werden wir uns mit dem Index zweidimensionaler Punkte (X, Y) befassen, einfach weil es bequem und intuitiv ist, mit ihnen zu arbeiten. Aber die Probleme sind im Grunde die gleichen.

Eine einfache, „nicht anspruchsvolle“ Option mit getrennten Indizes für X und Y entspricht nicht unserem Erfolgskriterium. Es gibt nicht die logarithmischen Kosten für das Erhalten des ersten Punktes. Um die Frage zu beantworten, müssen wir überhaupt etwas im gewünschten Ausmaß tun

Führen Sie eine Suche im Index X durch und erhalten Sie alle Bezeichner aus dem X-Intervall-Bereich
ähnlich für Y.
schneiden diese beiden Sätze von Bezeichnern

Bereits der erste Punkt hängt von der Größe des Umfangs ab und garantiert nicht den Logarithmus.

Um „erfolgreich“ zu sein, muss ein mehrdimensionaler Index als mehr oder weniger ausgeglichener Baum angeordnet werden. Diese Aussage mag kontrovers erscheinen. Aber das Erfordernis einer logarithmischen Suche diktiert uns genau ein solches Gerät. Warum nicht zwei oder mehr Bäume? Bereits als die "ungekünstelte" und ungeeignete Option mit zwei Bäumen angesehen. Vielleicht gibt es geeignete. Aber zwei Bäume - das sind doppelt so viele (einschließlich gleichzeitiger) Sperren, doppelt so viel Kosten und deutlich höhere Chancen, einen Deadlock zu erwischen. Wenn Sie mit einem Baum auskommen können, sollten Sie ihn auf jeden Fall verwenden.

Angesichts all dessen ist der Wunsch, das sehr erfolgreiche B-Tree-Erlebnis als Grundlage für die Arbeit mit zweidimensionalen Daten zu verwenden und es zu „verallgemeinern“.

Also erschien der R-Baum.

R-Baum

Der R-Baum ist wie folgt angeordnet:
Anfangs haben wir eine leere Seite, fügen Sie einfach Daten (Punkte) hinzu.
Aber hier ist die Seite voll und muss geteilt werden.
Im B-Baum sind die Seitenelemente auf natürliche Weise angeordnet, sodass die Frage lautet, wie viel geschnitten werden soll. Es gibt keine natürliche Ordnung im R-Baum. Es gibt zwei Möglichkeiten:

Ordnung bringen, d.h. Führen Sie eine Funktion ein, die basierend auf X & Y einen Wert ausgibt, nach dem die Seitenelemente geordnet und entsprechend unterteilt werden. In diesem Fall degeneriert der gesamte Index zu einem regulären B-Baum, der aus den Werten der angegebenen Funktion aufgebaut ist. Zusätzlich zu den offensichtlichen Pluspunkten gibt es eine große Frage: Nun, wir haben indiziert, aber wie soll man aussehen? Dazu später mehr. Betrachten Sie zunächst die zweite Option.
Teilen Sie die Seite durch räumliche Kriterien. Zu diesem Zweck sollte jeder Seite die Ausdehnung der darauf / darunter befindlichen Elemente zugewiesen werden. Das heißt, Die Stammseite hat die Ausdehnung der gesamten Ebene. Beim Teilen werden zwei (oder mehr) Seiten generiert, deren Umfang im Umfang der übergeordneten Seite enthalten ist (für die Suche).

Es gibt reine Unsicherheit. Wie genau teilt man die Seite? Horizontal oder vertikal? Von der Hälfte der Fläche oder der Hälfte der Elemente ausgehen? Was aber, wenn die Punkte zwei Cluster bilden, Sie sie aber nur durch eine diagonale Linie trennen können? Und wenn es drei Cluster gibt?

Das bloße Vorhandensein solcher Fragen zeigt an, dass der R-Baum kein Algorithmus ist. Dies ist eine Reihe von Heuristiken, zumindest zum Teilen einer Seite während des Einfügens, zum Zusammenführen von Seiten während des Löschens / Änderns, zur Vorverarbeitung für das Einfügen in großen Mengen.

Bei der Heuristik wird ein bestimmter Baum auf einen bestimmten Datentyp spezialisiert. Das heißt, Bei Datensätzen einer bestimmten Art irrt sie seltener. „Heuristiken können nicht völlig falsch sein, weil In diesem Fall wäre es ein Algorithmus. “©.

Was bedeutet heuristischer Fehler in diesem Zusammenhang? Zum Beispiel, dass die Seite erfolglos geteilt / zusammengeführt wird und die Seiten beginnen, sich teilweise zu überlappen. Wenn der Suchumfang plötzlich auf den Überlappungsbereich der Seiten fällt, sind die Kosten für die Suche bereits nicht ganz logarithmisch. Mit der Zeit sammelt sich beim Einfügen / Löschen die Anzahl der Fehler an und die Leistung des Baums beginnt sich zu verschlechtern.

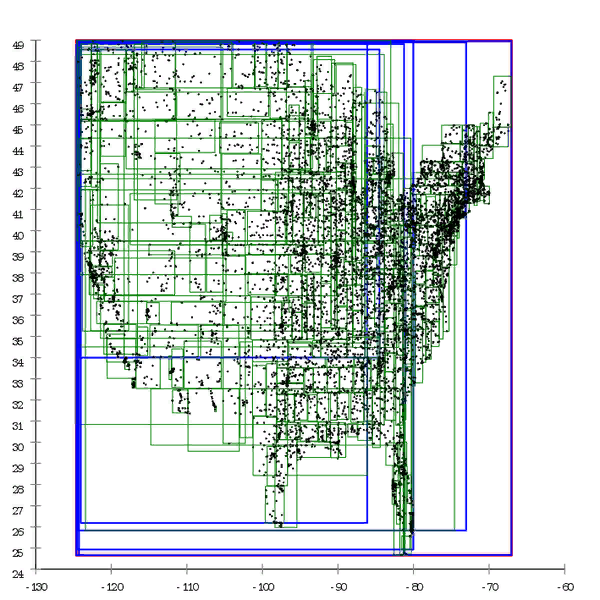Abbildung 1 Hier ist ein Beispiel für einen R * -Baum, der auf natürliche Weise erstellt wurde.

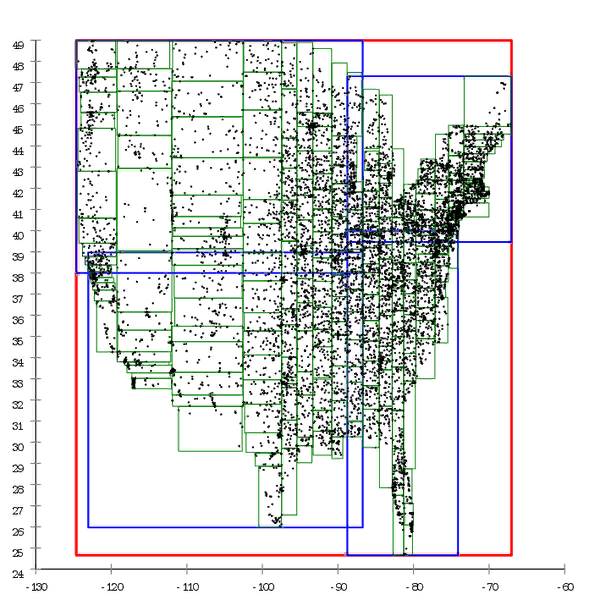Abbildung 2 Und hier wird derselbe Datensatz vorverarbeitet und der Baum durch Masseneinfügung erstellt

Wir können sagen, dass sich der B-Baum im Laufe der Zeit ebenfalls verschlechtert, aber dies ist eine etwas andere Verschlechterung. Die Leistung des B-Baums sinkt aufgrund der Tatsache, dass seine Seiten nicht hintereinander liegen. Dies kann leicht durch "Begradigen" des Baumes behandelt werden - Defragmentierung. Im Fall eines R-Baums ist es nicht so einfach, ihn loszuwerden. Die Struktur des Baums selbst ist "Kurve", um die Situation zu korrigieren. Er muss vollständig neu aufgebaut werden.

Verallgemeinerungen des R-Baums auf mehrdimensionale Räume sind nicht offensichtlich. Beim Teilen von Seiten haben wir beispielsweise den Umfang der untergeordneten Seiten minimiert. Was ist im dreidimensionalen Fall zu minimieren? Volumen oder Oberfläche? Und im achtdimensionalen Fall? Der gesunde Menschenverstand ist kein Berater mehr.

Der indizierte Raum kann durchaus nicht isotrop sein. Warum nicht nicht nur Punkte, sondern auch deren zeitliche Positionen indizieren, d.h. (X, Y, t). In diesem Fall sind beispielsweise Heuristiken, die auf dem Umfang basieren, seitdem bedeutungslos stapelt die Länge in Zeitintervallen.

Der allgemeine Eindruck des R-Baumes ist so etwas wie Krustentiere mit Kiemenfüßen . Diese haben ihre eigene ökologische Nische, in der es schwierig ist, mit ihnen zu konkurrieren. Im allgemeinen Fall haben sie jedoch keine Chance im Wettbewerb mit weiter entwickelten Tieren.

Quad-Baum

In einem Quadtree hat jede Nicht-Blattseite genau vier Nachkommen, die ihren Raum gleichmäßig in Quadranten aufteilen.

Abbildung 3 Beispiel eines konstruierten Quad-Baums

Dies ist kein gutes Datenbankdesign.

Jede Seite schränkt den Suchraum für jede Koordinate nur zweimal ein. Ja, dies liefert die logarithmische Komplexität der Suche, aber dies ist der Logarithmus zur Basis 2, nicht die Anzahl der Elemente auf der Seite (sogar 100) wie in einem B-Baum.
Jede Seite ist klein, aber dahinter müssen Sie noch auf die Festplatte gehen.
Die Tiefe des Quad-Baums muss begrenzt sein, sonst wirkt sich sein Ungleichgewicht auf die Leistung aus. Infolgedessen kann sich bei stark gruppierten Daten (z. B. Häusern auf einer Karte - es gibt viele Städte in Städten, wenige in Feldern) eine große Datenmenge auf Blattseiten ansammeln. Ein Index von einem exakten wird blockartig und erfordert eine Nachbearbeitung.

Eine schlecht ausgewählte Gittergröße (Baumtiefe) kann die Leistung beeinträchtigen. Trotzdem möchte ich, dass die Leistung des Algorithmus nicht kritisch vom menschlichen Faktor abhängt.
Die Platzkosten für die Speicherung eines Punktes sind recht hoch.

Raumnummerierung

Es bleibt die zuvor zurückgestellte Version mit einer Funktion zu betrachten, die basierend auf einem mehrdimensionalen Schlüssel den Wert für das Schreiben in einen regulären B-Baum berechnet.

Die Konstruktion eines solchen Index ist offensichtlich, und der Index selbst hat alle Vorteile des B-Baums. Die Frage ist nur, ob dieser Index für eine effektive Suche verwendet werden kann.

Es gibt eine große Anzahl solcher Funktionen, es kann davon ausgegangen werden, dass es unter ihnen eine kleine Anzahl von "gut", eine große Anzahl von "schlecht" und eine große Anzahl von "einfach schrecklich" gibt.

Es ist nicht schwierig, eine schreckliche Funktion zu finden - wir serialisieren den Schlüssel in eine Zeichenfolge, betrachten MD5 daraus und erhalten einen Wert, der für unsere Zwecke völlig nutzlos ist.

Und wie geht man mit dem Guten um? Es wurde bereits gesagt, dass ein nützlicher Index die "Lokalität" von Daten bereitstellt - Punkte, die sich im Raum befinden und beim Speichern auf der Festplatte häufig nahe beieinander liegen. In Bezug auf die gewünschte Funktion bedeutet dies, dass für räumlich nahe Punkte enge Werte erhalten werden.

Im Index werden die berechneten Werte auf den "physischen" Seiten in der Reihenfolge ihrer Werte angezeigt. Unter dem Gesichtspunkt des „physischen Sinns“ sollte der Suchumfang so wenige physische Indexseiten wie möglich betreffen. Was ist im Allgemeinen offensichtlich. Unter diesem Gesichtspunkt sind die Nummerierungskurven, die die Daten "ziehen", "schlecht". Und diejenigen, die „in einem Ball verwirren“ - näher am „Guten“.

Naive Nummerierung

Ein Versuch, ein Segment in ein Quadrat (Hyperwürfel) zu quetschen, während er in der Logik des eindimensionalen Raums bleibt, d.h. in Stücke schneiden und das Quadrat mit diesen Stücken füllen. Das kann sein

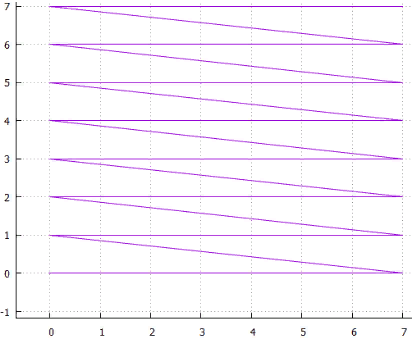4-Zeilen-Scan

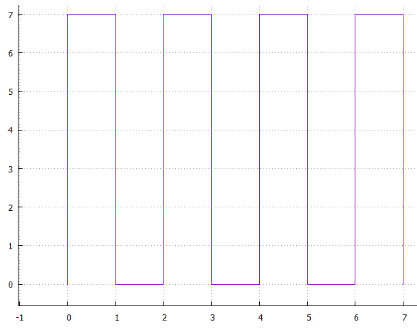5 interlaced

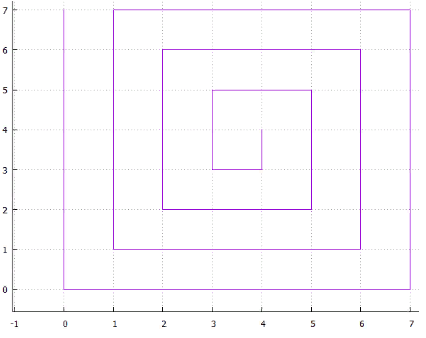Abb.6 Spirale

oder ... Sie können sich viele Optionen einfallen lassen, die alle zwei Nachteile haben

Mehrdeutigkeit zum Beispiel: Warum ist die Spirale im Uhrzeigersinn und nicht dagegen gewellt, oder warum erfolgt der horizontale Scan zuerst entlang X und dann entlang Y.
das Vorhandensein langer gerader Teile, die die Verwendung einer solchen Methode für die mehrdimensionale Indizierung unwirksam machen (großer Seitenumfang)

Direktzugriffsfunktionen

Wenn der Hauptanspruch auf "naive" Methoden darin besteht, dass sie sehr langgestreckte Seiten erzeugen, generieren wir die "richtigen" Seiten selbst.

Die Idee ist einfach: Lassen Sie den Raum extern in Blöcke unterteilen, weisen Sie jedem Block eine Kennung zu, und dies ist der Schlüssel für den räumlichen Index.

Lassen Sie die X & Y-Koordinaten 16-Bit sein (zur Verdeutlichung)
Wir werden den Raum mit quadratischen Blöcken der Größe 1024X1024 abdecken
Vergröbern Sie die Koordinaten, verschieben Sie sie um 10 Bit nach rechts
und erhalten Sie die Seiten-ID, kleben Sie die Bits von X & Y. In der Kennung sind die unteren 6 Ziffern die ältesten von X, die nächsten 6 Ziffern die ältesten von Y.

Es ist leicht zu erkennen, dass die Blöcke einen Zeilenscan bilden. Um Daten für den Suchbereich zu finden, müssen Sie daher für jede Blockreihe, auf die dieser Bereich gelegt wird, im Index suchen / lesen. Im Allgemeinen funktioniert diese Methode hervorragend, obwohl sie mehrere Nachteile hat.

Wenn Sie einen Index erstellen, müssen Sie die optimale Blockgröße auswählen, was völlig offensichtlich ist
Wenn der Block erheblich größer als eine typische Abfrage ist, ist die Suche seitdem ineffizient müssen zu viel lesen und filtern (Nachbearbeitung)
Wenn der Block erheblich kleiner als eine typische Abfrage ist, ist die Suche seitdem ineffizient müssen viele Abfragen Zeile für Zeile durchführen
Wenn der Block im Durchschnitt zu viele oder zu wenig Daten enthält, ist die Suche ineffektiv
Wenn die Daten gruppiert sind (z. B. zu Hause auf der Karte), wird die Suche nicht überall wirksam
Wenn der Datensatz gewachsen ist, kann sich herausstellen, dass die Blockgröße nicht mehr optimal ist.

Teilweise werden diese Probleme durch den Bau mehrstufiger Blöcke gelöst. Für das gleiche Beispiel:

will immer noch 1024X1024 Blöcke
Aber jetzt werden wir immer noch Blöcke der obersten Ebene der unteren Blöcke der Größe 8X8 haben
Die Taste ist wie folgt angeordnet (von niedrig nach hoch):
3 Ziffern - Ziffern 10 ... 12 X-Koordinaten
3 Ziffern - Ziffern 10 ... 12 Y-Koordinaten
3 Ziffern - Ziffern 13 ... 15 X-Koordinaten
3 Ziffern - Ziffern 13 ... 15 Y-Koordinaten

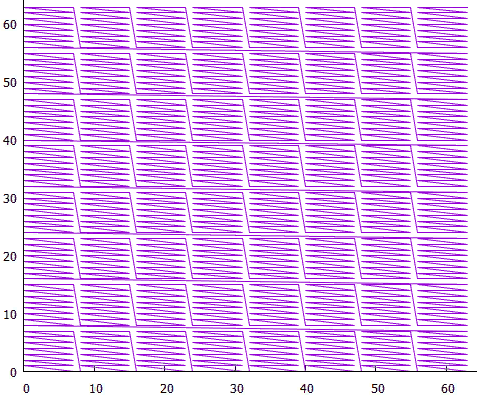7 Low-Level-Blöcke bilden High-Level-Blöcke

Bei großen Ausmaßen müssen Sie nicht mehr eine große Anzahl kleiner Blöcke lesen. Dies erfolgt auf Kosten von Blöcken auf hoher Ebene.

Interessanterweise war es möglich, die Koordinaten nicht aufzurauen, sondern auf die gleiche Weise in den Schlüssel zu drücken. In diesem Fall wäre eine Nachfilterung günstiger, weil würde beim Lesen des Index auftreten.

Räumliche GRID-Indizes sind in MS SQL auf ähnliche Weise angeordnet, wobei bis zu 4 Blockebenen zulässig sind.

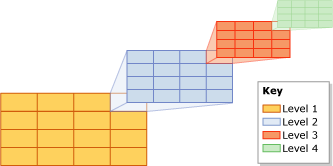Abb.8 GRID-Index

Eine weitere interessante Möglichkeit der direkten Indizierung besteht darin, einen Quad-Baum für die externe Aufteilung des Raums zu verwenden.

Der Quad-Baum ist insofern nützlich, als er sich seitdem an die Dichte von Objekten anpassen kann Wenn der Knoten überläuft, wird er aufgeteilt. Wenn die Dichte der Objekte hoch ist, werden die Blöcke daher klein und umgekehrt. Dies reduziert die Anzahl leerer Indexaufrufe.

Der Quad-Baum ist zwar eine unbequeme Konstruktion für den schnellen Wiederaufbau, es ist jedoch von Vorteil, dies von Zeit zu Zeit zu tun.

Wenn Sie einen Quad-Baum neu erstellen , müssen Sie den Index nicht neu erstellen, wenn die Blöcke durch den Morton-Code identifiziert und Objekte damit codiert werden. Hier ist der Trick: Wenn die Koordinaten des Punkts mit einem Morton-Code codiert sind, ist die Seitenkennung ein Präfix in diesem Code. Bei der Suche nach Seitendaten werden alle Schlüssel ausgewählt, die im Bereich von [Präfix] 00 ... 00B bis [Präfix] 11 ... 11B liegen. Wenn die Seite geteilt wird, bedeutet dies, dass nur das Präfix ihrer Nachkommen verlängert wurde.

Selbstähnliche Funktionen

Das erste, was mir bei der Erwähnung selbstähnlicher Funktionen einfällt, sind „Kurvenfeger“. "Eine auffällige Kurve ist eine kontinuierliche Abbildung, deren Domäne das Einheitensegment [0, 1] und deren Domäne der euklidische (streng topologische) Raum ist." Ein Beispiel ist die Peano-Kurve.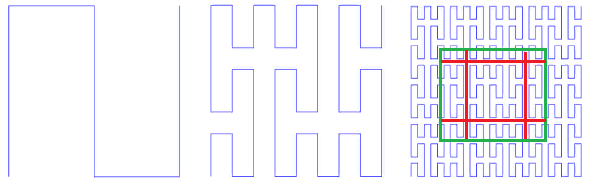

Abb. 9 erste Iterationen der Peano-Kurve

In der unteren linken Ecke befindet sich der Anfang des Definitionsbereichs (und der Nullwert der Funktion), in der oberen rechten Ecke das Ende (und 1). Jedes Mal, wenn wir einen Schritt verschieben, addieren Sie 1 / (N * N) zum Wert (vorausgesetzt, dass N - Grad 3 natürlich). Infolgedessen erreicht der Wert in der oberen rechten Ecke 1. Wenn wir bei jedem Schritt einen hinzufügen, nummeriert eine solche Funktion einfach das quadratische Gitter nacheinander, was wir wollten.

Alle geschwungenen Kurven sind selbstähnlich. In diesem Fall ist der Simplex ein 3x3-Quadrat. Bei jeder Iteration wird jeder Punkt des Simplex zum gleichen Simplex. Um Kontinuität zu gewährleisten, müssen Sie auf Zuordnungen (Flips) zurückgreifen.

Selbstähnlichkeit ist für uns eine sehr wichtige Eigenschaft. Es gibt Hoffnung für den logarithmischen Wert der Suche. Beispielsweise liegen bei einem 3x3-Simplex alle Zahlen, die in jedem der 9 Elementarquadrate durch nachfolgende Detailiterationen erzeugt werden, innerhalb desselben Bereichs. Nur weil die Zahl der von Anfang an zurückgelegte Weg ist. Das heißt, Wenn Sie die Ausdehnung in 9 Teile teilen, kann der Inhalt jedes einzelnen durch eine Indexdurchquerung erhalten werden. Und so weiter rekursiv kann jedes der 9 Unterquadrate jedes der Quadrate durch eine einzelne Abfrage des Index erhalten werden (allerdings in einem kleineren Bereich). So kann der Suchumfang in eine kleine Anzahl quadratischer Unterabfragen unterteilt werden, die entweder vollständig oder mit Filterung (um den Umfang herum) gelesen werden. Abbildung 9 zeigt den Suchumfang in Grün, durch rote Linien in Unterabfragen unterteilt.

Selbstähnlichkeit macht die Nummerierungskurve jedoch nicht automatisch für Indexierungszwecke geeignet.

Die Kurve sollte das quadratische Gitter füllen. Wir indizieren die Werte in den Knoten des quadratischen Gitters und möchten jedes Mal nicht nach einem geeigneten Knoten auf dem Gitter suchen, beispielsweise nach einem dreieckigen. Zumindest um Rundungsprobleme zu vermeiden. Hier zum Beispiel solche (Abbildung 10)

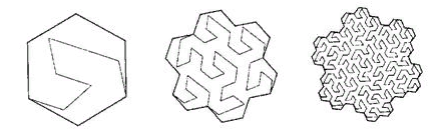
Abbildung 10 ternärer See Kokha

Die Kurve passt nicht zu uns. Obwohl es die Oberfläche perfekt „überbrückt“.
Die Kurve sollte den Raum ohne Lücken füllen ( fraktale Dimension D = 2). Hier ist es (Abb. 11):

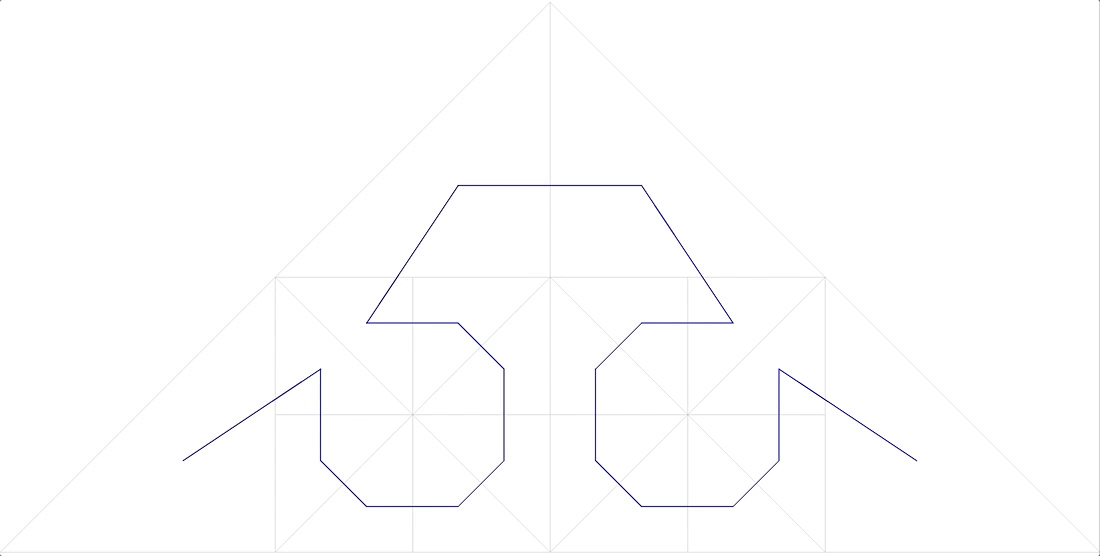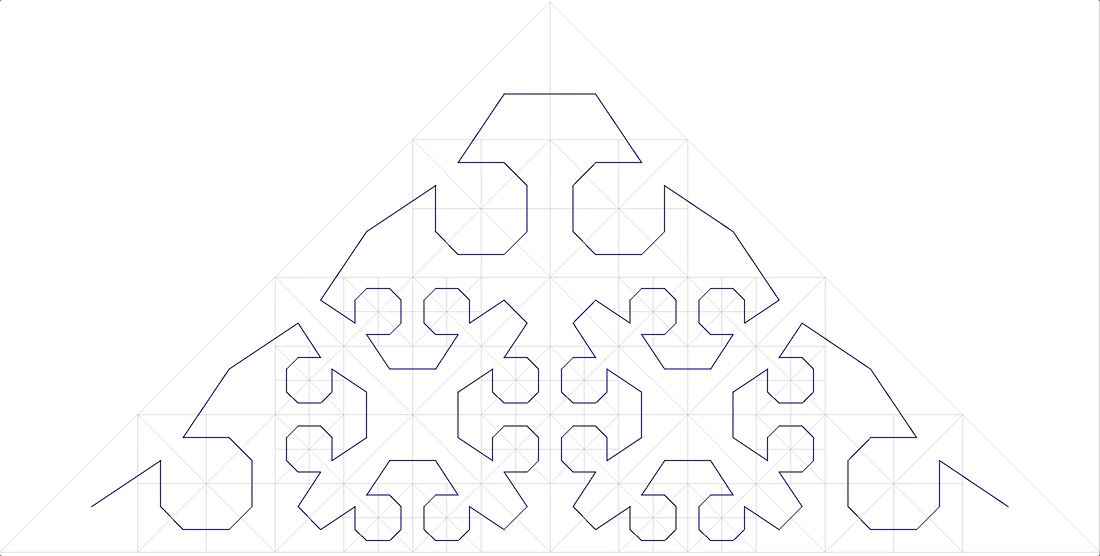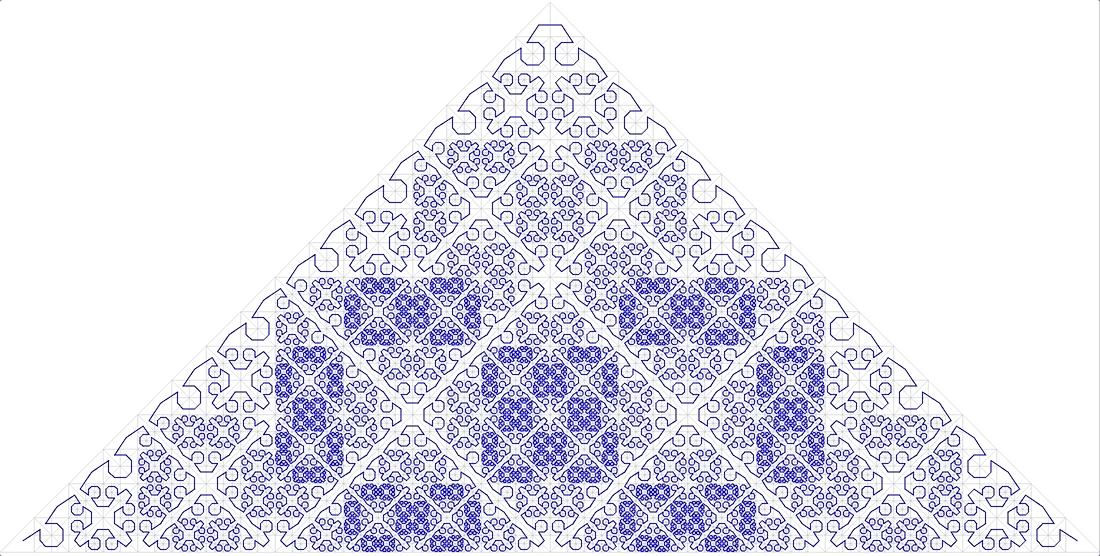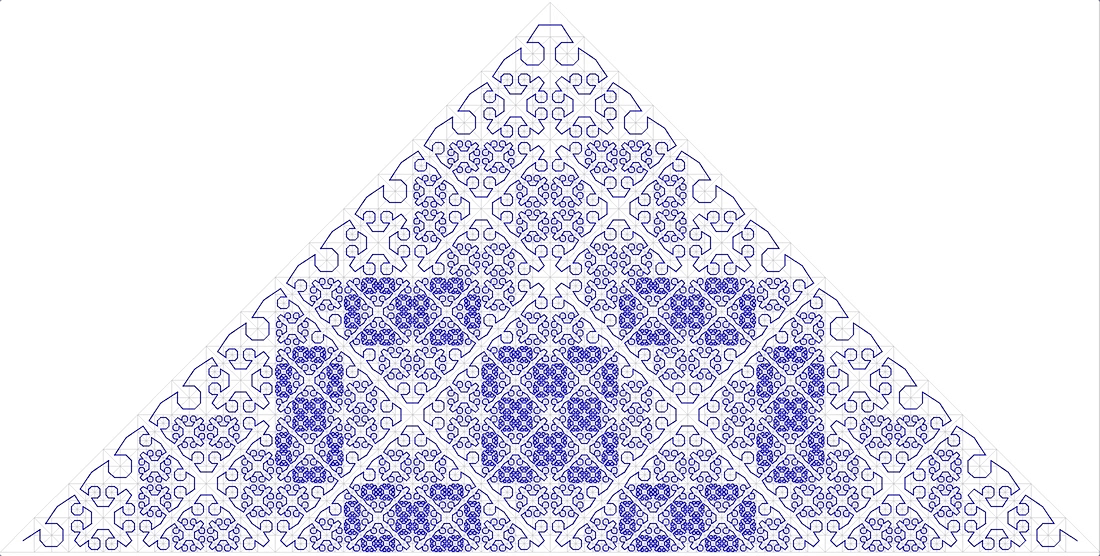
11 anonyme fraktale Kurve

passt auch nicht.
Der Wert der Nummerierungsfunktion (der von Anfang an entlang der Kurve zurückgelegte Pfad) sollte leicht zu berechnen sein. Daraus folgt, dass selbstberührende Kurven aufgrund der auftretenden Mehrdeutigkeit nicht geeignet sind, wie die Sierpinski-Kurve

Abb. 12 Sierpinski-Kurve

oder, was (für uns) dasselbe ist, " das Dreieck entlang Cesaro passieren "

FIG. 13 Cesaro-Dreieck Aus Gründen der Übersichtlichkeit wird der rechte Winkel durch 85 ° ersetzt
Die Nummerierungsfunktion sollte keine Parameter enthalten. Die Kurve sollte gleichmäßig sein (symmetrisch genau). . : ( )

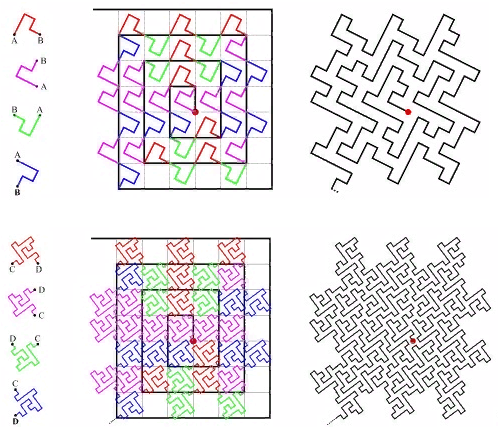
. 14 “A Plane Filling Curve for the Year 2017”

, ( ) .
, , , .

Die Isotropie ist ein weiteres wichtiges Merkmal. Es versteht sich, dass die Nummerierungsfunktion leicht auf höhere Dimensionen verallgemeinerbar sein sollte. Und es ist gut, wenn für einen N-dimensionalen Würfel alle N Projektionen auf Dimensionen (N-1) gleich sind. Dies folgt aus der Tatsache, dass wir den isotropen Raum verwenden und es seltsam wäre, wenn verschiedene Achsen in Funktionen unterschiedlich verwendet würden.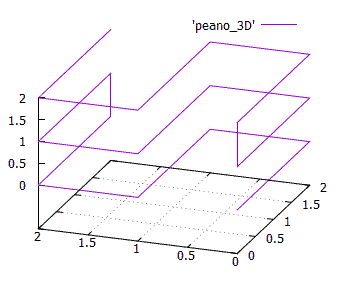

FIG. 15 Dreidimensionaler Simplex einer 3x3x3-Peano-Kurve Die

Isotropie ist keine strenge Anforderung, aber ein wichtiger Indikator für die Qualität einer Nummerierungskurve.

In Bezug auf Kontinuität .

Oben haben wir Beispiele für fortlaufende Nummerierungsfunktionen gesehen, die für unsere Zwecke nicht geeignet waren. Andererseits ist die ziemlich diskontinuierliche Zeilenabtastfunktion mit Blöcken dafür großartig (mit einigen Einschränkungen). Nicht nur das, wenn wir einen Blockindex erstellen würden, der auf kontinuierlichem Interlaced-Scannen basiert, würde dies nichts an der Leistung ändern. Denn wenn der Block vollständig gelesen wird, gibt es keinen Unterschied in der Reihenfolge, in der die Objekte empfangen werden.

Dies gilt auch für selbstähnliche Kurven.

Nennen wir die Seitengröße, den Ausdehnungsbereich aller Objekte auf der Festplattenseite
Die charakteristische Größe ist der durchschnittliche Seitenbereich
( ) , . , . — . .
— , .. .
, . , , . , , — () 3...10% () Z-.

— , .

Aus dem Gesagten folgt, dass zum Zwecke der mehrdimensionalen Indizierung nur quadratische (hyperkubische) Simplexe so oft wie nötig rekursiv angewendet werden (für eine ausreichende Detaillierung des Gitters).

Ja, es gibt andere selbstähnliche Wege, um ein quadratisches Gitter zu überbrücken. Es gibt jedoch keinen rechnerisch billigen Weg, um eine solche Transformation durchzuführen, einschließlich des Gegenteils. Vielleicht existieren solche numerischen Tricks, aber sie sind dem Autor nicht bekannt. Darüber hinaus ermöglichen quadratische Simplexe die effektive Aufteilung des Suchumfangs in Unterabfragen durch einen Schnitt entlang einer der Koordinaten . Mit einer gebrochenen Grenze zwischen Simplexen ist dies unmöglich .

Warum sind die Simplexe quadratisch und nicht rechteckig? Aus Gründen der Isotropie.

Es bleibt die Wahl der geeigneten Größe und Nummerierung innerhalb des Simplex (Bypass).

Um die Größe eines Simplex zu wählen , müssen Sie herausfinden, welche Auswirkungen dies hat. Die Anzahl der generierten Unterabfragen, die während der Suche erstellt werden müssen. Zum Beispiel wird ein Simplex 3X3 einer Peano-Kurve in 3 Unterabfragen mit fortlaufenden Intervallen von Zahlen geschnitten, zuerst in X und dann jeweils in 3 Teile in Y. Als Ergebnis kehren wir zur nächsten Stufe der Rekursion zurück. Wenn wir einen ähnlichen (Interlaced) Simplex 5X5 hätten, müsste er in 5 Teile geschnitten werden. Oder in ungleiche Teile (z. B. 2 + 3), was seltsam ist.

Es erinnert in gewisser Weise an einen der Suchbäume - Sie können natürlich sowohl 5-Dezimal- als auch 7-Dezimal-Bäume verwenden, aber in der Praxis werden nur binäre Bäume verwendet. Dreifaltigkeitsbäumehaben ihre eigene enge Nische für die Suche nach Präfix. Und das ist nicht genau das, was intuitiv als ternäre Bäume verstanden wird.

Dies erklärt sich aus der Effizienz. In einem ternären Knoten müssten zwei Vergleiche durchgeführt werden, um einen Nachkommen auszuwählen. In einem Binärbaum entspricht dies einer Auswahl unter 4 Optionen. Selbst kürzere Baumtiefen blockieren nicht den Produktivitätsverlust aufgrund der erhöhten Anzahl von Vergleichen.

Wenn 3X3 effektiver wäre als 2X2, nur weil 3> 2, wäre 4X4 außerdem effektiver als 3X3 und 8X8 effektiver als 5X5. Sie können immer die passende Zweierpotenz finden, die aus mehreren Iterationen von 2X2 besteht ...

Und was wird durch den Simplex-Bypass beeinflusst ? Zunächst die Anzahl der durch die Suche generierten Unterabfragen. WeilEs ist gut, wenn Sie sich mit dem Simplex mit fortlaufenden Zahlenintervallen in Stücke schneiden können. Hier erlaubt Peano 3X3, so dass eine Iteration es in 3 Teile schneidet. Und wenn Sie einen 8x8-Simplex mit einem Schachritter nehmen (Abb. 16), besteht die einzige Möglichkeit darin, sofort 64 Elemente zu haben.

FIG. 16 Eine der Optionen zur Umgehung des 8x8-Simplex

Da wir also herausgefunden haben, dass der optimale Simplex 2x2 ist, sollten wir überlegen, welche Optionen dafür existieren.

FIG. 17 Optionen zur Umgehung eines 2x2-Simplex

Es gibt drei davon, bis zur Symmetrie, die bedingt als „Z“, „Omega“ und „Alpha“ bezeichnet werden.
Es fällt sofort auf, dass sich „Alpha“ kreuzt und daher für die binäre Aufteilung ungeeignet ist. Es müsste sofort in 4 Teile geschnitten werden. Oder 256 im 8-dimensionalen Fall.

Die Möglichkeit, einen einzelnen Algorithmus für Räume mit unterschiedlichen Dimensionen zu verwenden (was uns bei einer Kurve wie „Alpha“ entzogen ist), sieht sehr attraktiv aus. Daher werden wir in Zukunft nur die ersten beiden Optionen in Betracht ziehen.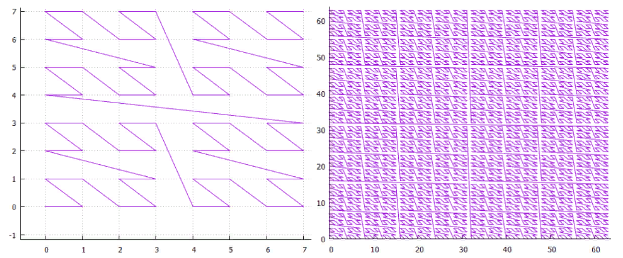

FIG. 18 Z-Kurve von

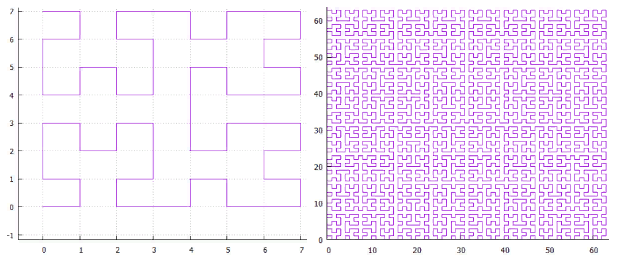FIG. 19 „Omega“ - Hilbert-Kurve.

Sobald diese Kurven eine enge Verwandtschaft haben, können sie mit einem Algorithmus verarbeitet werden. Die Hauptspezifität der Kurve ist in der Aufteilung der Unterabfrage lokalisiert.

Zuerst finden wir die Startausdehnung. Dies ist das minimale Rechteck, das die Suchausdehnung enthält und ein kontinuierliches Intervall von Schlüsselwerten enthält.
Es wird wie folgt gefunden -
- Berechnen Sie die Schlüsselwerte für den unteren linken und oberen rechten Punkt des Suchumfangs (KMin, KMax).
- ( ) KMin, KMax
- , SMin, , SMax
- . , , SMin, . .
- , , ( ).
- Z- . z- — , — ( ). , , .
- , , . ,
- , . — “ ” >= “ ” () , “ ”
  - “ ” > , ,
  - , ,
  - “ ” > , , ,
  - separater Fall "letzter Schlüssel" == Maximalwert der aktuellen Unterabfrage, separat durch Vorwärtsfahrt verarbeitet
- Teilen Sie die aktuelle Unterabfrage
  - Addiere 0 und 1 zu seinem Präfix - wir erhalten zwei neue Präfixe
  - Füllen Sie den Rest des Schlüssels 0 oder 1 aus - wir erhalten die minimalen und maximalen Werte neuer Unterabfragen
  - Wir schieben sie auf den Stapel, zuerst den, der 1, dann 0 ergänzt. Dies dient zum unidirektionalen Lesen des Index.

Auf einer Z-Kurve funktioniert das folgendermaßen:

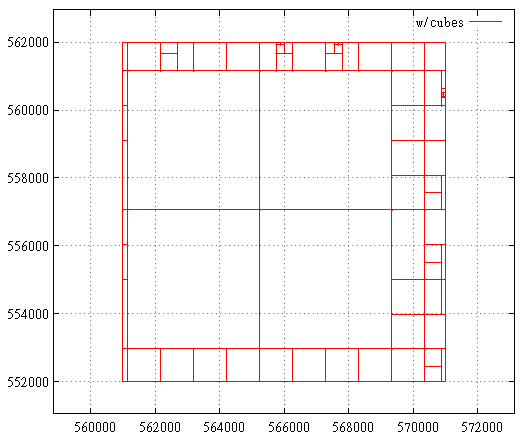FIG. 20 - Aufteilung der Unterabfragen bei Z-Kurve

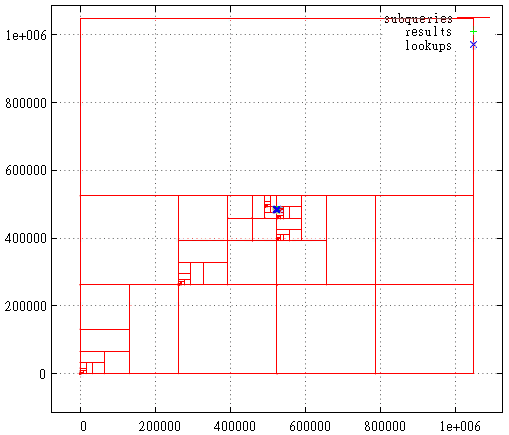FIG. 21 Hilbert-Kurve, wenn die Startausdehnung maximal ist

Hier wird die erste Stufe gezeigt - das Abschneiden der überschüssigen Schicht von maximaler Ausdehnung.

FIG. 22 Hilbert-Kurve, Suchabfragebereich

Und hier ist eine Aufschlüsselung in Unterabfragen, gefundene Punkte und Indexaufrufe im Suchabfragebereich. Dies ist aus Sicht der Hilbert-Kurve immer noch eine sehr erfolglose Anfrage. Normalerweise ist alles viel weniger blutig.

Abfragestatistiken besagen jedoch, dass ein zweidimensionaler Index, der auf einer Hilbert-Kurve basiert, (ungefähr) auf denselben Daten durchschnittlich 5% weniger Festplattenseiten liest, aber halb langsamer arbeitet. Die Verlangsamung wird auch durch die Tatsache verursacht, dass die Berechnung selbst (direkt und umgekehrt) dieser Kurve viel schwieriger ist - 2000 Prozessortakte für Hilbert im Vergleich zu 50 für die Z-Kurve.

Wenn die Hilbert-Kurve nicht mehr unterstützt wird, könnte der Algorithmus vereinfacht werden. Auf den ersten Blick ist eine solche Verlangsamung nicht gerechtfertigt. Auf der anderen Seite ist dies nur ein zweidimensionaler Fall. Beispielsweise können Statistiken im 8-dimensionalen Raum oder mehr mit völlig neuen Farben funkeln. Dieses Problem muss noch geklärt werden.

PS : Die Z-Kurve wird aufgrund des Algorithmus zur Berechnung des Werts manchmal als Bit-Interleaving-Kurve bezeichnet. Die Ziffern jeder Koordinate fallen durch eins in den Schlüsselwert, was sehr technologisch ist. Schließlich können Sie die Entladungen nicht einzeln, sondern in Packungen mit 2,3 ... 8 ... Stücken verschachteln. Wenn wir nun 8 Bit nehmen, erhalten wir auf einem 32-Bit-Schlüssel ein Analogon des 4-Ebenen-GRID-Index von MS SQL. Und im Extremfall - ein Pack mit jeweils 32 Bit - ein horizontaler Scan-Algorithmus.

Ein solcher Index (natürlich nicht in Kleinbuchstaben) kann sehr effektiv sein und bei einigen Datensätzen sogar effizienter als die Z-Kurve. Leider aufgrund des Verlustes der Allgemeinheit.

PPS : Der beschriebene Index ist der Arbeit mit einem Quad-Baum sehr ähnlich. Die maximale Ausdehnung ist die Stammseite des Quad-Baums, sie hat 4 Nachkommen ... Daher kann der Algorithmus „Direktzugriffsmethoden“ zugeordnet werden.

Unterschiede sind immer noch grundlegend.

Der Quad-Baum wird nirgendwo gespeichert, er ist virtuell und in die Natur der Zahlen eingebettet. Es gibt keine Einschränkungen hinsichtlich der Tiefe des Baums. Wir erhalten Informationen über die Population der Nachkommen aus der Population des Hauptbaums. Außerdem wird der Hauptbaum einmal gelesen, wir gehen vom kleinsten zum ältesten Wert. Es ist lustig, aber die physische Struktur des B-Baums ermöglicht es, leere Abfragen zu vermeiden und die Rekursionstiefe zu begrenzen.

Eine weitere Sache - bei jeder Iteration erscheinen nur zwei Nachkommen - aus ihnen können 4 Unterabfragen generiert werden, die nicht generiert werden können, wenn keine Daten darunter sind. Im dreidimensionalen Fall würden wir über 8 Nachkommen sprechen, im 8-dimensionalen Fall über 256.

PPPS : Am Anfang dieses Artikels haben wir über die Dichotomie bei der Suche in einem mehrdimensionalen Index gesprochen. Um den logarithmischen Wert zu erhalten, muss eine endliche Ressource entweder bei der Iteration geteilt werden - entweder beim Schlüsselwertraum oder beim Suchraum. In dem vorgestellten Algorithmus ist diese Dichotomie zusammengebrochen - wir teilen gleichzeitig sowohl den Schlüssel als auch den Raum.

„Ich lebe in beiden Höfen und meine Bäume sind immer höher.“ ( C )

PPPPS : Sobald sie die Z-Kurve aufrufen, haben Sie hier die Z-Ordnung und die Bitverschachtelung sowie den Morton-Code / die Morton-Kurve. Es ist auch als Lebesgue-Kurve bekannt. Um das Gleichgewicht aufrechtzuerhalten, betitelte der Autor den Artikel, auch zu Ehren von Henry Leon Lebesgue .

PPPPPS : In der Titelillustration ist der Blick auf den Fedchenko-Gletscher einfach wunderschön und es gibt genug Leere. Tatsächlich war der Autor beeindruckt davon, wie reibungslos verschiedene Ideen und Methoden ineinander fließen und allmählich zu einem Algorithmus verschmelzen. So wie die vielen kleinen Wasserquellen, aus denen das Einzugsgebiet besteht, einen einzigen Abfluss bilden.

Hilbert, Lebesgue ... und die Leere