Zufällige Flächen verbergen die komplizierte Reihenfolge

Mathematiker haben bewiesen, dass ein zufälliger Prozess, wenn er auf eine zufällige Oberfläche angewendet wird, immer bestimmte Muster erzeugt

Im Originalartikel ist dies ein dreidimensionales Bild, das verdreht werden kann

In dem Film über die Suche nach der verlorenen Arche musste Indiana Jones nach einem geheimen Raum suchen, in dem sich die legendäre Bundeslade versteckt. Um den genauen Standort zu bestimmen, musste Indiana eine spezielle Karte finden, die nur sichtbar ist, wenn die Sonne zu einer bestimmten Tageszeit durch einen speziellen Kristall in einem bestimmten Raum scheint.

Eine ähnliche Idee - dass die wichtigsten Informationen nur mit dem genauen Zusammentreffen bestimmter Umstände offengelegt werden können - findet sich in vielen Mythen. Es kommt in der Mathematik vor, manchmal in unerwarteten Situationen. Nun haben drei Mathematiker bewiesen, dass, wenn eine bestimmte Art von Zufälligkeit sehr genau abgestimmt ist, komplizierte geometrische Formen erscheinen - wie eine Karte mit einem Schatz auf einem normalen Boden.

Diese Figuren sind wie Schachzellen, die über Gitter verteilt sind, die wiederum selbst durch einen zufälligen Prozess erzeugt werden. Man würde denken, dass wir Verwirrung stiften, wenn wir Zufälligkeit in Zufälligkeit stapeln. Es stellt sich heraus, dass, wie im Fall von Schneeflocken, wenn jede von ihnen einzigartig ist, aber gleichzeitig alle Schneeflocken, das Chaos zu einer universellen Form konvergiert - wenn sich nur herausstellt, dass die Bedingungen genau den Anforderungen entsprechen.

Wendepunkt

Jeder weiß, dass Mathematiker Formen studieren. Die meisten dieser Formen folgen deterministischen Regeln: Wenn ich Ihnen Anweisungen zum Aufbau einer Kugel gebe, erhalten Sie jedes Mal dieselbe Kugel.

Aber auch Mathematiker untersuchen die Formen, die durch zufällige Prozesse erhalten werden, wie zum Beispiel zufälliges Gehen - ein Pfad, dessen Richtung für jeden Schritt zufällig ausgewählt wird. Neben zufälligen Spaziergängen gibt es andere Arten von zufälligen geometrischen Objekten, z. B. zufällige zweidimensionale Oberflächen (stellen Sie sich eine Landschaft vor, in der Hügel und Täler zufällig verstreut sind) und zufällige Karten (eine Reihe von zufälligen Punkten, die durch Linien verbunden sind).


Zufällige Oberfläche durch Kleben von Dreiecken

Alle diese Formen unterscheiden sich voneinander. Mathematiker haben jedoch festgestellt, dass diese zufälligen Prozesse zu bestimmten kanonischen Formen konvergieren. Zum Beispiel sind alle zufälligen Spaziergänge eine Form der Brownschen Bewegung mit einem ziemlich langen Gang. In den letzten Jahren haben Mathematiker kanonische Formen und andere zufällige Prozesse entdeckt - und dafür die höchsten Auszeichnungen in ihren Bereichen erhalten.

Die neuen Erkenntnisse beziehen sich auf das Verständnis der zugrunde liegenden Eigenschaften eines anderen zufälligen Prozesses.

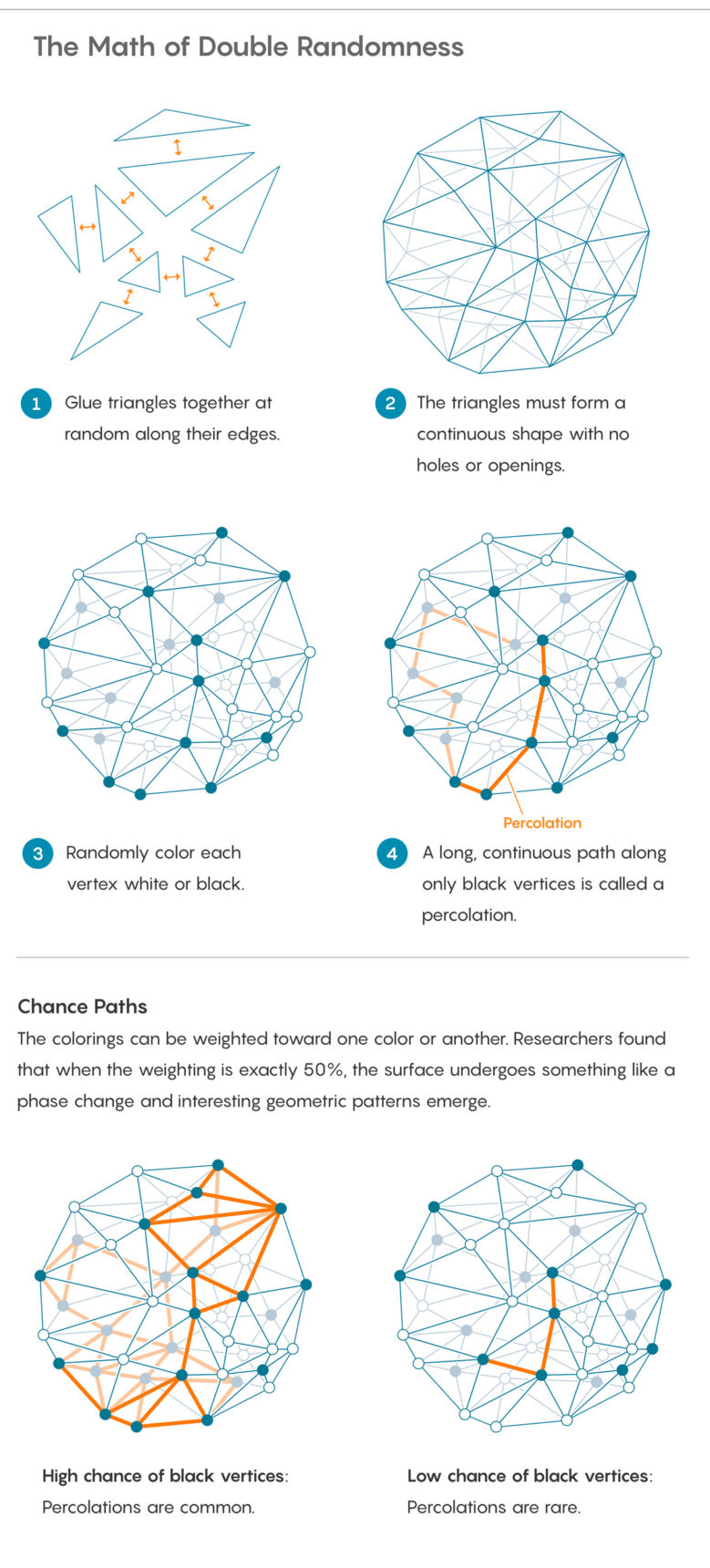
Es beginnt mit der Erstellung einer zufälligen Oberfläche. Zuerst müssen Sie die Dreiecke zusammenkleben. Dann müssen sie in irgendeiner Weise aufeinander abgestimmt werden, nur damit das resultierende Formular geschlossen wird, wie ein Paket auf einem Geschenk (hatte keine Löcher). Wenn Sie mit einer bestimmten Anzahl von Dreiecken an Ihren Händen beginnen, haben Sie viele Möglichkeiten. Einige dieser „Triangulationen“ erzeugen nahezu glatte Oberflächen, die wie eine Kugel aussehen. Die meisten von ihnen sehen rauer aus - wie extreme Oberflächen, die Gebirgszügen ähneln.

"Es wird nicht wie eine reguläre Kugel aussehen, es wird so große Spitzen haben", sagte Olivier Bernardi , Mathematiker an der Brandeis-Universität, Co-Autor der Arbeit, an der auch Nicholas Curien von der Universität Paris-Süd-XI und Gregory Mjermont von der Higher Normal School in beteiligt waren Lyon.


Olivier Bernardi, Nicholas Curien und Gregory Myermont

Myermont und ein anderer Mathematiker, Jean-Francois le Gall , haben in ihren früheren Arbeiten viele Eigenschaften dieser zufälligen Triangulationen festgestellt. Der neue Beweis geht noch weiter, indem er eine zweite Zufälligkeitsebene über die zufällige Triangulation legt.

Um eine neue Zufälligkeit hinzuzufügen, markieren Sie jeden Punkt, an dem sich die Dreiecke an den Ecken treffen - was Mathematiker einen Scheitelpunkt nennen. Färben Sie die Scheitelpunkte zufällig in Schwarz oder Weiß. Sie können dies tun, indem Sie eine Münze werfen, obwohl die Münze möglicherweise nicht ganz ehrlich ist und auf einer Seite überwiegt.

Nachdem Sie die Peaks gemalt haben, können Sie verschiedene Fragen zu dem von Ihnen erstellten Muster stellen. Eine der grundlegenden: Wie weit können Sie mit nur einem schwarzen Scheitelpunkt entlang der Oberfläche gehen? Das Bewegen entlang verbundener Eckpunkte derselben Farbe wird als Versickerung bezeichnet. Dies ist eine mathematische Methode, um ein physikalisches Phänomen mit demselben Namen zu untersuchen, wenn eine Flüssigkeit durch ein poröses Medium gelangt.

Es wird leicht zu infiltrieren sein (oder nicht), abhängig davon, wie das Gewicht der Münze verteilt ist: Wenn die Münze dazu neigt, schwarze Eckpunkte auszugeben, ist eine Infiltration fast garantiert; Wenn für die Auslieferung von Weißen eine Versickerung mit ziemlicher Sicherheit unmöglich sein wird.



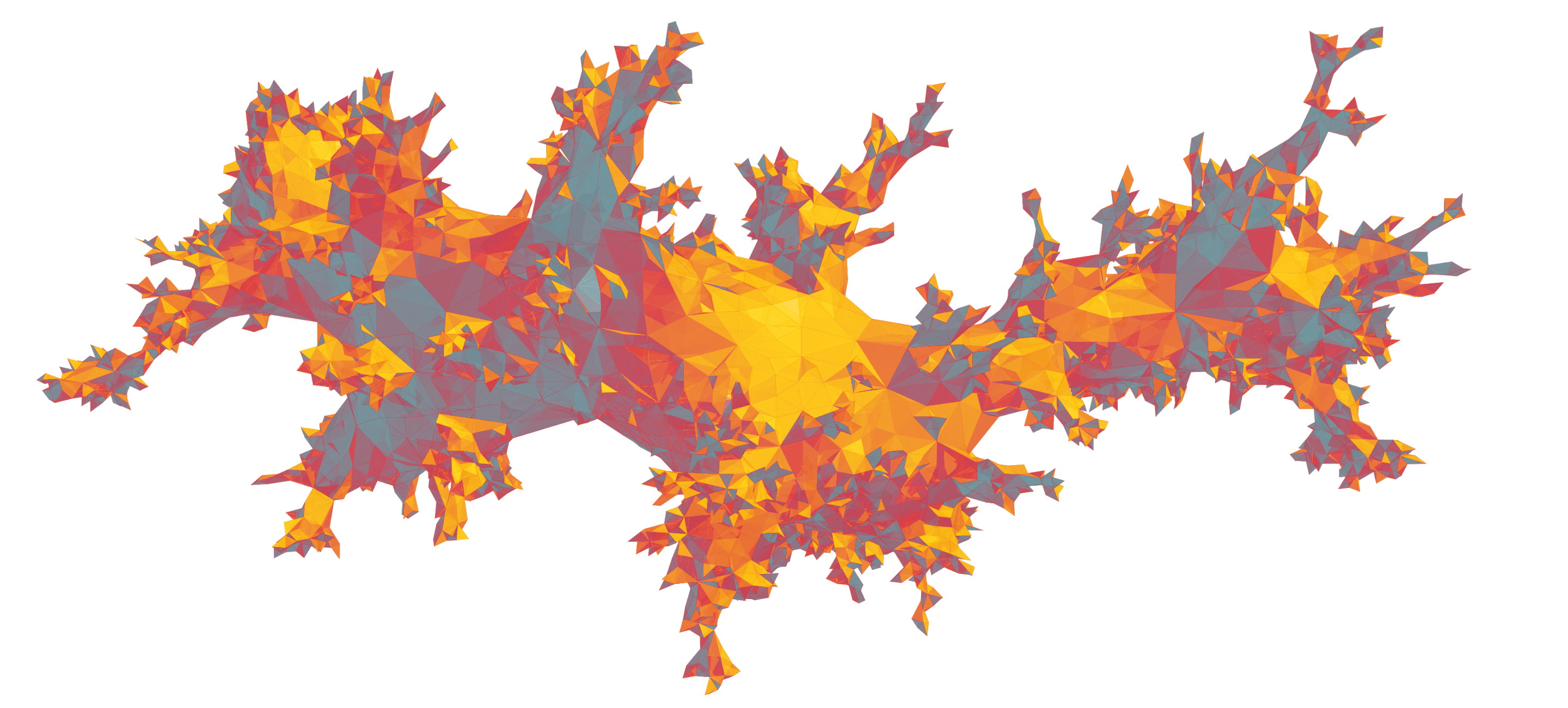
Bernardi, Curien und Myermont untersuchen Fälle, die zwischen diesen Extrema liegen - ein Wendepunkt bei der Änderung des Gewichts der Münze, wenn sich die Leckage von einem nahezu unmöglichen zu einem fast garantierten Phänomen ändert. Sie nennen diesen Punkt eine "kritische Schwelle". Dies ist ein Beispiel für einen Phasenübergang, diesen magischen Moment, in dem heißes Wasser plötzlich zu Dampf wird.

"Die kritische Schwelle bedeutet, dass sich das Verhalten meines Systems mit einem anderen Vorzeichen von dramatisch zu dramatisch ändert, wenn ich meine Parameter leicht verschiebe", sagte Curien.

Physiker sind an Phasenübergängen interessiert, da viele der wichtigsten Naturphänomene direkt am Rande auftreten. Mathematiker interessieren sich auch für Phasenübergänge, da wichtige mathematische Eigenschaften oft nur an diesen Stellen auftreten.

"Wir wissen, dass Wasser bei 100 Grad kocht und all diese verrückten Muster und Dampfformen erzeugt", sagte Scott Sheffield , Mathematiker am MIT. „Manchmal wird solch verrücktes und wildes Verhalten sehr interessant. Dieser Phasenübergang ruft uns dazu auf, ihn zu verstehen. “

In der neuen Arbeit beweisen drei Mathematiker, dass sich ein solches verrücktes Verhalten genau im Phasenübergang von Leckagen manifestiert. Sie zeigen, dass an dieser kritischen Schwelle eine geometrische Form erscheint - einzigartig und gleichzeitig universell.

Versteckte Reihenfolge im Zufall

Der erste Teil der Arbeit bestimmt, wie eine Münze so korrigiert wird, dass die Färbung der Eckpunkte auf die Schwelle zwischen Vorhandensein und Nichtvorhandensein von Versickerung fällt. Sie bestätigen die Intuition und beweisen, dass die ideale Münze der kritische Wert ist - mit einer Wahrscheinlichkeit von 50%, schwarz zu werden, und einer Wahrscheinlichkeit von 50%, weiß zu werden.

„Dies ist der erste Teil der Arbeit. Wir beweisen, dass genau die Hälfte etwas Interessantes passiert “, sagte Bernardi.


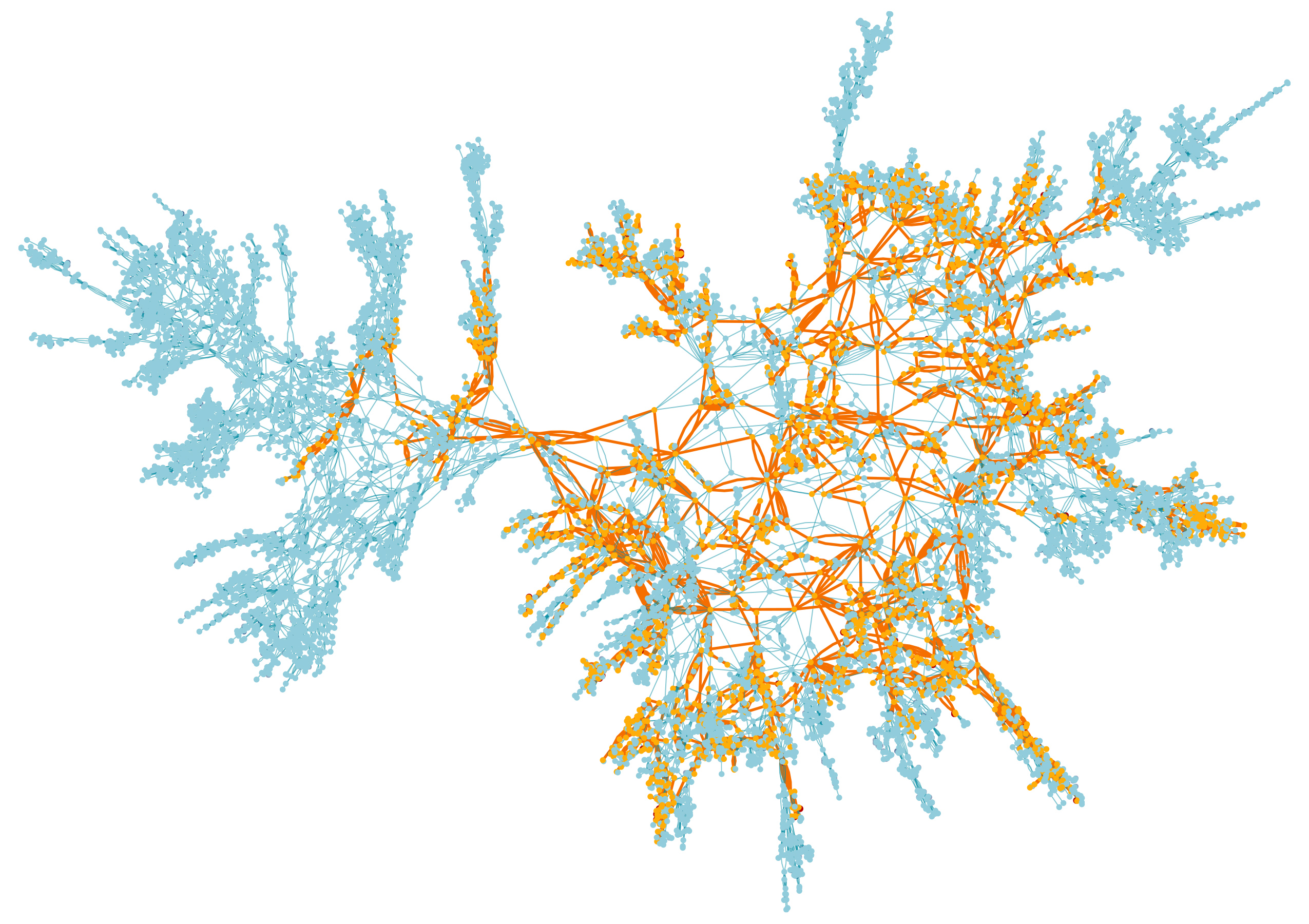Karte der Spitzen einer zufälligen Oberfläche, der größte Cluster ist orange markiert

Im zweiten Teil untersuchen wir genau das, was dort passiert. Wenn Sie die Scheitelpunkte mit einer fairen Münze in Schwarzweiß färben, erhalten Sie eine gute Balance zwischen Clustern von Schwarzweißscheitelpunkten. Cluster wachsen umeinander herum, wie Unkrautdickichte, die um einen Platz in einem bewachsenen Garten konkurrieren, und bilden komplexe geometrische Formen, die nicht erscheinen, wenn eine der Blumen zwischen den Gipfeln dominiert.

"Durch die Auswahl eines kritischen Parameters entdecken Sie große Cluster", sagte Sheffield. "Sie färben jedoch nicht das Ganze und sie sind nicht klein."

Da die Oberfläche zufällig erstellt wurde und der Vorgang des Färbens der Scheitelpunkte ebenfalls zufällig ist, unterscheidet sich ein großer Cluster auf einer Oberfläche immer von einem großen Cluster auf einer anderen. Mathematiker haben jedoch bewiesen, dass für alle Oberflächen und alle möglichen Arten, ihre Scheitelpunkte zu färben, die größten Cluster dieselben Eigenschaften haben. Das erste, was sie bewiesen haben, ist die genaue Wahrscheinlichkeitsverteilung der Größen der größten schwarzen Cluster über alle Oberflächen. Sie fanden heraus, dass am häufigsten ein Cluster einer bestimmten Zwischengröße auftritt und dass die Häufigkeit, mit der größere oder kleinere Cluster auftreten, mit der Entfernung von diesem Zwischenprodukt exponentiell zunimmt.

Sie argumentieren auch, dass alle großen Cluster auf dieselbe kanonische Form reduziert werden können, die als „stabile Karte“ bekannt ist. Die stabile Karte bezieht sich auf diese Cluster auf die gleiche Weise wie die Brownsche Bewegung zum zufälligen Gehen. Dies bedeutet, dass wenn einzelne Cluster leicht entfremdet sind - so dass jeder zufällige Schritt innerhalb des Clusters in der Geometrie der gesamten Figur weniger wahrnehmbar ist - die Cluster allmählich eine gemeinsame Form annehmen. Sie sehen aus wie Schneeflocken: Sie scheinen in der Umgebung einzigartig zu sein, aber ihre Gemeinsamkeit ist von weitem deutlich sichtbar.

"Sie fanden diese stabile Karte, die natürliche Grenze der Skalierung", sagte Sheffield.

Die Arbeit erweitert die Grenzen des Wissens über zufällige Formen und Prozesse, die Mathematiker in den letzten Jahren angesammelt haben. Es zeigt uns auch, dass genau in dem Moment, in dem das Zufallssystem am chaotischsten erscheint, eine außergewöhnliche geometrische Ordnung durch es hindurch sichtbar wird.