Es gibt zwei Männer namens "Van Eck". Die erste im Jahr 1985 zeigte der Welt, wie man Daten von einem Monitor abfängt (
Van Eck Phreaking ), für 15 US-Dollar, die zweite im Jahr 2010 entwickelte eine listige Sequenz (
Van Ecks Sequenz ). Steiler als die Einfachheit der Aufgabe dieser Sequenz können nur ihre Eigenschaften und Geheimnisse sein.
Also der Algorithmus zum Generieren von Sequenzelementen. Wir nehmen die "Startnummer", zum Beispiel "0", aus. Der nächste Term gibt an, wie viele Schritte zurück diese Nummer in der vorherigen Teilsequenz aufgetreten ist. Wenn nie, dann schreibe Null. Der nächste ist, wie viele Schritte zurück es in der vorherigen Teilsequenz Null gab, dh einen Schritt zurück. Wir schreiben die Einheit auf. Einheit eins - schreibe Null. Ups, Null traf zwei Schritte zurück. Wir schreiben zwei und so weiter ...
Für den Berichtspunkt „0“ sind die ersten 97 Mitglieder der Sequenz:
0, 0, 1, 0, 2, 0, 2, 2, 1, 6, 0, 5, 0, 2, 6, 5, 4, 0, 5, 3, 0, 3, 2, 9, 0, 4, 9, 3, 6, 14, 0, 6, 3, 5, 15, 0, 5, 3, 5, 2, 17, 0, 6, 11, 0, 3, 8, 0, 3, 3, 1, 42, 0, 5, 15, 20, 0, 4, 32, 0, 3, 11, 18, 0, 4, 7, 0, 3, 7, 3, 2, 31, 0, 6, 31, 3, 6, 3, 2, 8, 33, 0, 9, 56, 0, 3, 8, 7, 19, 0, 5, 37, 0, 3, 8, 8, 1
Grafik:
Noch mehr Zeitleiste:
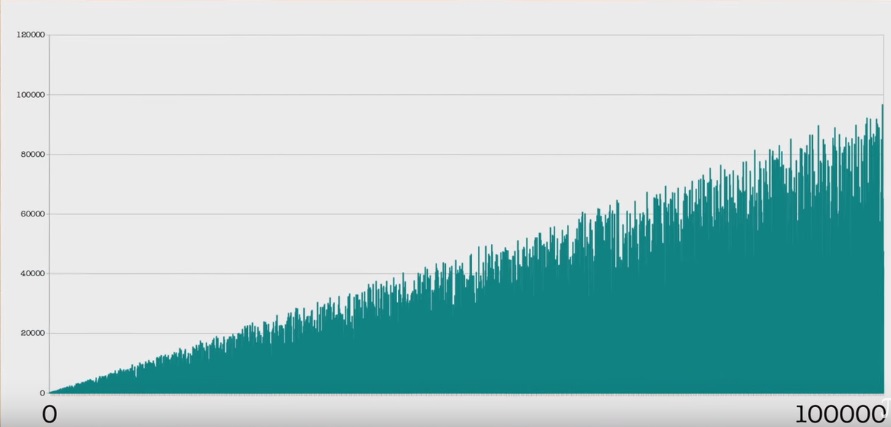
Die Eigenschaften einer Sequenz lassen sich ziemlich leicht beweisen, dass ihre maximale Laufzeit ständig zunimmt und dass sie eine unendliche Anzahl von Nullen aufweist. Oder dass es keine Perioden gibt. (Einige Sätze und Konsequenzen
hier .)
Logarithmischer Graph:
Programm in Python:
A181391 = [0] last_pos = {} for i in range(10**4): new_value = i - last_pos.get(A181391[i], i) A181391.append(new_value) last_pos[A181391[i]] = i
Für die Startnummer "1" sind die ersten hundert:
1, 0, 0, 1, 3, 0, 3, 2, 0, 3, 3, 1, 8, 0, 5, 0, 2, 9, 0, 3, 9, 3, 2, 6, 0, 6, 2, 4, 0, 4, 2, 4, 2, 2, 1, 23, 0, 8, 25, 0, 3, 19, 0, 3, 3, 1, 11, 0, 5, 34, 0, 3, 7, 0, 3, 3, 1, 11, 11, 1, 3, 5, 13, 0, 10, 0, 2, 33, 0, 3, 9, 50, 0, 4, 42, 0, 3, 7, 25, 40, 0, 5, 20, 0, 3, 8, 48, 0, 4, 15
Grafik:
Für die Startnummer "2" sind die ersten hundert:
2, 0, 0, 1, 0, 2, 5, 0, 3, 0, 2, 5, 5, 1, 10, 0, 6, 0, 2, 8, 0, 3, 13, 0, 3, 3, 1, 13, 5, 16, 0, 7, 0, 2, 15, 0, 3, 11, 0, 3, 3, 1, 15, 8, 24, 0, 7, 15, 5, 20, 0, 5, 3, 12, 0, 4, 0, 2, 24, 14, 0, 4, 6, 46, 0, 4, 4, 1, 26, 0, 5, 19, 0, 3, 21, 0, 3, 3, 1, 11, 42, 0, 6, 20, 34, 0, 4, 20, 4
Grafik:
Quellen