Das Buch "Grok Deep Learning"

Hallo habrozhiteli! Das Buch legt den Grundstein für die weitere Beherrschung der Deep-Learning-Technologie. Es beginnt mit einer Beschreibung der Grundlagen neuronaler Netze und untersucht anschließend die zusätzlichen Architekturschichten im Detail.

Das Buch wurde speziell mit der Absicht geschrieben, die niedrigstmögliche Eintrittsschwelle bereitzustellen. Sie benötigen keine Kenntnisse über lineare Algebra, numerische Methoden, konvexe Optimierungen und sogar maschinelles Lernen. Alles, was erforderlich ist, um tiefes Lernen zu verstehen, wird im Laufe der Zeit geklärt.

Wir bieten Ihnen an, sich mit der Passage "Was ist ein Deep-Learning-Rahmen?"

Gute Tools reduzieren Fehler, beschleunigen die Entwicklung und erhöhen die Ausführungsgeschwindigkeit.

Wenn Sie viel über Deep Learning gelesen haben, sind Sie wahrscheinlich auf so bekannte Frameworks wie PyTorch, TensorFlow, Theano (kürzlich für veraltet erklärt), Keras, Lasagne und DyNet gestoßen. In den letzten Jahren haben sich Frameworks sehr schnell entwickelt, und trotz der Tatsache, dass alle diese Frameworks kostenlos und Open Source verteilt werden, hat jedes von ihnen einen Geist des Wettbewerbs und der Kameradschaft.

Bisher habe ich es vermieden, Frameworks zu diskutieren, da es für Sie zunächst äußerst wichtig war, zu verstehen, was sich hinter den Kulissen abspielte, und die Algorithmen manuell zu implementieren (nur mit der NumPy-Bibliothek). Aber jetzt werden wir solche Frameworks verwenden, da die Netzwerke, die wir trainieren werden, Netzwerke mit Langzeit-Kurzzeitgedächtnis (LSTM), sehr komplex sind und der Code, der sie mit NumPy implementiert, schwer zu lesen, zu verwenden und zu debuggen ist (Gradienten in diesem Code) sind überall zu finden).

Es ist diese Komplexität, auf die Deep-Learning-Frameworks abzielen. Das Deep-Learning-Framework kann die Komplexität des Codes erheblich reduzieren (sowie die Anzahl der Fehler verringern und die Entwicklungsgeschwindigkeit erhöhen) und die Ausführungsgeschwindigkeit erhöhen, insbesondere wenn Sie einen Grafikprozessor (GPU) zum Trainieren des neuronalen Netzwerks verwenden, wodurch der Prozess um das 10-100-fache beschleunigt werden kann. Aus diesen Gründen werden die Frameworks fast überall in der Forschungsgemeinschaft verwendet, und das Verständnis der Merkmale ihrer Arbeit wird Ihnen in Ihrer Karriere als Benutzer und Deep-Learning-Forscher von Nutzen sein.

Wir werden uns jedoch nicht auf das Framework eines bestimmten Frameworks beschränken, da dies Sie daran hindert, zu lernen, wie all diese komplexen Modelle (wie LSTM) funktionieren. Stattdessen werden wir unser eigenes leichtes Framework erstellen, das den neuesten Trends bei der Entwicklung von Frameworks folgt. Wenn Sie diesem Pfad folgen, wissen Sie genau, was Frameworks tun, wenn mit ihrer Hilfe komplexe Architekturen erstellt werden. Wenn Sie versuchen, Ihr eigenes kleines Framework selbst zu erstellen, können Sie problemlos auf echte Deep-Learning-Frameworks umsteigen, da Sie die Prinzipien der Organisation einer Programmschnittstelle (API) und deren Funktionalität bereits kennen. Diese Übung war für mich sehr nützlich, und die beim Erstellen meines eigenen Frameworks gewonnenen Erkenntnisse erwiesen sich beim Debuggen von Problemmodellen als sehr hilfreich.

Wie vereinfacht das Framework Code? Wenn Sie abstrakt sprechen, müssen Sie nicht immer wieder denselben Code schreiben. Das bequemste Merkmal des Deep-Learning-Frameworks ist insbesondere die Unterstützung der automatischen Backpropagation und der automatischen Optimierung. Auf diese Weise können Sie nur direkten Verteilungscode schreiben, und das Framework kümmert sich automatisch um die Rückverteilung und Korrektur von Gewichten. Die meisten modernen Frameworks vereinfachen sogar Code, der die direkte Verteilung implementiert, indem sie übergeordnete Schnittstellen zum Definieren typischer Ebenen und Verlustfunktionen bieten.

Einführung in Tensoren

Tensoren sind eine abstrakte Form von Vektoren und Matrizen

Bis zu diesem Moment verwendeten wir Vektoren und Matrizen als Hauptstrukturen. Ich möchte Sie daran erinnern, dass eine Matrix eine Liste von Vektoren und ein Vektor eine Liste von Skalaren (einzelne Zahlen) ist. Ein Tensor ist eine abstrakte Form zur Darstellung verschachtelter Zahlenlisten. Der Vektor ist ein eindimensionaler Tensor. Die Matrix ist ein zweidimensionaler Tensor, und Strukturen mit einer großen Anzahl von Dimensionen werden als n-dimensionale Tensoren bezeichnet. Beginnen wir also mit der Erstellung eines neuen Deep-Learning-Frameworks, indem wir einen Basistyp definieren, den wir Tensor nennen:

import numpy as np class Tensor (object): def __init__(self, data): self.data = np.array(data) def __add__(self, other): return Tensor(self.data + other.data) def __repr__(self): return str(self.data.__repr__()) def __str__(self): return str(self.data.__str__()) x = Tensor([1,2,3,4,5]) print(x) [1 2 3 4 5] y = x + x print(y) [2 4 6 8 10] 

Dies ist die erste Version unserer Basisdatenstruktur. Beachten Sie, dass alle numerischen Informationen im NumPy-Array (self.data) gespeichert werden und eine einzelne Tensoroperation (Addition) unterstützt wird. Das Hinzufügen zusätzlicher Operationen ist überhaupt nicht schwierig. Fügen Sie der Tensor-Klasse einfach zusätzliche Funktionen mit der entsprechenden Funktionalität hinzu.

Einführung in die automatische Gradientenberechnung (autograd)

Zuvor haben wir eine manuelle Rückausbreitung durchgeführt. Jetzt machen wir es automatisch!

In Kapitel 4 haben wir Derivate eingeführt. Seitdem haben wir diese Ableitungen in jedem neuen neuronalen Netzwerk manuell berechnet. Ich möchte Sie daran erinnern, dass dies durch umgekehrte Bewegung durch das neuronale Netzwerk erreicht wird: Zuerst wird der Gradient am Ausgang des Netzwerks berechnet, dann wird dieses Ergebnis verwendet, um die Ableitung in der vorherigen Komponente zu berechnen, und so weiter, bis die richtigen Gradienten für alle Gewichte in der Architektur bestimmt sind. Diese Logik zur Berechnung von Gradienten kann auch der Tensorklasse hinzugefügt werden. Das Folgende zeigt, was ich vorhatte.

 import numpy as np class Tensor (object): def __init__(self, data, creators=None, creation_op=None): self.data = np.array(data) self.creation_op = creation_op self.creators = creators self.grad = None def backward(self, grad): self.grad = grad if(self.creation_op == "add"): self.creators[0].backward(grad) self.creators[1].backward(grad) def __add__(self, other): return Tensor(self.data + other.data, creators=[self,other], creation_op="add") def __repr__(self): return str(self.data.__repr__()) def __str__(self): return str(self.data.__str__()) x = Tensor([1,2,3,4,5]) y = Tensor([2,2,2,2,2]) z = x + y z.backward(Tensor(np.array([1,1,1,1,1]))) 

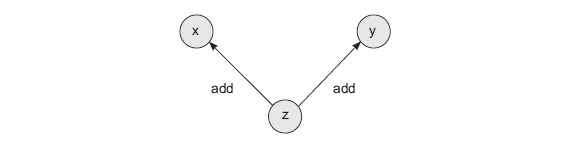
Diese Methode führt zwei Neuerungen ein. Zunächst erhält jeder Tensor zwei neue Attribute. Ersteller ist eine Liste aller Tensoren, die zum Erstellen des aktuellen Tensors verwendet werden (standardmäßig Keine). Das heißt, wenn der Tensor z durch Addieren der beiden anderen Tensoren x und y erhalten wird, enthält das Erstellerattribut des Tensors z die Tensoren x und y. kreation_op ist ein begleitendes Attribut, das die Operationen speichert, die beim Erstellen dieses Tensors verwendet werden. Das heißt, der Befehl z = x + y erzeugt einen Berechnungsgraphen mit drei Knoten (x, y und z) und zwei Kanten (z -> x und z -> y). Jede Kante wird durch die Operation von creation_op signiert, dh add. Dieses Diagramm hilft bei der Organisation der rekursiven Rückwärtsausbreitung von Verläufen.


Die erste Neuerung bei dieser Implementierung ist die automatische Erstellung eines Diagramms während jeder mathematischen Operation. Wenn wir z nehmen und eine andere Operation ausführen, wird das Diagramm in einer neuen Variablen fortgesetzt, die auf z verweist.

Die zweite Neuerung in dieser Version der Tensor-Klasse ist die Möglichkeit, mithilfe eines Diagramms Gradienten zu berechnen. Wenn Sie die z.backward () -Methode aufrufen, wird der Gradient für x und y übergeben, wobei die Funktion berücksichtigt wird, mit der der z (add) -Tensor erstellt wurde. Wie im obigen Beispiel gezeigt, übergeben wir den Gradientenvektor (np.array ([1,1,1,1,1]]) an z, und dieser wendet ihn auf seine Eltern an. Wie Sie sich wahrscheinlich aus Kapitel 4 erinnern, bedeutet Rückwärtsausbreitung durch Addition die Anwendung der Rückwärtsausbreitung. In diesem Fall müssen wir nur einen Farbverlauf zu x und y hinzufügen, also kopieren wir ihn von z nach x und y:

 print(x.grad) print(y.grad) print(z.creators) print(z.creation_op) [1 1 1 1 1] [1 1 1 1 1] [array([1, 2, 3, 4, 5]), array([2, 2, 2, 2, 2])] add 

Das bemerkenswerteste Merkmal dieser Form der automatischen Gradientenberechnung ist, dass sie rekursiv funktioniert - jeder Vektor ruft die .backward () -Methode aller seiner Eltern aus der Liste self.creators auf:


»Weitere Informationen zum Buch finden Sie auf der Website des Herausgebers
» Inhalt
» Auszug

25% Rabatt auf den Gutschein für Straßenhändler - Deep Learning
Nach Bezahlung der Papierversion des Buches wird ein elektronisches Buch per E-Mail verschickt.