
Viele Bitcoin-Geldbörsen bevorzugen bei der Auswahl der zu sendenden Münzen die Verwendung einer großen Münze, deren Kontostand größer ist als der gesendete Betrag. Nach jeder solchen Transaktion wird eine Wechselmünze gebildet. Nach einiger Zeit ist die gesamte Brieftasche mit solchen Münzen in der Größenordnung von 0,001 (derzeit ~ 10 US-Dollar) bewachsen, für die es bereits nichts mehr gibt. Als ich erneut eine Transaktion durchführen musste, kam mir der Gedanke, ob es möglich war, die Transaktion so zusammenzustellen, dass sich nichts änderte. Die Brieftasche bot hartnäckig an, eine weitere größere Münze zu "schneiden", und so beschloss ich, mit meinen Händen Münzen zu pflücken, um den erforderlichen Betrag zu sammeln. Dies stellte sich jedoch als nicht so einfach heraus: Die Summe war entweder kleiner als der gewünschte Wert oder überschritt ihn zu sehr. Aus diesem Grund habe ich beschlossen, dass es einen Algorithmus geben sollte, mit dem Sie den gewünschten Betrag aus Münzen oder etwas mehr sammeln können. Es stellte sich heraus, dass dies nicht nur möglich ist, sondern auch so gut funktioniert, dass ich diesen Artikel geschrieben habe. Aber das Wichtigste zuerst.
Rucksackproblem
Das Rucksackproblem ist allgemein bekannt: so viele wertvolle Dinge wie möglich in einen Rucksack zu packen, vorausgesetzt, die Kapazität des Rucksacks ist begrenzt. In diesem Fall haben wir den Fall des 0-1-Rucksackproblems , da jeder Artikel (Münze) nur einmal zum Packen im Rucksack verfügbar ist. Darüber hinaus stimmt das Gewicht jedes „Elements“ mit seinem Wert überein, sodass es sich um einen noch spezielleren Fall handelt, das Problem der Summe der Teilmengen . Wikipedia schlägt die Verwendung eines genetischen Algorithmus vor, aber ich habe mich entschlossen, mithilfe der dynamischen Programmierung nach einer genauen Lösung zu suchen, da dies in Bezug auf Ressourcen durchaus erreichbar ist und einfach aussieht.
Um das Problem der Auswahl von Münzen auf die Aufgabe eines Rucksacks zu reduzieren, müssen Sie eine kleine Konvertierung der Eingabedaten vornehmen. Tatsache ist, dass die Lösung des Rucksackproblems (genauer gesagt die Summe der Teilmengen) eine Teilmenge der ursprünglichen Menge ergibt, deren maximale Menge den Parameter (Rucksacktragfähigkeit) nicht überschreitet. Wir sind jedoch nicht zufrieden mit der Kombination von Münzen, da der Betrag geringer ist als der Betrag, den wir senden möchten. Wir fühlen uns jedoch mit Kombinationen wohl, die etwas überlegen sind. Wenn wir beispielsweise 0,005 Bitcoins senden müssen und eine Kombination gefunden haben, die 0,00499 ergibt, ist dies für uns nutzlos, da es weniger ist als der vom Verkäufer gewünschte Betrag. Wenn wir jedoch 0,005001 finden, ist das richtig. Zusätzliches Satoshiki kann als Provision verwendet werden (wir werden weiter unten ausführlich darauf eingehen) oder es dem Verkäufer geben, wenn er das Senden eines größeren Betrags zulässt. Daher müssen wir mit Hilfe des Rucksackproblems nicht die Münzen auswählen , die gesendet werden müssen , sondern diejenigen, die zurückgelassen werden müssen. Dann wird der maximale "Mangel" in Bezug auf das ursprüngliche Problem zu einer "Pleite".
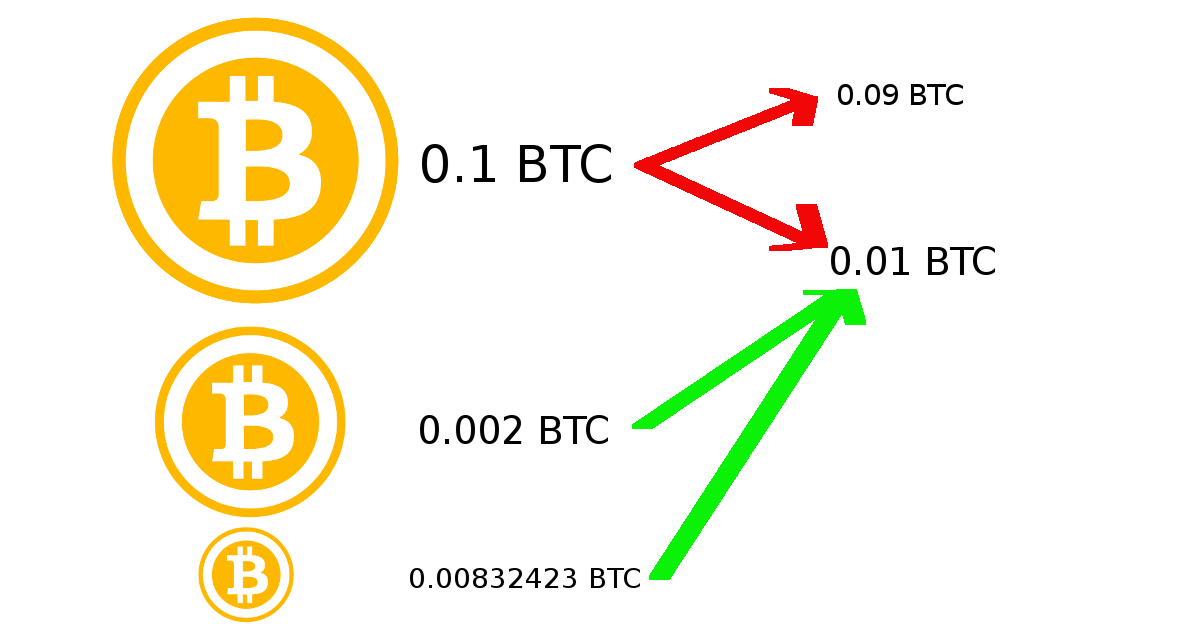
Ein Beispiel. Angenommen, wir haben solche Münzen: 0,1 BTC, 0,002 BTC, 0,00832423 BTC. Und wir müssen 0,01 BTC senden. Wir werden solche Münzen finden, deren Summe maximal ist, aber kleiner oder gleich dem Gesamtbetrag unserer Münzen abzüglich des gesendeten Betrags, dh einer solchen Zahl: 0,1 + 0,002 + 0,00832423 - 0,01 = 0,10032423. In diesem Fall stellt eine einfache Suche fest, dass es sich um eine 0,1-Münze handelt. Wir verlassen es, was bedeutet, dass wir den Rest senden: 0,002 BTC und 0,00832423 BTC, was insgesamt 0,01032423 BTC ergibt, was mehr als 0,01 BTC ist und zu uns passt. (Die Provision belief sich zwar auf 3 US-Dollar, aber sagen wir, das Netzwerk ist ausgelastet und wir möchten das Senden so schnell wie möglich gestalten.)
Provisionen
Um die Transaktionsgebühren zu berücksichtigen, habe ich jede Eingabemünze geändert und ihr Guthaben um den Betrag reduziert, der für die Aufnahme in die Transaktion als Eingabe gezahlt werden müsste. Dies kann erreicht werden, indem die Größe der Eingabe und die Provision bekannt sind (z. B. 2 Satoshi pro Byte). Außerdem habe ich den zu sendenden Betrag geändert und den Preis des Teils der Transaktion hinzugefügt, der nicht von den ausgewählten Münzen abhängt: Überschrift und Ausgang (e). Der Benutzer kann alle diese Parameter mithilfe von Flags angeben. Sie können die Anpassung für Provisionen im Allgemeinen auch deaktivieren, indem Sie eine Provision von 0 Satoshi pro Byte angeben.
Ich habe Informationen über die Größe der Ein- und Ausgänge in verschiedenen Adressversionen (klassisches, verpacktes Segwit und natives Segwit) von hier abgerufen: https://bitcoin.stackexchange.com/a/84006
Algorithmen und Implementierung
Ich habe den genetischen Algorithmus sofort fallen lassen, vielleicht vergebens. Konzentriert sich auf genaue Algorithmen. Mein erster Versuch war es, durch umfassende Suche aller Kombinationen zu realisieren, aber selbst bei 40 Münzen funktionierte es stundenlang und musste es aufgeben. Dann habe ich die auf Wikipedia vorgeschlagene dynamische Programmierung ausprobiert. Darin können Sie nicht die gesamte Matrix speichern, sondern nur die aktuellen und vorherigen Zeilen. Außerdem müssen wir den Wert nicht speichern, da er mit dem Gewicht übereinstimmt und die Spaltennummer ist. Aber wir müssen uns an die Kombination erinnern - ich habe beschlossen, sie in Form eines Bitsets zu speichern. Darüber hinaus können Sie nur eine Zeile speichern und die nächste Zeile direkt daraus erstellen. Jeder Zeilendatensatz ungleich Null bleibt an seiner Stelle und wird (unter Hinzufügung des entsprechenden Bits) eine bestimmte Anzahl von Zellen rechts in eine andere Zelle kopiert (falls er dort zuvor leer war). Wenn Sie in umgekehrter Reihenfolge die Zelle sortieren, in die der "Sprung" geht, können Sie alles richtig füllen:

Jede Zelle ungleich Null in der aktuellen Zeile wird in der nächsten Zeile selbst und eine weitere Zelle für eine bestimmte Anzahl von Zellen (gleich dem Wert der hinzugefügten Münze) rechts generiert. Wenn diese Zelle bereits einen Wert hat, „gewinnt“ die Option mit der größten Anzahl ausgewählter (dh nicht in der Transaktion enthaltener) Münzen, da wir so wenige Münzen wie möglich senden möchten, wobei andere Dinge gleich sind.
Für eine Zelle gebe ich 8 Bytes für ein Bitset aus, und die Anzahl der Zellen entspricht der möglichen Anzahl von Guthaben von 0 bis zur Anzahl der Münzen abzüglich der gesendeten Menge. Wenn sich beispielsweise nur 1 Bitcoin in der Brieftasche befindet und 0,1 gesendet wird, gibt es 100'000'000-10'000'000 = 90'000'000 Zellen mit jeweils 8 Bytes, dh 720 Megabyte - ein wenig für einen modernen Computer. Wenn die Anzahl der Münzen weniger als 32 beträgt, können 4 Bytes pro Münze verwendet werden, aber ich habe sie nicht optimiert. Wenn mehr als 64 Münzen vorhanden sind, funktioniert das Programm nicht - dies müsste auch behoben werden, indem ein Bit-Set beliebiger Länge erstellt wird. Schließlich können Sie das letzte Zeichen in den Salden verwerfen, wobei Sie ein wenig an Genauigkeit verlieren, aber 10 Mal im Speicher gewinnen. Aber soweit wird es reichen.
Ich habe das Programm unveränderlich aufgerufen und auf dem Gitlab abgelegt: gitlab.com/starius/changeless . Es ist in Go geschrieben und wird wie gewohnt mit go get . In CI gesammelte Binärdateien für Linux, Windows, Mac sind verfügbar.
Als ich das Programm mit echten Münzen startete, war ich erstaunt, wie genau sie die notwendige Kombination aufnahm. Wenn die Anzahl der Münzen groß ist, kann fast jeder Betrag, der dem Guthaben der Münzen entspricht, mit Genauigkeit bis hinunter zu Satoshi ausgewählt werden! Sie ändern den erforderlichen Betrag für 1 Satoshi und das Programm bietet genau für diesen Betrag eine völlig andere Kombination von Münzen. Unten sehen Sie ein Beispiel für die Arbeit an 50 zufälligen Münzen mit einem Guthaben von 0 bis 1 Bitcoin.
$ cat coins50.txt 0.01331611 0.03906237 0.04847086 0.08453118 0.09748168 0.10395389 0.10619825 0.12156721 0.12923149 0.13587973 0.14798976 0.16053788 0.19011834 0.21570038 0.21946913 0.31861430 0.33435508 0.33718842 0.33789473 0.35976748 0.37360122 0.44944553 0.47572926 0.49927495 0.50992142 0.53062326 0.53079433 0.53542072 0.54715225 0.55019714 0.55313907 0.56656642 0.56673333 0.65879650 0.66228482 0.68424322 0.70436496 0.75638055 0.79095597 0.82438005 0.83684407 0.85151564 0.86862948 0.90054250 0.90239402 0.91636213 0.93087757 0.93579251 0.97207439 0.98248384 $ changeless -amount 10.00000000 -coins coins50.txt Processing item 50/50. 0.09748168 + 0.33435508 + 0.47572926 + 0.53542072 + 0.66228482 + 0.70436496 + 0.75638055 + 0.82438005 + 0.9005425 + 0.90239402 + 0.91636213 + 0.93579251 + 0.97207439 + 0.98248384 = 10.00004651 Tx size: 2118 vBytes. Total fees: 0.00004651 BTC (2.2 sats/vByte). $ changeless -amount 10.00000001 -coins coins50.txt Processing item 50/50. 0.01331611 + 0.09748168 + 0.53079433 + 0.56656642 + 0.70436496 + 0.75638055 + 0.82438005 + 0.86862948 + 0.9005425 + 0.91636213 + 0.93087757 + 0.93579251 + 0.97207439 + 0.98248384 = 10.00004652 Tx size: 2118 vBytes. Total fees: 0.00004651 BTC (2.2 sats/vByte).
Das Programm hat es geschafft, Kombinationen von Münzen aufzunehmen, um genau 10 Bitcoins und genau 10.00000001 Bitcoins (10 Bitcoins und 1 Satoshi) zu senden. Um dies zu sehen, müssen Sie die Provision von der Anzahl der Münzen abziehen: 10.00004651 - 0.00004651 = 10, 10.00004652 - 0.00004651 = 10.00000001.
So erhalten Sie eine Liste der Münzguthaben
Für das Electrum-Programm habe ich diesen Weg gefunden (Konsolenbefehl):
' '.join((x["value"]) for x in listunspent())
Wenn Sie bestimmte Münzen ausschließen möchten, beispielsweise an einer bestimmten Adresse, können Sie dies folgendermaßen tun:
' '.join((x["value"]) for x in listunspent() if x["address"] != "bad address")
Für andere Geldbörsen fand ich keinen so einfachen Weg und musste ihn mit meinen Händen erneut eingeben.