Die Grenzdarstellung (B-rep) ist die primäre Methode zur Darstellung modellierter Objekte in den meisten geometrischen Kerneln, einschließlich unseres C3D Modeler-Kernels. Die Kernalgorithmen, mit denen Modelle bearbeitet werden, z. B. das Anwenden von Verrundungsoperationen, das Durchführen von Schneidoperationen und das Erhalten flacher Projektionen, erfordern die Präzision von B-Rep-Darstellungen. Die schnell wachsende Vielfalt von 3D-Daten in polygonalen Formaten macht die Aufgabe der Modelltransformation von Polygonen in Grenzdarstellung immer relevanter. Aus diesem Grund haben wir ein neues SDK entwickelt, C3D B-Shaper, das Teil unseres C3D Toolkits ist.
Die Verwendung eines Triangulationsalgorithmus (bekannt als Tessellation) für die Grenzdarstellung eines Modells ist relativ einfach. Das Erstellen polygonaler (tessellierter) Darstellungen ist nützlich für Visualisierungszwecke und für geometrische Berechnungen.
Die umgekehrte Transformation - von der polygonalen Darstellung zu B-rep - ist jedoch mit einer Reihe von Problemen verbunden, die mit der Komplexität beim Erkennen verschiedener Arten von Oberflächen, einschließlich Freiformtypen, zusammenhängen. Es gibt auch das Problem des Rauschens in polygonalen Modellen, die typischerweise als Ergebnis des 3D-Scannens auftreten.
Der allgemeine Prozess, mit dem C3D B-Shaper Modelle von polygonalen in B-rep-Formate umwandelt, besteht aus drei Schritten: Segmentierung, Rekonstruktion von Oberflächen und Konstruktion von b-rep-Modellen. Der Transformationsprozess ist iterativ: Wenn Benutzer aus irgendeinem Grund mit den Ergebnissen unzufrieden sind, können Korrekturen während der Segmentierungs- und Oberflächenrekonstruktionsphase vorgenommen werden.
Umwandlung einer polygonalen Darstellung in eine B-WiederholungBevor wir jedoch mit dem Prozess der b-rep-Transformation beginnen, verbessern wir die Qualität des polygonalen Quellnetzes, indem wir die folgenden Korrekturen anwenden: Koordinieren Sie die Richtungen der Normalen in benachbarten Polygonen; Löcher beseitigen; und ggf. Glättungsalgorithmen auf verrauschte Netzquellen anwenden.
Segmentierung des polygonalen Modells
Die erste Stufe der Transformation ist die Segmentierung des polygonalen Modells. Wir klassifizieren das Netzpolygon in Teilmengen (Segmente). Informationen über die Normalen an jedem Netzscheitelpunkt ermöglichen es, eine Segmentierung erster Ordnung durchzuführen und dann die anfängliche Netzaufteilung durchzuführen sowie Bereiche als flach oder stark gekrümmt zu klassifizieren. Die anfängliche Netzaufteilung basiert auf der Definition "scharfer" Kanten. Dies sind die Kanten zwischen zwei dreieckigen Polygonen, bei denen der Winkel zwischen ihren durchschnittlichen Normalen einen vordefinierten Wert überschreitet.
Eine Segmentierung zweiter Ordnung analysiert das Netz anhand seiner Hauptkrümmung, die zur Klassifizierung elementarer Oberflächen ausreicht. Bei der Berechnung von Krümmungen an Netzscheitelpunkten verwenden wir die Ergebnisse von Meyers Arbeiten (Mark Meyer, Mathieu Desbrun, Peter Schroder und Alan H. Barr, "Diskrete Differentialgeometrieoperatoren für dreieckige 2-Mannigfaltigkeiten", Visualization and Mathematics III, 2003). Bei der Definition eines diskreten Differentialoperators für triangulierte Bereiche wird für jeden anfänglichen Netzscheitelpunkt ein Satz benachbarter Scheitelpunkte (bezogen auf einen bestimmten Scheitelpunkt über eine Kante) berücksichtigt. Als nächstes wird ein diskreter Operator
K für den Scheitelpunkt berechnet. Basierend auf dem Operator werden die durchschnittlichen normalen, mittleren
KH- und Gaußschen
KG- Krümmungen am Netzscheitelpunkt definiert.
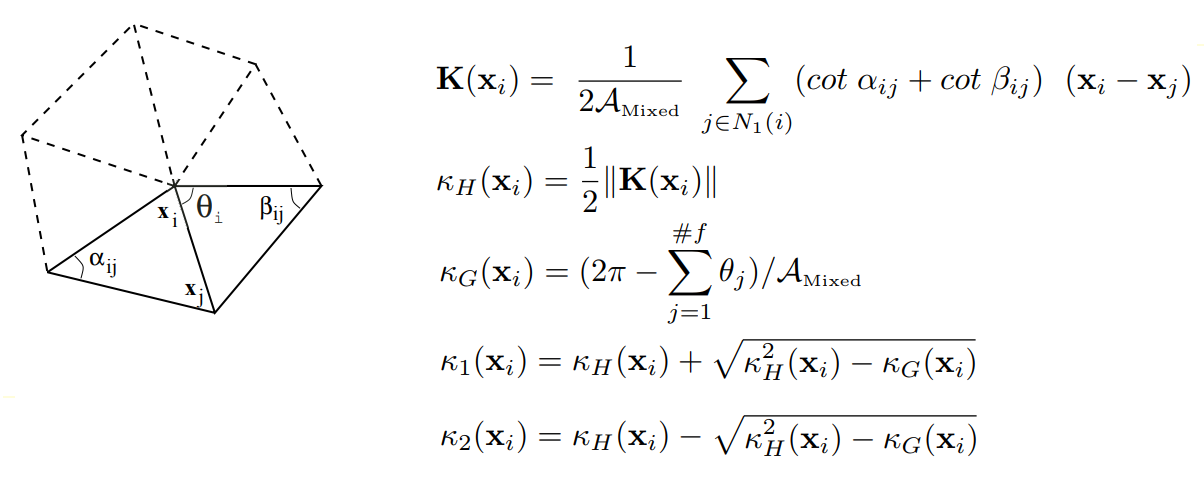Definieren diskreter Differentialoperatoren für triangulierte RegionenAuf diese Weise wird der Krümmungstensor für jeden Maschenscheitelpunkt berechnet, aus dem die Hauptkrümmungswerte
K 1 und
K 2 und die Hauptkrümmungsrichtungen extrahiert werden.
Netzscheitelpunkte werden durch die Werte ihrer Hauptkrümmungen
K 1 und
K 2 klassifiziert und dann für sie berechnet. Der Scheitelpunktklassifizierungsalgorithmus basiert auf k-Mitteln, d. H. Minimieren der gesamten quadratischen Abweichung von Clusterpunkten von den Zentren der Cluster. Die resultierende Ausgabe des Algorithmus enthält einen Netzscheitelpunkt, der einem Cluster zugeordnet ist
und ein Paar Krümmungen (Cluster-Zentrum - L. Guillaume, "Curvature Tensor Based Triangle Mesh Segmentation with Boundary Rectification", Proceedings Computer Graphics International (CGI), 2004).
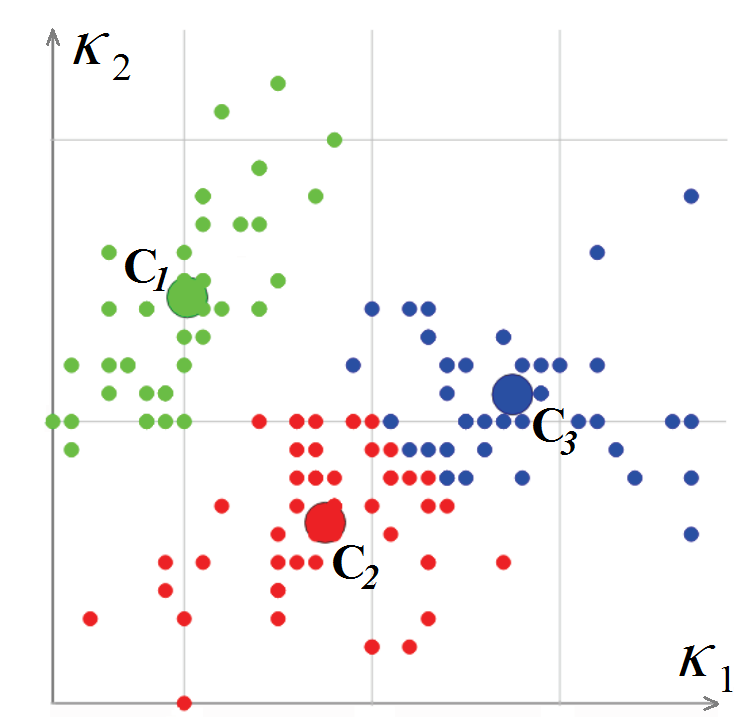Klassifizieren von polygonalen Netzscheitelpunkten im KrümmungsraumSobald wir die Eckpunkte des Polygonnetzes klassifiziert haben, fahren wir mit der Klassifizierung der Polygone fort. Um diesen Vorgang zu starten, wählen wir ein dreieckiges Polygon, dessen Krümmung als vollständig definiert betrachtet werden kann. Dies ist einer, dessen drei Eckpunkte innerhalb eines einzelnen Clusters liegen oder zwei Eckpunkte an einer scharfen Kante haben. Das Polygon wird als neues Segment bezeichnet und wird zum Ausgangspunkt für eine rekursive Prozedur, die das Segment erweitert: Für jedes dreieckige Polygon werden benachbarte Polygone berücksichtigt, solange die Kante zwischen ihnen nicht "scharf" ist. Wenn sich ein benachbarter Polygonscheitelpunkt, der einer gemeinsamen Kante gegenüberliegt, auf einer scharfen Kante befindet oder zu demselben Cluster gehört, wird das Polygon dem Segment hinzugefügt. Der Vorgang wird wiederholt, bis alle Polygone, aus denen das Netz besteht, verschwunden sind.
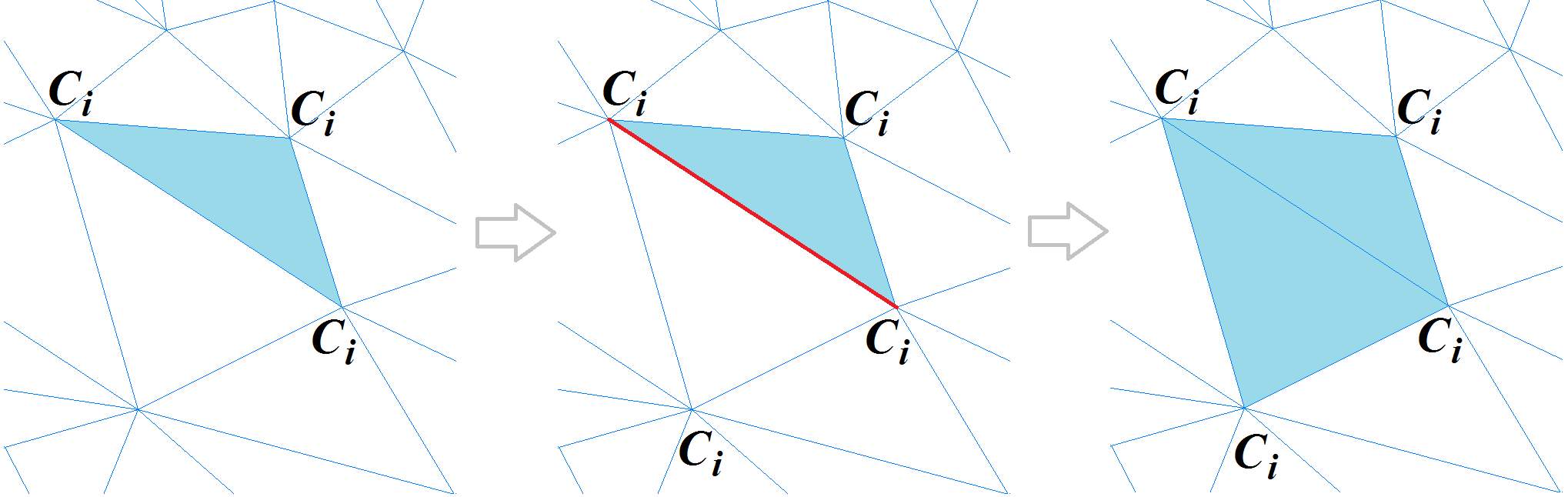Polygonale NetzsegmentierungSobald der Segmenterstellungsvorgang abgeschlossen ist, setzt ein anderer Algorithmus benachbarte Segmente zusammen, um die Über-Segmentierung des Netzes zu beseitigen.
Oberflächenerkennung
Die zweite Stufe ist die Oberflächenerkennung. Jedes Segment muss durch eine Oberfläche mit einer vom System oder vom Benutzer festgelegten Genauigkeit angenähert werden.
Zunächst wird anhand der Hauptkrümmungswerte der Segmente bestimmt, ob es überhaupt möglich ist, die Form des Segments durch eine der folgenden Elementarflächen zu beschreiben:
- Ebene: k 1 = k 2 = 0
- Kugel: k 1 = k 2 = K > 0
- Zylinder: k 1 = K > 0, k 2 = 0
- Kegel: k 1 ∈ [ a , b ], k 2 = 0
- Toroid: k 1 = K , k 2 ∈ [ a , b ]
Um elementare Oberflächen zu erstellen, passen wir einfache geometrische Objekte mit dem entsprechenden Algorithmus an Punktmengen an. Um beispielsweise einen Kreis und eine Kugel an eine Reihe von Punkten anzupassen, wird die Methode der kleinsten Quadrate verwendet. Um eine Ebene anzupassen, wird die Hauptkomponentenanalyse verwendet. Das System stellt sicher, dass jede rekonstruierte Oberfläche innerhalb einer vordefinierten Erkennungsgenauigkeit mit einem Segment verknüpft ist.
Die folgende Abbildung zeigt erkannte Oberflächen nach Farbe: Ebenen sind blau dargestellt, Zylinder rot, Kugeln grün, Zapfen gelb und Toroide violett.
Quell-Polygonnetz (links) und segmentiertes Netz (rechts) mit erkannten OberflächensegmentenWenn keine Elementarfläche das Segment beschreiben kann, versucht das System, eine Extrusionsfläche oder eine Rotationsfläche zu erkennen.
Wenn das System letztendlich keine analytische Oberfläche findet, anhand derer die Segmentform beschrieben werden kann, wird eine NURBS-Oberfläche dafür erstellt.
Erstellung von B-Rep-Modellen
Die letzte Phase der Transformation besteht darin, das B-rep-Modell basierend auf der Segmentierung und den rekonstruierten Oberflächendaten zu erstellen. Aus den segmentierten Bereichen wird ein Adjazenzdiagramm erstellt, um die Topologie des Modells darzustellen. Es bildet die Grundlage für die Erstellung des resultierenden B-rep-Modells. B-Rep-Modelle werden im Gegensatz zu den vorhergehenden Schritten in einem vollautomatischen Modus zusammengebaut:
- B-Rep-Kanten werden aus Schnittkurven benachbarter rekonstruierter Flächen erstellt
- B-Wiederholungsflächen werden durch begrenzte erkannte Oberflächen und B-Wiederholungskanten konstruiert
Es ist jedoch nicht immer möglich, eine Shell mit der richtigen Topologie zu erstellen. Nehmen Sie zum Beispiel zwei Oberflächen wie einen Zylinder und eine Ebene, die im Raum nahezu tangential zueinander sind. Aufgrund der für die rekonstruierten Oberflächen angegebenen Toleranz schneiden sie sich möglicherweise überhaupt nicht. Infolgedessen kann die erstellte Shell Fehler aufweisen. Benutzer können Fehler beseitigen, indem sie die Oberflächenparameter korrigieren.
Arten von polygonalen Modellen
Es gibt zahlreiche Quellen für polygonale Modelle, die online verfügbar sind:
- Online-Kataloge und -Datenbanken bieten 3D-Modelle in polygonalen Formaten wie STL, VRML und OBJ von 3D Warehouse, Cults 3D usw. an
- Dateien, die beim 3D-Scannen entstehen
- Ausgabe der topologischen Optimierung von Modellen mithilfe von CAE-Algorithmen
Polygonale Modelle aus diesen Quellen können in zwei Gruppen unterteilt werden: Modelle, die aus B-rep-Objekten trianguliert (vermascht) wurden, und alle anderen Modelle. Ein für die erste Gruppe spezifisches Merkmalspaar ist das Fehlen von polygonalem Netzrauschen und die Dominanz analytischer Oberflächen. Dies bedeutet, dass Modelle aus der ersten Gruppe im vollautomatischen Modus oder mit minimalem Benutzeraufwand problemlos in B-Wiederholungen umgewandelt werden können.
Polygonale Netze von Modellen der zweiten Gruppe weisen Rauschen auf, enthalten organische Oberflächen und erfordern daher eher die interaktive Teilnahme von Benutzern.
Daher bieten wir zwei Modi für den Betrieb von C3D B-Shape, vollautomatisch und interaktiv. Benutzer können während des Rekonstruktionsprozesses zwischen Erkennungsmodi wechseln und Oberflächentypen verwalten. Die Auswahl eines Modus kann vom Zweck der Durchführung der Transformation abhängen: Benutzer möchten manchmal die topologische Konnektivität der resultierenden Shell oder ihre allgemeine Korrektheit außer Acht lassen. Dies ist häufig der Fall, wenn die Anzeige in BIM-Anwendungen optimiert wird, in denen Benutzer dem Architekturmodell benutzerdefinierte Innenelemente hinzufügen.
Andererseits erfordern Reverse Engineering-Aufgaben eine möglichst genaue Kopie der Quellmodelle, damit das resultierende Modell eine korrekte Topologie aufweist. Daher ist es notwendig, die Genauigkeit der Koaxialität von Zylindern oder die Tangentialität zweier Oberflächen vorab zu definieren. In solchen Fällen ist die Beteiligung der Benutzer am Transformationsprozess von entscheidender Bedeutung.
Die automatische Transformation von C3D B-Shaper verwendet die folgenden Funktionen, die als Eingabedaten das Quellnetz und die Transformationseinstellungen verwenden:
MbResultType ConvertMeshToShell( MbMesh & mesh, MbFaceShell *& shell, const MbMeshProcessorValues & params ); MbResultType ConvertCollectionToShell( MbCollection & collection, MbFaceShell *& shell, const MbMeshProcessorValues & params );
Eine der Transformationseinstellungen ist ein Erkennungsgenauigkeitswert, der die maximale Toleranz für Abstände zwischen Segmentscheitelpunkten und erkannten Flächen festlegt. Die Genauigkeit kann absolut oder relativ sein. Bei Verwendung der relativen Genauigkeit werden die Abweichungen der Flächen von den Netzkörpern relativ zur Modellgröße gemessen.
Die MbMesh Processor-Schnittstellenklasse bietet erweiterte Optionen zum Verwalten der Segmentierung und Erkennung von Oberflächen:
class MbMeshProcessor { .. public:
Um beispielsweise die Ergebnisse der automatischen Segmentierung zu korrigieren, bietet C3D B-Shaper Tools zum Zusammenführen und Teilen von Segmenten usw. Benutzer können Oberflächen bestimmter Typen an das ausgewählte Segment anpassen und die Parameter erkannter Oberflächen ändern.
Zusammenfassung
Das Ergebnis der Transformationsalgorithmen von C3D B-Shaper wird in den folgenden Abbildungen veranschaulicht, in denen ein komplexes 3D-Modell erfolgreich von seiner polygonalen Netzdarstellung in einen Festkörper mit Grenzdarstellung transformiert wird.
Polygonales Netz (links) und B-Rep-Modell (rechts), konvertiert mit C3D B-ShaperUnser Ziel ist es, ein leistungsstarkes SDK für die Transformation von Modellen von polygonal zu B-rep zu erstellen. Daher wird die Entwicklung von C3D B-Shaper fortgesetzt. Wir arbeiten unter anderem daran, die automatischen Segmentierungsalgorithmen weiterzuentwickeln, Werkzeuge für die Segmentierungsbearbeitung zu entwickeln, die Konstruktion von Freiform-NURBS-Oberflächen zu verbessern und die Qualität von B-rep-Shell-Baugruppen zu verbessern.
Kunden, die den geometrischen C3D-Kernel verwenden, sind auch ein Faktor für die Entwicklung von C3D B-Shaper.
Entwickler können C3D B-Shaper gerne als Teil des C3D Toolkit oder als eigenständige Komponente testen.
Von Andrey Tumanin, Leiter der Softwareentwicklung bei C3D Labs