Berechnung der Nullhypothese, zum Beispiel die Analyse der Gehälter ukrainischer Programmierer

Ich habe beschlossen, es zu teilen, aber ich selbst würde nicht vergessen, wie einfache statistische Tools zur Analyse von Daten verwendet werden können. Eine anonyme Umfrage wurde als Beispiel für Gehälter, Dienstzeit und Positionen ukrainischer Programmierer für 2014 und 2019 verwendet. (1)

Analyseschritte

• Datenvorverarbeitung und vorläufige Analyse ( alle, die sich für den Code hier interessieren )
• Eine grafische Darstellung der Daten. Verteilungsdichtefunktion.
• Wir formulieren die Nullhypothese (H0) (2)
• Wählen Sie eine Metrik für die Analyse
• Wir verwenden die Bootstraping-Methode, um ein neues Datenarray zu bilden.
• Wir berechnen den p-Wert (3), um die Hypothese zu bestätigen oder zu widerlegen

Datenvorverarbeitung

Nach einigen Manipulationen (der Code ist hier ) präsentieren wir die Daten in der folgenden Form:

#      ,  . display(data_14_1.head(), data_19_1.head()) print('  : \n \ {} .  14   {}  19 '.format(len(data_14_1), len(data_19_1))) 

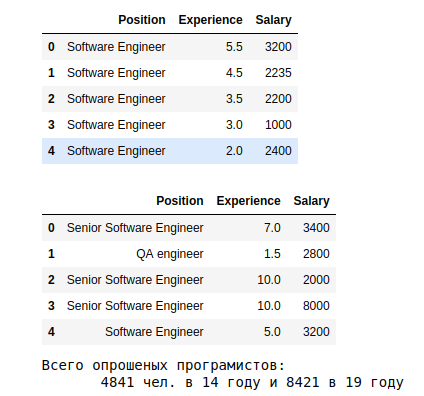
Noch ein paar Gruppierungen für ein Jahr (lassen Sie den 19.):

 # ,  19  display(pd.DataFrame(df.groupby(['Experience'])['Salary'].mean().sort_values(ascending=False)), \ pd.DataFrame(df.groupby(['Position'])['Salary'].mean().sort_values(ascending=False)), \ df.Position.value_counts()) 

Die ersten Schätzungen lauten wie folgt.

a. Die Ergebnisse zeigen, dass im Durchschnitt 19 Personen, die seit mehr als 10 Jahren arbeiten, mehr als 3,5.000 erhalten. Die Abhängigkeit der Erfahrung -> zp

c. Durchschnitt s.p. In 19 zeigen sie je nach Spezialisierung einen 10-fachen Spread - von 5k für System Architect bis 575 für Junior QA.

s Die letzte Tafel zeigt die Verteilung nach Beruf. Die meisten Daten über Software Engineer, ohne Qualifikation.

Wir machen auf die Merkmale des 19. Jahres aufmerksam: Mit dem 9. Jahr der Erfahrung stimmt etwas nicht, und es gibt keine Klassifizierung nach den Stufen Junior, Middle, Senior. Sie können die Gründe für den Ausreißer des 9. Jahres besser verstehen. Aber für diese Analyse nehmen wir es so, wie es ist.

Aber mit den Kategorien - es lohnt sich zu sortieren. im Jahr 19, der Software Engineer 2739 Personen (35% von allen) ohne Angabe des Qualifikationsniveaus. Berechnen wir den Durchschnitt und die Abweichungen für diejenigen, die angegeben haben.



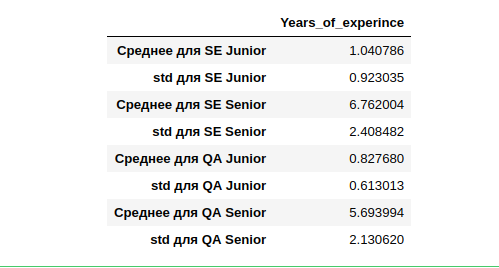
Es stellt sich heraus, dass die durchschnittliche Berufserfahrung (wer hat sie angegeben) für SE Junior ein Jahr beträgt, mit einer ziemlich großen Abweichung von einem Jahr. SE Senior hat die meiste Erfahrung mit einer ähnlich großen Abweichung von 2,4 Jahren.

Wenn wir versuchen, Middle zu berechnen und die durchschnittliche Erfahrung derjenigen zu verwenden, die es angegeben haben, um diejenige zu kategorisieren, die es nicht angegeben hat, gruppieren wir möglicherweise nicht die gesamte Stichprobe korrekt. Wir werden insbesondere bei anderen Spezialitäten (nicht SE und QA) Fehler machen, d. H. zu wenig Daten. Darüber hinaus gibt es nur wenige zum Vergleich mit dem 14. Jahr.

Was kann ich noch verwenden?

Nehmen wir nur das Gehaltsniveau als verlässlichen Indikator für das Qualifikationsniveau! (Ich denke, es wird Dissens geben).

Zunächst bauen wir auf, wie die Verteilung der Gehälter für das 19. Jahr aussieht.





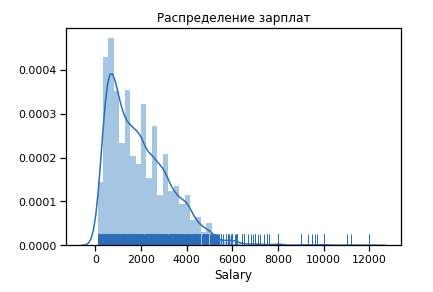
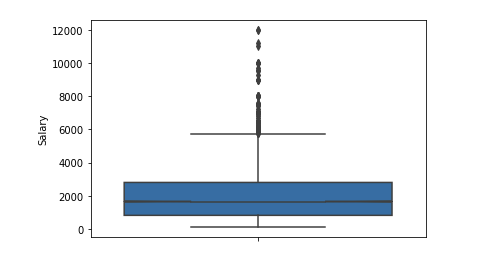
Ausreißer signifikante Zahl nach 6 $ k. Wir verlassen den Bereich der Einschränkungen [400 - 4000]. Jeder Programmierer sollte mehr als 400 bekommen :)

 df_new = data_19_1[(data_19_1['Salary'] > 400) & (data_19_1['Salary'] < 4000)] sns.distplot(df_new['Salary'], rug=True, norm_hist=True) 

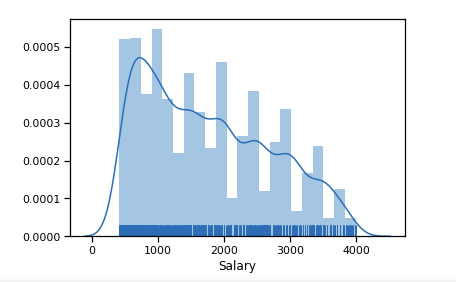
Schon etwas näher an der Normalverteilung.

Wir komponieren seit 19 Jahren, wobei die Fähigkeiten vom RFP abhängen. $ 3600 Range gibt uns eine gute Unterteilung in 3 Kategorien - $ 1200

 df_new.reset_index() df_new.loc['level'] = 0 df_new.loc[df_new.Salary <= 1200, 'level'] = 'Junior' df_new.loc[(df_new.Salary > 1200) & (df_new.Salary <= 2400), 'level'] = 'Middle' df_new.loc[df_new.Salary > 2401, 'level'] = 'Senior' 

Draw - Kategoriedichte seit 19 Jahren.

 sns.set(style="whitegrid") fig, ax = plt.subplots() fig.set_size_inches(11.7, 8.27) plt.title('      19 ') sns.barplot(x='level', y='Salary', hue='Experience', hue_order=[1,3,5,7,10], palette='Blues', \ data=df_new, ci='sd') 

Durch Hinzufügen der angegebenen Menge an Erfahrung (linke Ecke) können Sie verschiedene Nuancen sehen. Zum Beispiel, dass Junior im Durchschnitt bis zu 1k erreicht und seine Berufserfahrung 5 Jahre beträgt. Die größte Streuung in sn bei Senior (eine schwarze kurze Linie am oberen Rand jeder Spalte) und viele andere interessante Details.

Hier sind die ersten beiden Phasen beendet. Wir fahren mit dem Testen von Hypothesen mithilfe von Bootstraping fort.

Wir formulieren die Nullhypothese (H0)

In den ersten Phasen haben wir festgestellt, dass die angegebene Berufserfahrung das Qualifikationsniveau nicht sehr genau bedeutet. Dann bilden wir die Nullhypothese (die widerlegt werden muss)

Es gibt viele Möglichkeiten (zum Beispiel):

• Die Abhängigkeit des Gehalts vom Dienstalter im Jahr 14 ist dieselbe wie im 19. Jahr.
• Die Juniorgehälter haben sich seit 14 Jahren nicht geändert.

Da die angegebene Erfahrung jedoch ein schlechter Indikator ist und die Berechnung für bestimmte Kategorien verwirrend sein kann, wählen wir eine einfache und substanziellere Option: Das durchschnittliche Niveau von sn bei 14, das gleiche wie in 19, ist unsere Nullhypothese H0 (2).

Das heißt, wir gehen davon aus, dass sich die Gehälter für 5 Jahre nicht geändert haben.

NICHT die Genauigkeit der Hypothese, trotz aller Offensichtlichkeit, können wir genau überprüfen, indem wir den P-Wert für die Nullhypothese berechnen.

 #       (14  19 ),    95 % mean_salary_14 = np.mean(data_14_1['Salary']) conf_salary_14 = np.percentile(data_14_1['Salary'], [2.5, 97.5]) mean_salary_19 = np.mean(data_19_1['Salary']) conf_salary_19 = np.percentile(data_19_1['Salary'], [2.5, 97.5]) diff_mean_salary = mean_salary_19 - mean_salary_14 

Das durchschnittliche Gehalt im Jahr 14 beträgt 1797 USD, wobei das Konfidenzintervall 95% beträgt [300,0 4000,0].
Das durchschnittliche Gehalt in 19 beträgt 1949 US-Dollar, wobei das Konfidenzintervall 95% beträgt [300,0 5000,0].

Die Differenz der Durchschnittsgehälter in den Jahren 14 und 19: 152 USD

Metrik zur Analyse

Es ist logisch, die Durchschnittswerte als unsere Metrik zu wählen. Andere Optionen sind möglich, beispielsweise der Median, der häufig bei einer signifikanten Anzahl von Ausreißern durchgeführt wird. Der Durchschnitt als Schätzung ist jedoch leicht zu verstehen und gibt auch eine gute Idee.

Schreiben einer Bootstrapping-Funktion.

 #   bootstraping def bootstrap(data, func): boots = np.random.choice(data, len(data)) return func(boots) def bootstrapping(data, func=np.mean, size=1): reps = np.empty(size) for i in range(size): reps[i] = bootstrap(data, func) return reps 

Wir berechnen unsere Statistiken.

 #  14  19   -       data = np.concatenate((data_14_1['Salary'].values, data_19_1['Salary'].values)) #     2  data_mean = np.mean(data) #      14  19 ,           data_14_shifted = data_14_1['Salary'].values - np.mean(data_14_1['Salary'].values) + data_mean data_19_shifted = data_19_1['Salary'].values - np.mean(data_19_1['Salary'].values) + data_mean #  10000     ,   data_14_bootsted = bootstrapping(data_14_shifted, np.mean, size=10000) data_19_bootsted = bootstrapping(data_19_shifted, np.mean, size=10000) #       .      . mean_diff = data_19_bootsted - data_14_bootsted #  P value               . p_value = sum(mean_diff >= diff_mean_salary) / len(mean_diff) print('p-value = {}'.format(p_value)) 

p-Wert = 0,0

P-Werte bis zu 0,05 werden als unbedeutend angesehen, und in unserem Fall ist sie gleich 0. Dies bedeutet, dass die Nullhypothese widerlegt wird - die durchschnittlichen Gehaltswerte in den Jahren 14 und 19 sind unterschiedlich und dies ist kein zufälliges Ergebnis oder eine signifikante Anzahl von Ausreißern.

Wir haben im Durchschnitt 10 Tausend solcher Arrays generiert, die insgesamt nicht mehr solcher Ablösungen als die Daten selbst erhalten konnten.

Obwohl wir den ersten beiden Phasen viel Aufmerksamkeit gewidmet haben, haben wir die richtige Hypothese formuliert und die richtige Metrik ausgewählt. Bei komplexeren Aufgaben mit einer großen Anzahl von Variablen ohne solche vorbereitenden Schritte kann die Analyse zu einer falschen Interpretation führen. Überspringen Sie sie nicht.

Als Ergebnis unserer Untersuchung des Gehaltsniveaus für 14 und 19 Jahre kamen wir zu folgenden Schlussfolgerungen:

1. Basierend auf den Umfragedaten ist die angegebene Erfahrung kein vollständig geeignetes Kriterium für die Bestimmung des Gehalts- und Qualifikationsniveaus.
2. Die Einteilung in die Qualifikationsstufe basiert höchstwahrscheinlich auf der Höhe der Gehälter.
3. Die Gehälter der Programmierer stiegen von 14 auf 19 (durchschnittlich 8,5%), und dies ist kein zufälliges Ergebnis.

Vielen Dank für Ihre Aufmerksamkeit. Ich freue mich über Kommentare und Kritik.

Quellen

1. https://jobs.dou.ua/salaries/ (Umfrageergebnisse)
2. https://en.wikipedia.org/wiki/Null_hypothesis
3. https://en.wikipedia.org/wiki/P-value