Posit-Arithmetik: Besiegt einen Gleitkomma in seinem eigenen Feld. Teil 1

Teil 2

Vom Übersetzer: Das Thema des Posit-Formats war hier bereits im Mittelpunkt, jedoch ohne wesentliche technische Details. In dieser Veröffentlichung mache ich Sie auf eine Übersetzung eines Artikels von John Gustafson (Autor von Posit) und Isaac Yonemoto über das Posit-Format aufmerksam.
Da der Artikel ein großes Volumen hat, habe ich ihn in zwei Teile geteilt. Die Liste der Links befindet sich am Ende des zweiten Teils.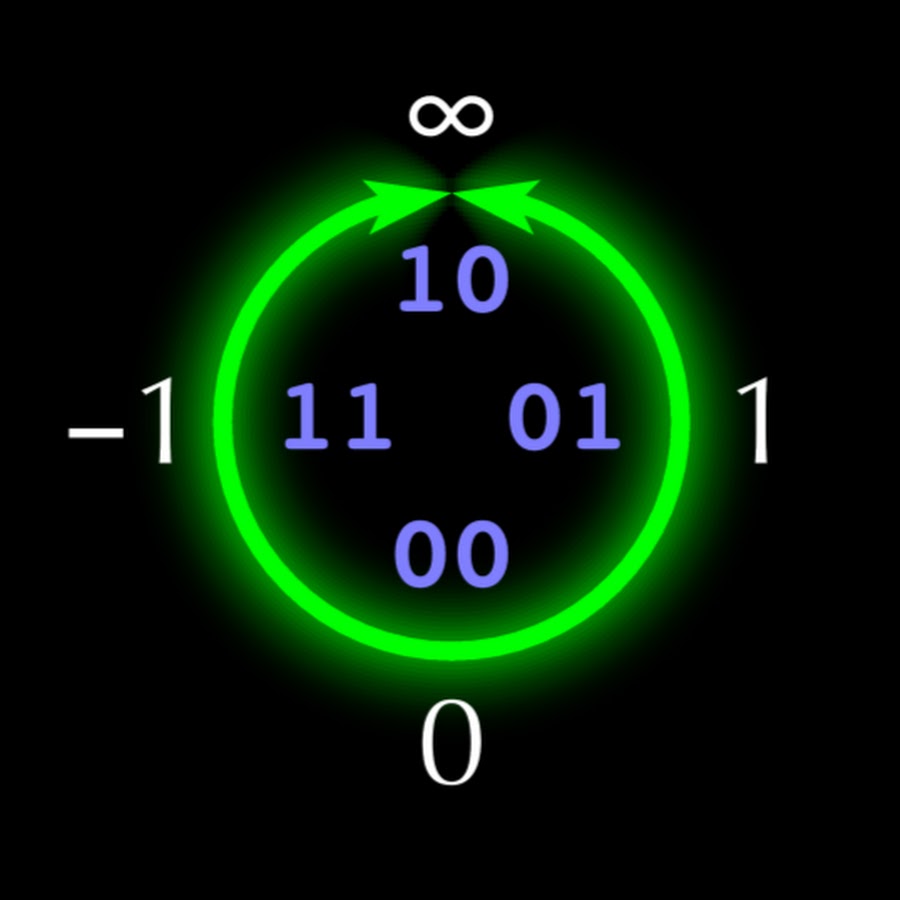



Der neue Datentyp, Posit genannt, ist als direkter Ersatz für Gleitkommazahlen des IEEE-Standards 754 konzipiert. Im Gegensatz zur früheren Form, der Unum-Arithmetik, erfordert der Posit-Standard keine Intervallarithmetik oder Operanden variabler Größe und dergleichen float, Posit-Zahlen werden gerundet, wenn das Ergebnis nicht genau dargestellt werden kann. Sie haben unbestreitbare Vorteile gegenüber dem Float-Format, einschließlich eines größeren Dynamikbereichs, einer größeren Genauigkeit, einer bitweisen Übereinstimmung der Berechnungsergebnisse auf verschiedenen Systemen, einer einfacheren Hardware und einer einfacheren Unterstützung für Ausnahmen. Die Posit-Zahlen laufen weder bis unendlich noch bis null über, und „keine Zahl“ (Not aNumber, NaN) sind Aktionen, keine Bitkombinationen. Die Posit-Verarbeitungseinheit ist weniger komplex als die IEEE-FPU. Es verbraucht weniger Strom und nimmt eine kleinere Siliziumfläche ein, sodass der Chip mit denselben Hardwareressourcen erheblich mehr Operationen mit positiven Zahlen pro Sekunde ausführen kann als FLOPS. Insbesondere GPUs und Deep-Learning-Prozessoren können mehr Operationen pro Watt Stromverbrauch ausführen, was die Qualität ihrer Arbeit verbessert.

Es wurden umfassende Tests durchgeführt, um Posit und Float hinsichtlich der Berechnungsgenauigkeit für verschiedene Positgenauigkeiten zu vergleichen. Positivzahlen mit geringer Genauigkeit sind die beste Lösung für „grobe Berechnungen“ in Fällen, in denen eine geringe Genauigkeit akzeptabel ist. Hochpräzise Posit-Nummern bieten eine höhere Genauigkeit als ein Float derselben Größe. In einigen Fällen kann ein 32-Bit-Posit einen 64-Bit-Float sicher ersetzen. Mit anderen Worten, Posit übertrifft den Float in seinem eigenen Spiel.

Theorie: Unums: Typ I und Typ II

Das arithmetische Gerüst unum (universelle Zahlen, universelle Zahlen) hat verschiedene Formen zur Darstellung von Zahlen. Die ursprüngliche Form ist "Typ I", eine Obermenge von IEEE 754; Sie verwendet Ubit am Ende des Bruchteils, um anzuzeigen, dass die reelle Zahl genau ist oder im Bereich zwischen benachbarten reellen Zahlen liegt. Trotz der Tatsache, dass Unum wie float ein Vorzeichen, einen Exponenten und einen Bruchteil hat, variieren die Längen des Exponenten und des Bruchteils automatisch von einem Bit bis zu einem vom Benutzer definierten Wert. Unum Typ I ist eine kompakte Methode zur Darstellung von Intervallarithmetik, aber variable Längen erfordern zusätzlichen Aufwand. Dieser Typ kann das Verhalten eines Schwimmers mithilfe einer speziellen Rundungsfunktion wiederholen.

Die universelle Zahlenform „Typ II“ [4] ist nicht mit dem IEEE-Float kompatibel und ist ein sauberes, mathematisch strenges Konzept, das auf projektiven reellen Zahlen x basiert. Die Schlüsselidee dabei ist, dass vorzeichenbehaftete Ganzzahlen im Add-On-Code elegant projektiven reellen Zahlen zugeordnet werden, mit der gleichen Eigenschaft, von positiven zu negativen Zahlen zu wechseln, und mit derselben Reihenfolge auf der Zahlenachse. Zitat von William Kahan [5]:
„Sie sparen Speicherplatz, weil sie nicht Zahlen, sondern Zeiger auf Werte manipulieren. Und das macht es möglich, sehr, sehr schnell zu rechnen. "
Die Struktur des 5-Bit-Unums ist in Abb. 1 dargestellt. 1. Wenn jedes Unum n Bits hat, füllt das „U-Gitter“ den oberen rechten Quadranten des Kreises mit einer geordneten Menge von $$$2 ^ {n-3} -1$ reelle Zahlen $$$x_i$ (nicht unbedingt rational). Im oberen linken Quadranten sind negativ $$$x_i$ relativ zur vertikalen Achse reflektiert. Die untere Hälfte des Kreises enthält Zahlen, die umgekehrt zu den Zahlen der oberen Hälfte sind und von der horizontalen Achse reflektiert werden, wodurch die Multiplikations- und Divisionsoperationen so symmetrisch wie Addition und Subtraktion sind. Wie bei Typ I enden Unum-Zahlen vom Typ II mit 1 (ubit), was das offene Intervall zwischen benachbarten exakten Punkten darstellt, für die Unum mit 0 endet.


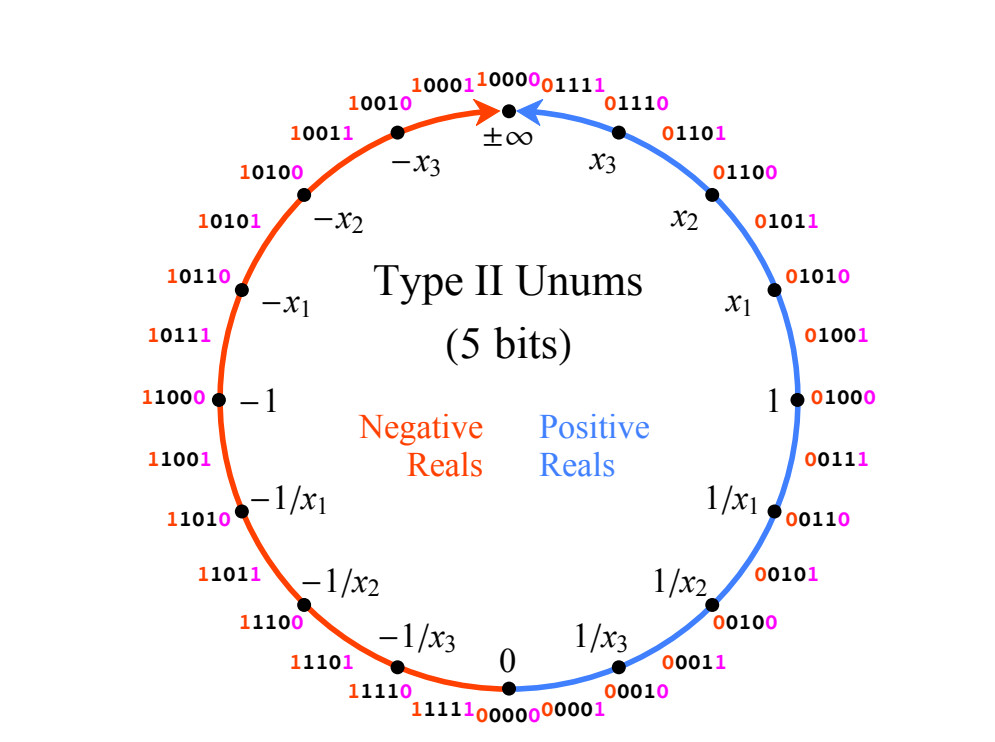Abb. 1. Die Zeile projektiver reeller Zahlen, die in einem zusätzlichen Code mit einer Länge von 4 Bit Ganzzahlen zugeordnet sind.

Unum-Zahlen vom Typ II haben viele ideale mathematische Eigenschaften, aber die meisten Operationen mit ihnen werden unter Verwendung von Nachschlagetabellen durchgeführt . Wenn n Genauigkeitsbits benötigt werden, hat die Tabelle (im schlimmsten Fall) $$$2 ^ {2n}$ Werte für die Funktion von zwei Argumenten, aber unter Berücksichtigung von Symmetrien und anderen Tricks kann die Tabelle auf eine akzeptablere Größe reduziert werden. Die Größe der Tabelle begrenzt den Maßstab dieses ultraschnellen Formats für die heutige Technologie auf 20 Bit oder weniger. Unum-Nummern vom Typ II eignen sich auch nicht gut zum Zusammenführen von Operationen. Diese Mängel dienten als Motivation, ein Format zu finden, das viele Eigenschaften von Unum-Typ-II-Nummern beibehält, jedoch „hardwarefreundlicher“ ist und von Logikschaltungen berechnet werden kann, die vorhandenen FPUs ähnlich sind.

2. Die Zahlen Posit und Valid

Es gibt zwei entgegengesetzte Ansätze für Berechnungen in reellen Zahlen:

• Nicht streng, aber billig und für eine Vielzahl praktischer Anwendungen akzeptabel
• Mathematisch streng, auch auf Kosten von Zeit und Gedächtnis

Die erste Aussage bezieht sich auf die reelle Arithmetik, bei der der Rundungsfehler klein genug ist, die zweite Aussage bezieht sich auf die Intervallarithmetik. Unum-Zahlen der Typen I und II können ebenfalls in ähnlicher Weise betrachtet werden, und dies ist einer der Gründe, warum sie "universelle Zahlen" sind. Wenn wir jedoch nach jeder Operation immer eine Funktion zum Runden verwenden, verwenden wir das letzte Bit besser nicht als signifikantes Bit des Bruchteils und nicht als Ubit. Die Nummer unum dieses Typs wird als Nummer positiv bezeichnet.

Zitat aus dem New Oxford American Dictionary, 3. Auflage:

posit (Substantiv): Eine Aussage unter der Annahme, dass sie sich als wahr herausstellen wird.

Um die Hardware-Implementierung zu vereinfachen, schwächen unum Typ II-Zahlen eine der Regeln: Exakte inverse Werte existieren nur für 0, $$$\ pm \ infty$ und Grad zwei. Dies ermöglicht es uns, das U-Gitter so zu füllen, dass die endgültigen Zahlen ähnlich wie float bleiben und die Form haben $$$m \ cdot2 ^ k$ wobei k und m ganze Zahlen sind. Es gibt keine offenen Intervalle.

Gültig ist ein Paar gleich großer Positionsnummern, die jeweils mit ubit enden. Sie sind für die Verwendung in Anwendungen vorgesehen, in denen es wichtig ist, genau zu bestimmen, in welchem ​​Intervall die Zahl liegt, beispielsweise beim Debuggen numerischer Algorithmen. Gültige Werte sind leistungsfähiger als gewöhnliche Intervallarithmetik und weniger anfällig dafür, übermäßig pessimistische Intervallgrenzen schnell zu erweitern [2, 4]. Sie sind jedoch nicht Gegenstand dieser Veröffentlichung.

Abbildung 2 zeigt den Aufbau der n-Bit-Positendarstellung mit Exponentenbits.


Abbildung 2. Verallgemeinertes Posit-Format für nachfolgende Werte ungleich Null

Das Vorzeichenbit enthält 0 für positive Zahlen, 1 für negative. Informationen zu negativen Zahlen finden Sie in Anhang 2, bevor Sie den Modus, den Exponenten und den Bruchteil dekodieren. Um die Modusbits zu verstehen, betrachten Sie die in Tabelle 1 gezeigten Binärzeichenfolgen, wobei k die Länge der führenden Sequenz und x im Bitstrom einen indifferenten Zustand bedeutet.

Tabelle 1. Lauflänge bedeutet k der Regime-Bits



Wir nennen die Länge der führenden Sequenz den Zahlenmodus. Binäre Zeichenfolgen beginnen mit einer bestimmten Anzahl von Nullen oder Einsen in einer Reihe, gefolgt vom entgegengesetzten Bit, oder das Ende der Zeichenfolge ist erreicht. Die Modusbits sind gelb hervorgehoben, das gegenüberliegende Bit ist braun hervorgehoben. Sei m die Anzahl identischer Bits in der Sequenz, wenn diese Bits Null sind, dann ist k = -m, wenn 1, dann ist k = m-1. Die meisten Prozessoren können die erste Einheit in einem Wort oder die erste Null in einem Wort in der Hardware finden, dh die Decodierungslogik ist bereits verfügbar. Modus bedeutet einen Skalierungsfaktor von $$$used ^ k$ wo $$$useed = 2 ^ {2 ^ {es}}$ . Tabelle 2 zeigt ein Beispiel für verwendete Werte.

Tabelle 2. wird als es- Funktion verwendet



Die nächsten Bits (in der Abbildung blau hervorgehoben) sind der Exponent e, der sich auf eine vorzeichenlose Ganzzahl bezieht. Es wird nicht verschoben, wie dies bei Floats der Fall ist, sondern repräsentiert die Skalierung auf $$$2 ^ e$ . Abhängig davon, wie viele Bits rechts von den Modusbits verbleiben, können bis zu es Exponentenbits vorhanden sein. Dies ist eine kompakte Methode, um die Genauigkeit zu ändern. Zahlen nahe 1 im absoluten Wert haben eine größere Genauigkeit als sehr große oder sehr kleine Zahlen, die bei Berechnungen viel seltener vorkommen.

Wenn nach den Modus- und Exponentenbits noch Bits übrig sind, stellen sie den Bruchteil f dar, genau wie der Bruchteil 1.f im Float-Format, aber das versteckte Bit ist immer 1. Im Gegensatz zu float gibt es keine denormalisierten Zahlen mit versteckter 0.

Das von uns beschriebene System ist eine natürliche Folge des Füllens des U-Gitters. Beginnen wir zur Verdeutlichung mit einer einfachen 3-Bit-Position in Abb. Abbildung 3 zeigt nur die rechte Hälfte der projektiven reellen Zahlen. Die Zahlen in Abb. 3. Befolgen Sie die Regeln von Typ II. Es gibt nur zwei spezielle Werte: 0 (alle Bits sind 0) und ± ∞ (eine Einheit, gefolgt von allen Nullen). Ihre Bitfolge folgt nicht der Positionsnotation. Für andere Positivwerte in Abbildung 3 sind die Bits wie oben beschrieben gefärbt. Es ist zu beachten, dass alle positiven Werte in 3 exakt verwendete Werte in Grad k sind, die durch Modusbits dargestellt werden.


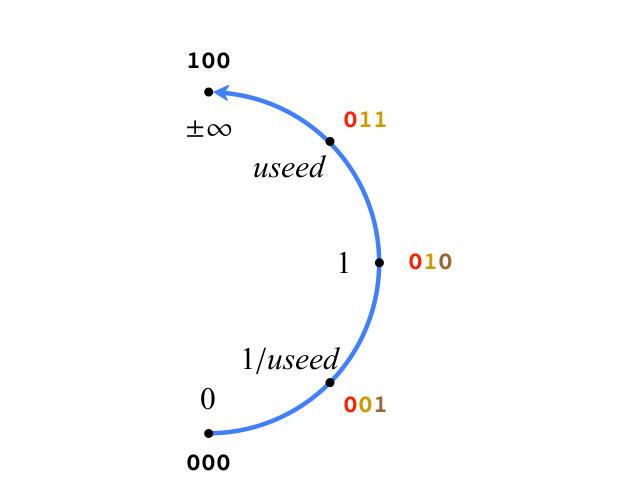Abb. 3. Positive Werte für 3-Bit-Posit

Die Genauigkeit der Posit-Zahlen erhöht sich, wenn die Bits hinzugefügt werden, und die Werte bleiben dort, wo sie sich auf dem Kreis befinden, wenn Bit 0 hinzugefügt wird. Wenn 1 hinzugefügt wird, wird ein neuer Wert zwischen den beiden Posit-Werten auf dem Kreis erstellt. Welchen numerischen Wert sollen wir ihnen zuweisen? Sei maxpos der größte positive Wert und minpos der kleinste positive Wert auf dem durch die Bitfolge definierten Kreis. In Abbildung 3 wird maxpos und minpos 1 / verwendet. Die Interpolationsregeln lauten wie folgt:

Zwischen maxpos und ± ∞ wird der neue Wert maxpos × verwendet; zwischen 0 und minpos ist der neue Wert minpos / used (mit einem neuen Modusbit)
Zwischen vorhandenen Werten $$$x = 2 ^ m$ und $$$y = 2 ^ n$ Wenn sich m und n um mehr als 1 unterscheiden, ist der neue Wert ihr geometrisches Mittel. $$$\ sqrt {x \ cdot y} = 2 ^ {(m + n) / 2}$ (mit einem neuen Exponentenbit).
In anderen Fällen befindet sich der neue Wert in der Mitte zwischen dem vorhandenen x und y, dh es handelt sich um ein arithmetisches Mittel. $$$(x + y) / 2$ (mit einem neuen Bruchbit)

Als Beispiel zeigt Abb. 4 zeigt den Aufbau von Positivzahlen von 2 bis 5 Bits mit es = 2 und somit verwendet = 16.


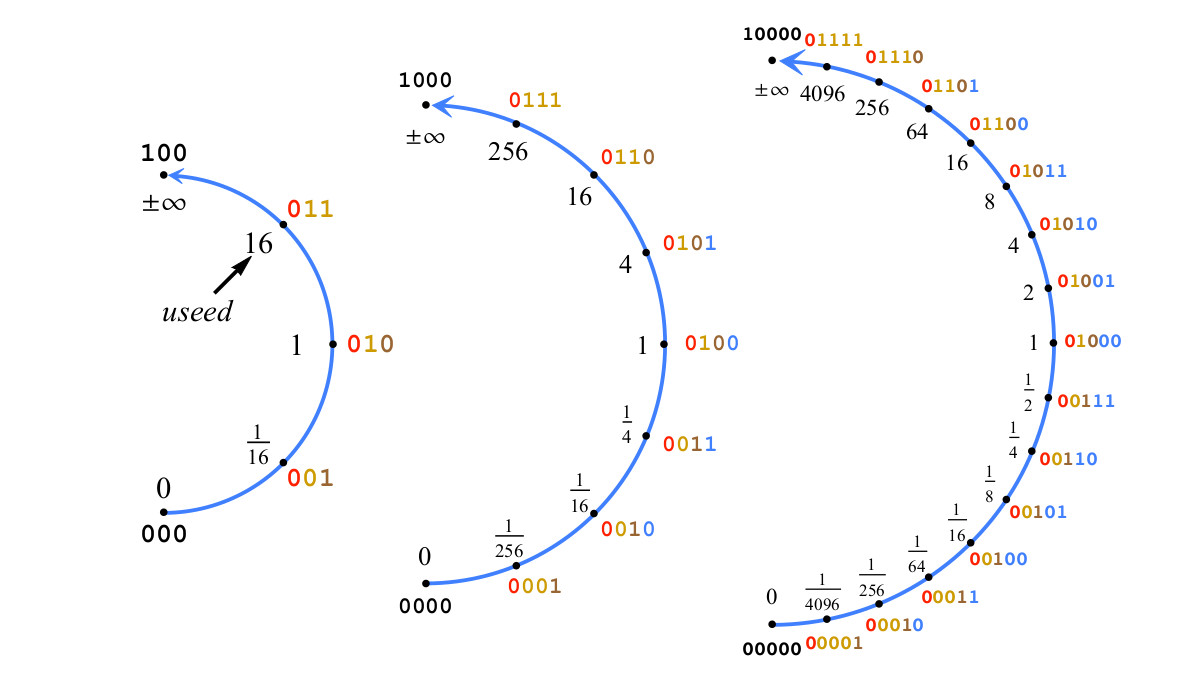Abb. 4. Erstellen einer Position mit zwei Bits eines Exponenten, $$$es = 2, used = 2 ^ {2 ^ {es}} = $ 1$

Wenn in Abb. 4 Fügen Sie ein weiteres Bit hinzu, um eine 6-Bit-Position zu erhalten. Zu den Positionsnummern, die die Wertebereiche zwischen 1/16 und 16 darstellen, wird das gebrochene Teilbit hinzugefügt, nicht das Exponentenbit. Stellen Sie sich eine Bitfolge vor, die die Zahl posit p als vorzeichenbehaftete Ganzzahl darstellt $$$-2 ^ {n-1}$ vorher $$$2 ^ {n-1} -1$ . Sei k eine ganze Zahl, die Modusbits darstellt, e eine vorzeichenlose Zahl, die Exponentenbits darstellt, falls vorhanden. Wenn das gesetzte Bit ein Bruchteil ist $$$\ {f_1f_2 ... f_ {f_s} \}$ möglicherweise leer, dann sei f ein Wert, der eine Zahl darstellt $$$1, f_1f_2 ... f_ {f_s}$ . Dann steht p für

$$

$$x = \ begin {case} 0, & p = 0, \\ \ pm \ infty, & p = -2 ^ {n-1}, \\ sign (p) \ mal verwendet ^ k \ times 2 ^ e \ times f \, & \ text {any other} p \ end {case}$$

Die Mode- und es-Bits erfüllen dieselbe Funktion wie die Exponentialbits im Standard-Float. Zusammen bestimmen sie einen Skalierungsfaktor, der einer Zweierpotenz entspricht, und jedes verwendete Inkrement bedeutet eine Verschiebung $$$2 ^ {es}$ bisschen. Die Anzahl der Maxpos ist $$$used ^ {n-2}$ und Minpos ist gleich $$$used ^ {2-n}$ . Ein Beispiel für die Decodierung der Posit-Nummer ist in Abb. 5 dargestellt (der Einfachheit halber mit einem „Nicht-Standard“ -Wert für es).


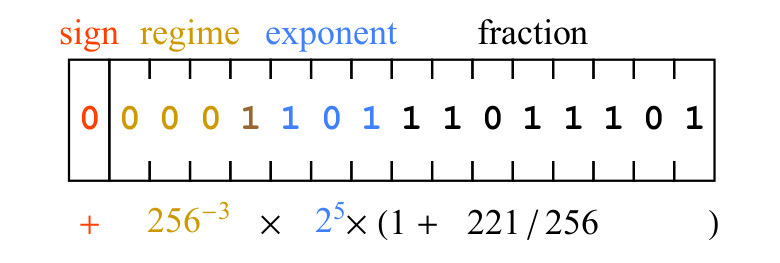Abb. 5. Ein Beispiel für die Posit-Bitfolge und ihre mathematische Bedeutung

Ein Bit mit dem Vorzeichen 0 bedeutet, dass der Wert positiv ist. Die Bits des Modus 0001 haben eine Folge von drei Nullen, was bedeutet, dass k = -3 ist, daher ist der durch die Bits des Modus eingeführte Skalierungsfaktor $$$256 ^ {- 3}$ . Die Exponentenbits 101 repräsentieren 5 als vorzeichenlose binäre Ganzzahl, und der Einfügungsskalierungsfaktor ist $$$2 ^ 5$ . Schließlich stellen die Bits des Bruchteils 11011101 die Zahl 221 dar, dh der Bruchteil ist 1 + 221/256. Der in Abbildung 5 unter dem Bitfeld geschriebene Ausdruck. führt uns zum Ergebnis $$$477/134217728 \ ca.3.55393 \ times10 ^ {- 6}$

2.2. 8-Bit-Posit- und neuronales Netzwerktraining

Trotz der Tatsache, dass der IEEE-Standard keine 8-Bit-Floats definiert, haben sich Positivzahlen von 8 Bits mit es = 0 für einige Zwecke als nützlich erwiesen. Sie sind sehr nützlich für den Aufbau neuronaler Netze [3, 8]. Derzeit werden häufig IEEE-Nummern mit halber Genauigkeit (16 Bit) für diese Zwecke verwendet, aber 8-Bit-Positivnummern können möglicherweise 2-4-mal schneller verarbeitet werden. Eine wichtige Funktion in neuronalen Netzen ist das Sigmoid, das eine Asymptote von 0 für hat $$$x \ to- \ infty$ und 1 für $$$x \ to \ infty$ . Gesamtansicht der Sigmoidfunktion $$$1 / (1 + e ^ {- x})$ und es ist teuer für Berechnungen und kann leicht mehr als hundert Zyklen des Prozessors erfordern, um die exp (x) -Funktion aus der Bibliothek aufzurufen, und wegen der Teilung. Mit Positionsnummern können Sie einfach das erste Bit der Positionszahl, die x darstellt, invertieren, die Zahl 2 Bits nach rechts verschieben, die Bits links mit Nullen füllen und die resultierende Positionsfunktion (siehe Abbildung 6). lila, nahe am Sigmoid (grün dargestellt) und hat sogar die gleiche Steigung beim Überqueren der y-Achse.


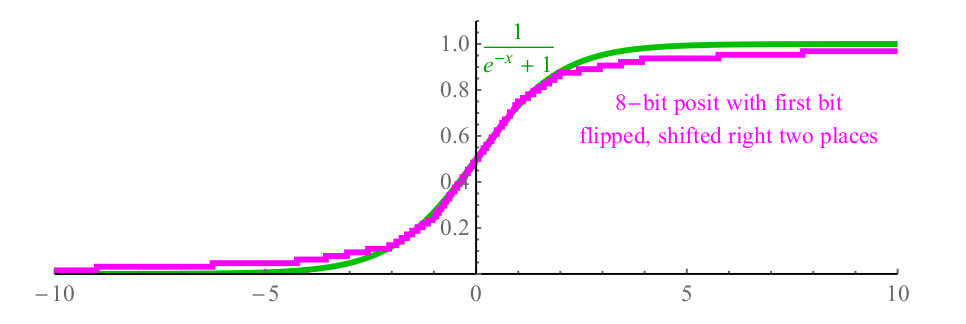Abb. 6. Schnelle Sigmoidfunktion mit Positendarstellung

2.3. Wird verwendet, um den Dynamikbereich des Schwimmers zu erreichen und zu überschreiten

Wir definieren den Dynamikbereich des Zahlensystems als die Anzahl der Dezimalstellen vom kleinsten bis zum größten positiven Endwert, von Minpos bis Maxpos. Das heißt, der Dynamikbereich ist definiert als $$$log_ {10} (maxpos) −log_ {10} (minpos) = log_ {10} (maxpos / minpos)$ . Für eine 8-Bit-Position mit es = 0 beträgt minpos 1/64 und maxpos 64, sodass der Dynamikbereich 3,6 Dezimalstellen beträgt. Die mit es = 0 definierten Posit-Nummern sind elegant und einfach, aber ihre 16- und 32-Bit-Versionen haben einen kleineren Dynamikbereich als ein IEEE-Float derselben Größe. Beispielsweise hat ein 32-Bit-IEEE-Float einen Dynamikbereich von 83 Jahrzehnten, ein 32-Bit-Posit mit es = 0 jedoch einen Dynamikbereich von nur 18 Jahrzehnten.

Nachfolgend finden Sie eine Tabelle mit es-Werten, mit denen Posit-Nummern den Dynamikbereich von float für 16- und 32-Bit-Größen überschreiten und für 64-, 128- und 256-Bit-Größen nahe kommen.

Tabelle 3. Dynamische Bereiche von Float und Posit für eine gleiche Anzahl von Bits



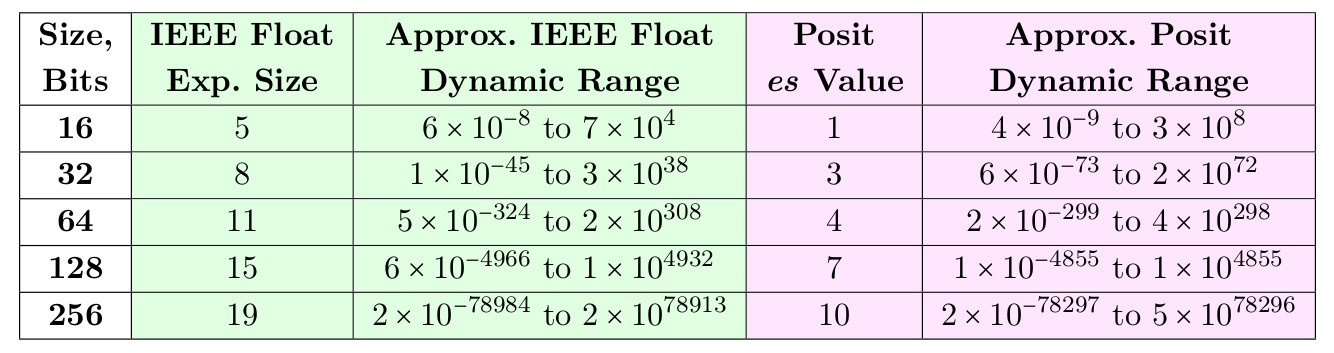
Einer der Gründe für die Wahl von es = 3 für 32-Bit-Posit ist, dass sie in diesem Fall nicht nur für einen 32-Bit-Float, sondern auch für 64-Bit als einfacher Ersatz dienen können. In ähnlicher Weise ebnet der Dynamikbereich von 17 Jahrzehnten für 16-Bit-Posits den Weg für sie in Anwendungen, die derzeit 32-Bit-Floats verwenden. Wir zeigen, dass Posit den Float sowohl im Dynamikbereich als auch in der Genauigkeit bei gleicher Bitgröße übertreffen kann.

2.4. Qualitativer Vergleich der Formate Float und Posit

Es gibt kein "NaN" im Posit-Format, stattdessen werden die Berechnungen unterbrochen, und der Interrupt-Handler muss entweder einen Fehler melden oder den Fehler irgendwie verarbeiten und die Berechnung fortsetzen, aber die Posit-Nummern erlauben nicht die Zuweisung eines bestimmten Werts, der einen logischen Fehler signalisiert , was per Definition die Zahl ist. Dies vereinfacht die Hardware erheblich. Wenn der Programmierer die Notwendigkeit sieht, NaN-Werte zu verwenden, zeigt dies, dass das Programm noch nicht abgeschlossen wurde und gültige Zahlen in der Debugging-Umgebung verwendet werden sollten, um solche Fehler zu finden und zu beseitigen. Auch Posit hat nicht $$$+ \ infty$ und $$$- \ infty$ Wie float unterstützen jedoch gültige Zahlen offene Intervalle $$$(maxpos, + \ infty)$ und $$$(- \ infty, -maxpos)$ Dies ermöglicht es, einen unbegrenzten Wert eines Zeichens darzustellen, und die Notwendigkeit einer vorzeichenbehafteten Unendlichkeit bedeutet nur, dass Sie anstelle von positiven Zahlen gültige Werte anwenden müssen.

Auch in der Posit-Ansicht gibt es keine „negative Null“, keine negative Null. Dies ist ein weiterer logischer Fehler, der im IEEE-Float-Standard vorliegt. Wenn bei Positivzahlen a = b ist, dann ist f (a) = f (b). Der IEEE 754-Standard besagt, dass die zu -0 inverse Zahl ist $$$- \ infty$ und die zu +0 inverse Zahl ist $$$+ \ infty$ , sagt aber auch, dass -0 +0 ist. Daher versteht es sich, dass $$$- \ infty = + \ infty$ ?

Float-Zahlen haben einen ausgeklügelten a = b-Vergleichsalgorithmus. Wenn eines von (a, b) NaN ist, ist das Ergebnis des Vergleichs immer negativ, selbst wenn ihre Bitdarstellung gleich ist. Wenn die Bitdarstellung unterschiedlich ist, besteht immer noch die Möglichkeit, dass a gleich b ist, da eine negative Null gleich einer positiven Null ist! In posix ist die Gleichheitsprüfung dieselbe wie für ganze Zahlen: Wenn die Bits gleich sind, sind die Zahlen gleich. Wenn ein Bit anders ist, sind sie nicht gleich. Die Posit-Nummern haben dieselbe Beziehung (a <b) wie die vorzeichenbehafteten Ganzzahlen wie bei vorzeichenbehafteten Ganzzahlen. Sie müssen sicherstellen, dass bei einem Vorzeichenwechsel kein Überlauf auftritt. Sie benötigen jedoch keine separaten Maschinenanweisungen zum Vergleichen der Posit-Werte, falls dies der Fall ist Anweisungen zum Vergleichen von vorzeichenbehafteten Ganzzahlen.

Im Posit-Format gibt es keine denormalisierten Zahlen, dh es gibt keine spezielle Bitkombination, die anzeigt, dass das versteckte Bit 0 statt 1 ist . Posit verwendet keinen Anti-Überlauf, stattdessen wird eine allmähliche Verringerung der Genauigkeit verwendet, die die Funktionalität des Anti-Überlaufs und seines symmetrischen Fallüberlaufs bietet (im Gegensatz zu Posit ist der Standard-Float asymmetrisch und verwendet diese Bitmuster, um einen großen und nutzlosen Satz von NaN-Werten darzustellen).

Das Float-Format hat gegenüber Posit einen Vorteil: Bei der Entwicklung von Hardware können sie durch eine feste Anordnung der Bits des Exponenten und des Bruchteils parallel decodiert werden.Im Posit-Format müssen Sie einer bestimmten Sequenz folgen und zuerst die Modusbits und dann die verbleibenden Bits decodieren. Es gibt eine einfache Möglichkeit, diese Einschränkung zu umgehen, ähnlich einem Trick, mit dem die Geschwindigkeit der Ausnahmebehandlung in float erhöht wird: Jedem Wert werden einige zusätzliche Bits hinzugefügt, um beim Dekodieren des Befehls Größeninformationen darin zu speichern.

3. Bitweise Kompatibilität und kombinierte Operationen

Einer der Gründe, warum IEEE Float auf verschiedenen Systemen nicht zu identischen Ergebnissen führt, liegt in elementaren Funktionen wie z $$$log(x)$ und $$$cos(x)$IEEE erfordert keine Genauigkeit bis zum letzten Bit für eine mögliche Eingabe. Die Posit-Umgebung sollte alle Ergebnisse der unterstützten arithmetischen Operationen korrekt abrunden. (Einige Programmierer von Mathematikbibliotheken sind besorgt über das „Tabellendilemma-Dilemma“, dh, dass es für einige Werte sehr kostspielig sein kann, ihre korrekte Rundung zu bestimmen. Dies kann durch die Verwendung von Interpolationstabellen anstelle von Polynomnäherungen beseitigt werden.) Falscher Wert im letzten Bit der Funktion$$$e^x$Beispielsweise kann dies letztendlich dazu führen, dass ein Computersystem uns mitteilt, dass 2 + 2 = 5 ist.

Der grundlegendere Grund dafür, dass IEEE Float auf verschiedenen Systemen keine doppelten Ergebnisse liefert, besteht darin, dass der Standard die Verwendung verschleierter Methoden ermöglicht, um einen Überlauf / Anti-Überlauf zu vermeiden und die Genauigkeit von Operationen zu verbessern, z. B. das interne Speichern eines zusätzlichen Übertragsbits für Exponential- und Bruchwerte Teile. Die Posit-Arithmetik verbietet solche versteckten Tricks.

Die neueste Version (2008) des IEEE 754-Standards [7] enthält eine kombinierte Multiplikations-Additions-Operation in den Anforderungen. Dies war eine kontroverse Änderung, die von vielen Ausschussmitgliedern nicht gebilligt wurde. Kombinierte Operationen verzögern die Rundungsoperation, bis die letzte Operation in der Berechnung, die mehr als eine Operation enthält, abgeschlossen ist, nachdem alle Operationen, einschließlich exakter ganzzahliger Operationen, abgeschlossen sind. Das Kombinieren von Operationen ist nicht dasselbe wie die erweiterbare Präzisionsarithmetik, die die Länge von ganzen Zahlen erhöhen kann, bis der Computerspeicher voll ist.

Die Posit-Umgebung erfordert das Vorhandensein der folgenden kombinierten Operationen:

Kombinierte Multiplikationsaddition$$$(a\times b)+c$
Kombinierte Addition-Multiplikation $$$(a+b)\times c$
Kombinierte Multiplikation-Multiplikation-Subtraktion $$$(a\times b)-(c\times d)$
Kombinierte Summierung $$$\sum a_i$
Kombinierte Skalarmultiplikation $$$\sum a_i b_i$

Beachten Sie, dass alle Operationen aus der obigen Liste eine Teilmenge der kombinierten Skalarmultiplikation [6] in Bezug auf die Anforderungen an die Prozessorhardware sind. Die kleinste Nicht-Null-Zahl, die durch Skalarmultiplikation erhalten werden kann, ist$$$minpos^2$ . Jedes Produkt ist eine ganzzahlige Zeit $$$minpos^2$ . Wenn wir ein skalares Produkt von Vektoren erhalten wollen $$$\{maxpos, minpos\}$ und $$$\{maxpos, minpos\}$ Als exakte Operation in einer Kratzzone benötigen wir ein Ganzes, das groß genug ist, um es zu speichern $$$maxpos^2/minpos^2$ . Erinnern Sie sich daran $$$maxpos=useed^{n-2}$ und $$$minpos=1/maxpos$ . Auf diese Weise, $$$maxpos^2/minpos^2=useed^{4n-8}$ .Unter Berücksichtigung der Übertragungsbits und der Aufrundung auf die Zweierpotenz erhalten wir die in Tabelle 4 angegebenen empfohlenen Werte.

Tabelle 4. Genaue Batteriegrößen für jede Positgröße.



In einigen Fällen ist die Batteriegröße mit der Größe des Registers vergleichbar, in anderen Fällen ist eine Kratzzone erforderlich, die dem L1- oder L2-Cache entspricht. Kombinierte Operationen können per Software oder Hardware ausgeführt werden, müssen jedoch für die Ausführung in einer positiven Umgebung verfügbar sein.