Wie Quantenverschränkung bei der Detektion von Gravitationswellen hilft

Wir haben kürzlich ein Experiment durchgeführt, um einen neuen Ansatz zur Reduzierung des Quantenrauschens in LIGO zu testen, und einen Artikel darüber geschrieben, siehe arXiv: „Demonstration der Interferometerverbesserung durch EPR-Verschränkung“ . Und hier werde ich Ihnen sagen, was Quantenrauschen in LIGO ist, wie es reduziert werden kann und was Quantenverschränkung und gequetschtes Licht damit zu tun haben.

UPD- Artikel in Nature Photonics veröffentlicht .

1. LIGO-Empfindlichkeit und Quantenrauschen

Ich habe in der letzten Veröffentlichung über das Einstein-Teleskop ausführlich darüber gesprochen, wie der Detektor funktioniert und welche Geräusche darin enthalten sind. Der Detektor weist eine Vielzahl von Störungen auf: seismische, thermische, Quanten- und andere - und alle stören die Registrierung eines Signals von Gravitationswellen.


Die Hauptbeiträge zur Empfindlichkeit von LIGO bei verschiedenen Frequenzen, normalisiert auf die Amplitude des GW (Dehnung).

Die ganze Schwierigkeit bei der Herstellung eines Gravitationswellendetektors besteht darin, diese Geräusche zu reduzieren. Die meisten dieser Geräusche sind keine grundlegenden, sondern technische Einschränkungen. Und nur Quantenrauschen entstehen aus der Natur des Messgeräts. Sie werden das Haupthindernis für eine bessere Empfindlichkeit zukünftiger Detektoren sein, daher werden wir uns näher mit ihnen befassen. Es gibt zwei Quantengeräusche: Schussrauschen und Strahlungsdruckrauschen.

Schussrauschen entsteht aufgrund der Quantennatur des Lasers: Der Laserstrahl besteht aus Photonen, die mit unterschiedlichen zufälligen Verzögerungen untereinander fliegen. Wenn diese Photonen an Fotodioden gemessen werden, führen Schwankungen des Photonenflusses zu Stromschwankungen und infolgedessen zu Rauschen im beobachteten Signal.

Das Rauschen des Strahlungsdrucks ist die zweite Seite der Quantennatur des Lichts. Wie aus dem klassischen Elektromagnetismus seit Lebedevs Experimenten bekannt ist, erfährt ein Objekt, auf das Licht scheint, Lichtdruck . Es ist leicht zu verstehen, wenn wir ein Photon als Teilchen betrachten: Jedes Teilchen trägt einen Impuls, der beim Aufprall auf den Körper übertragen wird. Das heißt, wenn der Laser auf einen beweglichen Spiegel scheint, beginnt sich der Spiegel unter dem Einfluss von Lichtdruck zu verschieben. Und da die Photonen zufällig verteilt sind, kommen manchmal mehr Photonen während eines bestimmten Zeitintervalls am Spiegel an, manchmal weniger, und diese Lichtdruckkraft ist auch zufällig. Also: Die Quantisierung von Licht führt zu einer zufälligen Kraft, die in LIGO auf die Spiegel wirkt. Diese Kraft bewirkt eine zufällige Verschiebung der Spiegel, die am Ausgang des Interferometers als Störsignal aufgezeichnet wird.


Erklärung zum Quantenrauschen. Eine zufällige Verteilung der Anzahl der Photonen erzeugt eine zufällige Kraft des Strahlungsdrucks (links). Andererseits führt eine zufällige zeitliche Verteilung der Photonen zu Amplitudenschwankungen am Fotodetektor (rechts). Beide Rauschen hängen von Wellenlänge, Lichtleistung und Schulterlänge ab. Das Rauschen des Strahlungsdrucks ist umso geringer, je größer die Masse der Spiegel ist. Gutschrift: [1].

Das Rauschen des Strahlungsdrucks ist umso stärker, je größer die auf die Spiegel einfallende Lichtleistung ist (d. H. Der Photonenfluss). Das Signal vom GW steigt auch mit zunehmender Lichtleistung im Detektor an. Das auf das Signal normierte Schussrauschen nimmt ab. Infolgedessen stellt sich heraus, dass Sie die durch Schussrauschen begrenzte Empfindlichkeit erhöhen können, indem Sie die Lichtleistung erhöhen. Sie müssen jedoch mit zunehmendem Strahlungsdruckrauschen dafür bezahlen. Umgekehrt. Auf klassische Weise gibt es keine Möglichkeit, beide Quantenrauschen gleichzeitig zu unterdrücken. Muss Quantentechnologie verwenden.


Abhängigkeit der Empfindlichkeit von der Lichtleistung: Das Schussrauschen (blau) nimmt ab und das Strahlungsdruckrauschen (grün) nimmt proportional zu.

2. Komprimiertes Licht

Es gibt einen wunderbaren Artikel über Habré über das von Qbertychon gepresste Licht. Wenn Sie nicht wissen, was komprimiertes Licht ist, empfehle ich Ihnen dringend, zuerst seinen Artikel zu lesen. Ich werde mich kurz fassen.

Wenn Sie das Licht als Welle betrachten, sind die charakteristischen Parameter nicht der Photonenfluss und die Verzögerung zwischen ihnen, sondern die Amplitude und Phase der Welle. Normalerweise sprechen sie über Phasen- und Amplitudenquadraturen von Licht.

$$$$ Anzeige $$ E = E_0 \ cos (\ omega_0 t + \ phi) = E_0 \ cos \ omega_0 t \ cos \ phi - E_0 \ sin \ omega_0 t \ sin \ phi = \\ = E_ {} \ sin \ omega_0 t + E_ {a} \ cos \ omega_0 t $$ display $$

Wenn das für uns interessante Signal in der Lichtphase enthalten ist und klein genug ist, können wir eine Annäherung vornehmen:

$$$$ display $$ E_ {f} = E_0 \ sin \ phi \ ca. E_0 \ phi; \ quad E_ {a} = E_0 \ cos \ phi \ ca. E_0 $$ Anzeige $$

Daher der Wert$$ $ inline $ E_ {f} $ inline $ Phasenquadratur genannt - enthält Informationen über die Phase.

Dementsprechend ist das Schussrauschen eine Schwankung der Lichtphase, und das Rauschen des Strahlungsdrucks wird durch Amplitudenschwankungen verursacht.

Die Unsicherheit in der Phase und die Unsicherheit in der Amplitude hängen mit der Heisenberg-Beziehung zusammen:

$$$$ Anzeige $$ \ Delta ^ 2 E_ {f} \ Delta ^ 2 E_ {a} \ leq \ frac {1} {2} $$ Anzeige $$

Bei einem herkömmlichen Laserstrahl sind diese Unsicherheiten gleich. Es ist jedoch möglich, die Unsicherheit in der Phase durch Erhöhen der Amplitudenunsicherheit zu komprimieren - die Hauptsache ist, dass ihr Produkt die Unsicherheitsrelation erfüllt. Solches Licht nennt man gequetscht:

$$$$ display $$ \ Delta ^ 2 E_ {f} ^ {sqz} = e ^ {- 2r} \ Delta ^ 2 E_ {f}, \ Delta ^ 2 E_ {a} ^ {sqz} = e ^ {2r } \ Delta ^ 2 E_ {a} \\ \ Delta ^ 2 E_ {f} ^ {sqz} \ Delta ^ 2 E_ {a} ^ {sqz} = \ Delta ^ 2 E_ {f} \ Delta ^ 2 E_ { a} \ leq \ frac {1} {2}, $$ display $$

Dabei ist r das Kompressionsverhältnis.

Im Allgemeinen bestehen auch ohne starken Strahl immer Vakuumschwankungen . Sie können auch komprimiert werden, um ein komprimiertes Vakuum zu erhalten: Im Durchschnitt ist die Anzahl der darin enthaltenen Photonen Null, aber die Schwankungen der Amplitude und Phase werden komprimiert.


Es sind die Vakuumschwankungen, die über den Signalport in den Detektor eintreten, die die Quelle des Quantenrauschens in LIGO sind. Wenn dieses Vakuum in Phase komprimiert wird, reduziert dies das Schussrauschen im Detektor.

Dieser Ansatz wurde in den letzten 8 Jahren im GEO600-Detektor verwendet, um das Schussrauschen um das Vierfache zu reduzieren. Seit diesem Jahr ist er auch in LIGO implementiert und reduziert das Schussrauschen um die Hälfte (wodurch sich die Anzahl der aufgezeichneten Ereignisse um das Achtfache erhöht).



Links: Ein Beispiel für eine verbesserte LIGO-Empfindlichkeit bei gequetschtem Licht. Rechts: Die bisher beste Komprimierung wurde in unserer Gruppe vor einigen Jahren erzielt: Vakuumschwankungen wurden um 15 dB unterdrückt.

Es ist jedoch nicht alles so einfach: Gemäß der Unsicherheitsrelation erhöhen wir, wenn wir die Phase komprimieren, die Amplitudenschwankungen. Und sie erhöhen das Rauschen des Strahlungsdrucks. Und wieder müssen Sie auswählen, welches Rauschen durch Erhöhen des anderen reduziert werden soll. Aber ist es möglich, diese Einschränkung irgendwie zu umgehen?

3. Frequenzabhängige Komprimierung

Glücklicherweise begrenzen zwei Quantenrauschen die Empfindlichkeit des Detektors bei unterschiedlichen Frequenzen: Bei geringem Rauschen ist der Strahlungsdruck viel stärker als der Schussdruck und bei hohen - umgekehrt. Daher ist es möglich, eine schwierige Kompression von Licht vorzubereiten, bei der bei niedrigen Frequenzen das Licht in der Amplitude (und damit das Strahlungsdruckrauschen reduziert wird) und bei hohen Frequenzen - in Phase (und damit das Schussrauschen) reduziert wird.


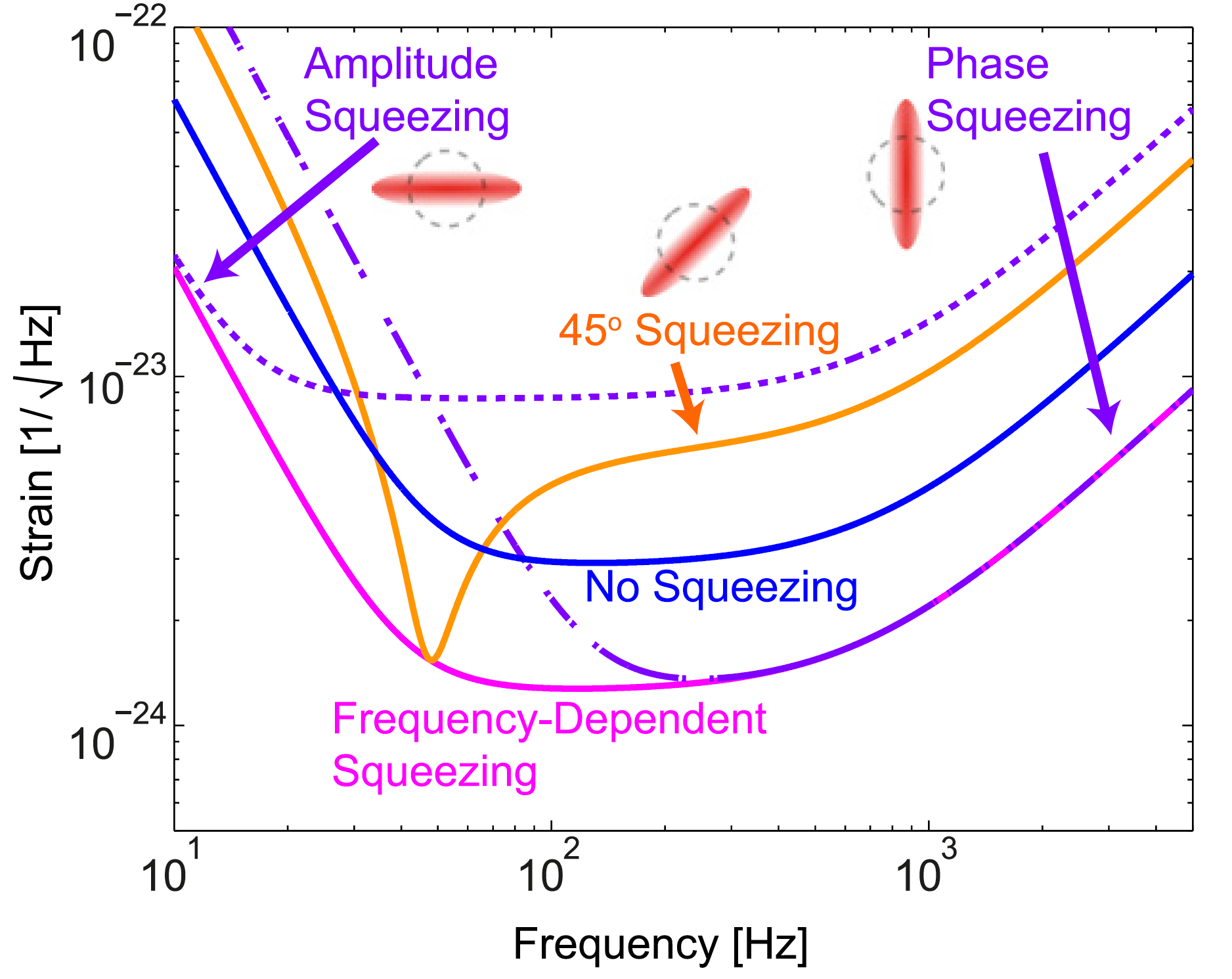Frequenzabhängige Komprimierung: Bei verschiedenen Frequenzen wird die Amplitude, Phase oder eine Kombination davon komprimiert. Infolgedessen wird die Empfindlichkeit bei allen Frequenzen verbessert. [SSY Chua et al. 2014 Class. Quantengrav. 31 183001]

Grundsätzlich liegt der Grund für die Notwendigkeit einer frequenzabhängigen Kompression darin, dass der Strahlungsdruck auf die Spiegel ebenfalls eine leichte Kompression erzeugt, jedoch in einer anderen Quadratur. Dies ist in der folgenden Abbildung zu sehen: Wenn Sie am Eingang eine herkömmliche Komprimierung verwenden, wird aufgrund des Strahlungsdrucks eine Frequenzabhängigkeit am Ausgang erfasst. Um diese Frequenzabhängigkeit "aufzuheben", müssen Sie die inverse Abhängigkeit für die Komprimierung am Eingang einstellen.


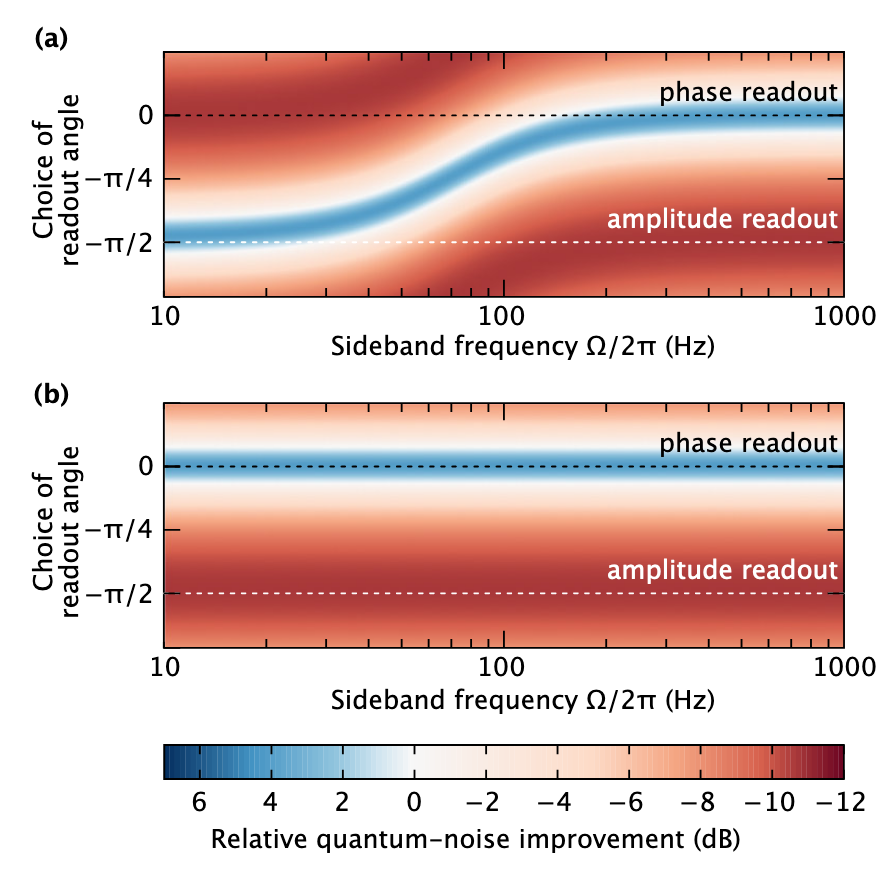Ein Beispiel aus dem Artikel: Die Abhängigkeit der Verbesserung der Empfindlichkeit des Interferometers bei Verwendung herkömmlicher Kompression als Funktion der Frequenz und verschiedener Messphasen ist oben gezeigt - das Signal befindet sich in Phasenquadratur, und es ist ersichtlich, dass die Empfindlichkeit bei hohen Frequenzen (blaue Farbe) zunimmt und bei niedrigen Frequenzen abnimmt (rot) ) Die Verwendung einer frequenzabhängigen Komprimierung kann die Empfindlichkeit bei allen Frequenzen verbessern.

Damit wir das Problem der Reduzierung des Quantenrauschens bei allen Frequenzen konzeptionell lösen, bleibt die Frage: Wie kann eine solche Frequenzabhängigkeit implementiert werden? Dazu müssen Sie herausfinden, wie Sie die komprimierte Phase in eine komprimierte Amplitude umwandeln können. In der Tat ist es sehr einfach: eine Phasenverschiebung zu erzeugen:

$$$$ display $$ E_ {f} ^ {sqz} = E_0 e ^ {- 2r} \ sin (\ phi) \ rightarrow E_0 e ^ {- 2r} \ sin (\ phi + \ pi / 2) = E_ { a} e ^ {- 2r} $$ display $$

Normalerweise reicht ein einfacher Spiegel aus, um die Phase zu verschieben, wodurch sich die Länge des Lichtwegs ändert. In diesem Fall benötigen Sie jedoch ein Gerät, das eine frequenzabhängige Phasenverschiebung erzeugt: Verschieben Sie die Phase nicht bei hohen Frequenzen, sondern bei niedrigen$$ $ inline $ \ pi / 2 $ inline $ .

Derzeit ist das führende Konzept zur Erzeugung einer frequenzabhängigen Komprimierung in allen Konstruktionen zukünftiger Detektoren die Verwendung zusätzlicher Filterresonatoren. Wenn das komprimierte Vakuum von einem solchen Resonator reflektiert wird, wenn es von der Resonanzfrequenz verstimmt wird, erhält es die notwendige Frequenzabhängigkeit. Es hat jedoch große Schwierigkeiten: Um die erforderliche Frequenzabhängigkeit zu erzeugen, müssen die Resonatoren im Vakuum mehrere hundert Meter lang sein, und dies ist sehr teuer und schwer zu steuern. Wir haben eine andere Idee.

Tatsache ist, dass es im Detektor selbst bereits viele Resonatoren geeigneter Größe, geringer Verluste und einer bekannten Regelungsmethode gibt, die jedoch nicht direkt verwendet werden können - für die frequenzabhängige Kompression ist eine Verstimmung von der Resonanz erforderlich. Jeder Resonator hat jedoch viele Resonanzfrequenzen, während der Detektor nur mit einer von ihnen arbeitet. Die Idee ist, eine andere Resonanz zu verwenden, die das vom Interferometer selbst gepresste Licht reflektiert, um die notwendige Frequenzabhängigkeit zu erhalten. Die Frage bleibt: Wie wird die Frequenzabhängigkeit verwendet, die bei einer Frequenz erzeugt wird, die sich von der Hauptarbeitsfrequenz des Lasers unterscheidet? Und dann kommt die Quantenverschränkung zur Rettung.

4. Quantenverschränkung und das EPR-Paradoxon

Die Frage nach der Art der Verstrickung verdient zweifellos einen gesonderten Artikel. Ich habe in einem früheren Artikel über das Habré etwas komplizierter gesprochen, daher werde ich hier nur kurz seine Haupteigenschaften beschreiben. Beginnen wir mit dem EPR-Paradoxon (Einstein-Podolsky-Rosen): Drei Herren bemerkten, dass die Quantenmechanik einen Haken hat. Einerseits gibt es das Unsicherheitsprinzip, das besagt, dass es unmöglich ist, die Koordinate und den Impuls eines Teilchens gleichzeitig (und in unserem Fall die Amplitude und Phase des Lichts) genau zu messen. Auf der anderen Seite kann man ein so einfaches Experiment machen: Nehmen Sie den Fall des Partikelzerfalls, bei dem zwei identische Partikel geboren werden. Nach dem Gesetz der Impulserhaltung streuen sie mit der gleichen Geschwindigkeit in entgegengesetzte Richtungen. Wenn wir den Impuls eines Teilchens messen, kennen wir genau den Impuls des zweiten Teilchens. Wenn wir die Koordinate des zweiten Teilchens messen, kennen wir gleichzeitig genau sowohl die Koordinate (wir haben sie gemessen) als auch den Impuls (wir haben sie aus der Messung des ersten Teilchens vorhergesagt), was aufgrund der Unsicherheitsrelation anscheinend unmöglich ist. Das sichtbare Paradoxon wird durch die Einführung des Konzepts der Verschränkung von Partikeln gelöst: Zwei Partikel sind nicht unabhängig voneinander, sie werden durch eine Wellenfunktion beschrieben. Diese Wellenfunktion ist nicht lokal: Bis zum Zeitpunkt der Messung ist es unmöglich zu sagen, welches der Partikel in welche Richtung geflogen ist. In gewisser Weise flogen beide gleichzeitig in beide Richtungen, und erst zum Zeitpunkt der Messung gab es eine zufällige Auswahl, welches Teilchen gemessen wurde. Ihre Koordinaten und ihr Impuls sind so miteinander verbunden, dass die Unsicherheitsrelation nicht für ihren relativen Wert gilt. Wenn eines der Partikel beispielsweise durch eine Kraft beaufschlagt wird, "fühlt" das zweite Partikel diese Kraft ebenfalls - seine gemessenen Parameter ändern sich entsprechend.

Für uns das Wichtigste: Wenn wir zwei Partikel haben, können wir die Eigenschaften des zweiten Partikels genau vorhersagen, indem wir das erste messen. Wir können den Weg eines Teilchens beeinflussen, und es wirkt auf zwei gleichzeitig. Nachdem wir die richtige Messung durchgeführt haben, können wir das Ergebnis dieses Effekts sehen.

Wie wir es verwenden (es wurde zum ersten Mal in einem Artikel in Nature Physics [2] vorgeschlagen). Die Rolle der Partikel im EPR spielen zwei Strahlen komprimierten Vakuums bei zwei Frequenzen: der Grundfrequenz des Interferometers und der Frequenz der nächsten Resonanz des Resonators. Wir verwirren sie, einer von ihnen (Hochfrequenz) wird vom abgestimmten Resonator reflektiert und gemessen. Er bekommt eine Frequenzabhängigkeit. Da die Strahlen verwickelt sind, wird diese Frequenzabhängigkeit auch mit der Grundfrequenz auf den Strahl übertragen. Nach der Messung können wir die Signale im Hauptstrahl idealerweise mit perfekter Genauigkeit vorhersagen. Dazu messen wir getrennt an zwei getrennten Detektoren und verarbeiten die Daten optimal.


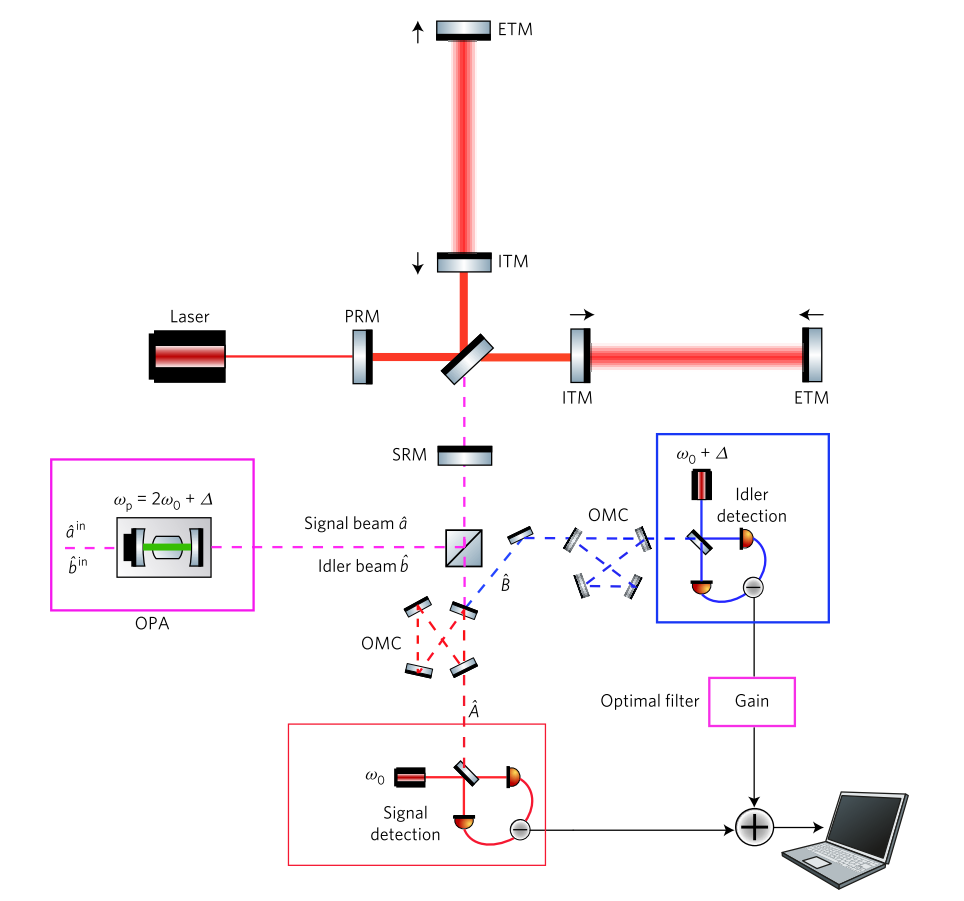Ein vollständiges frequenzabhängiges Komprimierungsschema basierend auf der Verschränkung aus [2]. OPA (Optical Parametric Amplifier) ​​erzeugt zwei verschränkte Strahlen komprimierten Vakuums mit unterschiedlichen Frequenzen, die beide an den Detektor gesendet werden. Ein Strahl mit einer Trägerfrequenz schwingt im Interferometer mit. Ein Strahl mit einer hohen Frequenz wird von einer der höheren Resonanzen verstimmt. Am Ausgang werden die Strahlen getrennt und auf zwei verschiedenen Homodyn-Detektoren detektiert, wonach sie optimal verarbeitet werden.

5. Experimentieren

Unser Experiment beinhaltet kein vollständiges Interferometer mit beweglichen Spiegeln. Stattdessen untersuchen wir die Möglichkeit, eine frequenzabhängige Komprimierung unter Verwendung von verschränktem Licht zu erzielen, das von einem Resonator reflektiert wird.


Vereinfachter Versuchsaufbau. Anstelle eines vollständigen Interferometers haben wir einen 2,5 m langen optischen Resonator. Anstelle von zwei verschiedenen Homodyn-Detektoren verwenden wir einen Detektor, aber zwei Referenzstrahlen mit unterschiedlichen Frequenzen.

Wie ich oben geschrieben habe, erzeugt der Strahlungsdruck in einem Interferometer eine Frequenzabhängigkeit des gequetschten Lichts, was die Empfindlichkeit des Detektors beeinträchtigt. Um diese Frequenzabhängigkeit aufzuheben, müssen wir eine inverse Frequenzabhängigkeit des gequetschten Lichts erzeugen. In unserem Experiment beeinträchtigt die Empfindlichkeit nicht den Strahlungsdruck (wir haben keine beweglichen Spiegel), sondern die Verstimmung des Detektors von der Resonanz (siehe Abbildung unten (a)). Bei Messung in einer Signalquadratur (Phasenanzeige) beeinträchtigt dies die Empfindlichkeit bei niedrigen Frequenzen (rot).

Um die Empfindlichkeit wiederherzustellen, bauen wir einen zusätzlichen Strahl (Leerlauf) aus Resonanz in die entgegengesetzte Richtung wieder auf. Nach der Messung können wir die Empfindlichkeit vollständig wiederherstellen. In Bezug auf EPR können wir das Ergebnis der Messung der Phasenquadratur mit Hilfe von quantenverschränktem Licht genauer vorhersagen.


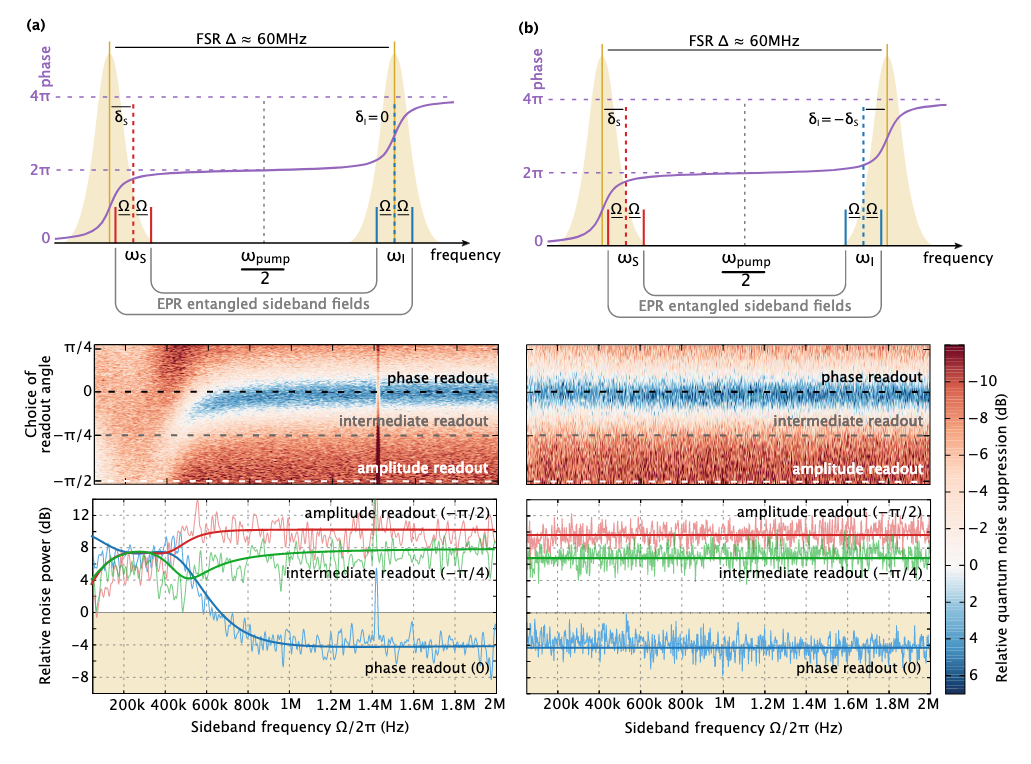Zwei Experimente zur Beobachtung der frequenzabhängigen Kompression. Im ersten (a) haben wir den Signalstrahl von der Resonanz des Detektors abgestimmt, wodurch die Empfindlichkeit in der Phasenquadratur beeinträchtigt wurde (und eine Frequenzabhängigkeit des gequetschten Lichts erzeugt wurde). Im zweiten Fall haben wir eine zusätzliche Frequenzabhängigkeit des zweiten Strahls (Leerlauf) erzeugt, und aufgrund der Quantenverschränkung zwischen den beiden Strahlen konnten Signal und ilder die beschädigte Empfindlichkeit wiederherstellen, indem sie die im ersten Experiment eingeführte Frequenzabhängigkeit aufhoben.

Im obigen Bild ist die Frequenzabhängigkeit in (a) ziemlich verschwommen. Dies liegt an Einschränkungen bei der Nachbearbeitung: Idealerweise werden zwei separate Homodyn-Detektoren benötigt, aus denen die Signale optimal gefiltert werden können. In einem anderen Modus können wir jedoch eine schöne Frequenzabhängigkeit des gequetschten Lichts erhalten, wenn wir beide Strahlen aus der Resonanz in eine Richtung wieder aufbauen. Ein solches Schema ist für den Detektor nicht relevant, gibt jedoch eine Vorstellung von den Installationsoptionen. Nun, nur schöne experimentelle Daten :)

6. Fazit

Zusammenfassend. Quantenschwankungen des Lichts sind die Haupt- und grundlegendste Rauschquelle in allen modernen und zukünftigen Detektoren. Um sie zu unterdrücken, kann man Quantenkorrelationen verwenden - gequetschtes Licht. Um jedoch das Rauschen im gesamten Frequenzbereich des Detektors zu reduzieren, müssen die Amplitudenschwankungen bei niedrigen Frequenzen und die Phasenschwankungen bei hohen Frequenzen komprimiert werden. Es wird vorgeschlagen, eine solche frequenzabhängige Kompression unter Verwendung spezieller Filterresonatoren durchzuführen. Traditionell sind solche Resonatoren sehr teuer und schwer zu implementieren. Unsere Alternative besteht darin, den Detektor selbst als Filterresonator unter Verwendung von quantenverschränktem Licht zu verwenden. Wir haben ein Experiment durchgeführt und gezeigt, dass die Quantenverschränkung es tatsächlich ermöglicht, diese Idee zu verwirklichen.

Dieser Ansatz ist leider kein Allheilmittel: Sie müssen für die Bequemlichkeit bezahlen. Damit das Konzept vollständig funktioniert, müssen zwei Homodyn-Detektoren verwendet werden, was experimentell recht schwierig ist. Darüber hinaus erhöht der zweite Detektor die Empfindlichkeit um Rauschen - wenn auch viel weniger, als Sie durch Komprimierung erzielen können.

In dieser Arbeit haben wir mit Feinheiten und zusammengedrücktem Licht herumgespielt und gezeigt, wie wir sie verwenden können, um die Empfindlichkeit zukünftiger Detektoren zu verbessern. Dies ist natürlich nur der erste Schritt auf einem langen Weg, um diesen Ansatz in einem echten Detektor zu implementieren: Sie müssen überprüfen, wie alles mit einem echten Interferometer, mit beweglichen Spiegeln, zwei Homodyn usw. funktioniert. Im Allgemeinen ist die Arbeit noch voll.

Für Detailsinteressierte siehe unseren Artikel und den Artikel, in dem die Idee erstmals vorgestellt wurde [2].

[1] S. Hild Beyond GW-Detektoren der 2. Generation
[2] Y. Ma et al., Vorschlag zur Detektion von Gravitationswellen jenseits der Standardquantengrenze durch EPR-Verschränkung, Nature Physics, Band 13, Seiten 776–780 (2017)

7. Verschiedenes

Und jetzt ein paar Neuigkeiten zu LIGO:

1. Derzeit hat LIGO in den letzten sechs Arbeitsmonaten 26 Ereignisse im O3-Arbeitszyklus registriert. Ereignisse können unter https://gracedb.ligo.org/superevents/public/O3/ überwacht werden, und es gibt eine ganze Anwendung für ein iPhone.
2. Das interessanteste war vielleicht das jüngste Ereignis mit dem möglichen Nachweis der Fusion eines Schwarzen Lochs und eines Neutronensterns. Sie können beispielsweise N + 1 oder Scientific American lesen. Im Allgemeinen ist alles sehr interessant.
3. 100 . , (c 55 130 ). , , .
4. LIGO , , , . . LIGO . , , . , , , , .

: , , : @hbar_universe .