Lineare Regression und Methoden zu ihrer Wiederherstellung

Quelle: xkcd

Die lineare Regression ist einer der grundlegenden Algorithmen für viele Bereiche der Datenanalyse. Der Grund dafür liegt auf der Hand. Dies ist ein sehr einfacher und verständlicher Algorithmus, der seit vielen zehn, wenn nicht Hunderten von Jahren zu seiner weit verbreiteten Verwendung beigetragen hat. Die Idee ist, dass wir eine lineare Abhängigkeit einer Variablen von einer Reihe anderer Variablen annehmen und dann versuchen, diese Abhängigkeit wiederherzustellen.

In diesem Artikel geht es jedoch nicht um die Anwendung der linearen Regression zur Lösung praktischer Probleme. Hier werden wir interessante Funktionen der Implementierung verteilter Algorithmen für deren Wiederherstellung diskutieren, die beim Schreiben eines maschinellen Lernmoduls in Apache Ignite aufgetreten sind. Ein wenig grundlegende Mathematik, die Grundlagen des maschinellen Lernens und des verteilten Rechnens helfen Ihnen dabei, herauszufinden, wie Sie die lineare Regression wiederherstellen können, selbst wenn die Daten auf Tausende von Knoten verteilt sind.

Worüber sprichst du?

Wir stehen vor der Aufgabe, die lineare Abhängigkeit wiederherzustellen. Als Eingabe werden viele Vektoren vermeintlich unabhängiger Variablen angegeben, von denen jeder einem bestimmten Wert der abhängigen Variablen zugeordnet ist. Diese Daten können in Form von zwei Matrizen dargestellt werden:

$$

$$\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$$

Da nun die Abhängigkeit angenommen wird und außerdem linear ist, schreiben wir unsere Annahme in Form eines Matrizenprodukts auf (um die Notation hier und unten zu vereinfachen, wird angenommen, dass der freie Term der Gleichung dahinter verborgen ist $$$x_n$und die letzte Spalte der Matrix $$$A$enthält Einheiten):

$$

$$\ begin {pmatrix} a_ {11} & a_ {12} & a_ {13} & ... & a_ {1n} \\ a_ {21} & a_ {22} & a_ {23} & ... & a_ {2n} \\ ... \\ a_ {m1} & a_ {m2} & a_ {m3} & ... & a_ {mn} \\ \ end {pmatrix} \ times \ begin {pmatrix} x_ { 1} \\ x_ {2} \\ ... \\ x_ {n} \\ \ end {pmatrix} = \ begin {pmatrix} b_ {1} \\ b_ {2} \\ ... \\ b_ {m} \\ \ end {pmatrix}$$

Sehr ähnlich einem linearen Gleichungssystem, oder? Es scheint, aber höchstwahrscheinlich wird es keine Lösungen für ein solches Gleichungssystem geben. Der Grund dafür ist das Rauschen, das in fast allen realen Daten vorhanden ist. Der Grund kann auch das Fehlen einer linearen Beziehung als solche sein, die Sie bekämpfen können, indem Sie zusätzliche Variablen einführen, die nichtlinear von der Quelle abhängen. Betrachten Sie das folgende Beispiel:

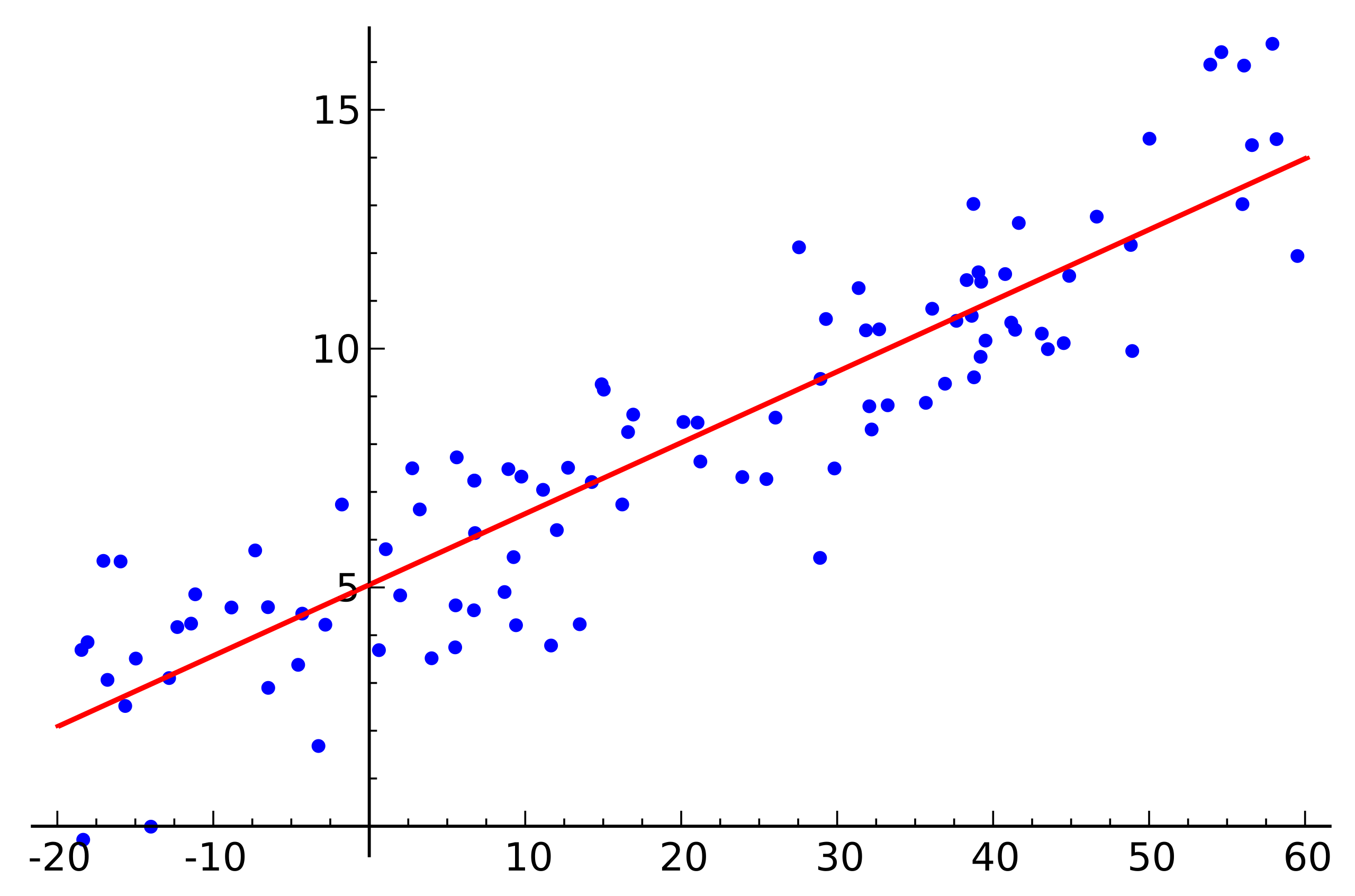Quelle: Wikipedia

Dies ist ein einfaches lineares Regressionsbeispiel, das die Abhängigkeit einer Variablen (entlang der Achse) zeigt $$$y$) von einer anderen Variablen (entlang der Achse $$$x$) Damit das diesem Beispiel entsprechende lineare Gleichungssystem eine Lösung hat, müssen alle Punkte genau auf einer geraden Linie liegen. Aber das ist nicht so. Sie liegen jedoch nicht gerade aufgrund von Rauschen auf einer geraden Linie (oder weil die Annahme des Vorhandenseins einer linearen Abhängigkeit falsch war). Um eine lineare Abhängigkeit von realen Daten wiederherzustellen, ist es normalerweise notwendig, eine weitere Annahme einzuführen: Die Eingabedaten enthalten Rauschen und dieses Rauschen hat eine Normalverteilung . Man kann Annahmen über andere Arten der Geräuschverteilung treffen, aber in den allermeisten Fällen wird später auf die Normalverteilung eingegangen.

Maximum-Likelihood-Methode

Wir haben also angenommen, dass zufälliges normalverteiltes Rauschen vorhanden ist. Wie kann man in einer solchen Situation sein? Für diesen Fall gibt es in der Mathematik die Maximum-Likelihood-Methode, die weit verbreitet ist. Kurz gesagt, sein Wesen liegt in der Wahl der Wahrscheinlichkeitsfunktion und ihrer anschließenden Maximierung.

Wir kehren zur Wiederherstellung der linearen Abhängigkeit von Daten mit normalem Rauschen zurück. Beachten Sie, dass die angenommene lineare Beziehung eine mathematische Erwartung ist $$$\ mu$verfügbare Normalverteilung. Gleichzeitig ist die Wahrscheinlichkeit, dass $$$\ mu$nimmt den einen oder anderen Wert an, sofern Observable vorhanden sind $$$x$sieht wie folgt aus:

$$

$$P (\ mu \ mid X, \ sigma ^ 2) = \ prod_ {x \ in X} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(x- \ mu) ^ 2} {2 \ sigma ^ 2}}}$$

Wir ersetzen jetzt stattdessen $$$\ mu$und $$$X$Variablen, die wir brauchen:

$$

$$P (x \ mid A, B, \ sigma ^ 2) = \ prod_ {i \ in [1, m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}}}, a_i \ in A, b_i \ in B$$

Es bleibt nur der Vektor zu finden $$$x$bei der diese Wahrscheinlichkeit maximal ist. Um eine solche Funktion zu maximieren, ist es zweckmäßig, zuerst den Prologarithmus zu verwenden (der Logarithmus der Funktion erreicht sein Maximum an derselben Stelle wie die Funktion selbst):

$$

$$f (x) = ln (\ prod_ {i \ in [1, m]} {\ frac {1} {\ sigma \ sqrt {2 \ pi}} \; e ^ {- \ frac {(b_i-a_ix ) ^ 2} {2 \ sigma ^ 2}}}) = \ sum_ {i \ in [1, m]} ln \ frac {1} {\ sigma \ sqrt {2 \ pi}} \; - \ sum_ {i \ in [1, m]} \ frac {(b_i-a_ix) ^ 2} {2 \ sigma ^ 2}$$

Was wiederum darauf hinausläuft, die folgende Funktion zu minimieren:

$$

$$f (x) = \ sum_ {i \ in [1, m]} (b_i-a_ix) ^ 2$$

Dies wird übrigens als Methode der kleinsten Quadrate bezeichnet. Oft werden alle oben genannten Überlegungen weggelassen und diese Methode wird einfach verwendet.

QR-Zersetzung

Das Minimum der obigen Funktion kann gefunden werden, wenn Sie den Punkt finden, an dem der Gradient dieser Funktion gleich Null ist. Und der Farbverlauf wird wie folgt geschrieben:

$$

$$\ nabla f (x) = \ sum_ {i \ in [1, m]} 2a_i (a_ix - b_i) = 0$$

Die QR-Zerlegung ist eine Matrixmethode zur Lösung des Minimierungsproblems, das bei der Methode der kleinsten Quadrate verwendet wird. In dieser Hinsicht schreiben wir die Gleichung in Matrixform um:

$$

$$A ^ T A x = A ^ Tb$$

Also legen wir die Matrix an $$$A$auf Matrizen $$$Q$und $$$R$und führen Sie eine Reihe von Transformationen durch (der QR-Zerlegungsalgorithmus selbst wird hier nicht berücksichtigt, sondern nur seine Verwendung in Bezug auf die Aufgabe):

$$

$$\ begin {align} & (QR) ^ T (QR) x = (QR) ^ Tb; \\ & R ^ T Q ^ T Q R x = R ^ T Q ^ T b; \\ \ end {align}$$

Matrix $$$Q$ist orthogonal. Dies ermöglicht es uns, die Arbeit loszuwerden. $$$Q Q ^ T$::

$$

$$\ begin {align} & R ^ T R x = R ^ T Q ^ T b; \\ & (R ^ T) ^ {- 1} R ^ T R x = (R ^ T) ^ {- 1} R ^ T Q ^ T b; \\ & R x = Q ^ T b. \ end {align}$$

Und wenn Sie ersetzen $$$Q ^ T b$auf $$$z$es wird sich herausstellen $$$R x = z$. Angesichts dessen $$$R$ist die obere Dreiecksmatrix, es sieht so aus:

$$

$$\ begin {pmatrix} r_ {11} & r_ {12} & r_ {13} & r_ {14} & ... & r_ {1n} \\ 0 & r_ {22} & r_ {23} & r_ { 24} & ... & r_ {2n} \\ 0 & 0 & r_ {33} & r_ {34} & ... & r_ {3n} \\ 0 & 0 & 0 & r_ {44} & .. . & r_ {4n} \\ ... \\ 0 & 0 & 0 & 0 & ... & r_ {nn} \\ \ end {pmatrix} \ times \ begin {pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ ... \\ x_n \ end {pmatrix} = \ begin {pmatrix} z_1 \\ z_2 \\ z_3 \\ z_4 \\ ... \\ z_n \ end {pmatrix}$$

Dies kann durch die Substitutionsmethode gelöst werden. Artikel $$$x_n$ist wie $$$z_n / r_ {nn}$vorheriger Artikel $$$x_ {n-1}$ist wie $$$(z_ {n-1} - r_ {n-1, n} x_n) / r_ {n-1, n-1}$usw.

Es ist hier anzumerken, dass die Komplexität des resultierenden Algorithmus durch die Verwendung der QR-Zerlegung ist $$$O (2mn ^ 2)$. Darüber hinaus ist es trotz der Tatsache, dass die Matrixmultiplikationsoperation gut parallelisiert ist, nicht möglich, eine effektive verteilte Version dieses Algorithmus zu schreiben.

Gefälle Abstieg

Wenn man über die Minimierung einer bestimmten Funktion spricht, lohnt es sich immer, an die Methode des (stochastischen) Gradientenabfalls zu erinnern. Dies ist eine einfache und effektive Minimierungsmethode, bei der der Gradient einer Funktion an einem Punkt iterativ berechnet und dann auf die dem Gradienten gegenüberliegende Seite verschoben wird. Jeder dieser Schritte bringt die Lösung auf ein Minimum. Der Farbverlauf sieht gleich aus:

$$

$$\ nabla f (x) = \ sum_ {i \ in [1, m]} 2a_i (a_ix - b_i)$$

Diese Methode ist aufgrund der linearen Eigenschaften des Gradientenoperators auch gut parallelisiert und verteilt. Beachten Sie, dass in der obigen Formel unabhängige Begriffe unter dem Vorzeichen der Summe stehen. Mit anderen Worten, wir können den Gradienten unabhängig für alle Indizes berechnen $$$i$von zuerst bis $$$k$Berechnen Sie parallel dazu den Gradienten für Indizes mit $$$k + 1$vorher $$$m$. Fügen Sie dann die resultierenden Verläufe hinzu. Das Ergebnis der Addition ist das gleiche, als hätten wir sofort den Gradienten für die Indizes vom ersten bis zum berechnet $$$m$. Wenn also die Daten auf mehrere Teile der Daten verteilt sind, kann der Gradient für jeden Teil unabhängig berechnet werden, und dann können die Ergebnisse dieser Berechnungen summiert werden, um das Endergebnis zu erhalten:

$$

$$\ nabla f (x) = \ sum_ {i \ in P_1} 2a_i (a_ix - b_i) + \ sum_ {i \ in P_2} 2a_i (a_ix - b_i) + ... + \ sum_ {i \ in P_k} 2a_i (a_ix - b_i)$$

In Bezug auf die Implementierung passt dies in das MapReduce- Paradigma. Bei jedem Schritt des Gradientenabfalls wird eine Aufgabe zum Berechnen des Gradienten an jeden Datenknoten gesendet, dann werden die berechneten Gradienten zusammen gesammelt und das Ergebnis ihrer Summierung wird verwendet, um das Ergebnis zu verbessern.

Trotz der Einfachheit der Implementierung und der Fähigkeit, das MapReduce-Paradigma auszuführen, hat der Gradientenabstieg auch seine Nachteile. Insbesondere ist die Anzahl der Schritte, die erforderlich sind, um eine Konvergenz zu erreichen, im Vergleich zu anderen spezialisierteren Methoden erheblich größer.

LSQR

LSQR ist eine weitere Methode zur Lösung des Problems, die sowohl zur Rekonstruktion der linearen Regression als auch zur Lösung linearer Gleichungssysteme geeignet ist. Das Hauptmerkmal ist, dass es die Vorteile von Matrixmethoden und einen iterativen Ansatz kombiniert. Implementierungen dieser Methode finden Sie sowohl in der SciPy- Bibliothek als auch in MATLAB . Eine Beschreibung dieser Methode wird hier nicht gegeben (sie ist im LSQR- Artikel zu finden : Ein Algorithmus für spärliche lineare Gleichungen und spärliche kleinste Quadrate ). Stattdessen wird ein Ansatz demonstriert, um den LSQR an die Ausführung in einer verteilten Umgebung anzupassen.

Die LSQR-Methode basiert auf dem Bidiagonalisierungsverfahren. Dies ist eine iterative Prozedur, deren Iteration aus den folgenden Schritten besteht:


Aber basierend auf der Tatsache, dass die Matrix $$$A$horizontal partitioniert, kann jede Iteration als MapReduce in zwei Schritten dargestellt werden. Somit ist es möglich, die Datenübertragungen während jeder Iteration zu minimieren (nur Vektoren mit einer Länge, die der Anzahl der Unbekannten entspricht):



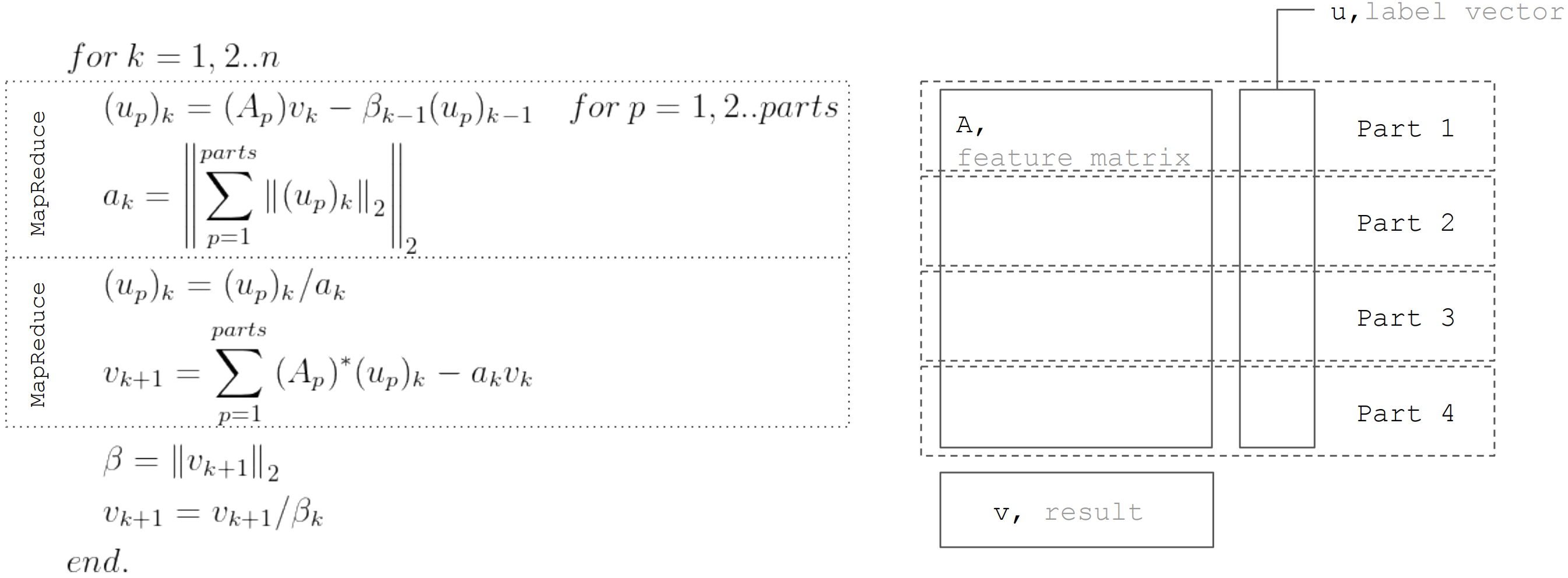
Dieser Ansatz wird bei der Implementierung der linearen Regression in Apache Ignite ML verwendet .

Fazit

Es gibt viele lineare Regressionswiederherstellungsalgorithmen, aber nicht alle können unter allen Bedingungen angewendet werden. Die QR-Zerlegung eignet sich daher hervorragend für eine genaue Lösung kleiner Arrays. Der Gradientenabstieg wird einfach implementiert und ermöglicht es Ihnen, schnell eine ungefähre Lösung zu finden. Und LSQR kombiniert die besten Eigenschaften der beiden vorherigen Algorithmen, da es verteilt werden kann, im Vergleich zum Gradientenabstieg schneller konvergiert und im Gegensatz zur QR-Zerlegung auch ein vorzeitiges Stoppen des Algorithmus ermöglicht, um eine ungefähre Lösung zu finden.