In den meisten Konstruktionssystemen (CAD) ist die Hauptdarstellung des simulierten Objekts die Grenzdarstellung der Geometrie oder B-rep (Grenzdarstellung). CAD-Benutzer müssen sich jedoch zunehmend mit Polygonmodellen auseinandersetzen, die beispielsweise durch 3D-Scannen erhalten oder aus Online-Katalogen ausgeliehen wurden.
Damit sie für weitere Arbeiten geeignet sind, müssen Sie das Polygonnetz in ein B-Rep-Modell konvertieren. Und das ist gar nicht so einfach.
Wir haben die Softwarekomponente C3D B-Shaper entwickelt, die in das Designsystem integriert ist und polygonale Modelle in eine Grenzdarstellung konvertiert. In diesem Beitrag zeigen wir den Konvertierungsalgorithmus und Implementierungsbeispiele in C ++.




Was ist das Hauptproblem von polygonalen Modellen in Bezug auf CAD? Herkömmliche Werkzeuge können nicht auf sie angewendet werden - um Boolesche Operationen auszuführen, Fasen und Verrundungen zu konstruieren, Projektionen und Schnitte zu erhalten. Wenn die Verwendung des B-rep-Modells zum Erstellen seiner polygonalen Darstellung recht einfach ist (dies erfolgt mithilfe der Triangulation), ist die inverse Transformation viel schwieriger. Es treten eine Reihe von Problemen auf - die Erkennung von Oberflächen verschiedener Typen (einschließlich Freiformflächen), das Vorhandensein von Rauschen, die beispielsweise für 3D-Scanergebnisse charakteristisch sind.

Im neuen SDK haben wir einen dreistufigen Mechanismus zur Umwandlung des polygonalen Modells in B-rep implementiert: Segmentierung, Oberflächenrekonstruktion, Konstruktion des B-rep-Modells. Im Allgemeinen wird angenommen, dass der Prozess iterativ ist: Wenn der Benutzer aus irgendeinem Grund mit dem Ergebnis nicht zufrieden ist, kann er die erforderlichen Korrekturänderungen in den Phasen der Segmentierung und Rekonstruktion von Oberflächen vornehmen.


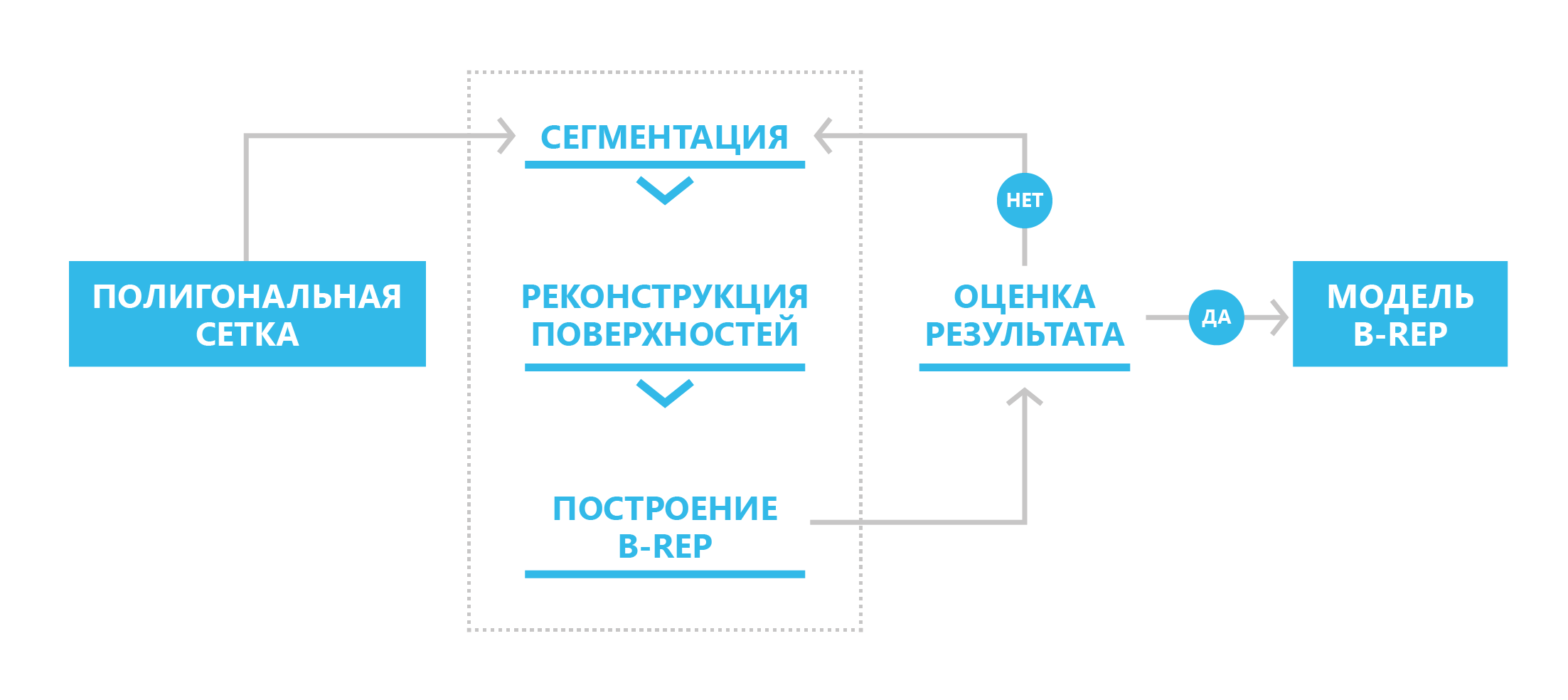Das Schema zum Konvertieren einer polygonalen Darstellung in eine Grenze

Bevor der Konvertierungsprozess in B-rep eingeleitet wird, muss in einigen Fällen die Qualität des ursprünglichen Polygonnetzes verbessert werden: Koordinieren Sie die Richtungen der Normalen an benachbarten Polygonen, beseitigen Sie „Löcher“ und wenden Sie Glättungsalgorithmen an, wenn im ursprünglichen Netz Rauschen vorhanden ist.

Polygonsegmentierung

In der ersten Phase wird der anfängliche Satz von Netzpolygonen in Teilmengen (Segmente) klassifiziert. Informationen über die Normalen an den Eckpunkten des Netzes ermöglichen eine Segmentierung erster Ordnung und stellen dadurch die anfängliche Netzaufteilung sicher sowie die Klassifizierung flacher oder stark gekrümmter Bereiche.

Die anfängliche Vernetzung basiert auf der Definition von sogenannten "scharfen" Kanten - solchen Kanten zwischen zwei dreieckigen Polygonen, deren Winkel zwischen den durchschnittlichen Normalen einen bestimmten vorbestimmten Wert überschreitet.

Die Segmentierung zweiter Ordnung analysiert das Gitter gemäß seinen Hauptkrümmungen, was eine ausreichende Grundlage für die Klassifizierung von Elementarflächen bietet. Bei der Berechnung der Krümmungen an den Eckpunkten des Gitters verwendeten wir die Ergebnisse von Mayer (Mark Meyer, Mathieu Desbrun, Peter Schroder und Alan H. Barr, Operatoren für diskrete Differentialgeometrie für dreieckige 2-Mannigfaltigkeiten, Visualisierung und Mathematik III, 2003), um das diskrete Differential zu bestimmen Operator für triangulierte Bereiche: Für jeden Scheitelpunkt des ursprünglichen Netzes betrachten wir eine Reihe benachbarter Scheitelpunkte, die einem bestimmten Scheitelpunkt durch eine Kante zugeordnet sind. Dann wird ein diskreter Operator K für einen gegebenen Scheitelpunkt berechnet, auf dessen Grundlage die durchschnittliche Normal-, durchschnittliche K _{H -} und Gaußsche K _G -Krümmung am Scheitelpunkt des Gitters bestimmt werden.


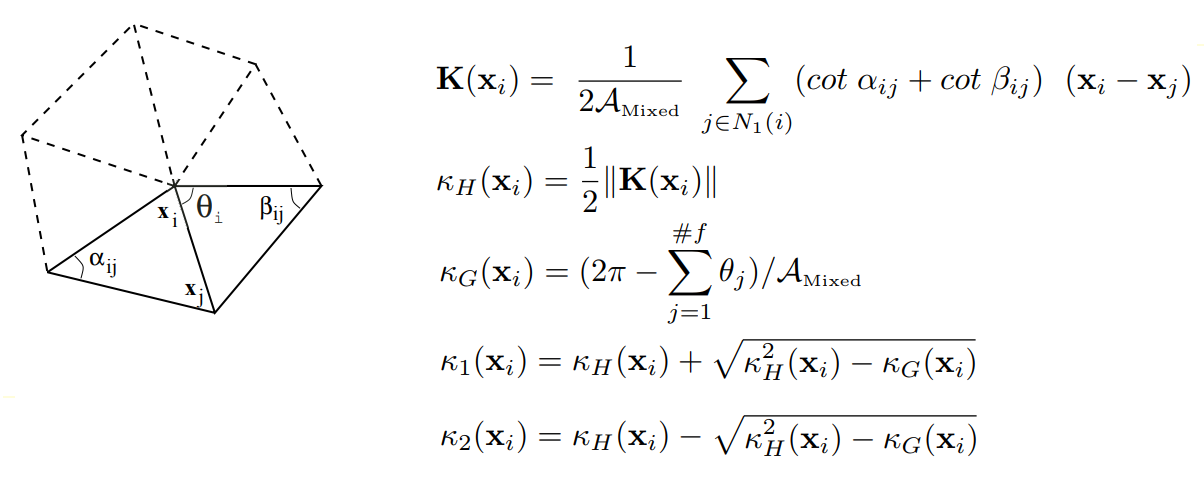Zur Definition eines diskreten Differentialoperators für triangulierte Domänen

Somit wird der Krümmungstensor für jeden Scheitelpunkt des Gitters berechnet, dessen Eigenwerte die gewünschten Hauptkrümmungen K ₁ und K _{2 sind} , und die Eigenvektoren sind die Hauptrichtungen der Krümmungsänderung.

Als nächstes werden die Maschenscheitelpunkte gemäß den darin berechneten Werten der Hauptkrümmungen K ₁ und K ₂ klassifiziert. Der Scheitelpunktklassifizierungsalgorithmus basiert auf dem k-Mittelwert-Verfahren, d. H. Auf der Minimierung der gesamten quadratischen Abweichung von Clusterpunkten von den Zentren dieser Cluster. Infolgedessen ist am Ausgang des Algorithmus jeder Scheitelpunkt des Gitters einem bestimmten Cluster zugeordnet $$$Ci$und ein Paar von Krümmungen (Cluster-Zentrum) (L. Guillaume, "Curvature Tensor Based Triangle Mesh Segmentation with Boundary Rectification", Proceedings Computer Graphics International (CGI), 2004).


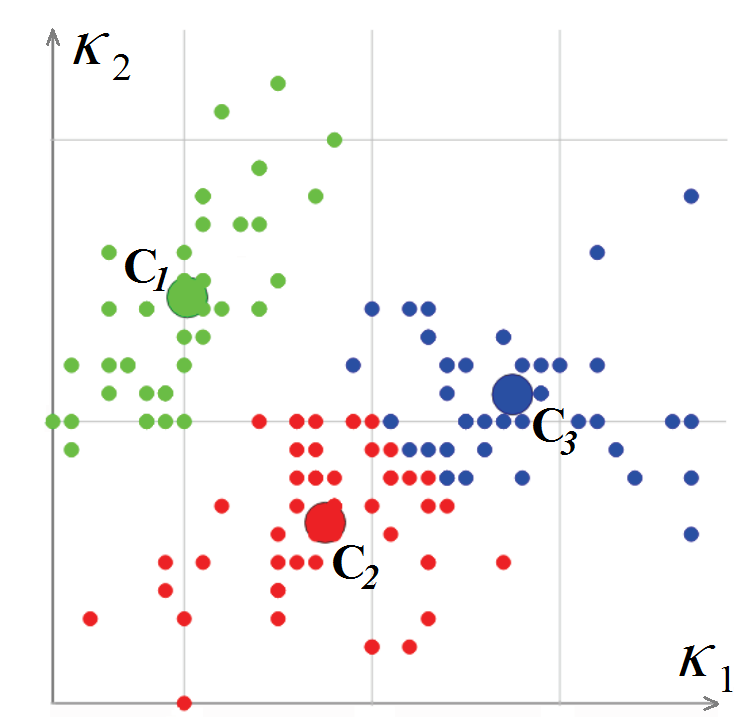Klassifizierung der Eckpunkte eines Polygonnetzes im Krümmungsraum

Nach dem Klassifizieren der Eckpunkte des Polygonnetzes müssen die Polygone klassifiziert werden. Zu Beginn dieses Vorgangs wird ein dreieckiges Polygon ausgewählt, für das die Krümmung als vollständig definiert betrachtet werden kann (alle drei Eckpunkte gehören zu einem Cluster oder zwei Eckpunkte liegen auf einer scharfen Kante). Dieses Polygon wird als neues Segment deklariert, und die rekursive Prozedur zum Erweitern des Segments beginnt damit: Für jedes dreieckige Polygon werden die angrenzenden Polygone berücksichtigt, sofern die Kante zwischen ihnen nicht „scharf“ ist.

Wenn der Scheitelpunkt eines benachbarten Polygons gegenüber der gemeinsamen Kante auf einer scharfen Kante liegt oder zum selben Cluster gehört, wird dieses Polygon dem Segment hinzugefügt. Der Vorgang wird wiederholt, bis alle Polygone dieses Rasters angezeigt werden. So sieht der implementierte Netzsegmentierungsmechanismus aus.


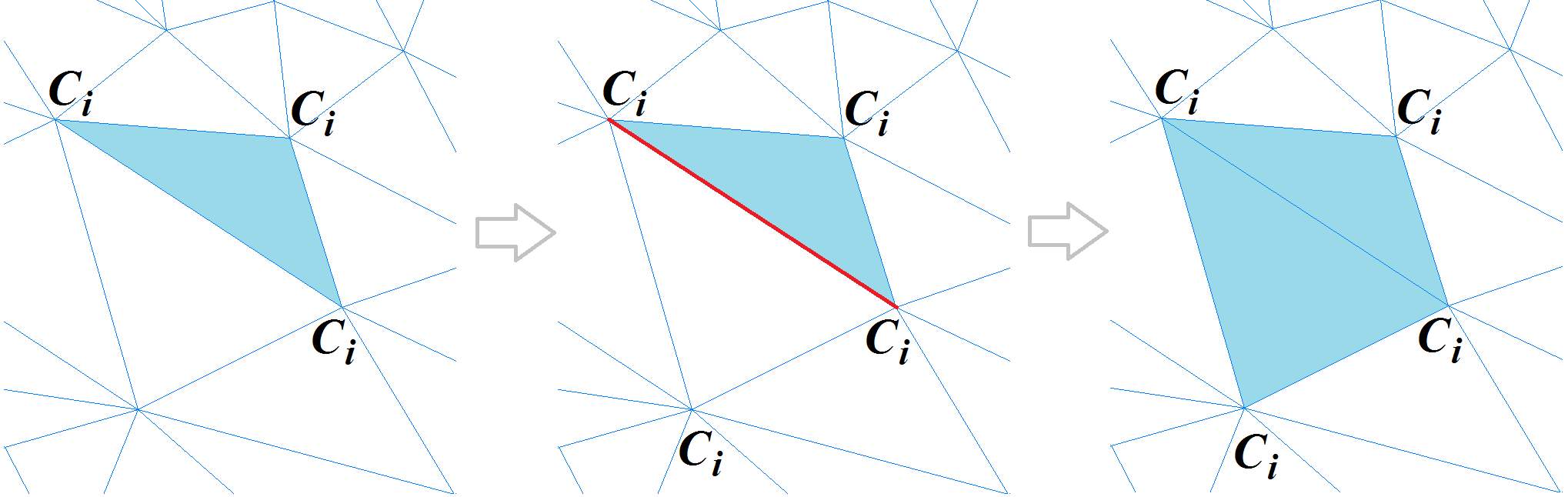Segmentierungsmechanismus für Polygonnetze

Am Ende des Segmentbildungsvorgangs wird ein spezieller Algorithmus zum Zusammenfügen benachbarter Segmente durchgeführt, um eine übermäßige Segmentierung des betreffenden Netzes zu vermeiden.

Oberflächenerkennung

In der zweiten Stufe muss jedem der Segmente eine bestimmte Oberfläche zugeordnet werden, die sich ihrer Form mit einer bestimmten Genauigkeit annähert. Zunächst bestimmen die Werte der Hauptkrümmungen für ein bestimmtes Segment die Möglichkeit, die Form eines Segments durch eine Elementarfläche zu beschreiben:

• Ebene: k ₁ = k ₂ = 0
• Kugel: k ₁ = k ₂ = K > 0
• Zylinder: k ₁ = K > 0, k ₂ = 0
• Kegel: k ₁ ∈ [ a , b ], k ₂ = 0
• Torus: k ₁ = K , k ₂ ∈ [ a , b ]

Wenn keine der Elementarflächen zur Beschreibung eines Segments geeignet ist, versucht der Algorithmus, die Extrusions- oder Rotationsfläche zu erkennen. Wenn es letztendlich nicht möglich war, eine analytische Oberfläche zur Beschreibung der Form des Segments auszuwählen, wird eine NURBS-Oberfläche dafür erstellt.

Elementare Oberflächen werden mithilfe von Methoden zum Anpassen einfacher geometrischer Objekte an eine Reihe von Punkten erstellt. Um den Kreis und die Kugel anzupassen, wird die Methode der kleinsten Quadrate verwendet, um die Ebene anzupassen - die Hauptkomponentenmethode. Jede rekonstruierte Oberfläche wird auf Übereinstimmung mit einem Segment für eine gegebene Erkennungsgenauigkeit überprüft.

Aus Gründen der Klarheit haben wir die erkannten Oberflächen in verschiedenen Farben lackiert: Ebenen - blau, Zylinder - rot, Kugeln - grün, Kegel - gelb, tori - lila.


Originales Polygonnetz (links) und segmentiertes Netz (rechts) mit auf Segmenten erkannten Flächen

Erstellen eines B-rep-Modells

Die letzte Stufe der Transformation ist die Konstruktion eines B-rep-Modells basierend auf der Segmentierung der erkannten Oberflächen. Bei diesem Ansatz wird ein Graph benachbarter Regionen auf der Basis segmentierter Regionen erstellt, der die Topologie des Modells widerspiegelt und als Grundlage für die Erstellung des endgültigen B-rep-Modells dient.

Im Gegensatz zu den vorherigen Konvertierungsstufen erfolgt die B-Rep-Montage in einem vollautomatischen Modus: Die Schnittlinien benachbarter rekonstruierter Oberflächen werden gefunden, die Kanten der Flächen werden darauf aufgebaut, die Flächen selbst und schließlich wird die B-Rep-Schale zusammengebaut.




Originales Polygonnetz (links) und B-Rep-Modell (rechts)

Es ist jedoch nicht immer möglich, eine topologisch korrekte Schale zu konstruieren. Nehmen wir als Beispiel für eine solche Situation an, dass wir während der Rekonstruktion von Oberflächen zwei Oberflächen haben - einen Zylinder und eine Ebene, und ihre Position im Raum nahe an der Tangente liegt. Aufgrund von Fehlern bei der Rekonstruktion der Oberflächen ihrer Schnittpunkte gibt es möglicherweise überhaupt keine. In solchen Fällen kann die Schale mit einigen Fehlern aufgebaut sein, die der Benutzer durch ordnungsgemäßes Anpassen der Oberflächenparameter beheben kann.

Arten von polygonalen Modellen und die Wahl des Konvertierungsmodus

Heute gibt es in der polygonalen Darstellung mehrere Hauptquellen für Modelle:

• Online-Kataloge, Datenbanken von 3D-Modellen im Polygonformat (STL, VRML, OBJ), z. B. 3D Warehouse, Cults 3D usw.
• 3D-Scan-Ergebnisse
• Ergebnisse der topologischen Modelloptimierung durch CAE-Algorithmen.

Polygonale Modelle aus diesen Quellen können in zwei Gruppen unterteilt werden: Das erste umfasst Modelle, die Triangulationen von B-rep-Objekten sind, und das zweite - alle anderen. Die charakteristischen Unterschiede der ersten Gruppe sind das Fehlen von Rauschen im Polygonnetz und das Überwiegen analytisch definierter Oberflächen. Daher erfolgt die Umstellung auf die B-rep-Modelle aus der ersten Gruppe entweder im vollautomatischen Modus oder mit minimalem Benutzereingriff.

Polygonale Gitter der Modelle der zweiten Gruppe implizieren eine dichtere interaktive Interaktion mit dem Benutzer. Aus diesem Grund haben wir im C3D B-Shaper zunächst zwei Betriebsarten festgelegt - vollautomatisch und interaktiv.

Die Wahl eines bestimmten Modus hängt auch vom Zweck der Transformation ab: In einigen Fällen kann die topologische Konnektivität der Elemente der resultierenden Schale sowie deren Richtigkeit vernachlässigt werden. Ein solcher Ansatz ist beispielsweise akzeptabel, um das Rendern in einer BIM-Anwendung zu optimieren, wenn der Benutzer dem aktuellen Modell des Raums beliebige Innenelemente hinzufügen kann. Andererseits ist es für Reverse Engineering-Aufgaben erforderlich, die genaueste Kopie des Originalmodells zu erhalten, um beispielsweise die Ausrichtung der Zylinder mit einer bestimmten Genauigkeit beizubehalten, die tangentiale Position eines Oberflächenpaares sicherzustellen und infolgedessen die korrekte Topologie des Modells zu erhalten. In diesem Fall können Sie nicht ohne Benutzereingriff auskommen Konvertierungsprozess.

Die automatische Konvertierungsschnittstelle C3D B-Shaper wird durch die folgenden Funktionen dargestellt, die das Eingaberaster und die Konvertierungseinstellungen als Eingabe akzeptieren:

MbResultType ConvertMeshToShell( MbMesh & mesh, MbFaceShell *& shell, const MbMeshProcessorValues & params ); MbResultType ConvertCollectionToShell( MbCollection & collection, MbFaceShell *& shell, const MbMeshProcessorValues & params ); 

Die Konvertierungseinstellungen umfassen den Erkennungsgenauigkeitswert, d.h. der maximal zulässige Abstand der Eckpunkte des Polygonnetzes innerhalb der Grenzen dieses Segments zur erkannten Oberfläche. Diese Genauigkeit kann absolut oder relativ sein: Bei Verwendung der relativen Genauigkeit wird die Abweichung der Flächen des Körpers vom Raster in Bezug auf die Größe des Modells überprüft.

Der Benutzer hat auch die Möglichkeit, den Erkennungsmodus zu wechseln, wodurch Sie die Oberflächentypen während der Rekonstruktion steuern können.
Die MbMeshProcessor-Klassenschnittstelle bietet erweiterte Funktionen zum Verwalten von Segmentierungs- und Oberflächenerkennungsprozessen:

 class MbMeshProcessor { .. public: // “” . void SetUseMeshSmoothing( bool useSmoothing ); //   . const MbCollection & GetSegmentedMesh(); MbResultType SegmentMesh( bool createSurfaces = true ); void ResetSegmentation(); void UniteSegments( size_t firstSegmentIdx, size_t secondSegmentIdx ); MbResultType SegmentMeshBySeparators( const std::vector<std::vector<uint>> & sep ); //   . void FitSurfaceToSegment( size_t idxSegment ); void FitSurfaceToSegment( size_t idxSegment, MbeSpaceType surfaceType ); const MbSurface * GetSegmentSurface( size_t idxSegment ) const; //  B-rep . MbResultType CreateBRepShell( MbFaceShell *& pShell ); .. } 

Um beispielsweise die Ergebnisse der automatischen Segmentierung zu korrigieren, werden Werkzeuge zum Kombinieren, Trennen usw. von Segmenten bereitgestellt. Der Benutzer kann eine Oberfläche eines bestimmten Typs in ein Segment eingeben sowie Parameter für eine bereits erkannte Oberfläche ändern.

Was passiert jetzt?

Im Juli haben wir die erste Version der Komponente veröffentlicht und entwickeln sie nun in mehreren Bereichen weiter: automatische Segmentierungsalgorithmen, Werkzeuge zur Segmentierungsbearbeitung, Erstellen von Freiformflächen (NURBS) basierend auf einem Segment, Verbesserung der Verarbeitungsqualität von B-Rep-Shells.

Interessierte Entwickler können den C3D B-Shaper testen. Die Komponente wird auf Anfrage auf unserer Website drei Monate lang kostenlos zur Verfügung gestellt.

Autor - Andrey Tumanin, Ph.D., Mathematiker-Programmierer von C3D Labs