
Eine der wertvollsten Ressourcen eines sozialen Netzwerks ist das „Diagramm der Freundschaften“ - Informationen werden über Verbindungen in dieser Spalte verbreitet, interessante Inhalte werden an Benutzer gesendet und konstruktives Feedback wird an Inhaltsautoren gesendet. Gleichzeitig ist das Diagramm eine wichtige Informationsquelle, mit der Sie den Benutzer besser verstehen und den Dienst kontinuierlich verbessern können. In diesen Fällen, in denen das Diagramm wächst, ist es jedoch technisch immer schwieriger, Informationen daraus zu extrahieren. In diesem Artikel werden wir über einige Tricks sprechen, die zum Verarbeiten großer Diagramme in OK.ru verwendet werden.
Betrachten Sie zunächst eine einfache Aufgabe aus der realen Welt: Bestimmen Sie das Alter des Benutzers. Wenn Sie das Alter kennen, kann das soziale Netzwerk relevantere Inhalte auswählen und sich besser an die Person anpassen. Es scheint, dass das Alter bereits beim Erstellen einer Seite in sozialen Netzwerken angegeben wird, aber tatsächlich sind Benutzer häufig gerissen und geben ein anderes Alter als das tatsächliche an. Ein sozialer Graph kann helfen, die Situation zu korrigieren :).
Nehmen wir zum Beispiel Bob (alle Charaktere im Artikel sind fiktiv, jeder Zufall mit der Realität ist das Ergebnis der Kreativität eines zufälligen Hauses):

Einerseits sind die Hälfte von Bobs Freunden Teenager, was darauf hindeutet, dass Bob auch ein Teenager ist. Er hat aber auch ältere Freunde, so dass das Vertrauen in die Antwort gering ist. Zusätzliche Informationen aus dem sozialen Diagramm können helfen, die Antwort zu verdeutlichen:

Wenn wir nicht nur die Bögen berücksichtigen, an denen Bob direkt beteiligt ist, sondern auch die Bögen zwischen seinen Freunden, können wir sehen, dass Bob Teil einer dichten Gemeinschaft von Jugendlichen ist, die es uns ermöglicht, mit größerem Vertrauen eine Schlussfolgerung über sein Alter zu ziehen.
Eine solche Datenstruktur ist als Ego-Netzwerk oder Ego-Subgraph bekannt und wird seit langem erfolgreich zur Lösung vieler Probleme eingesetzt: Suche nach Communitys, Identifizierung von Bots und Spam, Empfehlungen von Freunden und Inhalten usw. Die Berechnung des Ego eines Untergraphen für alle Benutzer in einem Diagramm mit Hunderten von Millionen Knoten und Dutzenden von Milliarden Bögen ist jedoch mit einer Reihe von "kleinen technischen Schwierigkeiten" behaftet :).
Das Hauptproblem besteht darin, dass bei der Betrachtung von Informationen über den "zweiten Schritt" in der Grafik eine quadratische Explosion der Anzahl der Verbindungen auftritt. Beispielsweise kann für einen Benutzer mit 150 direkten Ego-Links ein Untergraph bis zu bis enthalten 150+150∗149/2=$11.32 Links und für einen aktiven Benutzer mit 5.000 Freunden kann der Ego-Untergraph auf mehr als 12.000.000 Links anwachsen.
Eine zusätzliche Komplikation ist die Tatsache, dass das Diagramm in einer verteilten Umgebung gespeichert ist und kein Knoten ein vollständiges Bild des Diagramms im Speicher hat. Die Arbeit an einer ausgewogenen Partitionierung von Graphen wird sowohl in der Akademie als auch in der Industrie durchgeführt, aber selbst die besten Ergebnisse beim Sammeln des Ego-Subgraphen führen zu einer "Alles mit allen" -Kommunikation: Um Informationen über die Freunde der Freunde des Benutzers zu erhalten, müssen Sie zu allen "Partitionen" gehen. in den meisten Fällen.
Eine der funktionierenden Alternativen in diesem Fall ist die erzwungene Duplizierung von Daten (z. B. Algorithmus 3 in einem Artikel von Google ). Diese Duplizierung ist jedoch auch nicht kostenlos. Versuchen wir herauszufinden, was in diesem Prozess verbessert werden kann.
Naiver Algorithmus
Betrachten Sie zunächst den „naiven“ Algorithmus zum Generieren eines Ego-Subgraphen:

Der Algorithmus nimmt an, dass der ursprüngliche Graph als Adjazenzliste gespeichert ist, d.h. Informationen zu allen Freunden des Benutzers werden in einem einzigen Datensatz mit der Benutzer-ID im Schlüssel und der Liste der Freunde-ID im Wert gespeichert. Um den zweiten Schritt zu machen und Informationen über Freunde zu erhalten, benötigen Sie:
- Konvertieren Sie ein Diagramm in die Liste der Kanten, wobei jede Kante ein separater Eintrag ist.
- Stellen Sie sicher, dass die Liste der Kanten sich selbst verbindet, wodurch alle Pfade in einem Diagramm der Länge 2 angezeigt werden.
- Nach Pfadanfang gruppieren.
Bei der Ausgabe für jeden Benutzer erhalten wir Listen mit Pfaden der Länge 2 für jeden Benutzer. Es sollte hier angemerkt werden, dass die resultierende Struktur tatsächlich eine zweistufige Nachbarschaft des Benutzers ist , während der Ego-Untergraph seine Teilmenge ist. Um den Vorgang abzuschließen, müssen wir daher alle Bögen herausfiltern, die außerhalb der unmittelbaren Freunde liegen.
Dieser Algorithmus ist gut, da er in zwei Zeilen auf Scala unter Apache Spark implementiert ist. Aber die Vorteile enden hier: Für ein Diagramm der industriellen Größe liegt das Volumen der Netzwerkkommunikation über dem Grenzwert und die Betriebszeit wird in Tagen gemessen. Die Hauptschwierigkeit entsteht durch zwei Shuffle-Operationen, die beim Verbinden und Gruppieren auftreten. Ist es möglich, die Menge der gesendeten Daten zu reduzieren?
Ego-Subgraph in einem Shuffle
Da unser Diagramm der Freundschaften symmetrisch ist, können Sie die von Tomas Schank vorgeschlagenen Optimierungen verwenden:
- Sie können alle Pfade der Länge 2 ohne Verbindung erhalten - wenn Bob Freunde Alice und Harry hat, gibt es Alice-Bob-Harry- und Harry-Bob-Alice-Pfade.
- Bei der Gruppierung entsprechen zwei Pfade am Eingang derselben neuen Kante. Der Pfad Bob-Alice-Dave und Bob-Dave-Alice enthält dieselben Informationen für Bob. Dies bedeutet, dass Sie nur jeden zweiten Pfad senden können, indem Sie Benutzer nach ihrer ID sortieren.
Nach dem Anwenden der Optimierungen sieht das Arbeitsschema folgendermaßen aus:

- In der ersten Phase der Generierung erhalten wir eine Liste von Pfaden der Länge 2 mit einem Filter der Auftrags-ID.
- Beim zweiten gruppieren wir nach dem ersten Benutzer auf dem Weg.
In dieser Einstellung erfüllt der Algorithmus eine Mischoperation, und die Größe der über das Netzwerk übertragenen Daten wird halbiert. :) :)
Legen Sie den Ego-Untergraphen in Erinnerung
Ein wichtiges Thema, das wir noch nicht in Betracht gezogen haben, ist die Zerlegung der Daten im Ego eines Untergraphen in den Speicher. Um das Diagramm als Ganzes zu speichern, haben wir eine Adjazenzliste verwendet. Diese Struktur eignet sich für Aufgaben, bei denen das fertige Diagramm als Ganzes durchlaufen werden muss. Sie ist jedoch teuer, wenn Sie ein Diagramm aus Teilen erstellen und subtilere Analysen durchführen möchten. Die ideale Struktur für unsere Aufgabe sollte effektiv die folgenden Operationen ausführen:
- Die Vereinigung zweier Graphen aus verschiedenen Partitionen.
- Alle menschlichen Freunde bekommen.
- Überprüfen, ob zwei Personen verbunden sind.
- Speicherung im Speicher ohne Boxaufwand.
Eines der am besten geeigneten Formate für diese Anforderungen ist das Analogon einer spärlichen CSR-Matrix :
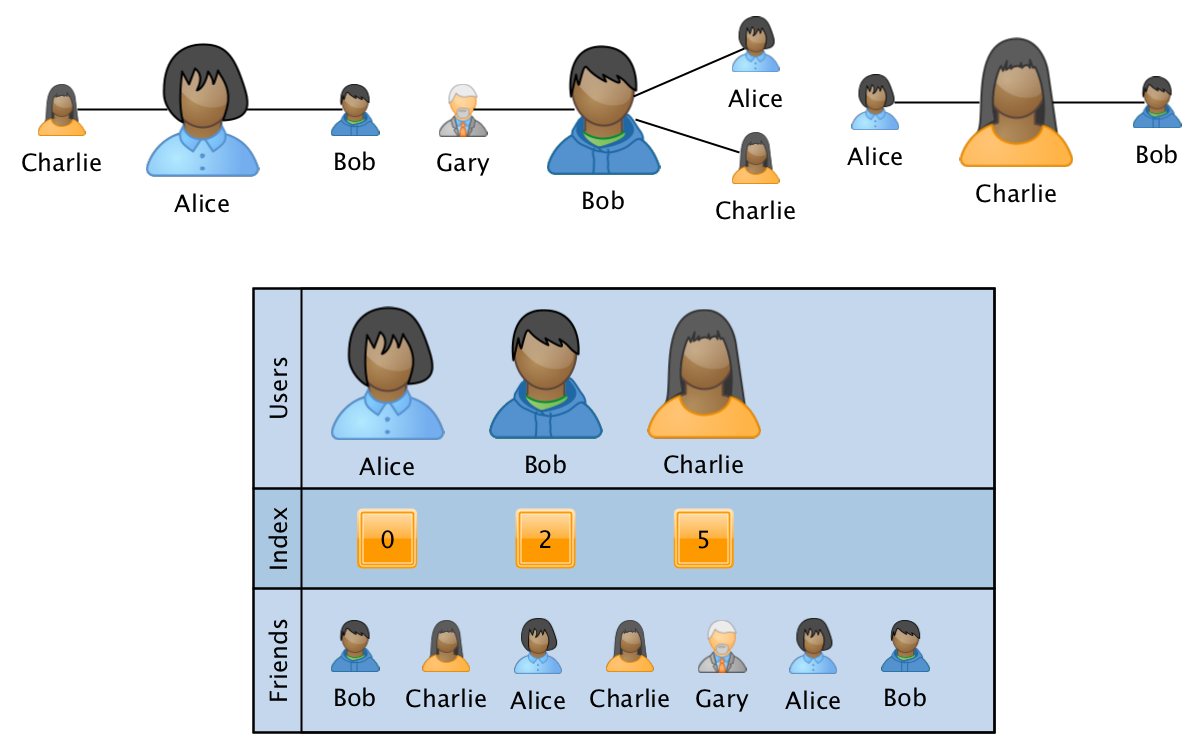
Das Diagramm wird in diesem Fall in Form von drei Arrays gespeichert:
- Benutzer - Ein sortiertes Array mit der ID aller Benutzer, die am Diagramm teilnehmen.
- index - Ein Array mit der gleichen Größe wie Benutzer, in dem für jeden Benutzer ein Indexzeiger auf den Beginn von Informationen zu Benutzerbeziehungen im dritten Array gespeichert ist.
- Freunde - Ein Array mit einer Größe, die der Anzahl der Kanten im Diagramm entspricht, wobei die IDs verwandter Benutzer nacheinander für die entsprechenden IDs von Benutzern angezeigt werden. Das Array ist nach Verarbeitungsgeschwindigkeit innerhalb der Informationen über die Links eines einzelnen Benutzers sortiert.
In diesem Format wird die Operation zum Zusammenführen von zwei Graphen in linearer Zeit ausgeführt und die Operation zum Abrufen von Informationen über einen bestimmten Benutzer oder über ein Benutzerpaar pro Logarithmus der Anzahl der Eckpunkte. In diesem Fall hängt der Overhead im Speicher nicht von der Größe des Diagramms ab, da eine feste Anzahl von Arrays verwendet wird. Durch Hinzufügen eines vierten Datenarrays mit einer Größe, die der Größe von Freunden entspricht, können Sie zusätzliche Informationen speichern, die mit den Beziehungen im Diagramm verknüpft sind.
Unter Verwendung der Graphensymmetrieeigenschaft kann nur die Hälfte der "oberen dreieckigen" Bögen gespeichert werden (wenn Bögen nur von einer kleineren ID zu einer größeren ID gespeichert werden). In diesem Fall dauert die Rekonstruktion aller Verbindungen eines einzelnen Benutzers jedoch linear. Ein guter Kompromiss in diesem Fall kann ein Ansatz sein, der eine "obere dreieckige" Codierung zum Speichern und Übertragen zwischen Knoten und eine symmetrische Codierung beim Laden des Ego des Subgraphen in den Speicher zur Analyse verwendet.
Shuffle reduzieren
Selbst nach der Implementierung aller oben genannten Optimierungen funktioniert die Aufgabe, alle Ego-Untergraphen zu erstellen, noch zu lange. In unserem Fall ca. 6 Stunden bei hoher Auslastung des Clusters. Ein genauerer Blick zeigt, dass die Hauptursache für die Komplexität immer noch der Mischvorgang ist, während ein erheblicher Teil der am Mischen beteiligten Daten in den folgenden Phasen verworfen wird. Tatsache ist, dass der beschriebene Ansatz für jeden Benutzer eine vollständige zweistufige Nachbarschaft erstellt, während der Ego-Teilgraph nur eine relativ kleine Teilmenge dieser Nachbarschaft ist, die nur interne Bögen enthält.
Wenn wir zum Beispiel durch die Verarbeitung von Bobs direkten Nachbarn - Harry und Frank - wussten, dass sie keine Freunde voneinander sind, konnten wir bereits im ersten Schritt solche externen Pfade herausfiltern. Um jedoch für alle Gary und Frenkov herauszufinden, ob sie Freunde sind, müssen Sie das Freundschaftsdiagramm an allen Rechenknoten in den Speicher ziehen oder während der Verarbeitung jedes Datensatzes Fernaufrufe tätigen, was je nach den Bedingungen der Aufgabe unmöglich ist.
Dennoch gibt es eine Lösung, wenn wir uns in einem kleinen Prozentsatz der Fälle erlauben, Fehler zu machen, wenn wir eine Freundschaft finden, in der sie tatsächlich nicht existiert. Es gibt eine ganze Familie probabilistischer Datenstrukturen , die es ermöglichen, den Speicherverbrauch während der Datenspeicherung um Größenordnungen zu reduzieren und gleichzeitig eine gewisse Fehlermenge zuzulassen. Die bekannteste Struktur dieser Art ist der Bloom-Filter , der seit vielen Jahren erfolgreich in Industriedatenbanken eingesetzt wird, um Fehler im "Long Tail" -Cache auszugleichen.
Die Hauptaufgabe des Bloom-Filters besteht darin, die Frage zu beantworten: "Ist dieses Element in den vielen zuvor gesehenen Elementen enthalten?" Wenn der Filter mit "Nein" antwortet, ist das Element wahrscheinlich nicht in der Menge enthalten, aber wenn er mit "Ja" antwortet, besteht eine geringe Wahrscheinlichkeit, dass das Element immer noch nicht vorhanden ist.
In unserem Fall ist das "Element" ein Benutzerpaar, und die "Menge" sind alle Kanten des Diagramms. Dann kann der Bloom-Filter erfolgreich angewendet werden, um die Größe des Shuffle zu reduzieren:

Nachdem wir den Bloom-Filter im Voraus mit Informationen über das Diagramm vorbereitet haben, können wir durch Harrys Freunde herausfinden, dass Bob und Ilona keine Freunde sind, was bedeutet, dass wir Bob keine Informationen über die Verbindung zwischen Gary und Ilona senden müssen. Die Informationen, dass Harry und Bob alleine Freunde sind, müssen jedoch noch gesendet werden, damit Bob seine Freundschaftsgrafik nach der Gruppierung vollständig wiederherstellen kann.
Shuffle entfernen
Nach dem Anwenden des Filters wird die gesendete Datenmenge um ca. 80% reduziert, und die Aufgabe wird in 1 Stunde mit einer moderaten Clusterlast abgeschlossen, sodass Sie andere Aufgaben parallel parallel ausführen können. In diesem Modus kann es bereits "in Betrieb genommen" und täglich in Betrieb genommen werden, es besteht jedoch noch Optimierungspotenzial.
So paradox es auch klingen mag, das Problem kann gelöst werden, ohne auf Shuffle zurückzugreifen, wenn Sie sich einen bestimmten Prozentsatz an Fehlern erlauben. Und der Bloom-Filter kann uns dabei helfen:

Wenn wir Bobs Freundesliste mit einem Filter durchsehen, stellen wir fest, dass Alice und Charlie mit ziemlicher Sicherheit Freunde sind. Wir können den entsprechenden Bogen sofort zu Bobs Ego-Untergraph hinzufügen. Der gesamte Vorgang dauert in diesem Fall weniger als 15 Minuten und erfordert keine Datenübertragung über das Netzwerk. Abhängig von den Filtereinstellungen kann jedoch in der Realität ein bestimmter Prozentsatz der Lichtbögen fehlen.
Die vom Filter hinzugefügten zusätzlichen Bögen führen bei einigen Aufgaben nicht zu erheblichen Verzerrungen: Wenn Sie beispielsweise Dreiecke zählen, können Sie das Ergebnis leicht korrigieren, und wenn Sie Attribute für Algorithmen für maschinelles Lernen vorbereiten, kann die ML-Anpassung selbst die nächste Anpassung lernen.
Bei einigen Aufgaben führen zusätzliche Bögen jedoch zu einer fatalen Verschlechterung der Qualität des Ergebnisses: Wenn Sie beispielsweise mit einem entfernten Ego (ohne die Oberseite des Benutzers) nach verbundenen Komponenten im Ego-Teilgraphen suchen, steigt die Wahrscheinlichkeit einer „Phantombrücke“ zwischen den Komponenten quadratisch in Bezug auf ihre Größe, was dazu führt dass wir fast überall eine große Komponente bekommen.
Es gibt auch einen Zwischenbereich, in dem der negative Effekt zusätzlicher Bögen experimentell bewertet werden muss: Beispielsweise können einige Community- Suchalgorithmen ein wenig Rauschen recht erfolgreich bewältigen und eine nahezu identische Community-Struktur zurückgeben.
Anstelle einer Schlussfolgerung
Ego-Benutzer-Subgraphen sind eine wichtige Informationsquelle, die in OK aktiv verwendet wird, um die Qualität von Empfehlungen zu verbessern, demografische Daten zu verfeinern und Spam zu bekämpfen. Ihre Berechnung ist jedoch mit einer Reihe von Schwierigkeiten verbunden.
In dem Artikel untersuchten wir die Entwicklung des Ansatzes zur Erstellung von Ego-Subgraphen für alle Benutzer eines sozialen Netzwerks und konnten die Arbeitszeit von den ersten 20 Stunden auf 1 Stunde und bei einem kleinen Prozentsatz von Fehlern auf 10 bis 15 Minuten verbessern.
Die drei „Säulen“, auf denen die endgültige Entscheidung basiert, sind:
- Verwendung der Graphsymmetrieeigenschaft und der Tomas-Schank- Algorithmen.
- Speichern Sie Ego-Subgraphen mithilfe einer spärlichen CSR-Matrix effizient.
- Verwenden Sie einen Bloom-Filter , um die Datenübertragung über das Netzwerk zu reduzieren.
Beispiele für die Entwicklung des Algorithmuscodes finden Sie im Zeppelin-Notizbuch .