Auf Habré gab es bereits viele Artikel, die sich mit schnellen Berechnungen der Trigonometrie befassten, wenn dies dringend erforderlich ist, aber ich möchte sie mit einer kleinen Anmerkung unter Bezugnahme auf die Schultrigonometrie ergänzen.
Manchmal gibt es möglicherweise keine Hardware-Implementierung der Trigonometrie, manchmal gibt es andere Gründe, Methoden zur Beschleunigung der Berechnung zu erfinden.
Mathe
Erinnern wir uns an einige einfache Formeln aus dem Schulkurs.
Beginnen wir mit den einfachen:
(1)
sin x = cos (90° - x)cos x = sin (90° - x)sin -x = -sin xcos -x = cos x- Im allgemeinen Fall ist
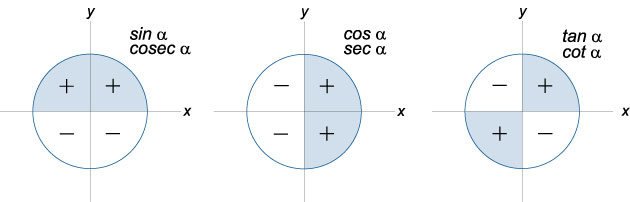
sin (90°N ± x) = ±cos x für ungerades N und ±sin x für gerade. Das Vorzeichen basiert auf dem Vorzeichen des Arguments im entsprechenden Viertel des Kreises.
Weiter:
(2)
cos (x + y) = cos x cos y - sin x sin ysin (x + y) = sin x cos y + cos x sin y
Und auch:
(3)
sin x = x - x^3/3! + x^5/5! - ...cos x = 1 - x^2/2! + x^4/4! - ...
Der Cosinus / Sinus eines beliebigen Winkels kann mit den Formeln der ersten Gruppe auf ein Argument im Bereich von 0 ° bis 45 ° reduziert werden.
Bei kleinen Winkeln können trigonometrische Funktionen auf asymptotische Erweiterungen reduziert werden, wenn die verworfenen Terme absichtlich über das Entladungsgitter hinausgehen.
Alle Zwischenwinkel können erhalten werden, indem große Winkel mit einem bestimmten Schritt summiert werden (und für sie kann die Trigonometrie als tabellarisch betrachtet werden), und Reste, die früher oder später eine lineare Zerlegung ergeben.
Anwendung
Angenommen, wir arbeiten mit IEEE-754-Zahlen mit einfacher Genauigkeit. Sie haben die Namen float, single usw. Die Mantisse enthält 23 Zeichen, was bedeutet, dass wir einen relativen Fehler von 2^-23 .
Lassen Sie uns bewerten, wie tief Sie gehen müssen, um Argumenttabellen zu erstellen.
Für den Sinus werden wir den kubischen Term verwerfen, daher muss seine Beziehung zum linearen Term kleiner sein als der zulässige Fehler, was bedeutet, dass: 1 - (x - x^3/3!) / x = x^2/6 2/6 2 ^ -23, woraus folgt, dass für Argumente von nicht mehr als 0,000846 Radiant die Genauigkeit der ungefähren Berechnung für den Sinus für uns ausreicht. Wenn Sie für den Kosinus den quadratischen Term fallen lassen, benötigen Sie eine Genauigkeit, die etwa zweimal besser ist - 0,000488 Bogenmaß.
Wir brauchen also keine Tabellenwerte für das Argument kleiner als 0,000488 Bogenmaß.
Um die Tabelle zu erstellen, normalisieren wir das Eingabeargument so, dass der Wert 0 einem Winkel von 0 ° und der Wert 1 einem Winkel von 45 ° entspricht oder pi/4=0.78539816 Bogenmaß. Dann wird der oben erhaltene Mindestwinkel in 0,0006217 Bogenmaß oder ungefähr 1/1600 umgerechnet - dies ist mehr als 1/2048 = 2^-11 .
Als nächstes müssen Sie den Schritt der Tabellen basierend darauf auswählen, wie wir die Berechnungen verteilen möchten. Wir werden den Exponenten 11 in mehrere Teile teilen. Sie können es beispielsweise in zwei Teile teilen: 11 = 6 + 5, dann benötigen wir zwei Tabellen mit den Einträgen 64 und 32 (insgesamt 96) oder drei Teile: 11 = 4 + 4 + 3 (die Größe der Tabellen beträgt 16 + 16 + 8) = 40 Einträge), aber es wird mehr Multiplikationsoperationen geben - die spezifische Auswahl hängt von der Aufgabe und den verfügbaren Ressourcen ab.
Hinweis: Ein Tabelleneintrag besteht aus zwei Sinus- und Cosinusargumenten. Bei einfacher Speicherung beträgt die Datensatzgröße 8 Byte.
Beispiel
Nehmen wir als Beispiel die Zerlegung 4 + 4 + 3 und verallgemeinern sie dann.
Also die Aufgabe: Berechne den Wert von sin x für ein beliebiges x .
Schritt 1. Wir bringen das Argument x auf unsere Skala und teilen es durch die Konstante pi/4 (nennen wir es x' ).
Schritt 2. Abhängig vom Wert des Arguments x' wählen wir mit den Formeln (1) die gewünschte Funktion so aus, dass ihr Argument im Bereich von 0 bis 1 (einschließlich) liegt (nennen wir x'' . In diesem Schritt müssen Sie auch das Vorzeichen des Ergebnisses markieren .
[Angenommen, der Sinus ist]
Schritt 3. Wir werden die Tabellen verwenden (ich möchte Sie daran erinnern, dass es 3 davon gibt), während die Indizes in der Tabelle "Bitfelder" in der binären Darstellung des Arguments x'' - die ersten 4 Bits nach dem Dezimalpunkt, dann 4 weitere und 3 weitere und die verbleibenden für das Geschäft Bits gehen zum Rest.
Der Tabellensinus heißt S1, S2, S3, die Tabellenkosinusse sind C1, C2, C3.
Da wir den Winkel durch pi/4 , muss er mit dem gleichen Betrag multipliziert werden, um den Rest im Bogenmaß zu erhalten. Der mit pi/4 multiplizierte "Bit" -Rest wird mit A bezeichnet. Dann ist sein Sinus gleich A und der Cosinus - 1.
Schritt 4. Kombinieren Sie alles, was passiert ist:
C12 = C1 C2 - S1 S2 S12 = S1 C2 + C1 S2 C123 = C12 C3 - S12 S2 S123 = S12 C3 + C12 S3
|sin x| = S123 + C123 A |sin x| = S123 + C123 A (wenn Sie in Schritt 2 einen Sinus erhalten haben)
|sin x| = C123 - S123 A |sin x| = C123 - S123 A (wenn Sie den Kosinus in Schritt 2 erhalten haben)
Schritt 5. Wenn wir in Schritt 2 der Ansicht waren, dass das Ergebnis negativ sein sollte, sollte dieses Minus in das Ergebnis eingegeben werden.
Fazit
Ein ähnlicher Ansatz kann sowohl zur Berechnung in reellen Zahlen beliebiger Größe als auch zum Implementieren einer speziellen Festkomma-Arithmetik verwendet werden. Eigentlich war es einmal nur die letzte Aufgabe, die mich dazu brachte, tiefer in diese Richtung zu graben, aber das ist lange her.