Wachstum. Gewicht. Drei Nachbarn

Auf der Suche nach einem interessanten und einfachen DataSet bin ich auf diesen gutaussehenden Mann gestoßen .

Über diese Schönheit

Es enthält Daten zu Wachstum und Gewicht von 10.000 Männern und Frauen . Keine Beschreibung. Nichts Überflüssiges". Nur Größe, Gewicht und Bodenmarkierung. Ich mochte diese mysteriöse Einfachheit.

Nun, fangen wir an!

Was war für mich interessant?

• Was ist der Gewichts- und Größenbereich für die meisten Männer und Frauen?
• Was für ein "durchschnittlicher" Mann und eine "durchschnittliche" Frau sind das?
• Kann das einfache KNN-Modell für maschinelles Lernen aus diesen Daten das Gewicht nach Größe vorhersagen ?

Lass uns gehen!

Erster Blick

Laden Sie zunächst die erforderlichen Module

#      import pandas as pd #     import matplotlib.pyplot as plt %matplotlib inline #    «  » from sklearn.neighbors import KNeighborsRegressor #         from sklearn.model_selection import train_test_split 

Wenn die Bibliotheken genau aufstanden, war es Zeit, das DataSet selbst zu laden und die ersten 10 Elemente zu betrachten. Dies ist notwendig, damit unser Darm ruhig ist, wir alles richtig geladen haben.

Seien Sie übrigens nicht beunruhigt, dass Größe und Gewicht sich von dem unterscheiden, was wir gewohnt sind. Dies liegt an einem anderen Messsystem: Zoll und Pfund anstelle von Zentimetern und Kilogramm .

 data = pd.read_csv('weight-height.csv') data.head(10) 

Gut! Wir sehen, dass die ersten zehn Einträge "Männer" sind. Wir sehen ihre Größe und ihr Gewicht . Daten gut geladen.

Jetzt können Sie die Anzahl der Zeilen im Satz anzeigen.

 data.shape >> (10000, 3) 

Zehntausend Zeilen / Datensätze. Und jeder hat drei Parameter . Was du brauchst!

Es ist Zeit, das Messsystem zu reparieren. Jetzt sind hier Zentimeter und Kilogramm.

 data['Height'] *= 2.54 data['Weight'] /= 2.205 #    data.head(10) 

Jetzt ist es vertrauter geworden. Und die allererste Aufzeichnung erzählt von einem Mann mit einer Größe von ~ 190 cm und einem Gewicht von ~ 110 kg. Großer Mann. Nennen wir ihn Bob.

Aber wie soll man verstehen: Ist es viel oder wenig im Vergleich zu den anderen? Ist es möglich, dass wir alle Plus- oder Minusbohnen sind? Das ist etwas später.

Lassen Sie uns nun herausfinden, wie symmetrisch die beiden Geschlechter in diesem Datensatz sind.

 data['Gender'].value_counts() >> Male 5000 Female 5000 Name: Gender, dtype: int64 

Idealerweise gleich verteilt. Und das ist gut so, denn wenn es 9999 Männer und 1 Frau gäbe, wäre es sinnlos, so zu tun, als würde dieses DataSet beide Geschlechter gleich gut offenbaren. In unserem Fall ist alles in Ordnung!

Teilen und lernen!

Die Intuition legt nahe, dass es richtig ist, die beiden Geschlechter zu trennen und getrennt zu erforschen. In der Tat sehen wir im Leben oft, dass Männer und Frauen plus oder minus unterschiedliche Größe und Gewicht haben

 #  data_male = data[data['Gender'] == 'Male'].copy() #  data_female = data[data['Gender'] == 'Female'].copy() 

Werfen wir einen Blick auf die kleinen beschreibenden Statistiken, die uns das Pandas- Modul bietet.

Männer :

 data_male.describe() 

Frauen :

 data_female.describe() 

Wir sehen, dass bei Männern der Durchschnitt und der Median 175 cm und 85 kg betragen. Und bei Frauen : 162 cm und 62 kg. Dies zeigt uns, dass es keine starken Emissionen gibt. Oder sie sind auf beiden Seiten des Medians symmetrisch. Welches ist sehr selten.

Beide Geschlechter weisen jedoch geringfügige Abweichungen des Mittelwerts vom Median auf. Aber sie sind unbedeutend und nur auf Hundertstel sichtbar. Lass uns weitermachen!

Histogramm

Dies ist ein Diagramm, das die Werte von Minimum bis Maximum in der Reihenfolge des Wachstums darstellt und die Anzahl der einzelnen Instanzen zeigt.

 fig, axes = plt.subplots(2,2, figsize=(20,10)) plt.subplots_adjust(wspace=0, hspace=0) axes[0,0].hist(data_male['Height'], label='Male Height', bins=100, color='red') axes[0,1].hist(data_male['Weight'], label='Male Weight', bins=100, color='red', alpha=0.4) axes[1,0].hist(data_female['Height'], label='Female Height', bins=100, color='blue') axes[1,1].hist(data_female['Weight'], label='Female Weight', bins=100, color='blue', alpha=0.4) axes[0,0].legend(loc=2, fontsize=20) axes[0,1].legend(loc=2, fontsize=20) axes[1,0].legend(loc=2, fontsize=20) axes[1,1].legend(loc=2, fontsize=20) plt.savefig('plt_histogram.png') plt.show() 

Die Daten werden glockenförmig verteilt. Sehr ähnlich zur Normalverteilung .

Zusätzlich zu statistischen Tests für die Normalverteilung gibt es einen visuellen Test. Wenn die Verteilung nach Typ und Logik normal zu sein scheint, können wir mit einigen Annahmen davon ausgehen, dass wir es damit zu tun haben.

Man könnte einen statistischen Normalitätstest durchführen und den p-Wert bestimmen, aber Ich kann nicht Dies würde den Rahmen des Artikels sprengen.

Lernen, mit Stiften zu arbeiten

Pandas können für uns viel zählen. Sie müssen jedoch mindestens einmal selbst einige Statistiken zählen. Jetzt werde ich zeigen, wie die Standardabweichung berechnet wird .

Lassen Sie es uns am Beispiel der Menschen und des charakteristischen Wachstums tun.

Durchschnitt

Formel

$$

$$M = \ frac {1} {N} \ sum \ limit_ {i = 1} ^ N n_i$$

wo

• M - Durchschnittswert
• N ist die Anzahl der Instanzen
• ni - einzelne Instanz

Code:

 mean = data_male['Height'].mean() print('mean:\t{:.2f}'.format(mean)) >> mean: 175.33 

Durchschnittliche Höhe - 175cm

Abweichung im Quadrat

$$

$$d_i = (n_i - M) ^ 2$$

wo

• di - einzelne Abweichung
• ni - einzelne Instanz
• M - Durchschnitt

Code:

 data_male['Height_d'] = (data_male['Height'] - mean) ** 2 data_male['Height_d'].head(10) >> 0 149.927893 1 0.385495 2 166.739089 3 47.193692 4 4.721246 5 20.288347 6 0.375539 7 2.964214 8 25.997623 9 200.149603 Name: Height_d, dtype: float64 

Dispersion

Formel

$$

$$D = \ frac {1} {N} \ sum \ limit_ {i = 1} ^ N d_i$$

wo

• D ist der Dispersionswert
• di - einzelne Abweichung
• N ist die Anzahl der Instanzen

Code:

 disp = data_male['Height_d'].mean() print('disp:\t{:.2f}'.format(disp)) >> disp: 52.89 

Dispersion - 53

Standardabweichung

Formel

$$

$$std = \ sqrt {D}$$

wo

• Standard - Standardabweichungswert
• D ist der Dispersionswert

Code:

 std = disp ** 0.5 print('std:\t{:.2f}'.format(std)) >> std: 7.27 

Standardabweichung - 7

Konfidenzintervalle

Jetzt werden wir herausfinden, in welchen Wachstums- und Gewichtsbereichen 68%, 95% und 99,7% der Männer und Frauen liegen .

Dies ist nicht so schwierig - Sie müssen die Standardabweichung vom Durchschnitt addieren und subtrahieren . Es sieht so aus:

• 68% - plus oder minus eine Standardabweichung
• 95% - plus oder minus zwei Standardabweichungen
• 99,7% - plus oder minus drei Standardabweichungen

Wir schreiben eine Hilfsfunktion, die dies berücksichtigt:

 def get_stats(series, title='noname'): #    print('= {} =\n'.format(title.upper())) #     pandas descr = series.describe() #   mean = descr['mean'] print('= Mean:\t{:.0f}'.format(mean)) #    std = descr['std'] print('= Std:\t{:.0f}'.format(std)) #    print('\n= = = =\n') #   ## 68% devi_1 = [mean - std, mean + std] ## 95% devi_2 = [mean - 2 * std, mean + 2 * std] ## 99.7% devi_3 = [mean - 3 * std, mean + 3 * std] #   print('= 68% is from\t\t{:.0f} to {:.0f}'.format(devi_1[0], devi_1[1])) print('= 95% is from\t\t{:.0f} to {:.0f}'.format(devi_2[0], devi_2[1])) print('= 99.7% is from\t\t{:.0f} to {:.0f}'.format(devi_3[0], devi_3[1])) 

Nun, wenden Sie es auf die Daten an:

Männer | Wachstum

 get_stats(data_male['Height'], title='Male Height') >> = MALE HEIGHT = = Mean: 175 = Std: 7 = = = = = 68% is from 168 to 183 = 95% is from 161 to 190 = 99.7% is from 154 to 197 

Männer | Gewicht

 get_stats(data_male['Height'], title='Male Height') >> = MALE WEIGHT = = Mean: 85 = Std: 9 = = = = = 68% is from 76 to 94 = 95% is from 67 to 103 = 99.7% is from 58 to 112 

Frauen | Wachstum

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE HEIGHT = = Mean: 162 = Std: 7 = = = = = 68% is from 155 to 169 = 95% is from 148 to 176 = 99.7% is from 141 to 182 

Frauen | Gewicht

 get_stats(data_male['Height'], title='Male Height') >> = FEMALE WEIGHT = = Mean: 62 = Std: 9 = = = = = 68% is from 53 to 70 = 95% is from 44 to 79 = 99.7% is from 36 to 87 

Daher die Schlussfolgerungen:

• Die meisten Männer: 154 cm - 197 cm und 58 kg - 112 kg.
• Die meisten Frauen: 141 cm - 182 cm und 36 kg - 87 kg.

Jetzt müssen Sie nur noch maschinelles Lernen auf dieses Set anwenden und versuchen, das Gewicht anhand der Größe vorherzusagen.

Nächste Nachbarn

Der Algorithmus "Zu den nächsten Nachbarn" ist einfach. Es existiert für Klassifizierungsaufgaben - um eine Katze von einem Hund zu unterscheiden - und für Regressionsaufgaben - um das Gewicht nach Größe zu erraten. Das brauchen wir!

Für die Regression verwendet er den folgenden Algorithmus:

• Erinnert sich an alle Datenpunkte
• Wenn ein neuer Punkt angezeigt wird, sucht er nach K seinen nächsten Nachbarn (die Nummer K wird vom Benutzer festgelegt).
• Mittelung des Ergebnisses
• Gibt eine Antwort

Zuerst müssen Sie den Datensatz in die Trainings- und Testteile aufteilen und den Algorithmus testen

An Männern experimentieren

 X_train, X_test, y_train, y_test = train_test_split(data_male['Height'], data_male['Weight']) 

Geteilt ist es Zeit, es zu versuchen.

 #   knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8298400793623182 #   knr5 = KNeighborsRegressor(n_neighbors=5) knr5.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr5.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7958051642678619 #   knr7 = KNeighborsRegressor(n_neighbors=7) knr7.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr7.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.7769249318420969 

Wir werden nicht weit gehen und bei drei Nachbarn anhalten. Aber die Frage ist: Kann ein solches Modell mein Gewicht erraten?

 knr3.predict([[180]])[0, 0] >> 88.67596236265881 

88kg ist sehr nah. In dieser Sekunde wiege ich 89,8 kg

Vorhersagekarte für Männer

Die Zeit, um meinen Lieblingsteil der Wissenschaft aufzubauen, ist Grafik.

 array_male = [] #   99.7% xaxis = range(154, 198) for h in xaxis: ans = knr3.predict([[h]]) array_male.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male, 'r-', linewidth=4) plt.title('Male heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_male.png') plt.show() 

Modell- und Vorhersagekarte für Frauen

 X_train, X_test, y_train, y_test = train_test_split(data_female['Height'], data_female['Weight']) knr3 = KNeighborsRegressor(n_neighbors=3) knr3.fit(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) knr3.score(X_train.values.reshape(-1,1), y_train.values.reshape(-1,1)) >> 0.8135681584074799 

 array_female = [] #   99.7% xaxis = range(141, 183) for h in xaxis: ans = knr3.predict([[h]]) array_female.append(ans[0, 0]) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_female, 'b-', linewidth=4) plt.title('Female heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_female.png') plt.show() 

Und natürlich ist es interessant, wie diese Grafiken zusammen aussehen:

 #      xaxis = range(154, 183) plt.figure(figsize=(20,10)) plt.plot(xaxis, array_male[:-15], 'r-', linewidth=4) plt.plot(xaxis, array_female[13:], 'b-', linewidth=4) plt.title('Together heght-weight dependence', fontsize=30) plt.xlabel('Height', fontsize=30) plt.ylabel('Weight', fontsize=30) plt.grid() plt.savefig('plt_knn_together.png') plt.show() 

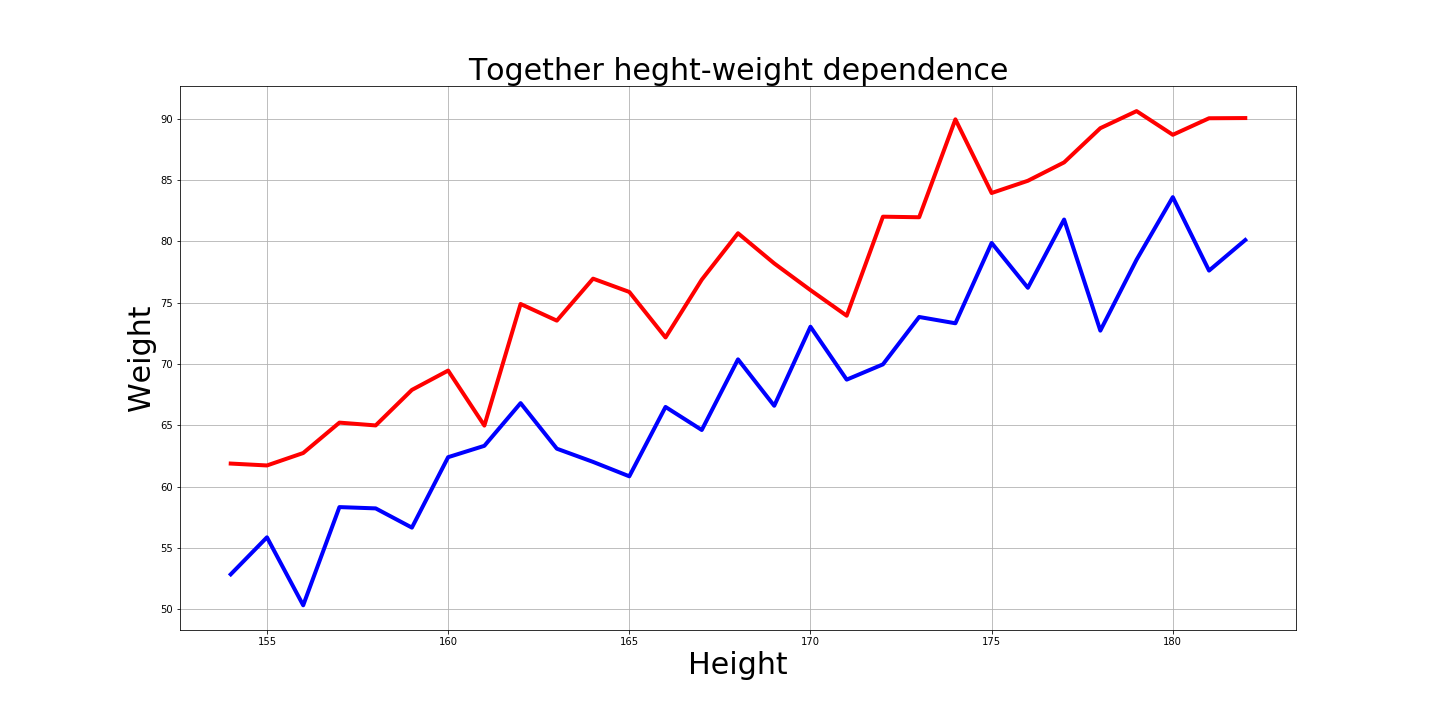
Antworten auf Fragen

- Wie groß ist das Gewicht und die Größe der meisten Männer und Frauen?

99,7% der Männer: von 154 cm bis 197 cm und von 58 kg bis 112 kg.
Und 99,7% der Frauen: von 141 cm bis 182 cm und von 36 kg bis 87 kg.

- Was für ein "durchschnittlicher" Mann und eine "durchschnittliche" Frau sind das?

Der durchschnittliche Mann ist 175 cm und 85 kg.
Und die durchschnittliche Frau ist 162 cm und 62 kg.

- Wird das einfache maschinelle KNN-Lernmodell aus diesen Daten das Gewicht nach Größe vorhersagen?

Ja, das Modell hat 88 kg vorhergesagt, und ich habe 89,8 kg.

Alles, was ich getan habe, habe ich hier gesammelt

Nachteile des Artikels

• Es gibt keine Beschreibung von DataSet. Wahrscheinlich waren Alter und andere Faktoren bei Menschen unterschiedlich. Daher kann man es nicht im Glauben akzeptieren, sondern zum Experimentieren - bitte.
• Auf eine gute Weise - es war notwendig, einen Test auf Normalverteilung zu machen

Nachwort

Zum Beispiel, wenn Sie das 99,7% -Intervall erreichen