ClickHouse stößt ständig auf Zeichenfolgenverarbeitungsaufgaben. Zum Beispiel das Suchen, Berechnen der Eigenschaften von UTF-8-Zeichenfolgen oder etwas Exotischeres, unabhängig davon, ob es sich um eine Suche mit Groß- und Kleinschreibung oder eine Suche mit komprimierten Daten handelt.
Angefangen hat alles damit, dass die ClickHouse-Entwicklungsleiterin Lyosha Milovidov o6CuFl2Q an der Fakultät für Informatik der Higher School of Economics zu uns kam und eine Vielzahl von Themen für Hausarbeiten und Diplome anbot. Als ich „Smart String Processing Algorithms in ClickHouse“ sah (ich, eine Person, die sich für verschiedene Algorithmen interessiert, einschließlich experimenteller), habe ich sofort Pläne aufgestellt, wie man das coolste Diplom macht. Meine Freude und mein Ausdruck können wie folgt beschrieben werden:

Clickhouse
ClickHouse hat die Organisation der Datenspeicherung im Speicher sorgfältig durchdacht - in Spalten. Am Ende jeder Spalte befindet sich ein Abstand von 15 Bytes zum sicheren Lesen eines 16-Byte-Registers. Beispielsweise speichert ColumnString nullterminierte Zeichenfolgen zusammen mit Offsets. Es ist sehr bequem, mit solchen Arrays zu arbeiten.

Es gibt auch ColumnFixedString, ColumnConst und LowCardinality, aber wir werden heute nicht so ausführlich darüber sprechen. Der Hauptpunkt an dieser Stelle ist, dass das Design des sicheren Lesens der Schwänze in Ordnung ist und die Lokalität der Daten auch bei der Verarbeitung eine Rolle spielt.
Teilstring-Suche
Höchstwahrscheinlich kennen Sie viele verschiedene Algorithmen zum Finden eines Teilstrings in einem String. Wir werden über diejenigen sprechen, die in ClickHouse verwendet werden. Zuerst stellen wir einige Definitionen vor:
- Heuhaufen - die Linie, in die wir schauen; typischerweise wird die Länge mit n bezeichnet .
- Nadel - die Zeichenfolge oder der reguläre Ausdruck, nach dem wir suchen; Die Länge wird mit m bezeichnet .
Nachdem ich eine große Anzahl von Algorithmen studiert habe, kann ich sagen, dass es 2 (maximal 3) Arten von Teilstring-Suchalgorithmen gibt. Das erste ist die Erstellung von Suffixstrukturen in der einen oder anderen Form. Der zweite Typ sind Algorithmen, die auf einem Speichervergleich basieren. Es gibt auch den Rabin-Karp-Algorithmus, der Hashes verwendet, aber in seiner Art ziemlich einzigartig ist. Der schnellste Algorithmus existiert nicht, alles hängt von der Größe des Alphabets, der Länge der Nadel, dem Heuhaufen und der Häufigkeit des Auftretens ab.
Lesen Sie hier mehr über verschiedene Algorithmen. Und hier sind die beliebtesten Algorithmen:
- Knut - Morris - Pratt,
- Boyer - Moore,
- Boyer - Moore - Horspool,
- Rabin - Karpfen,
- Doppelseitig (wird in glibc als "memmem" bezeichnet),
- BNDM
Die Liste geht weiter. Wir bei ClickHouse haben ehrlich alles versucht, aber am Ende haben wir uns für eine außergewöhnlichere Version entschieden.
Volnitsky-Algorithmus
Der Algorithmus wurde Ende 2010 im Blog des Programmierers Leonid Volnitsky veröffentlicht. Es ähnelt etwas dem Boyer-Moore-Horspool-Algorithmus, nur eine verbesserte Version.
Wenn m <4 ist , wird der Standardsuchalgorithmus verwendet. Speichern Sie alle Bigrams-Nadeln (2 aufeinanderfolgende Bytes) vom Ende in einer Hash-Tabelle mit offener Adressierung der Größe | Sigma | 2 Elemente (in der Praxis sind dies 2 16 Elemente), wobei die Offsets dieses Bigrams die Werte und das Bigram selbst gleichzeitig der Hash und der Index sind. Die Ausgangsposition befindet sich ab Beginn des Heuhaufens auf Position m - 2 . Wir folgen dem Heuhaufen mit Schritt m - 1 , betrachten das nächste Bigram von dieser Position im Heuhaufen und betrachten alle Werte des Bigrams in der Hash-Tabelle. Dann werden wir zwei Speicherstücke mit dem üblichen Vergleichsalgorithmus vergleichen. Der verbleibende Schwanz wird von demselben Algorithmus verarbeitet.
Schritt m - 1 wird so gewählt, dass bei Auftreten einer Nadel im Heuhaufen das Bigram dieses Eintrags definitiv berücksichtigt wird, wodurch sichergestellt wird, dass die Position des Eintrags im Heuhaufen zurückgegeben wird. Das erste Auftreten wird durch die Tatsache garantiert, dass wir der Hash-Tabelle per Bigram Indizes vom Ende hinzufügen. Dies bedeutet, dass wir, wenn wir von links nach rechts gehen, zuerst die Bigramme vom Ende der Zeile betrachten (vielleicht zunächst völlig unnötige Bigramme), dann näher am Anfang.
Betrachten Sie ein Beispiel. Lassen Sie den Heuhaufen abacabaac und Nadel gleich aaca . Die Hash-Tabelle lautet {aa : 0, ac : 1, ca : 2} .
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
Wir sehen das Bigram ac . In Nadel ist es, wir ersetzen in Gleichheit:
0 1 2 3 4 5 6 7 8 9 abacabaaca aaca
Nicht übereinstimmend. Nachdem ac keine Einträge in der Hash-Tabelle enthält, fahren wir mit Schritt 3 fort:
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
Es gibt keine Bigrams in der Hash-Tabelle.
0 1 2 3 4 5 6 7 8 9 abacabaaca ^ -
Es gibt ein Bigram ca in der Nadel, wir schauen uns den Versatz an und finden den Eintrag:
0 1 2 3 4 5 6 7 8 9 abacabaaca aaca
Der Algorithmus hat viele Vorteile. Erstens müssen Sie keinen Speicher auf dem Heap zuweisen, und 64 KB auf dem Stapel sind jetzt nicht mehr transzendent. Zweitens ist 2 16 eine ausgezeichnete Zahl, um Modulo für den Prozessor zu nehmen; Dies sind nur Movzwl-Anweisungen (oder, wie wir scherzen, „Movsvl“) und die Familie.
Im Durchschnitt erwies sich dieser Algorithmus als der beste. Wir haben die Daten von Yandex.Metrica übernommen, die Anfragen sind fast real. Eine Stream-Geschwindigkeit, mehr ist besser, KMP: Knut-Morris-Pratt-Algorithmus, BM: Boyer-Moore, BMH: Boyer-Moore-Horspool.
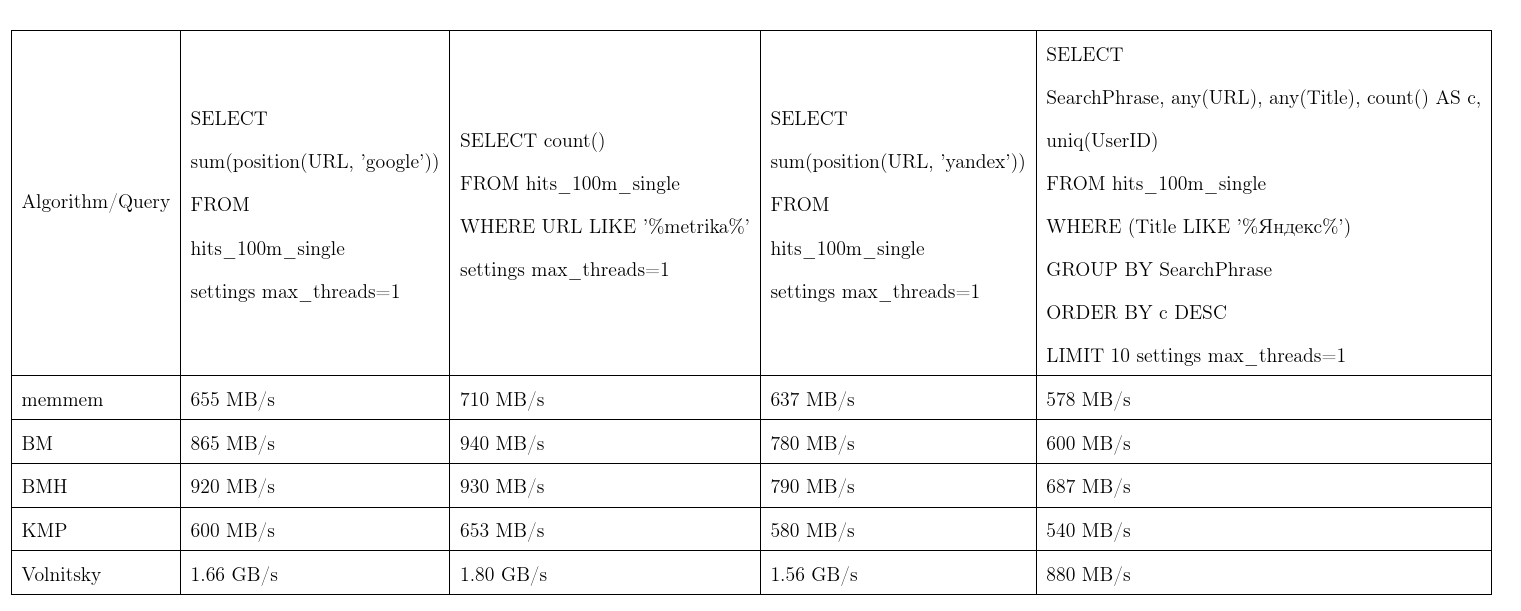
Um nicht unbegründet zu sein, kann der Algorithmus quadratische Zeit arbeiten:

Es wird in der position(Column, ConstNeedle) und dient auch als Optimierung für die Suche nach regulären Ausdrücken.
Suche nach regulären Ausdrücken
Wir zeigen Ihnen, wie ClickHouse die Suche nach regulären Ausdrücken optimiert. Viele reguläre Ausdrücke enthalten einen Teilstring, der sich im Heuhaufen befinden muss. Um keine Finite-State-Maschine zu erstellen und dagegen zu prüfen, werden wir solche Teilzeichenfolgen isolieren.
Dies zu tun ist ganz einfach: Alle öffnenden Klammern erhöhen den Verschachtelungsgrad, alle schließenden Klammern verringern sich; Es gibt auch Zeichen, die für reguläre Ausdrücke spezifisch sind (z. B. '.', '*', '?', '\ w' usw.). Wir müssen alle Teilzeichenfolgen auf Stufe 0 bringen. Betrachten Sie ein Beispiel:
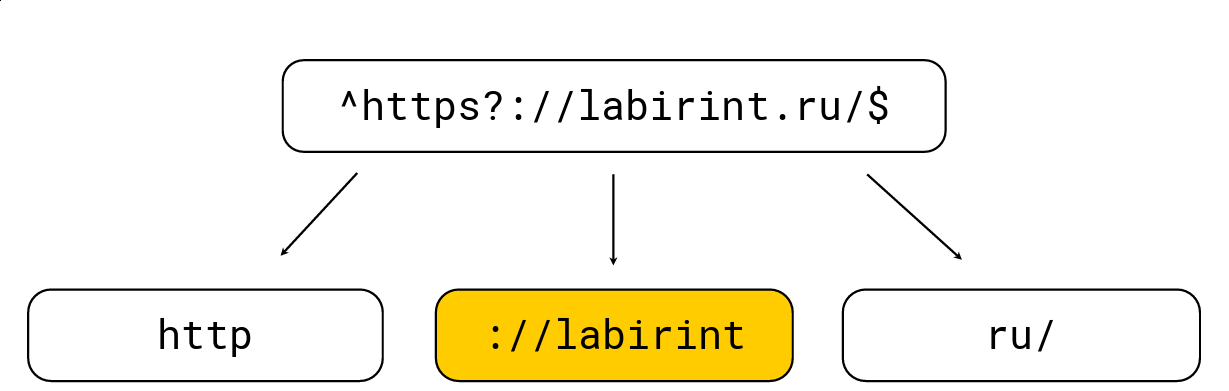
Wir teilen es in die Teilzeichenfolgen auf, die sich aus dem regulären Ausdruck im Heuhaufen befinden müssen. Danach wählen wir die maximale Länge aus, suchen nach Kandidaten und überprüfen dies mit der üblichen regulären Ausdrucks-Engine RE2. Im obigen Bild gibt es einen regulären Ausdruck, der von der üblichen RE2-Engine mit 736 MB / s verarbeitet wird, Hyperscan (etwas später) erreicht 1,6 GB / s und wir verwalten 1,69 GB / s pro Kern zusammen mit der Dekomprimierung LZ4. Im Allgemeinen ist eine solche Optimierung an der Oberfläche und beschleunigt die Suche nach regulären Ausdrücken erheblich, wird jedoch häufig nicht in Tools implementiert, was mich sehr überrascht.
Das Schlüsselwort LIKE wird ebenfalls mit diesem Algorithmus optimiert. Erst nach LIKE kann ein sehr vereinfachter regulärer Ausdruck %%%%% (beliebige Teilzeichenfolge) und _ (beliebiges Zeichen) durchlaufen.
Leider unterliegen nicht alle regulären Ausdrücke solchen Optimierungen. Beispielsweise ist es bei yandex|google unmöglich, yandex|google , die im Heuhaufen vorkommen müssen, explizit zu extrahieren. Deshalb haben wir eine völlig andere Lösung gefunden.
Suchen Sie nach vielen Teilzeichenfolgen
Das Problem ist, dass es viel Nadel gibt, und ich möchte verstehen, ob mindestens eine davon im Heuhaufen enthalten ist. Es gibt ziemlich klassische Methoden für eine solche Suche, zum Beispiel den Aho-Korasik-Algorithmus. Aber er war nicht zu schnell für unsere Aufgabe. Wir werden etwas später darüber sprechen.
Lesha ClickHouse liebt nicht standardisierte Lösungen, daher haben wir uns entschlossen, etwas anderes auszuprobieren und möglicherweise selbst einen neuen Suchalgorithmus zu entwickeln. Und sie taten es.
Wir haben uns den Volnitsky-Algorithmus angesehen und ihn so modifiziert, dass er nach vielen Teilzeichenfolgen gleichzeitig sucht. Dazu müssen Sie nur die Bigrams aller Zeilen hinzufügen und den Zeilenindex in der Hash-Tabelle speichern. Der Schritt wird aus mindestens allen Nadellängen minus 1 ausgewählt, um erneut die Eigenschaft zu gewährleisten, dass bei einem Auftreten das Bigram angezeigt wird. Die Hash-Tabelle wächst auf 128 KB (Zeilen, die länger als 255 sind, werden vom Standardalgorithmus verarbeitet, wir werden nicht mehr als 256 Nadeln berücksichtigen). Ich bin sehr faul, daher hier ein Beispiel aus der Präsentation (von links nach rechts von oben nach unten gelesen):


Wir begannen zu untersuchen, wie sich ein solcher Algorithmus im Vergleich zu anderen verhält (Zeilen werden aus realen Daten entnommen). Und für eine kleine Anzahl von Zeilen macht er alles (die Geschwindigkeit zusammen mit dem Entladen wird angezeigt - ungefähr 2,5 GB / s).
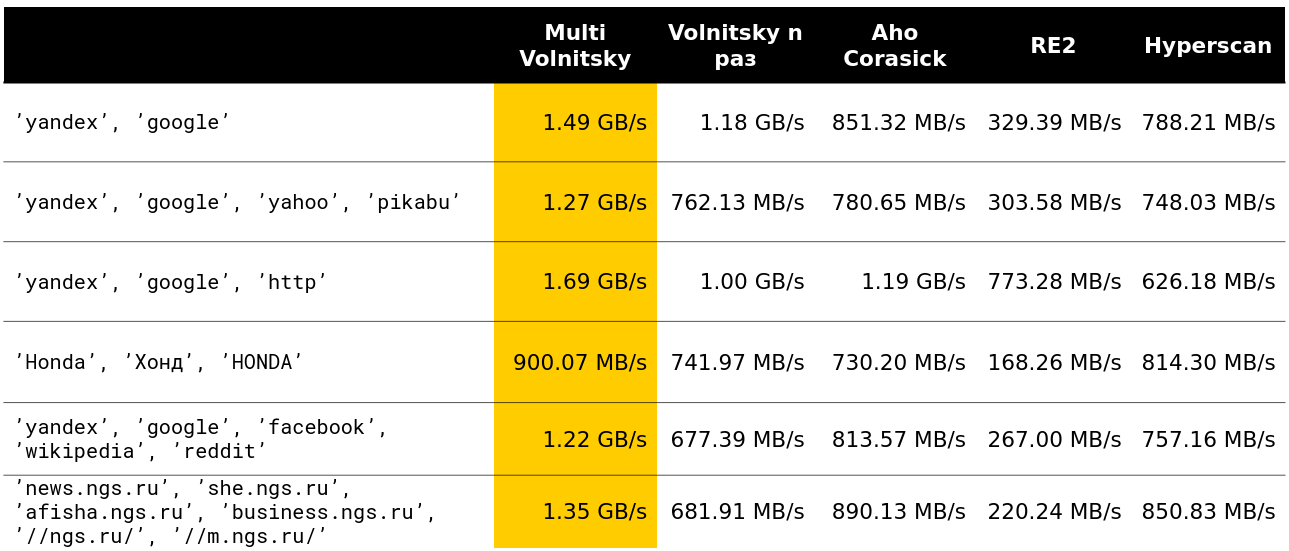
Dann wurde es interessant. Zum Beispiel verlieren wir mit einer großen Anzahl ähnlicher Bigrams gegen einige Konkurrenten. Es ist verständlich - wir beginnen, viele Erinnerungsstücke zu vergleichen und zu verschlechtern.

Sie können nicht viel beschleunigen, wenn die Mindestlänge der Nadel groß genug ist. Offensichtlich haben wir mehr Möglichkeiten, ganze Heuhaufenstücke zu überspringen, ohne etwas dafür zu bezahlen.

Der Kipppunkt beginnt irgendwo in den Zeilen 13-15. Ungefähr 97% der Anfragen, die ich im Cluster gesehen habe, waren weniger als 15 Zeilen:
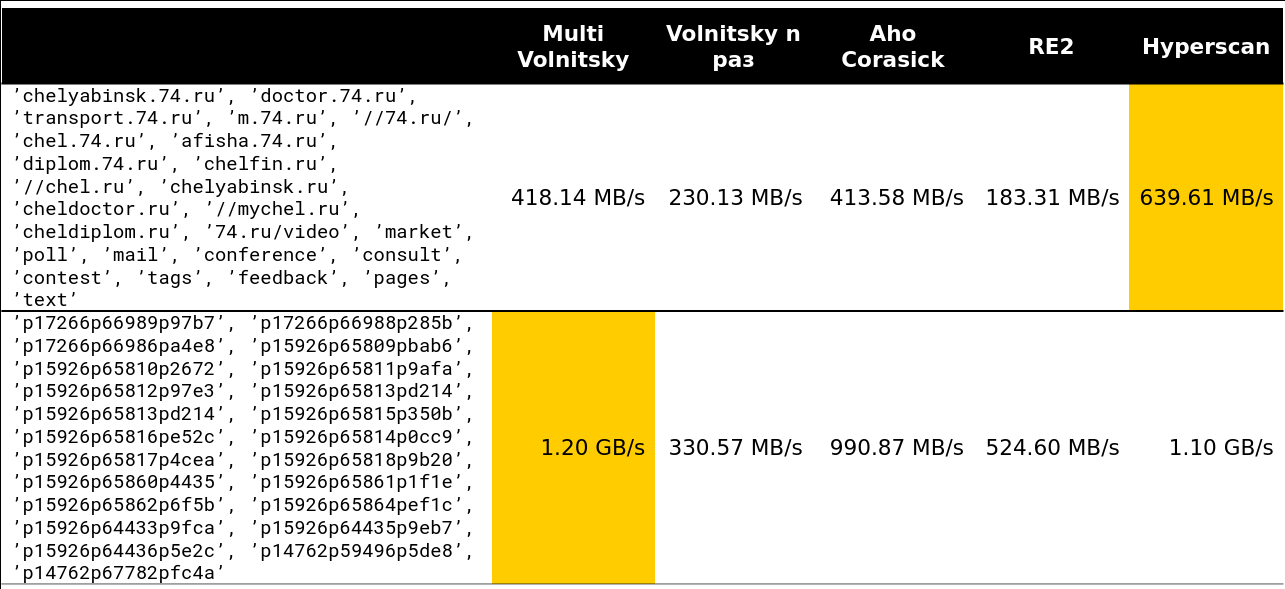
Nun, ein sehr beängstigendes Bild - 41 Zeilen, viele sich wiederholende Bigramme:

Infolgedessen haben wir in ClickHouse (19.5) die folgenden Funktionen durch diesen Algorithmus implementiert:
- multiSearchAny(h, [n_1, ..., n_k]) - 1, wenn sich mindestens eine der Nadeln im Heuhaufen befindet.
- multiSearchFirstPosition(h, [n_1, ..., n_k]) - die Position ganz links beim Eintritt in den Heuhaufen (von eins) oder 0, wenn nicht gefunden.
- multiSearchFirstIndex(h, [n_1, ..., n_k]) - der Nadelindex ganz links, der im Heuhaufen gefunden wurde; 0 wenn nicht gefunden.
- multiSearchAllPositions(h, [n_1, ..., n_k]) - Alle ersten Positionen aller Nadeln geben ein Array zurück.
Die Suffixe sind -UTF8 (wir normalisieren nicht), -CaseInsensitive (fügen Sie 4 Bigrams mit unterschiedlicher Groß- / Kleinschreibung hinzu), -CaseInsensitiveUTF8 (es gibt eine Bedingung, dass Groß- und Kleinbuchstaben die gleiche Anzahl von Bytes haben müssen). Siehe die Implementierung hier .
Danach fragten wir uns, ob wir mit vielen regulären Ausdrücken etwas Ähnliches machen könnten. Und sie fanden eine Lösung, die bereits in Benchmarks verwöhnt war.
Suche nach vielen regulären Ausdrücken
Hyperscan ist eine Bibliothek von Intel, die sofort nach vielen regulären Ausdrücken sucht. Es verwendet Heuristiken, um Unterwörter von regulären Ausdrücken zu isolieren, über die wir geschrieben haben, und viele SIMDs, um nach dem Glushkov-Automaten zu suchen (der Algorithmus scheint Teddy zu heißen).
Im Allgemeinen steht alles in der besten Tradition, das Maximum aus der Suche nach regulären Ausdrücken herauszuholen. Die Bibliothek macht wirklich das, was in ihren Funktionen deklariert ist.

Glücklicherweise konnte ich in meinem Entwicklungsmonat bei ClickHouse die 12-jährige Entwicklung einer anständigen Klasse von Abfragen überholen, und ich bin sehr zufrieden damit.
In Yandex wird die Hyperscan-Bibliothek auch in Antispam verwendet. Den Bewertungen nach zu urteilen, verarbeitet sie ruhig Tausende von regulären Ausdrücken und sucht schnell nach ihnen.
Die Bibliothek hat mehrere Nachteile. Die erste ist die nicht dokumentierte Menge an verbrauchtem Speicher und eine seltsame Eigenschaft, dass der Heuhaufen weniger als 2 32 Bytes betragen muss. Das zweite - Sie können die ersten Positionen nicht kostenlos zurückgeben, die Nadelindizes ganz links usw. Und das dritte Minus - es gibt einige Fehler aus heiterem Himmel. Daher haben wir bei ClickHouse die folgenden Funktionen mit Hyperscan implementiert:
- multiMatchAny(h, [n_1, ..., n_k]) - 1, wenn mindestens eine der Nadeln einen Heuhaufen gefunden hat.
- multiMatchAnyIndex(h, [n_1, ..., n_k]) - Jeder Index der Nadel, der multiMatchAnyIndex(h, [n_1, ..., n_k]) Heuhaufen multiMatchAnyIndex(h, [n_1, ..., n_k]) .
Wir sind interessiert, aber wie können Sie nicht genau, sondern ungefähr suchen? Und kam mit mehreren Lösungen.
Ungefähre Suche
Der Standard bei der ungefähren Suche ist der Levenshtein-Abstand - die Mindestanzahl von Zeichen, die ersetzt, hinzugefügt und entfernt werden können, um eine Zeichenfolge b der Länge n aus einer Zeichenfolge a der Länge m zu erhalten. Leider funktioniert der naive dynamische Programmieralgorithmus für O (mn) ; Die besten Köpfe von ShAD können dies in O (mn / log max (n, m)) tun. man kann sich leicht O ((n + m) ⋅ alpha) vorstellen , wobei alpha die Antwort ist; Die Wissenschaft kann dies für O ((alpha - | n - m |) min (m, n, alpha) + m + n) (der Algorithmus ist einfach, zumindest im ShAD lesen) oder, wenn etwas klarer, für O (alpha ^ 2 + m ) tun + n) . Es gibt immer noch ein Minus: Es ist höchstwahrscheinlich unmöglich, die quadratische Zeit im schlimmsten Fall polynomiell loszuwerden - Peter Indik hat einen sehr mächtigen Artikel darüber geschrieben.
Es gibt eine Übung: Stellen Sie sich vor, Sie zahlen für das Ersetzen eines Charakters in der Levenshtein-Distanz eine Geldstrafe von nicht zwei, sondern zwei; Überlegen Sie sich dann einen Algorithmus für O ((n + m) log (n + m)) .
Es funktioniert immer noch nicht, zu lang und zu teuer. Mit Hilfe dieser Entfernung haben wir jedoch Tippfehler in den Abfragen erkannt.
Neben der Levenshtein-Distanz gibt es eine Hamming-Distanz. Auch bei ihm ist alles ziemlich schlecht, aber ein bisschen besser als bei der Levenshtein-Distanz. Das Entfernen von Zeichen wird nicht berücksichtigt, sondern nur für zwei Zeilen gleicher Länge die Anzahl der Zeichen berücksichtigt, in denen sie sich unterscheiden. Wenn wir also den Abstand für Zeichenfolgen mit der Länge m <n verwenden, dann nur bei der Suche nach den nächsten Teilzeichenfolgen.
Wie berechnet man ein solches Array von Diskrepanzen (ein Array d von n - m + 1 Elementen, wobei d [i] die Anzahl der verschiedenen Zeichen im i-ten vom Beginn der Überlagerung ist) für O (| Sigma | (n + m) log (n + m) ) ? Machen Sie zuerst | Sigma | Bitmasken, die angeben, ob dieses Symbol dem betrachteten entspricht. Als nächstes berechnen wir die Antwort für jede der Sigma-Masken und fügen hinzu - wir erhalten die ursprüngliche Antwort.
Betrachten Sie ein Beispiel. abba , Teilzeichenfolge ba , binäres Alphabet. Wir erhalten 2 Masken 1001, 01 und 0110, 10 .
a 1001 01 - 0 01 - 0 01 - 1
b 0110 10 - 0 10 - 1 10 - 1
Wir bekommen das Array [0, 1, 2] - das ist fast die richtige Antwort. Beachten Sie jedoch, dass für jeden Buchstaben die Anzahl der Übereinstimmungen nur das Skalarprodukt einer festen Binärnadel und aller Heuhaufen-Teilzeichenfolgen ist. Und dafür gibt es natürlich eine schnelle Fourier-Transformation!
Für diejenigen, die es nicht wissen: Die FFT kann zwei Polynome von Grad m <n in einer Zeit O (n log n) multiplizieren, vorausgesetzt, die Arbeit mit den Koeffizienten wird pro Zeiteinheit durchgeführt. Faltungen sind skalaren Produkten sehr ähnlich. Es reicht aus, die Koeffizienten des ersten Polynoms zu duplizieren und das zweite zu erweitern und mit der erforderlichen Anzahl von Nullen zu ergänzen. Dann erhalten wir alle Skalarprodukte einer Binärzeichenfolge und alle Teilzeichenfolgen der anderen in O (n log n) - eine Art Magie! Aber glauben Sie mir, das ist absolut real, und manchmal tun es die Leute.
Aber nicht in ClickHouse. Für uns arbeiten wir mit | Sigma | = 30 ist bereits groß, und die FFT ist nicht der angenehmste praktische Algorithmus für den Prozessor oder, wie sie bei gewöhnlichen Menschen sagen, "die Konstante ist groß".
Aus diesem Grund haben wir uns für andere Metriken entschieden. Wir sind zur Bioinformatik gekommen, wo die Leute den n-Gramm-Abstand verwenden. Tatsächlich nehmen wir alle n-Gramm Heuhaufen und Nadel, betrachten 2 Multisets mit diesen n-Gramm. Dann nehmen wir die symmetrische Differenz und dividieren durch die Summe der Kardinalitäten zweier Multisets mit n-Gramm. Wir erhalten eine Zahl von 0 bis 1 - je näher an 0, desto ähnlicher sind die Linien. Betrachten Sie ein Beispiel mit n = 4 :
abcda → {abcd, bcda}; Size = 2 bcdab → {bcda, cdab}; Size = 2 . |{abcd, cdab}| / (2 + 2) = 0.5
Infolgedessen haben wir einen Abstand von 4 Gramm festgelegt und eine Reihe von Ideen von SSE dort festgehalten. Außerdem haben wir die Implementierung für Doppelbyte-crc32-Hashes leicht geschwächt.
Überprüfen Sie die Implementierung . Achtung: Sehr überzeugender und optimierter Code für Compiler.
Ich rate Ihnen besonders, auf den schmutzigen Hack zu achten, um Kleinbuchstaben für ASCII- und russische Codepunkte zu setzen.
- ngramDistance(haystack, needle) - gibt eine Zahl von 0 bis 1 zurück; Je näher an 0, desto mehr Linien sind einander ähnlich.
- -UTF8, -CaseInsensitive, -CaseInsensitiveUTF8 (Dirty Hack für Russen und ASCII).
Hyperscan steht auch nicht still - es verfügt über Funktionen für die ungefähre Suche: Sie können nach Linien suchen, die wie reguläre Ausdrücke aussehen, indem Sie Levenshteins konstanten Abstand angeben. Es wird ein Abstand + 1- Automat erstellt, der durch Löschen, Ersetzen oder Einfügen eines Zeichens, was „gut“ bedeutet, miteinander verbunden wird. Anschließend wird der übliche Algorithmus zum Überprüfen, ob ein Automat eine bestimmte Zeile akzeptiert, angewendet. In ClickHouse haben wir sie unter folgenden Namen implementiert:
- multiFuzzyMatchAny(haystack, distance, [n_1, ..., n_k]) - ähnlich wie multiMatchAny, nur mit Entfernung.
- multiFuzzyMatchAnyIndex(haystack, distance, [n_1, ..., n_k]) - ähnlich wie multiMatchAnyIndex, nur mit Entfernung.
Mit zunehmender Entfernung beginnt sich die Geschwindigkeit stark zu verschlechtern, bleibt aber immer noch auf einem recht anständigen Niveau.
Beenden Sie die Suche und beginnen Sie mit der Verarbeitung von UTF-8-Zeichenfolgen. Es gab auch viele interessante Dinge.
UTF-8-Zeilenverarbeitung
Ich gebe zu, dass es schwierig war, die Obergrenze für naive Implementierungen in UTF-8-codierten Zeichenfolgen zu durchbrechen. Es war besonders schwierig, SIMD zu schrauben. Ich werde einige Ideen dazu teilen.
Erinnern Sie sich daran, wie eine gültige UTF-8-Sequenz aussieht:
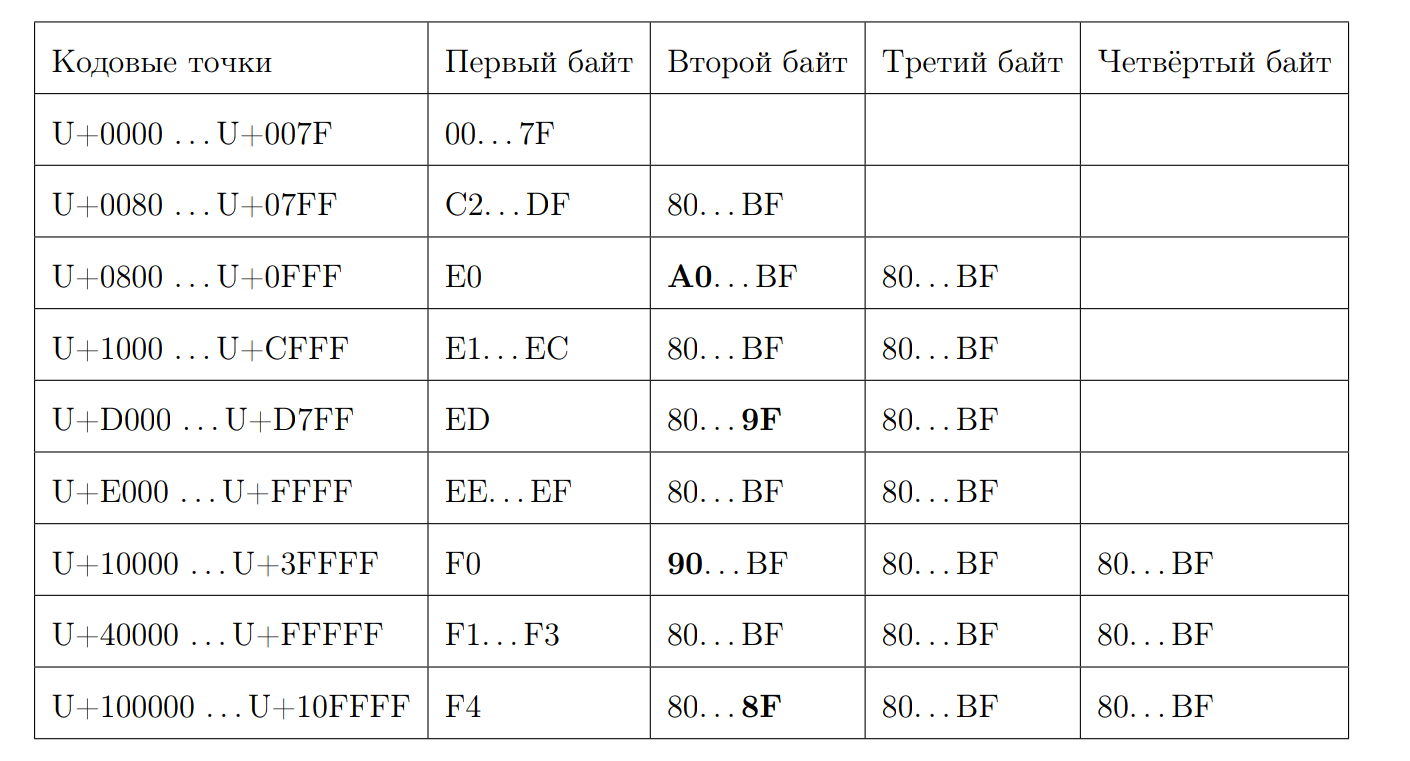
Versuchen wir, die Länge des Codepunkts durch das erste Byte zu berechnen. Hier beginnt etwas Magie. Wieder schreiben wir ein paar Eigenschaften:
- Beginnend bei 0xC und bei 0xD haben 2 Bytes
- 0xC2 = 11 0 00010
- 0xDF = 11 0 11111
- 0xE0 = 111 0 0000
- 0xF4 = 1111 0 100, es gibt nichts weiter als 0xF4, aber wenn es 0xF8 gäbe, würde es eine andere Geschichte geben
- Beantworten Sie 7 abzüglich der Position der ersten Null vom Ende, wenn es sich nicht um ein ASCII-Zeichen handelt
Wir berechnen die Länge:
inline size_t seqLength(const UInt8 first_octet) { if (first_octet < 0x80u) return 1; const auto first_zero = bitScanReverse(static_cast<UInt8>(~first_octet)); return 7 - first_zero; }
Glücklicherweise haben wir Anweisungen auf Lager, die die Anzahl der Nullbits berechnen können, beginnend mit den wichtigsten.
f = __builtin_clz(val)
BitScanReverse berechnen:
unsigned int bitScanReverse(unsigned int x) { return 31 - __builtin_clz(x); }
Versuchen wir, die Länge eines UTF-8-Strings anhand von Codepunkten über SIMD zu berechnen. Betrachten Sie dazu jedes Byte als vorzeichenbehaftete Nummer und beachten Sie die folgenden Eigenschaften:
- 0xBF = -65
- 0x80 = -128
- 0xC2 = -62
- 0x7F = 127
- Alle ersten Bytes sind in [0xC2, 0x7F]
- Alle nicht ersten Bytes befinden sich in [0x80, 0xBF]
Der Algorithmus ist recht einfach. Vergleichen Sie jedes Byte mit -65 und fügen Sie eines hinzu, wenn es größer als diese Zahl ist. Wenn wir SIMD verwenden möchten, ist dies die übliche Last von 16 Bytes aus dem Eingabestream. Dann gibt es einen Byte-Vergleich, der im Falle eines positiven Ergebnisses das Byte 0xFF ergibt, und im Falle eines negativen - 0x00. Dann der pmovmskb , der die hohen Bits jedes Bytes des Registers sammelt. popcnt die Anzahl der Unterstriche erhöht, verwenden wir den intrinsischen popcnt für den popcnt SSE4. Das Schema dieses Algorithmus kann anhand eines Beispiels veranschaulicht werden:

Es stellt sich heraus, dass zusammen mit der Dekomprimierung die Verarbeitung pro Kern ungefähr 1,5 GB / s beträgt.
Die Funktionen heißen:
- lengthUTF8(string) - lengthUTF8(string) die Länge eines korrekt codierten UTF-8-Strings zurück. Etwas wird als ungültig angesehen. Eine Ausnahme wird nicht ausgelöst.
Wir sind noch weiter gegangen, weil wir mit UTF-8-String-Verarbeitung noch mehr Funktionen wollten. Überprüfen Sie beispielsweise die Gültigkeit und wandeln Sie sie in einen gültigen UTF-8-Ausdruck um.
Um die Gültigkeit zu überprüfen, habe ich https://github.com/cyb70289/utf8/ verwendet , angepasst für ClickHouse (hat gerade die Verarbeitung der Schwänze geändert) und eine Geschwindigkeit von 1,22 GB / s im Vergleich zu 900 MB / s für den naiven Algorithmus erhalten . Ich werde den Algorithmus selbst nicht beschreiben, er ist für die Wahrnehmung ziemlich kompliziert.
- isValidUTF8(string) - gibt 1 zurück, wenn die Zeichenfolge korrekt mit UTF-8 codiert ist, andernfalls 0.
- toValidUTF8(string) - toValidUTF8(string) ungültige UTF-8-Zeichen durch das Zeichen (U + FFFD). Alle aufeinanderfolgenden ungültigen Zeichen werden zu einem Ersatzzeichen zusammengefasst. Keine Raketenwissenschaft.
Im Allgemeinen ist es in UTF-8-Leitungen aufgrund des nicht so angenehmen statischen Schemas immer schwierig, etwas zu finden, das gut optimiert ist.
Was weiter?
Ich möchte Sie daran erinnern, dass dies meine These war. Natürlich habe ich sie für 10/10 verteidigt. Wir sind bereits mit ihr nach Highload ++ Siberia gefahren (obwohl es mir so schien, als wäre sie für niemanden von Interesse). Sehen Sie sich die Präsentation an . Mir hat gefallen, dass der praktische Teil der Arbeit zu vielen interessanten Forschungsarbeiten geführt hat. Und hier ist das Diplom selbst. Es hat viele Tippfehler, weil niemand es gelesen hat. :) :)
Im Rahmen der Vorbereitung des Diploms habe ich eine Reihe ähnlicher Arbeiten durchgeführt (Links führen zu Poolanfragen):
- 2-mal optimierte Concat-Funktion ;
- Das einfachste Python-Format für Anfragen erstellt ;
- Beschleunigtes LZ4 um 4% ;
- Ich habe auf SIMD für ARM und PPC64LE großartige Arbeit geleistet .
- Und er beriet einige Studenten des FCS mit Diplomen in ClickHouse.
Am Ende stellte sich heraus, dass nach meiner Erfahrung Jeden Monat versuchte Lesha mich zu singen ClickHouse ist das angenehmste System zum Schreiben von Hochleistungscode mit Dokumentation, Kommentaren, hervorragender Unterstützung für Entwickler und Entwickler. ClickHouse ist wirklich großartig. Sind Sie es leid, JSON-Formate zu ändern? Kommen Sie nach Lesha und fragen Sie nach einer Aufgabe jeder Stufe - er wird sie für Sie bereitstellen, und über das Wochenende werden Sie große Freude daran haben, Code zu schreiben.
Aber bei all den Errungenschaften von ClickHouse und seinem Design geht es wahrscheinlich nicht um sie. Nicht primär in ihnen.
Ich habe 4 Jahre Grundstudium an der FCS absolviert. Im Juni habe ich die HSE mit Auszeichnung abgeschlossen und anderthalb Jahre in einem großartigen Team in Yandex gearbeitet, nachdem ich gut gepumpt war. Die ganze Zeit ohne totale Erfahrung und Eisen Nichts in der Post geschrieben hätte funktioniert. FCN ist sehr cool, wenn man das Maximum daraus zieht. Vielen Dank an Vana Puzyrevsky ivan_puzyrevskiy , Ignat Kolesnichenko , Gleb Evstropov und Max Babenko maxim_babenko für das Treffen in meinem lustigen Abenteuer auf dem FCN. Und auch danke an alle Lehrer, die mir etwas beigebracht haben.