"Wenn Sie die Inschrift" Büffel "auf dem Käfig des Elefanten lesen, trauen Sie Ihren Augen nicht" Kozma Prutkov

In einem früheren Artikel über modellorientiertes Design wurde gezeigt, warum ein Objektmodell benötigt wird, und es wurde bewiesen, dass man ohne dieses Objektmodell von modellbasiertem Design nur als Marketing-Schneesturm sprechen kann, bedeutungslos und gnadenlos. Wenn jedoch ein Objektmodell erscheint, haben kompetente Ingenieure immer eine vernünftige Frage: Welche Beweise gibt es dafür, dass das mathematische Modell eines Objekts einem realen Objekt entspricht?

Ein Beispiel für eine Antwort auf diese Frage findet sich in einem Artikel zum modellorientierten Aufbau eines elektrischen Antriebs. In diesem Artikel betrachten wir ein Beispiel für die Erstellung eines Modells für Luftfahrtklimaanlagen, bei dem die Praxis mit einigen theoretischen allgemeinen Überlegungen verwässert wird.

Erstellen eines zuverlässigen Modells des Objekts. Theorie

Um nicht am Gummi zu ziehen, werde ich Sie sofort über den Algorithmus zum Erstellen eines Modells für modellorientiertes Design informieren. Es hat nur drei einfache Schritte:

Schritt 1. Entwickeln Sie ein System algebraisch-differentieller Gleichungen, die das dynamische Verhalten der simulierten Systeme beschreiben. Es ist einfach, wenn Sie die Physik des Prozesses kennen. Viele Wissenschaftler haben bereits die physikalischen Grundgesetze des Namens Newton, Brenuli, Navier Stokes und anderer Shtangels of Compasses und Rabinovich für uns entwickelt.

Schritt 2. Isolieren Sie im resultierenden System den Satz empirischer Koeffizienten und Eigenschaften des Simulationsobjekts, die aus den Tests erhalten werden können.

Schritt 3. Führen Sie Tests des Objekts durch und passen Sie das Modell gemäß den Ergebnissen von Feldversuchen so an, dass es der Realität mit dem erforderlichen Detaillierungsgrad entspricht.

Wie Sie sehen können, nur zwei drei.

Praktisches Beispiel

Die Klimaanlage (SCR) im Flugzeug ist mit dem automatischen Druckhaltesystem verbunden. Der Druck im Flugzeug sollte immer größer sein als der Außendruck, während die Druckänderungsrate so sein sollte, dass die Piloten und Passagiere nicht Nase und Ohren bluten. Daher ist das Kontrollsystem für das Ein- und Ausströmen von Luft für die Sicherheit wichtig, und teure Testsysteme werden für seine Entwicklung auf den Boden gestellt. Sie erzeugen Temperaturen und Drücke der Flughöhe, reproduzieren Start- und Landemodi auf Flugplätzen unterschiedlicher Höhe. Und die Frage nach der Entwicklung und dem Debuggen von Kontrollsystemen für harte Währungen steigt in vollem Umfang. Wie lange werden wir den Prüfstand fahren, um ein zufriedenstellendes Steuerungssystem zu erhalten? Wenn wir das Kontrollmodell auf das Objektmodell abstimmen, kann der Arbeitszyklus auf dem Prüfstand natürlich erheblich verkürzt werden.

Die Luftfahrtklimaanlage besteht aus den gleichen Wärmetauschern wie jedes andere thermische System. Batterie - es ist auch eine Batterie in Afrika, nur Klimaanlage. Aufgrund der Begrenzung der Startmasse und der Abmessungen des Flugzeugs sind die Wärmetauscher jedoch so kompakt und effizient wie möglich, um so viel Wärme wie möglich von der unteren Masse zu übertragen. Infolgedessen wird die Geometrie ziemlich bizarr. Wie zum Beispiel im betrachteten Fall. 1 zeigt einen Plattenwärmetauscher, bei dem eine Membran zwischen den Platten verwendet wird, um die Wärmeübertragung zu verbessern. Heißes und kaltes Kühlmittel wechseln sich in den Kanälen ab, während die Strömungsrichtung quer verläuft. Ein Kühlmittel wird dem Frontalschnitt zugeführt, das andere der Seite.

Um das SCR-Steuerungsproblem zu lösen, müssen wir wissen, wie viel Wärme in einem solchen Wärmetauscher pro Zeiteinheit von einem Medium auf ein anderes übertragen wird. Davon hängt die Änderungsrate der Temperatur ab, die wir regulieren.

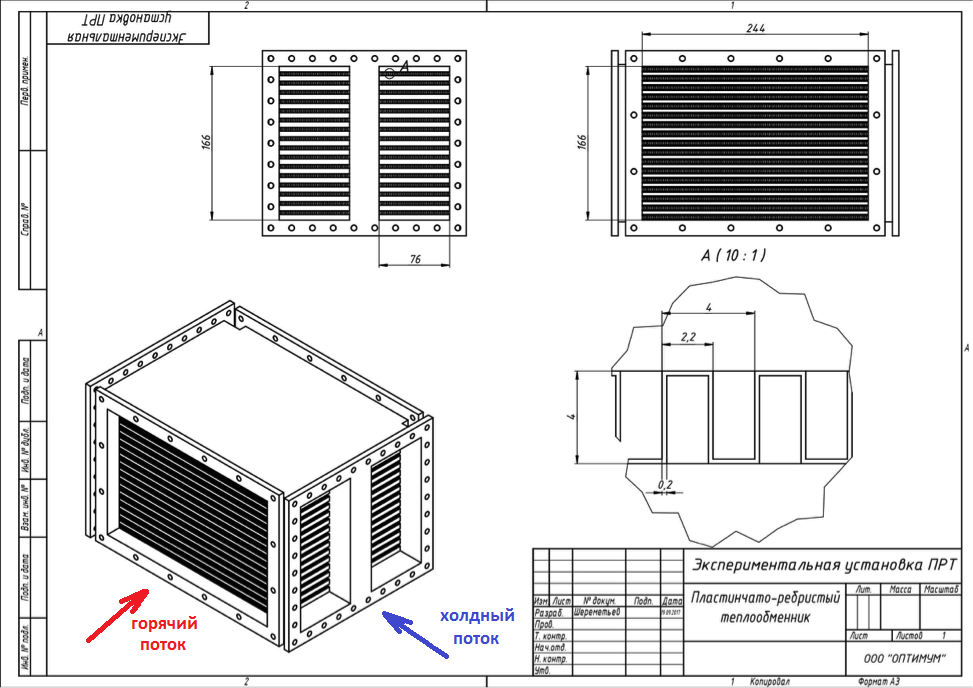
Abbildung 1. Diagramm des Flugzeugwärmetauschers.

Modellierungsprobleme. Hydraulikteil

Auf den ersten Blick ist die Aufgabe recht einfach, es ist notwendig, den Massenstrom durch die Kanäle des Wärmetauschers und den Wärmestrom zwischen den Kanälen zu berechnen.
Der Massenstrom des Kühlmittels in den Kanälen wird nach der Bernoulli-Formel berechnet:

wo:
ΔP ist der Druckabfall zwischen zwei Punkten;
ξ ist der Reibungskoeffizient des Kühlmittels;
L ist die Länge des Kanals;
d ist der hydraulische Durchmesser des Kanals;
ρ ist die Dichte des Kühlmittels;
ω ist die Kühlmittelgeschwindigkeit im Kanal.

Für einen Kanal beliebiger Form wird der hydraulische Durchmesser nach folgender Formel berechnet:

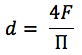
wo:
F ist der Bereich der Bohrung;
P - benetzter Kanalumfang.

Der Reibungskoeffizient wird nach empirischen Formeln berechnet und hängt von der Strömungsgeschwindigkeit und den Eigenschaften des Kühlmittels ab. Für unterschiedliche Geometrien ergeben sich unterschiedliche Abhängigkeiten, beispielsweise die Formel für turbulente Strömung in glatten Rohren:

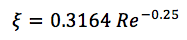
wo:
Re ist die Reynolds-Nummer.

Für den Durchfluss in flachen Kanälen kann die folgende Formel verwendet werden:

Aus der Bernoulli-Formel können Sie den Druckabfall für eine bestimmte Geschwindigkeit berechnen oder umgekehrt die Geschwindigkeit des Kühlmittels im Kanal basierend auf einem bestimmten Druckabfall berechnen.

Wärmeübertragung

Der Wärmefluss zwischen Kühlmittel und Wand wird nach folgender Formel berechnet:

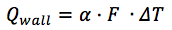
wo:
α [W / (m2 × Grad)] - Wärmeübergangskoeffizient;
F ist der Bereich der Bohrung.

Für Probleme des Kühlmittelflusses in Rohren wurde eine ausreichende Anzahl von Studien durchgeführt, und es gibt viele Berechnungsmethoden. In der Regel kommt es auf empirische Abhängigkeiten für den Wärmeübergangskoeffizienten α [W / (m2 × Grad)] an.

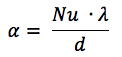
wo:
Nu ist die Nusselt-Nummer,
λ ist die Wärmeleitfähigkeit der Flüssigkeit [W / (m × Grad)]
d ist der hydraulische (äquivalente) Durchmesser.

Empirische Kriterienabhängigkeiten werden verwendet, um die Nusselt-Zahl (Kriterium) zu berechnen. Beispielsweise sieht die Formel zur Berechnung der Nusselt-Zahl eines Rundrohrs folgendermaßen aus:

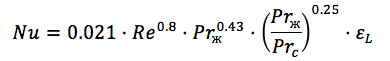
Hier sehen wir bereits die Reynolods-Zahl, die Prandtl-Zahl bei Wandtemperatur und Flüssigkeitstemperatur und den Ungleichmäßigkeitskoeffizienten. ( Quelle )

Für Wellplattenwärmetauscher ist die Formel ähnlich ( Quelle ):

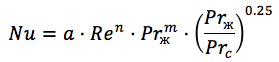
wo:
n = 0,73 m = 0,43 für eine turbulente Strömung,
Koeffizient a - variiert zwischen 0,065 und 0,6 in Abhängigkeit von der Anzahl der Platten und dem Durchflussregime.

Beachten Sie, dass dieser Koeffizient nur für einen Punkt im Stream berechnet wird. Für den nächsten Punkt haben wir eine andere Flüssigkeitstemperatur (sie hat sich erwärmt oder abgekühlt), eine andere Wandtemperatur und dementsprechend schweben alle Reynolds- und Prandtl-Zahlen.

An diesem Punkt wird jeder Mathematiker sagen, dass es unmöglich ist, genau das System zu berechnen, in dem sich der Koeffizient zehnmal ändert, und er wird Recht haben.

Jeder praktizierende Ingenieur wird sagen, dass jeder Wärmetauscher in der Herstellung anders ist und es unmöglich ist, Systeme zu berechnen, und es wird auch richtig sein.

Aber was ist mit modellorientiertem Design? Ist alles weg?

Fortgeschrittene Verkäufer westlicher Software an diesem Ort werden Sie mit einem Supercomputer und 3D-Berechnungssystemen wie "in keiner Weise ohne" koppeln. Und Sie müssen die Berechnung für einen Tag ausführen, um die Temperaturverteilung für 1 Minute zu erhalten.

Es ist klar, dass dies nicht unsere Option ist. Wir müssen das Steuerungssystem debuggen, wenn nicht in Echtzeit, dann zumindest in absehbarer Zukunft.

Poke-Methode

Ein Wärmetauscher wird hergestellt, eine Reihe von Tests wird durchgeführt und eine Tabelle des Wirkungsgrades der stationären Temperatur wird bei den gegebenen Durchflussraten erstellt. Einfach, schnell und zuverlässig, wie die Daten aus den Tests erhalten.

Der Nachteil dieses Ansatzes besteht darin, dass es keine dynamischen Eigenschaften des Objekts gibt. Ja, wir wissen, wie hoch der stationäre Wärmefluss sein wird, aber wir wissen nicht, wie lange er beim Umschalten von einem Betriebsmodus in einen anderen hergestellt wird.

Nachdem wir die notwendigen Eigenschaften berechnet haben, richten wir das Steuerungssystem direkt während der Tests ein, was wir von Anfang an vermeiden möchten.

Modellorientierter Ansatz

Um ein Modell eines dynamischen Wärmetauschers zu erstellen, müssen Testdaten verwendet werden, um Unsicherheiten in empirischen Berechnungsformeln - Nusselt-Zahl und hydraulischer Widerstand - zu beseitigen.

Die Entscheidung ist einfach, wie alle genial. Wir nehmen die empirische Formel, führen Experimente durch und bestimmen den Wert des Koeffizienten a, wodurch die Unsicherheit in der Formel beseitigt wird.

Sobald wir einen bestimmten Wert des Wärmeübergangskoeffizienten haben, werden alle anderen Parameter durch die physikalischen Grundgesetze der Konservierung bestimmt. Die Temperaturdifferenz und der Wärmeübergangskoeffizient bestimmen die pro Zeiteinheit auf den Kanal übertragene Energiemenge.

Bei Kenntnis des Energieflusses ist es möglich, die Gleichungen zur Erhaltung der Energiemasse und des Impulses für das Kühlmittel im Hydraulikkanal zu lösen. Zum Beispiel:

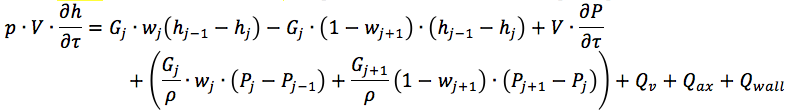
In unserem Fall bleibt der Wärmefluss zwischen Wand und Kühlmittel - Qwall - unbestimmt. Weitere Details finden Sie hier ...

Und auch die Gleichung für die Temperaturableitung für die Kanalwand:

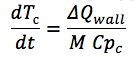
wo:
ΔQ- _Wand - die Differenz zwischen dem ein- und ausgehenden Fluss zur Kanalwand;
M ist die Masse der Kanalwand;
C _pc ist die Wärmekapazität des Wandmaterials.

Modellgenauigkeit

Wie oben erwähnt, haben wir im Wärmetauscher eine Temperaturverteilung über die Oberfläche der Platte. Für den stationären Wert kann man den Durchschnitt über die Platten nehmen und ihn verwenden, der den gesamten Wärmetauscher als einen einzigen konzentrierten Punkt darstellt, an dem die Wärmeübertragung über die gesamte Oberfläche des Wärmetauschers bei gleicher Temperaturdifferenz erfolgt. Bei transienten Modi funktioniert diese Annäherung jedoch möglicherweise nicht. Das andere Extrem ist, mehrere hunderttausend Punkte zu machen und den Supercomputer zu laden, was auch nicht zu uns passt, da die Aufgabe darin besteht, das Steuerungssystem in Echtzeit oder besser schneller zu konfigurieren.

Es stellt sich die Frage, wie viele Abschnitte Sie benötigen, um den Wärmetauscher zu brechen, um eine akzeptable Genauigkeit und Berechnungsgeschwindigkeit zu erzielen.

Wie immer zufällig hatte ich ein Modell eines Aminwärmetauschers zur Hand. Der Wärmetauscher ist ein Rohr, Heizmedium fließt in die Rohre und wird zwischen den Gruben erwärmt. Um die Aufgabe zu vereinfachen, kann das gesamte Rohr des Wärmetauschers als ein äquivalentes Rohr dargestellt werden, und das Rohr selbst kann als ein Satz diskreter Entwurfszellen dargestellt werden, in denen jeweils ein Punktmodell der Wärmeübertragung berechnet wird. Das Modelldiagramm einer einzelnen Zelle ist in Abbildung 2 dargestellt. Der Heißluftkanal und der Kaltluftkanal sind durch eine Wand verbunden, die eine Wärmeübertragung zwischen den Kanälen ermöglicht.

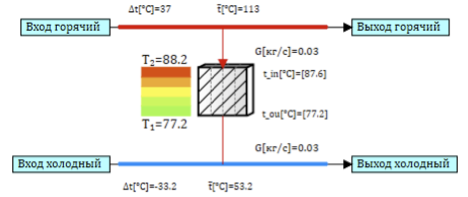
Abbildung 2. Modell der Wärmetauscherzelle.

Das Rohrwärmetauschermodell ist leicht anpassbar. Sie können nur einen Parameter ändern - die Anzahl der Abschnitte entlang der Rohrlänge und die Berechnungsergebnisse für verschiedene Partitionen anzeigen. Wir werden verschiedene Optionen berechnen, beginnend mit der Aufteilung in 5 Längenpunkte (Abb. 3) und bis zu 100 Längenpunkte (Abb. 4).

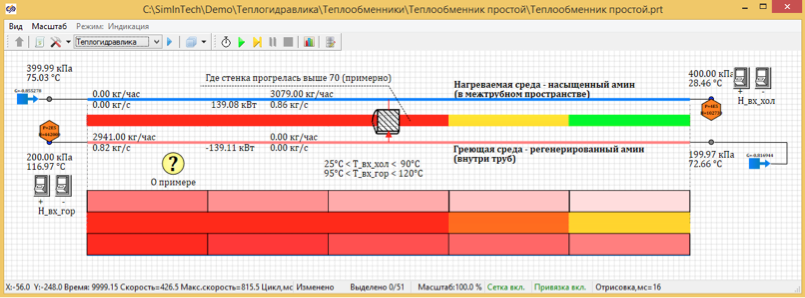
Abbildung 3. Stationäre Temperaturverteilung von 5 Auslegungspunkten.

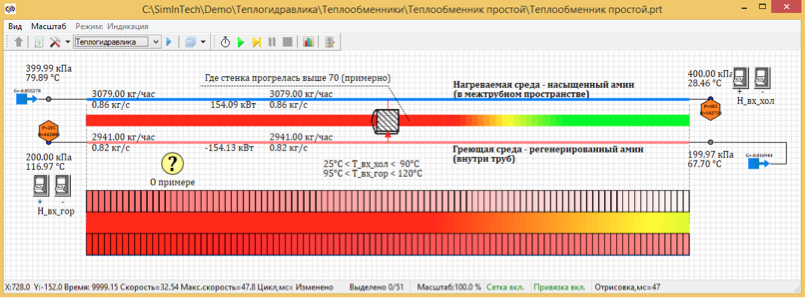
Abbildung 4. Stationäre Temperaturverteilung von 100 Auslegungspunkten.

Als Ergebnis von Berechnungen stellte sich heraus, dass die stationäre Temperatur geteilt durch 100 Punkte 67,7 Grad beträgt. Und wenn in 5 berechnete Punkte unterteilt, beträgt die Temperatur 72, 66 ° C.

Außerdem wird die Berechnungsgeschwindigkeit relativ zur Echtzeit im unteren Teil des Fensters angezeigt.
Mal sehen, wie sich die stationäre Temperatur und die Berechnungsgeschwindigkeit in Abhängigkeit von der Anzahl der Auslegungspunkte ändern. Der Unterschied der stationären Temperaturen bei Berechnungen mit einer unterschiedlichen Anzahl von Berechnungszellen kann verwendet werden, um die Genauigkeit des Ergebnisses zu bewerten.

Tabelle 1. Die Abhängigkeit von Temperatur und Berechnungsgeschwindigkeit von der Anzahl der Auslegungspunkte entlang der Länge des Wärmetauschers.

Wenn wir diese Tabelle analysieren, können wir die folgenden Schlussfolgerungen ziehen:

• Die Berechnungsgeschwindigkeit nimmt proportional zur Anzahl der Auslegungspunkte im Wärmetauschermodell ab.
• Die Änderung der Berechnungsgenauigkeit erfolgt exponentiell. Wenn die Anzahl der Punkte zunimmt, nimmt die Verfeinerung bei jeder nachfolgenden Erhöhung ab.

Im Fall eines Plattenwärmetauschers mit einem Querstromwärmeträger wie in Abbildung 1 ist die Erstellung eines äquivalenten Modells aus elementaren Konstruktionszellen etwas kompliziert. Wir müssen die Zellen so verbinden, dass der Querfluss organisiert wird. Bei 4 Zellen sieht die Schaltung wie in Abbildung 5 dargestellt aus.

Der Kühlmittelstrom ist entlang des heißen und kalten Zweigs in zwei Kanäle unterteilt. Die Kanäle werden durch thermische Strukturen verbunden, so dass das Kühlmittel beim Durchgang durch den Kanal Wärme mit verschiedenen Kanälen austauscht. Bei der Simulation der Querströmung fließt der heiße Wärmeträger in jedem Kanal von links nach rechts (siehe Abb. 5) und tauscht nacheinander Wärme mit den Kanälen des kalten Wärmeträgers aus, der von unten nach oben verläuft (siehe Abb. 5). Der heißeste Punkt befindet sich in der oberen linken Ecke, da der heiße Wärmeträger Wärme mit dem bereits erwärmten Kühlmittel des Kaltkanals austauscht. Und das kälteste unten rechts, wo das kalte Kühlmittel Wärme mit dem heißen Kühlmittel austauscht, das bereits im ersten Abschnitt abgekühlt ist.

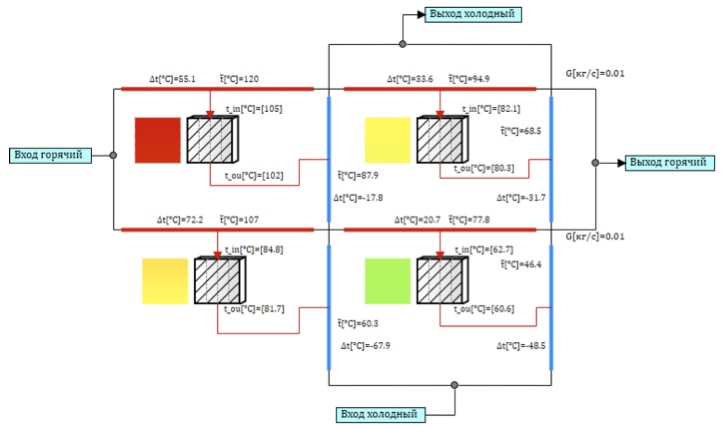
Abbildung 5. Ein Cross-Flow-Modell von 4 Entwurfszellen.

Ein solches Modell für einen Plattenwärmetauscher berücksichtigt nicht den Wärmeübergang zwischen den Zellen aufgrund der Wärmeleitfähigkeit und berücksichtigt nicht das Mischen des Kühlmittels, da jeder Kanal isoliert ist.

In unserem Fall verringert die letztere Einschränkung jedoch nicht die Genauigkeit, da bei der Konstruktion des Wärmetauschers die Wellmembran die Strömung entlang des Kühlmittels in viele isolierte Kanäle aufteilt (siehe Abb. 1). Mal sehen, was mit der Genauigkeit der Berechnung passiert, wenn ein Plattenwärmetauscher mit einer Zunahme der Anzahl der Entwurfszellen modelliert wird.

Für die Genauigkeitsanalyse verwenden wir zwei Optionen, um den Wärmetauscher in die Entwurfszelle zu unterteilen:

1. Jede quadratische Zelle enthält zwei hydraulische (kalte und heiße Strömungen) und ein thermisches Element. (siehe Abbildung 5)
2. Jede quadratische Zelle enthält sechs hydraulische Elemente (drei Abschnitte in heißen und kalten Strömungen) und drei thermische Elemente.

Im letzteren Fall verwenden wir zwei Arten von Verbindungen:

• Gegenstrom von kalten und heißen Strömen;
• zugehöriger Fluss von kaltem und heißem Fluss.

Der entgegenkommende Strom erhöht den Wirkungsgrad im Vergleich zum Querstrom und der zugehörige Strom nimmt ab. Bei einer großen Anzahl von Zellen erfolgt eine Flussmittelung, und alles nähert sich dem tatsächlichen Querfluss um ihn herum an (siehe Abbildung 6).

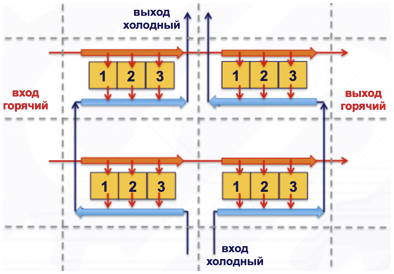
Abbildung 6. Ein Cross-Flow-Modell von vier Zellen mit drei Elementen.

Abbildung 7 zeigt die Ergebnisse einer stationären stationären Temperaturverteilung im Wärmetauscher bei der Luftzufuhr über eine heiße Leitung mit einer Temperatur von 150 ° C und entlang einer kalten Leitung mit 21 ° C für verschiedene Optionen zur Aufteilung des Modells. Die Farbe und die Zahlen auf der Zelle spiegeln die durchschnittliche Wandtemperatur in der Zelle wider.

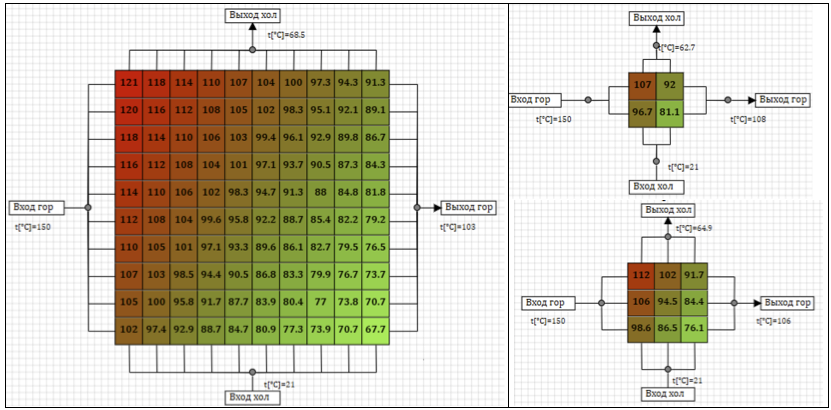
Abbildung 7. Steady-State-Temperaturen für verschiedene Berechnungsschemata.

Tabelle 2 zeigt die stationäre Temperatur der erwärmten Luft nach dem Wärmetauscher in Abhängigkeit von der Aufteilung des Wärmetauschermodells in Zellen.

Tabelle 2. Temperaturabhängigkeit von der Anzahl der Auslegungszellen im Wärmetauscher.

Mit zunehmender Anzahl von Rechenzellen im Modell steigt die endgültige stationäre Temperatur an. Die Differenz zwischen der stationären Temperatur an verschiedenen Partitionen kann als Indikator für die Berechnungsgenauigkeit angesehen werden. Es ist ersichtlich, dass mit einer Zunahme der Anzahl von Berechnungszellen die Temperatur an die Grenze tendiert und die Zunahme der Genauigkeit nicht proportional zur Anzahl von Berechnungspunkten ist.

Die Frage stellt sich, aber welche Genauigkeit des Modells brauchen wir?

Die Antwort auf diese Frage hängt vom Zweck unseres Modells ab. Da es in diesem Artikel um modellorientiertes Design geht, erstellen wir ein Modell zur Optimierung des Steuerungssystems. Dies bedeutet, dass die Genauigkeit des Modells mit der Genauigkeit der im System verwendeten Sensoren vergleichbar sein muss.

In unserem Fall wird die Temperatur mit einem Thermoelement gemessen, bei dem die Genauigkeit ± 2,5 ° C beträgt. Eine höhere Genauigkeit zum Einstellen des Steuerungssystems ist nutzlos. Unser echtes Steuerungssystem "wird es einfach nicht sehen". Wenn wir also annehmen, dass die Grenztemperatur mit einer unendlichen Anzahl von Partitionen 70 ° C beträgt, ist ein Modell, das uns mehr als 67,5 ° C liefert, von ausreichender Genauigkeit. Alle Modelle mit 3 Punkten in der Berechnungszelle und Modelle sind größer als 5 x 5 mit einem Punkt in der Zelle. (In Tabelle 2 grün hervorgehoben)

Dynamische Betriebsarten

Um den dynamischen Modus zu bewerten, bewerten wir den Prozess der Temperaturänderung an den heißesten und kältesten Stellen der Wärmetauscherwand für verschiedene Entwurfsschemata. (siehe Abb. 8)


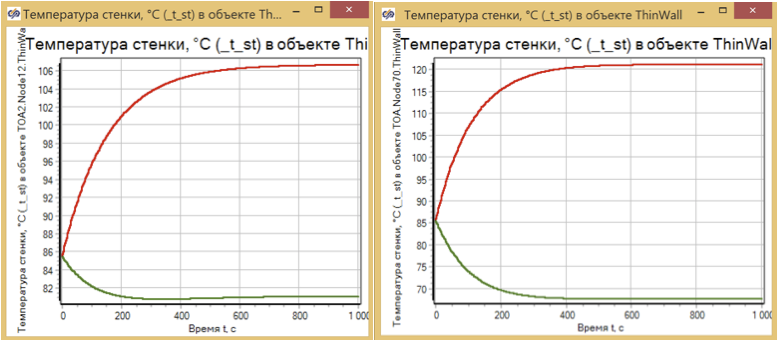
Abbildung 8. Aufwärmen des Wärmetauschers. Modelle mit den Abmessungen 2x2 und 10x10.

Es ist ersichtlich, dass die Zeit des Übergangsprozesses und seine Natur praktisch nicht von der Anzahl der berechneten Zellen abhängen und ausschließlich durch die Masse des erhitzten Metalls bestimmt werden.

Wir schließen daraus, dass für eine ehrliche Simulation des Wärmetauschers in den Modi von 20 bis 150 ° C mit der vom SCR-Steuerungssystem geforderten Genauigkeit etwa 10 bis 20 berechnete Punkte ausreichen.

Experimentieren Sie mit dem Aufbau eines dynamischen Modells

, , , , , .

, , . 9 . , , , .

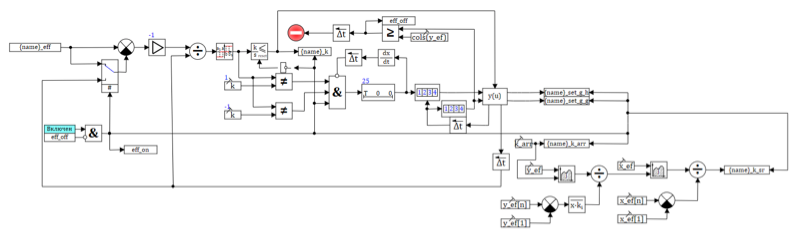
9. .

a . , ( ) . , 0.492 0.655

0.6, , , .

– :

:
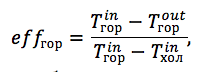
eff – ;
T ⁱⁿ – ;
T ^out – ;
T ⁱⁿ – .

3 .

3. %

. , , , , .

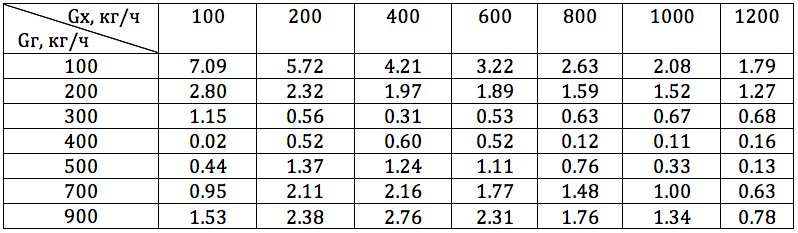
, 10 .

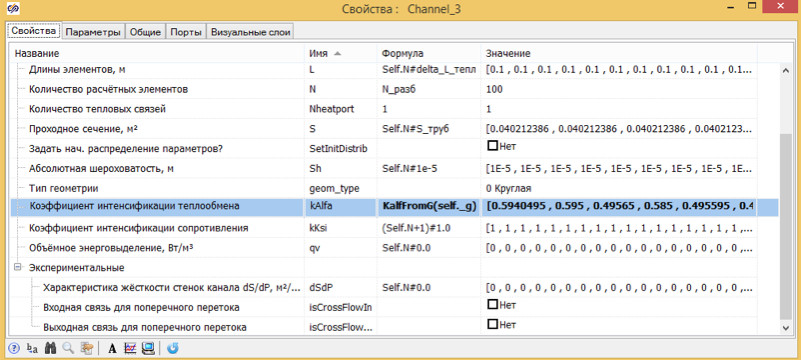
10. .

Schlussfolgerungen

• - .
  
• .
  
• .
  
• - !

. .