Serie "Weißes Rauschen zeichnet ein schwarzes Quadrat"
Die Geschichte des Zyklus dieser Veröffentlichungen beginnt mit der Tatsache, dass in
G.Sekeys Buch
„Paradoxe in der Wahrscheinlichkeits- und mathematischen Statistik“ (
S. 43 ) die folgende Aussage entdeckt wurde:

Abb. 1.
Der Analyse zufolge hat der Kommentar zu den ersten Veröffentlichungen (
Teil 1 ,
Teil 2 ) und die anschließende Argumentation die Idee gereift, diesen Satz in einer visuelleren Form darzustellen.
Die meisten Community-Mitglieder kennen das Pascal-Dreieck als Folge der binomialen Wahrscheinlichkeitsverteilung und vieler verwandter Gesetze. Um den Mechanismus der Bildung des Pascalschen Dreiecks zu verstehen, werden wir es mit der Entfaltung der Strömungen seiner Bildung genauer erweitern. Im Pascal-Dreieck werden Knoten im Verhältnis 0 und 1 gebildet (siehe Abbildung unten).
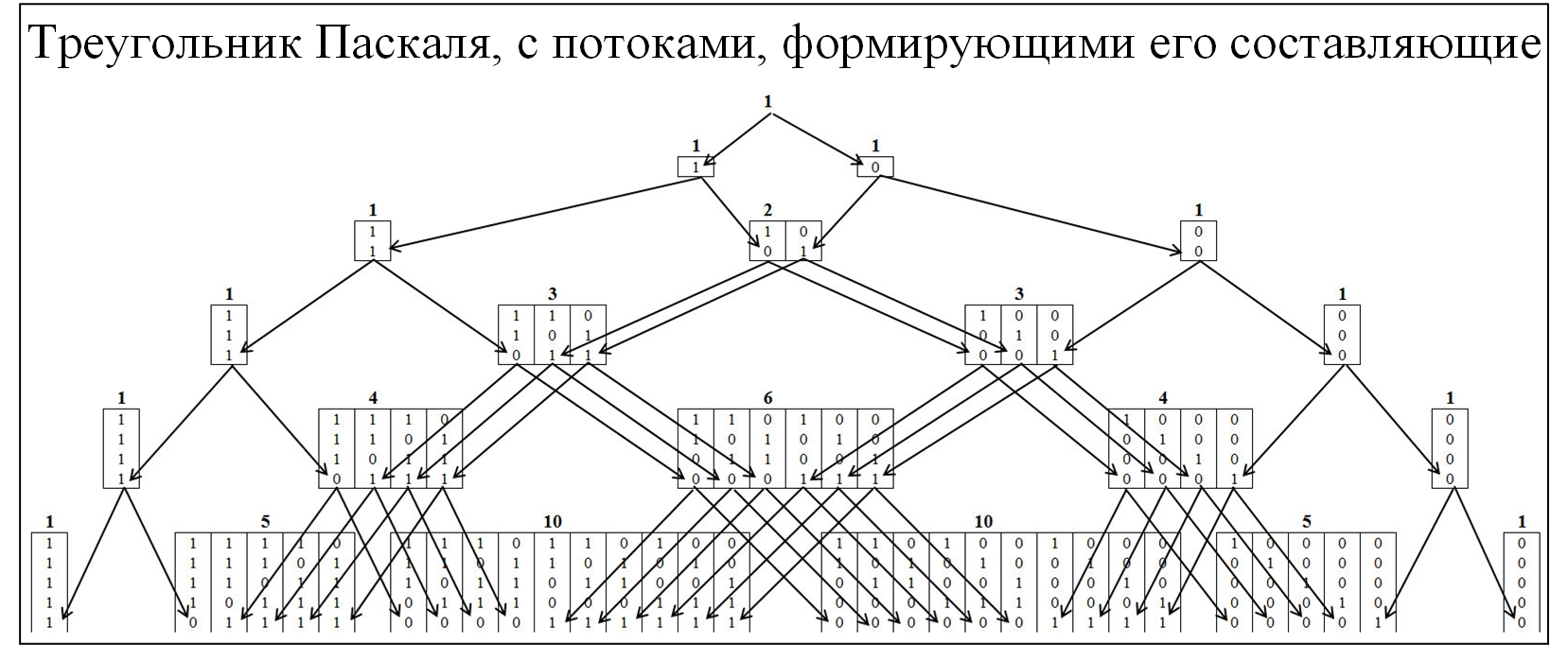
Abb. 2.
Um das Erds-Renyi-Theorem zu verstehen, werden wir ein ähnliches Modell erstellen, aber die Knoten werden aus den Werten gebildet, in denen die größten Ketten vorhanden sind, die nacheinander aus denselben Werten bestehen. Das Clustering wird gemäß der folgenden Regel durchgeführt: Ketten 01/10 zu Cluster „1“; Kette 00/11, um "2" zu gruppieren; Ketten 000/111, um "3" usw. zu gruppieren. In diesem Fall teilen wir die Pyramide in zwei symmetrische Komponenten (Abbildung 3).

Abb. 3.
Das erste, was auffällt, ist, dass alle Bewegungen von einem niedrigeren zu einem höheren Cluster stattfinden und umgekehrt nicht. Dies ist natürlich, denn wenn sich eine Kette der Größe j gebildet hat, kann sie nicht mehr verschwinden.
Durch die Bestimmung des Algorithmus zur Konzentration von Zahlen gelang es uns, die folgende Wiederholungsformel zu erhalten, deren Mechanismus in den Abbildungen 4-6 dargestellt ist.
Bezeichnen Sie die Elemente, in denen sich die Zahlen konzentrieren. Dabei ist n die Anzahl der Zeichen in der Anzahl (Anzahl der Bits) und die Länge der maximalen Kette ist m. Und jedes Element erhält einen Index n; mJ.
Bezeichnen Sie, dass die Anzahl der Elemente von n; mJ nach n + 1; m + 1J, n; mjn + 1; m + 1 übergeben wurde.

Abb. 4.
Abbildung 4 zeigt, dass es für den ersten Cluster nicht schwierig ist, die Werte jeder Zeile zu bestimmen. Und diese Abhängigkeit ist gleich:

Abb. 5.
Wir bestimmen für den zweiten Cluster mit der Kettenlänge m = 2, Abbildung 6.
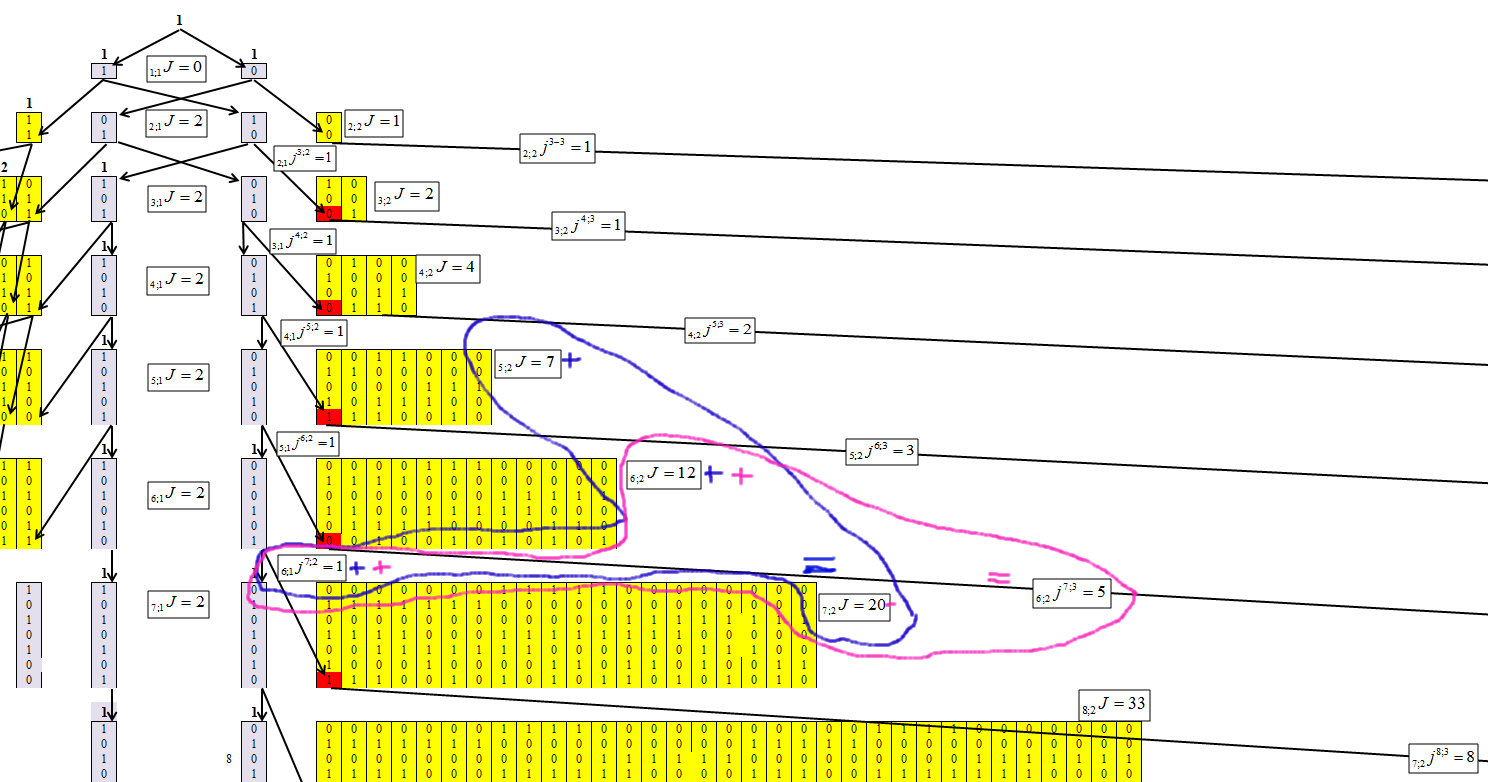
Abb. 6.
Abbildung 6 zeigt, dass für den zweiten Cluster die Abhängigkeit gleich ist:

Abb. 7.
Wir bestimmen für den dritten Cluster mit der Kettenlänge m = 3, Abbildung 8.
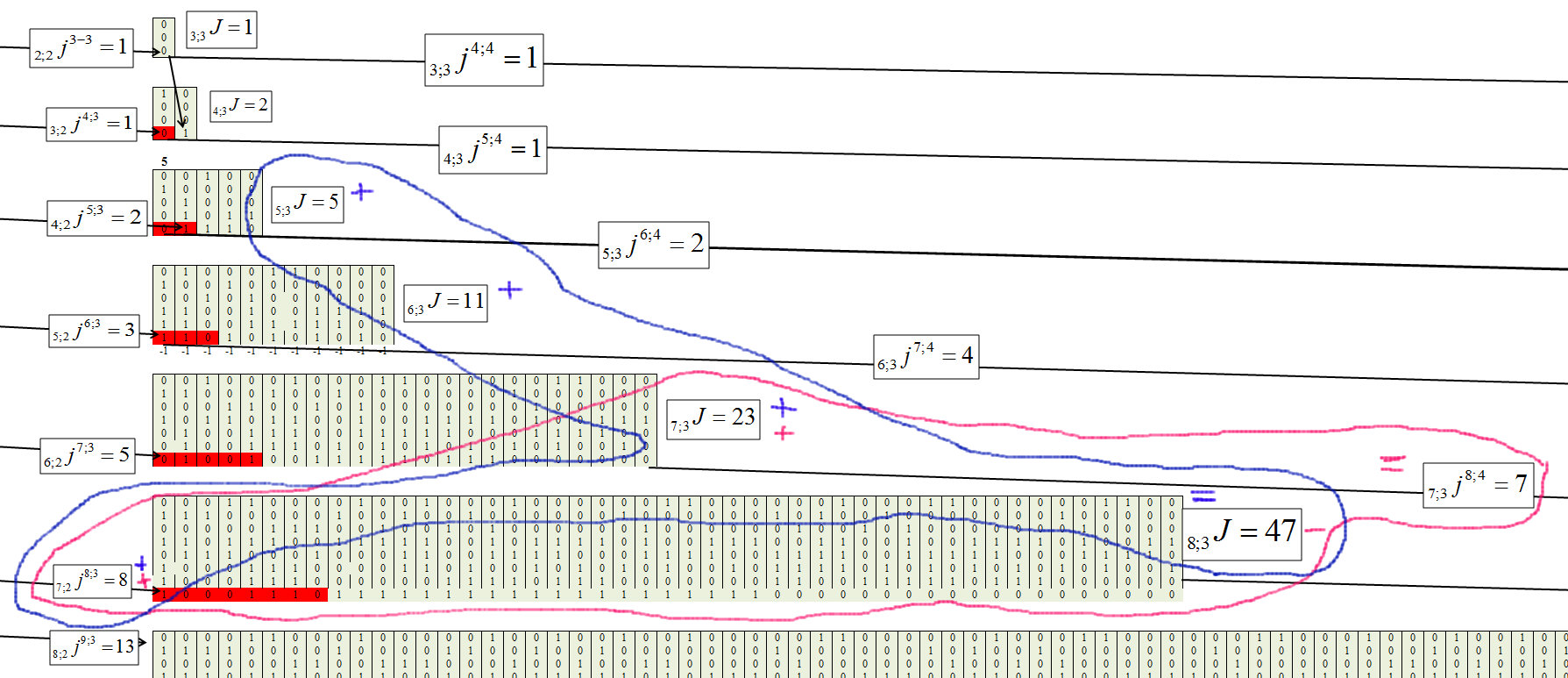
Abb. 8.

Abb. 9.
Die allgemeine Formel jedes Elements hat folgende Form:

Abb. 10.

Abb. 11.
Überprüfung
Zur Überprüfung verwenden wir die Eigenschaft dieser Sequenz, die in Abbildung 12 dargestellt ist. Sie besteht darin, dass die letzten Elemente einer Zeile ab einer bestimmten Position für alle Zeilen mit zunehmender Zeilenlänge einen einzigen Wert annehmen.
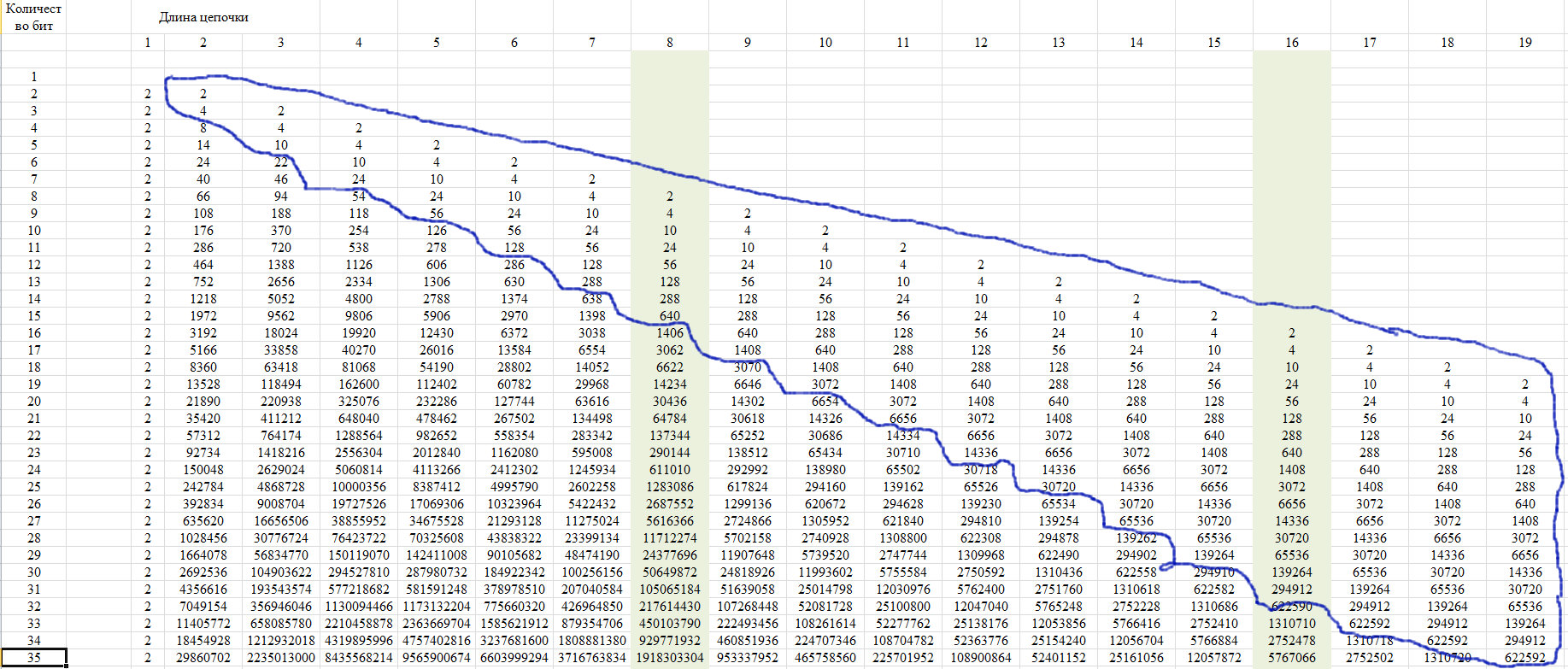
Abb. 12.
Diese Eigenschaft beruht auf der Tatsache, dass bei einer Kettenlänge von mehr als der Hälfte der gesamten Reihe nur eine solche Kette möglich ist. Wir zeigen dies im Diagramm von Abbildung 13.

Abb. 13.
Dementsprechend erhalten wir für Werte von k <n-2 die Formel:
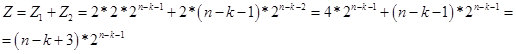
Abb. 14.
Tatsächlich ist der Wert von Z die potentielle Anzahl von Zahlen (Optionen in einer Folge von n Bits), die eine Kette von k identischen Elementen enthalten. Und gemäß der Wiederholungsformel bestimmen wir die Anzahl der Zahlen (Optionen in einer Folge von n Bits), in denen die Kette von k identischen Elementen am größten ist. Im Moment gehe ich davon aus, dass der Wert Z virtuell ist. Daher geht es in der Region n / 2 in den realen Raum über. In Abbildung 15 ein Bildschirm mit Berechnungen.

Abb. 15.
Lassen Sie uns ein Beispiel für ein 256-Bit-Wort zeigen, das mit diesem Algorithmus bestimmt werden kann.

Abb. 16.
Wenn durch die Standards von 99,9% Zuverlässigkeit für den GSPCH bestimmt, muss der 256-Bit-Schlüssel aufeinanderfolgende Ketten identischer Zeichen mit der Nummer 5 bis 17 enthalten. Das heißt, gemäß den Standards für den GSPCH, damit er die Anforderung der Ähnlichkeit der Zufälligkeit mit 99,9% Zuverlässigkeit erfüllt, GSPCH sollte in 2000 Tests (Ausgabe eines Ergebnisses in Form einer 256-Bit-Binärzahl) nur ein Ergebnis liefern, bei dem die maximale Serienlänge dieselben Werte aufweist: entweder weniger als 4 oder mehr als 17.
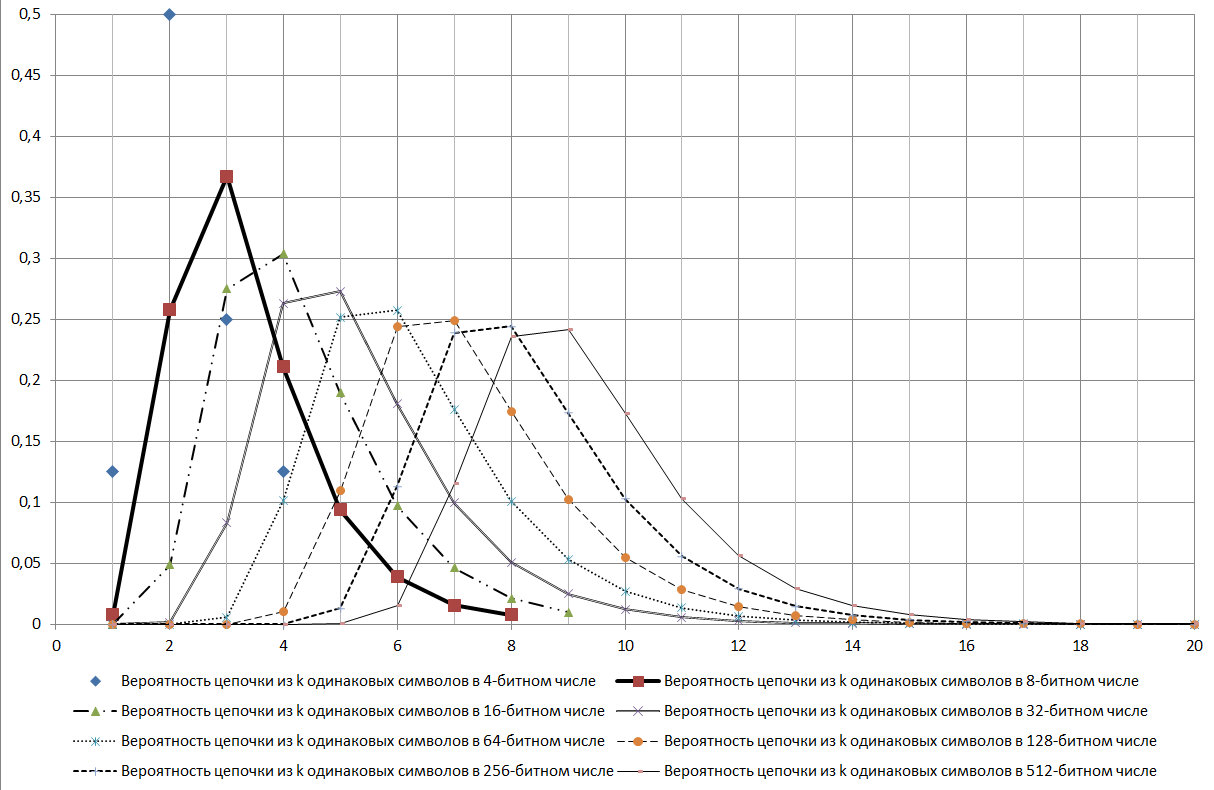
Abb. 17.
Wie aus dem in Abbildung 17 gezeigten Diagramm ersichtlich ist, ist die log2N-Kette ein Modus für die betrachtete Verteilung.
Während der Studie wurden viele Anzeichen für verschiedene Eigenschaften dieser Sequenz gefunden. Hier sind einige davon:
- es sollte durch das Chi-Quadrat-Kriterium gut getestet werden;
- gibt Anzeichen für die Existenz fraktaler Eigenschaften;
- kann ein gutes Kriterium für die Identifizierung verschiedener zufälliger Prozesse sein.
Und viele weitere Verbindungen.
Geprüft, ob eine solche Sequenz in der Online
-Enzyklopädie der ganzzahligen Sequenzen (OEIS) (Online-Enzyklopädie der ganzzahligen Sequenzen) in der Sequenznummer
A006980 vorhanden ist , wird auf die Veröffentlichung
JL Yucas, Counting Special Sets of Binary Lyndon Words, Ars Combin , verwiesen
. 31 (1991), p. 21-29 , wo die Sequenz auf Seite 28 (in der Tabelle) gezeigt wird. In der Veröffentlichung sind die Zeilen 1 weniger nummeriert, aber die Werte sind gleich. Im Allgemeinen handelt die Veröffentlichung von
Lyndons Worten , das heißt, es ist durchaus möglich, dass der Forscher nicht einmal vermutete, dass diese Reihe mit diesem Aspekt zusammenhängt.
Kehren wir zum Erds-Renyi-Theorem zurück. Nach den Ergebnissen dieser Veröffentlichung kann gesagt werden, dass sich dieser Satz in der vorgestellten Formulierung auf den allgemeinen Fall bezieht, der durch den Muavre-Laplace-Satz bestimmt wird. Und der angegebene Satz in dieser Formulierung kann kein eindeutiges Kriterium für die Zufälligkeit einer Reihe sein. Die Fraktalität, und für diesen Fall wird ausgedrückt, dass Ketten der angegebenen Länge mit Ketten längerer Länge kombiniert werden können, erlaubt es uns jedoch nicht, diesen Satz so eindeutig abzulehnen, da eine Ungenauigkeit in der Formulierung möglich ist. Ein Beispiel ist die Tatsache, dass, wenn für eine 256-Bit-Wahrscheinlichkeit einer Zahl, bei der die maximale Kette von 8 Bits 0,244235 beträgt, in Verbindung mit anderen längeren Sequenzen die Wahrscheinlichkeit, dass eine Zahl von 8 Bits in einer Zahl vorhanden ist, bereits - 0,490234375. Das heißt, es gibt bisher keine eindeutige Möglichkeit, diesen Satz abzulehnen. Dieser Satz passt jedoch recht gut zu einem anderen Aspekt, der später gezeigt wird.
Praktische Anwendung
Schauen wir uns das Beispiel des VDG-Benutzers an:
„... Die dendritischen Zweige eines Neurons können als Bitfolge dargestellt werden. Ein Zweig und dann das gesamte Neuron wird ausgelöst, wenn eine Synapsenkette an einer ihrer Stellen aktiviert wird. Das Neuron hat die Aufgabe, nicht auf weißes Rauschen zu reagieren. Soweit ich mich an Numenty erinnere, beträgt die Mindestlänge der Kette 14 Synapsen im pyramidenförmigen Neuron mit seinen 10 000 Synapsen. Und nach der Formel erhalten wir: Log_ {2} 10000 = 13.287. Das heißt, Ketten mit einer Länge von weniger als 14 werden aufgrund von natürlichem Rauschen auftreten, aber das Neuron nicht aktivieren. Es ist perfekt richtig gelegt .
"Wir werden ein Diagramm erstellen, aber unter Berücksichtigung der Tatsache, dass Excel keine Werte größer als 2 ^ 1024 berücksichtigt, beschränken wir uns auf die Anzahl der Synapsen 1023 und interpolieren das Ergebnis durch Kommentieren, wie in Abbildung 18 gezeigt.

Abb. 18.
Es gibt ein biologisches neuronales Netzwerk, das ausgelöst wird, wenn eine Kette von m = log2N = 11 kompiliert wird. Diese Kette ist ein Modalwert, und ein Schwellenwert, die Wahrscheinlichkeit einer Änderung der Situation von 0,78, wird erreicht. Und die Fehlerwahrscheinlichkeit beträgt 1 - 0,78 = 0,22. Angenommen, eine Kette von 9 Sensoren funktioniert, wobei die Wahrscheinlichkeit zur Bestimmung des Ereignisses 0,37 beträgt und die Fehlerwahrscheinlichkeit 1 - 0,37 = 0,63 beträgt. Das heißt, um eine Verringerung der Fehlerwahrscheinlichkeit von 0,63 auf 0,37 zu erreichen, müssen 3,33 Ketten mit 9 Elementen funktionieren. Die Differenz zwischen 11 und 9 Elementen ist von der 2. Ordnung, dh 2 ^ 2 = 4 mal, was, wenn auf Ganzzahlen gerundet, da die Elemente einen ganzzahligen Wert ergeben, 3,33 = 4. Wir versuchen weiter, den Fehler bei der Verarbeitung eines Signals von 8 zu reduzieren. Elemente benötigen wir bereits 11 Triggerketten mit 8 Elementen. Ich nehme an, dass dies ein Mechanismus ist, mit dem Sie die Situation beurteilen und eine Entscheidung über die Änderung des Verhaltens eines biologischen Objekts treffen können. Meiner Meinung nach vernünftig und effizient genug. Und unter Berücksichtigung der Tatsache, dass wir über die Natur wissen, dass sie Ressourcen so sparsam wie möglich nutzt, ist die Hypothese gerechtfertigt, dass das biologische System diesen Mechanismus nutzt. Und wenn wir das neuronale Netzwerk trainieren, verringern wir tatsächlich die Fehlerwahrscheinlichkeit, da wir eine analytische Beziehung finden müssen, um den Fehler vollständig zu beseitigen.
Wir wenden uns der Analyse numerischer Daten zu. Bei der Analyse numerischer Daten versuchen wir, eine analytische Abhängigkeit in der Form y = f (xi) zu wählen. Und im ersten Stadium finden wir sie. Nachdem wir sie gefunden haben, können die vorhandenen Reihen relativ zur Regressionsgleichung als binär dargestellt werden, wobei wir positiven Werten 1 und negativen Werten 0 zuweisen. Anschließend analysieren wir eine Reihe identischer Elemente. Wir bestimmen die größte Verteilung kürzerer Ketten entlang der Kettenlänge.
Als nächstes wenden wir uns dem Erdos-Renyi-Theorem zu. Daraus folgt, dass bei der Durchführung einer großen Anzahl von Tests eines Zufallswerts eine Kette identischer Elemente in allen Registern der erzeugten Zahl gebildet werden muss, dh m = log2N. Wenn wir nun die Daten untersuchen, wissen wir nicht, wie groß das Volumen der Serie wirklich ist. Wenn Sie jedoch zurückblicken, gibt uns diese maximale Kette Anlass zu der Annahme, dass R ein Parameter ist, der ein Feld von Zufallsvariablen charakterisiert (Abbildung 19).
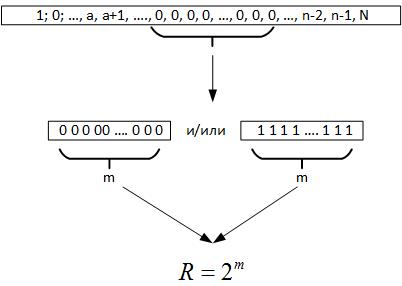
Abb. 19.
Das heißt, wenn wir R und N vergleichen, können wir mehrere Schlussfolgerungen ziehen:
- Wenn R <N ist, wird der Zufallsprozess für historische Daten mehrmals wiederholt.
- Wenn R> N ist, hat der Zufallsprozess eine Dimension, die höher als die verfügbaren Daten ist, oder wir haben die Gleichung der Zielfunktion falsch bestimmt.
Dann entwerfen wir für den ersten Fall ein neuronales Netzwerk mit 2 ^ m-Sensoren. Ich nehme an, wir können ein Paar Sensoren hinzufügen, um die Übergänge zu erfassen, und wir trainieren dieses Netzwerk anhand historischer Daten. Wenn das Netzwerk aufgrund von Schulungen nicht lernen kann und mit einer Wahrscheinlichkeit von 50% das richtige Ergebnis liefert, bedeutet dies, dass die gefundene Zielfunktion optimal ist und nicht verbessert werden kann. Wenn das Netzwerk lernen kann, werden wir die analytische Abhängigkeit weiter verbessern.
Wenn die Dimension der Reihe größer als die Dimension einer Zufallsvariablen ist, kann die Fraktalitätseigenschaft der Zufallsvariablen verwendet werden, da jede Reihe der Größe m alle Teilräume niedrigerer Dimensionen enthält. Ich nehme an, dass es in diesem Fall sinnvoll ist, das neuronale Netzwerk auf alle Daten außer den Ketten m zu trainieren.
Ein anderer Ansatz für den Entwurf neuronaler Netze kann der Prognosezeitraum sein.
Zusammenfassend muss gesagt werden, dass auf dem Weg zu dieser Veröffentlichung viele Aspekte entdeckt wurden, bei denen sich die Größe der Dimension einer Zufallsvariablen und ihre entdeckten Eigenschaften mit anderen Aufgaben bei der Analyse der Daten überschnitten. Aber im Moment ist dies alles in einer sehr rohen Form und wird für zukünftige Veröffentlichungen übrig bleiben.
Vorheriger Teil:
Teil 1 ,
Teil 2