Posit-Arithmetik: Besiegt einen Gleitkomma in seinem eigenen Feld. Teil 2

Teil 1

4. Quantitativer Vergleich numerischer Systeme

4.1. Dezimalgenauigkeit

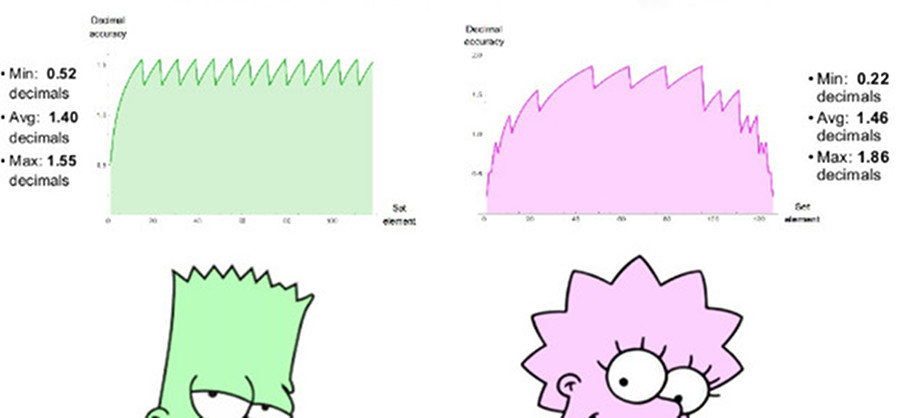
Genauigkeit ist das Gegenteil von Fehler. Wenn wir ein Paar von Zahlen x und y (ungleich Null und ein Vorzeichen) haben, beträgt der Abstand zwischen ihnen in Größenordnungen $$$\ mid log_ {10} (x / y) \ mid$ Dezimalordnungen, dies ist das gleiche Maß, das den Dynamikbereich zwischen den kleinsten und größten darstellbaren positiven Zahlen x und y definiert. Die ideale Verteilung von zehn Zahlen zwischen 1 und 10 in einem reellen Zahlensystem wäre keine gleichmäßige Verteilung von Zahlen in der Reihenfolge von 1 bis 10, sondern exponentiell: $$$1, 10 ^ {1/10}, 10 ^ {2/10}, ..., 10 ^ {9/10}, 10$ . Dies ist die Dezibel-Skala, die Ingenieure seit langem verwenden, um Beziehungen auszudrücken. Beispielsweise sind 10 Dezibel ein zehnfaches Verhältnis. 30db bedeutet Koeffizient $$$10 ^ 3 = 1000$ . Das 1-dB-Verhältnis ist ein Faktor von ungefähr 1,26. Wenn Sie den Wert mit einer Genauigkeit von 1 dB kennen, haben Sie eine Genauigkeit von 1 Dezimalstelle. Wenn Sie den Wert mit einer Genauigkeit von 0,1 dB kennen, bedeutet dies 2 Zeichen Genauigkeit usw. Die Dezimalgenauigkeitsformel lautet $$$log_ {10} (1 / \ mid log_ {10} (x / y) \ mid) = - log_ {10} (\ mid log_ {10} (x / y) \ mid)$ Dabei sind x und y entweder gültige Werte, die mit Rundungssystemen berechnet wurden, z. B. in Float- und Posit-Formaten, oder Ober- und Untergrenzen, wenn strenge Systeme mit Intervallen verwendet werden, oder gültige Werte.

4.2. Definieren von Float- und Posit-Vergleichssätzen

Wir können maßstabsgetreue Modelle von Float- und Posit-Zahlen mit einer Länge von jeweils 8 Bit erstellen. Der Vorteil dieses Ansatzes besteht darin, dass 256 Werte klein genug sind, damit wir sie vollständig testen und alles vergleichen können $$$256 ^ 2$ Vorkommen in Tabellen für Additions-, Subtraktions-, Multiplikations- und Divisionsoperationen. Reelle Zahlen mit einer Genauigkeit von 1/4 haben ein Vorzeichenbit, vier Bits des Exponenten und drei Bits des Bruchteils und entsprechen allen Regeln des IEEE 754. Die kleinste positive Zahl (denormalisiert) ist 1/1024, die größte positive Zahl ist 240, der Dynamikbereich ist asymmetrisch und gleich 5.1 Dezimalstellen. 14-Bit-Kombinationen stehen für NaN.

Eine vergleichbare 8-Bit-Position verwendet es = 1 und hat einen Bereich positiver Zahlen von 1/4096 bis 4096, einen symmetrischen Dynamikbereich von 7,2 Dezimalstellen. Es gibt keine NaN-Werte. Wir können in beiden Sätzen Diagramme mit dezimaler Genauigkeit positiver Zahlen zeichnen, wie in Abb. 2 gezeigt. 7. Beachten Sie, dass die durch Positivzahlen dargestellten Werte einen um zwei Dezimalstellen größeren Dynamikbereich aufweisen als Gleitkommazahlen, und dass die Genauigkeit für alle Werte gleich oder größer ist, mit Ausnahme derjenigen, bei denen Gleitkommazahlen nahe am Überlauf oder am Überlauf liegen. Die Einrückung der Graphen für beide Systeme ist eine logarithmische Approximation einer stückweise linearen Funktion. Bei Gleitkommazahlen nimmt die Genauigkeit nur links ab, im Bereich nahe der Antipersonität, rechts bricht die Funktion ab, weil dann kommen die Werte von NaN. Die Posit-Zahlen haben eine symmetrischere Funktion mit abnehmender Genauigkeit an den Kanten.


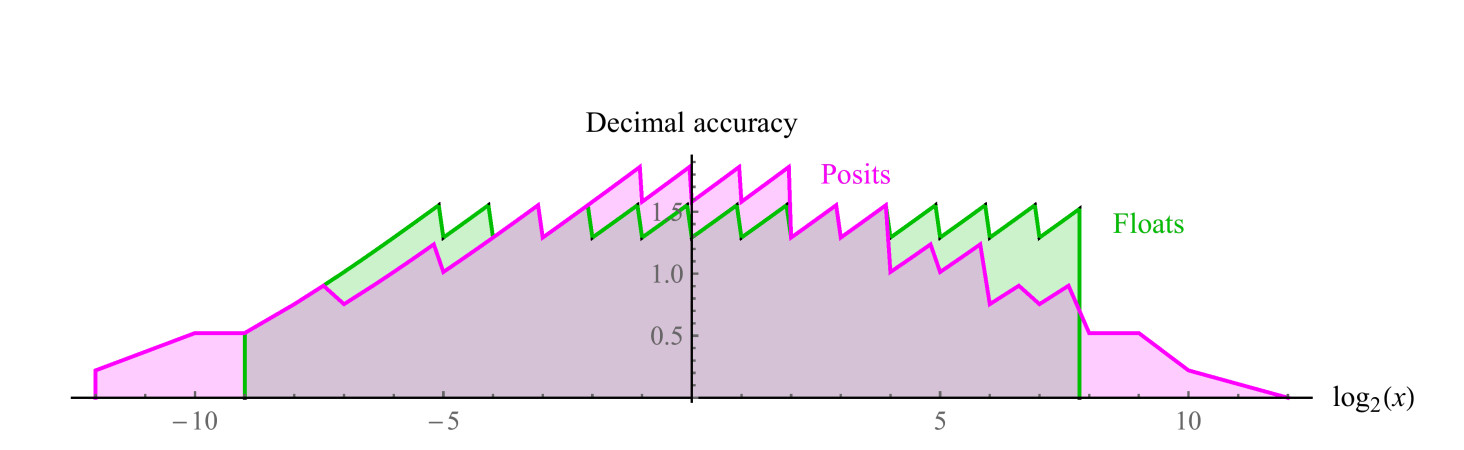
Abb. 7. Vergleich der Dezimalgenauigkeit von Float- und Posit-Zahlen

4.3. Vergleichen von Operationen mit einzelnen Argumenten

4.3.1. Inverser Wert

Für jeden möglichen Eingabe-x-Wert der 1 / x-Funktion kann das Ergebnis genau einem anderen Wert in der angegebenen Menge entsprechen oder gerundet werden. In diesem Fall können wir den Dezimalfehler anhand der Formel aus Abschnitt 4.1 messen. Bei Gleitkommazahlen kann das Ergebnis zu einem Überlauf führen oder NaN. Siehe Abb. 8.



Abb. 8. Quantitativer Vergleich von Float- und Posit-Zahlen bei der Berechnung des inversen Werts

Die Kurven im rechten Diagramm zeigen die Größe des Fehlers bei der Berechnung des inversen Werts, während die Gleitkommazahlen zu NaN führen können. Posit-Zahlen sind in einer großen Anzahl von Fällen dem Float überlegen, und diese Überlegenheit bleibt im gesamten Bereich erhalten. Die Berechnung der Umkehrung der denormalisierten Float-Zahlen führt zu einem Überlauf, der zu einem unendlichen Fehlerwert führt, und natürlich gibt das NaN-Argument die Umkehrung der NaN an. Die Positivzahlen werden relativ zur inversen Wertberechnung geschlossen.

4.3.2. Quadratwurzel

Die Quadratwurzelfunktion führt nicht zu Überlauf oder Anti-Überlauf. Für negative Argumente und für NaN ist das Ergebnis NaN. Denken Sie daran, dass wir ein „Skalenmodell“ für Float- und Posit-Zahlen haben. Die Vorteile von Posit nehmen mit zunehmender Datengenauigkeit zu. Bei 64-Bit-Float- und Posit-Fehlern beträgt der Posit-Fehler etwa 1/30 des Float-Fehlers anstelle von 1/2.

4.3.3. Platz

Eine andere übliche unäre Operation ist $$$x ^ 2$ . Überläufe und Anti-Überläufe sind beim Quadrieren eines Schwimmers häufig. Für fast die Hälfte eines Floats führt das Quadrieren nicht zu einem aussagekräftigen Ergebnis, während das Quadrieren der Positivzahl immer zur Positivzahl führt (das Quadrat der vorzeichenlosen Unendlichkeit ist die vorzeichenlose Unendlichkeit).


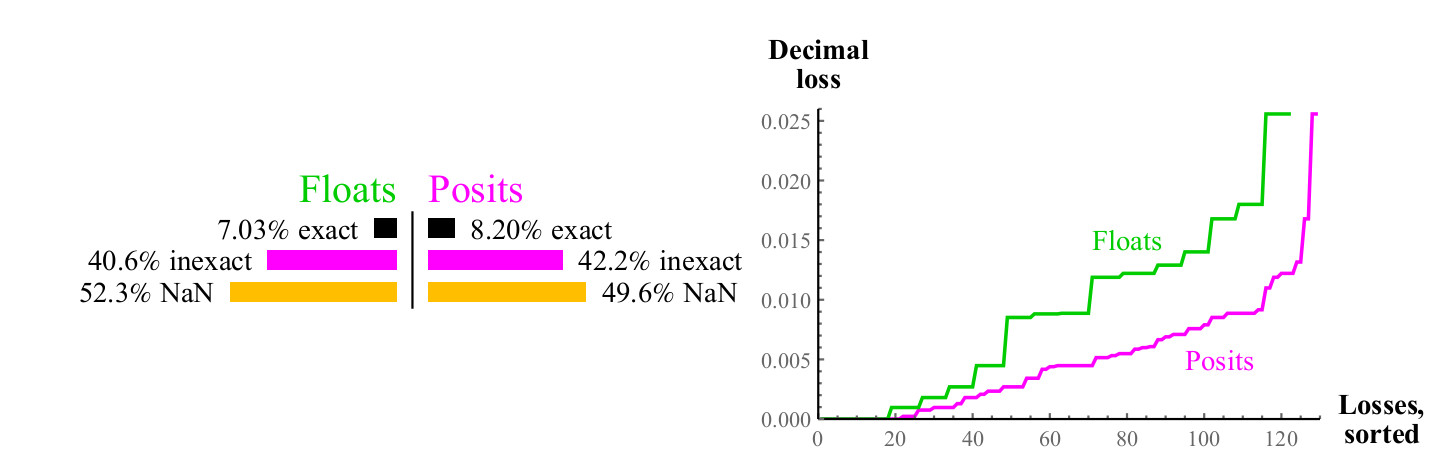
Abb. 9. Quantitativer Vergleich von Float- und Posit-Zahlen bei der Berechnung $$$\ sqrt x$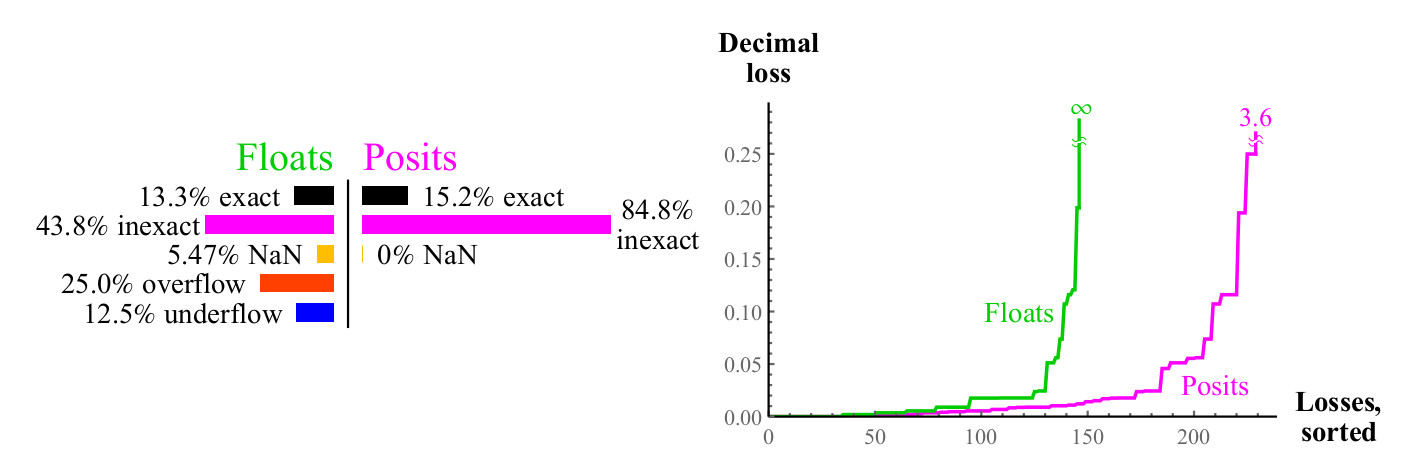


Abb. 10. Quantitativer Vergleich von Float- und Posit-Zahlen bei der Berechnung $$$x ^ 2$

4.3.4. Basis 2 Logarithmus

Wir haben auch einen Vergleich durchgeführt, um die Logarithmusfunktion der Basis 2 abzudecken, d. H. Den Prozentsatz der Fälle, in denen $$$log_2 (x)$ kann genau dargestellt werden, und wenn es nicht genau dargestellt werden kann, wie viele Dezimalstellen wir verlieren. Float-Zahlen haben in diesem Fall den einzigen Vorteil: Sie können zur Darstellung verwendet werden $$$log_2 (0)$ wie $$$- \ infty$ und $$$log_2 (\ infty)$ wie $$$\ infty$ Dies wird jedoch durch ein großes Wörterbuch mit ganzzahligen Zweierpotenzen für positive Zahlen mehr als ausgeglichen.


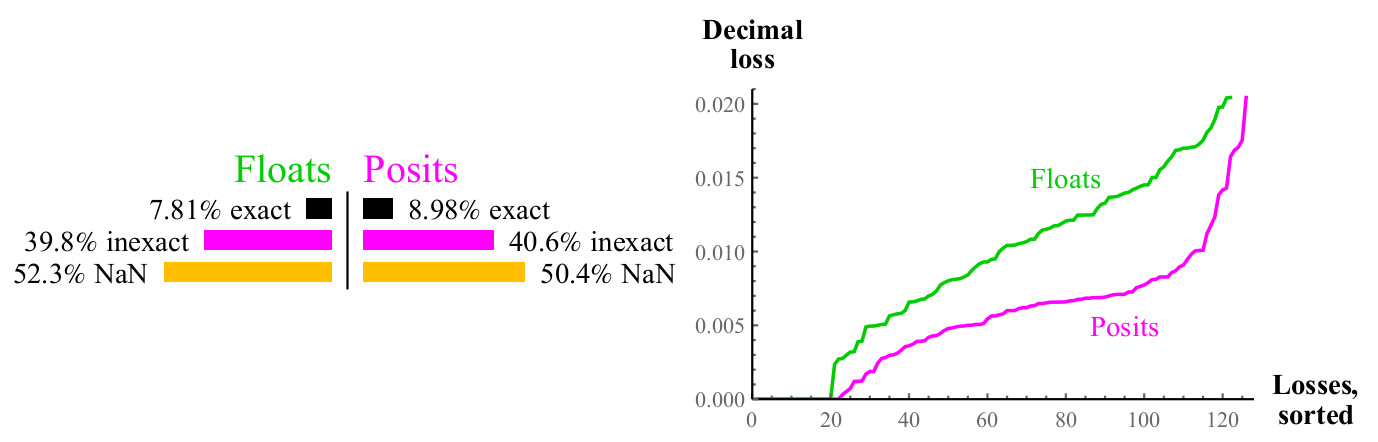
Abb. 11. Quantitativer Vergleich von Float- und Posit-Zahlen bei der Berechnung $$$log_2 (x)$

Der Graph ähnelt dem für die Quadratwurzel, etwa die Hälfte der Fälle ergibt in beiden Fällen NaN, aber Positivzahlen haben den halben Verlust an Dezimalgenauigkeit. Wenn Sie rechnen können $$$log_2 (x)$ müssen Sie nur das Ergebnis mit einem Skalierungsfaktor multiplizieren, um zu erhalten $$$ln (x)$ oder $$$log_ {10} (x)$ oder Logarithmus mit einem anderen Grund.

4.3.5. Aussteller $$$2 ^ x$

Ebenso, wenn Sie rechnen können $$$2 ^ x$ können Sie leicht den Skalierungsfaktor verwenden, um zu erhalten $$$e ^ x$ oder $$$10 ^ x$ usw. Posit-Nummern haben eine Ausnahme: $$$2 ^ x$ entspricht NaN, wenn das Argument ist $$$\ pm \ infty$ .


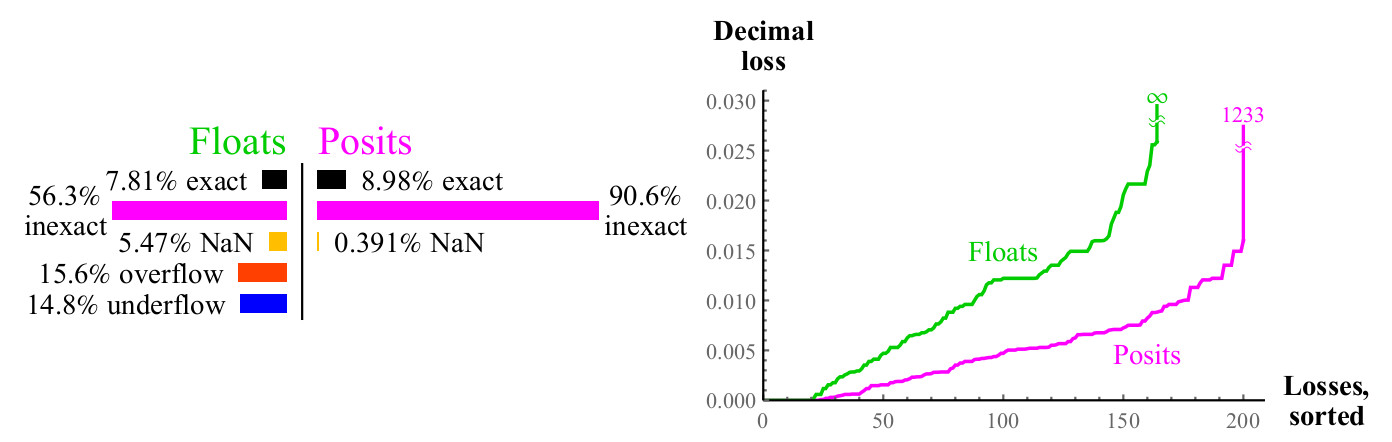
Abb. 12. Quantitativer Vergleich von Float- und Posit-Zahlen bei der Berechnung $$$2 ^ x$

Der maximale Dezimalverlust für Positivzahlen kann seitdem groß erscheinen $$$2 ^ {maxpos}$ wird auf maxpos abgerundet. In diesem Beispiel ist nur eine kleine Anzahl von Fehlern so groß wie $$$log_ {10} (24096) \ ca.1233$ Dezimalstellen. Entscheiden Sie, was besser ist: Verlieren Sie mehr als tausend Dezimalstellen oder verlieren Sie unendlich viele Dezimalstellen? Wenn Sie nicht so große Zahlen verwenden können, gewinnen positive Zahlen immer noch, da Fehler mit kleinen Werten viel besser sind. In allen Fällen, in denen Sie bei Verwendung von Positivzahlen eine große Anzahl von Dezimalstellen verlieren, geht das Eingabeargument weit über das hinaus, was Float-Zahlen überhaupt ausdrücken können . Die Grafiken zeigen, wie Positivzahlen in Bezug auf den Dynamikbereich, in dem das Ergebnis sinnvoll ist, stabiler sind und in diesem Bereich eine höhere Genauigkeit aufweisen.

Für gewöhnliche unäre Operationen $$$1 / x, \ sqrt x, x ^ 2, log_2 (x)$ und $$$2 ^ x$ Posit-Zahlen sind vollständig und ausnahmslos genauer als Float-Zahlen mit der gleichen Anzahl von Bits und liefern aussagekräftige Ergebnisse in einem weiten Dynamikbereich. Wir wenden uns nun vier elementaren arithmetischen Operationen zu, die zwei Argumente haben: Addition, Subtraktion, Multiplikation und Division.

4.4. Vergleichen der Operationen zweier Argumente

Wir können das Skalenmodell eines Zahlensystems verwenden, um die arithmetischen Operationen zweier Argumente wie Addition, Subtraktion, Multiplikation und Division zu untersuchen. Um 65536 Ergebnisse zu visualisieren, erstellen wir ein „Abdeckungsdiagramm“ von 256 * 256, das deutlich zeigt, welcher Anteil der Ergebnisse genau und ungenau ist, Überlauf, Überlauf oder NaN verursacht.

4.4.1. Addition und Subtraktion

Als $$$x - y = x + (- y)$ Funktioniert sowohl für Float als auch für Posit. Es ist nicht erforderlich, die Subtraktion separat zu untersuchen. Für die Additionsoperation berechnen wir den genauen Wert $$$z = x + y$ und vergleichen Sie es mit dem Betrag, der in jedem der Zahlensysteme zurückgegeben wird. Es kann vorkommen, dass das Ergebnis ungenau ist, dann muss es auf die nächste endliche Zahl ungleich Null gerundet werden, Überlauf oder Anti-Überlauf, oder es kann zu Unsicherheiten in der Form kommen $$$\ infty- \ infty$ was zu NaN führt. Jeder dieser Fälle ist farblich markiert, und wir können die gesamte Additionstabelle auf einen Blick abdecken. Beim Runden der Ergebnisse ändert sich die Farbe von Schwarz (exakter Wert) zu Lila (exakter Wert für Posit und Float). Abb. 13 zeigt, wie das Abdeckungsdiagramm für Float- und Unum-Zahlen aussieht. Wie bei unären Operationen, aber mit viel mehr Punkten, können wir Schlussfolgerungen über die Fähigkeit jedes Zahlensystems ziehen, aussagekräftige und genaue Antworten zu geben:


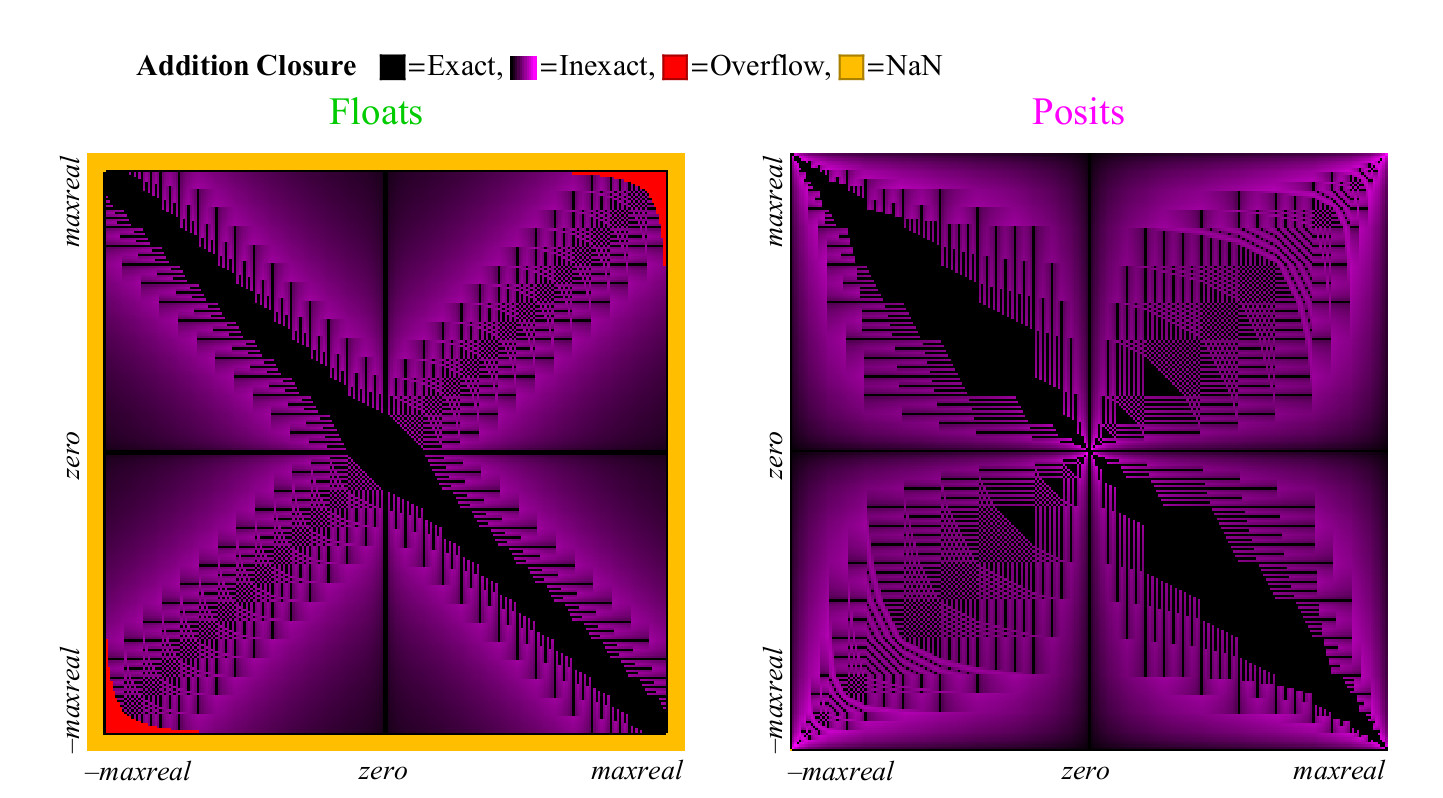
Abb. 13. Vollständiges Abdeckungsdiagramm zum Hinzufügen von Float- und Posit-Zahlen


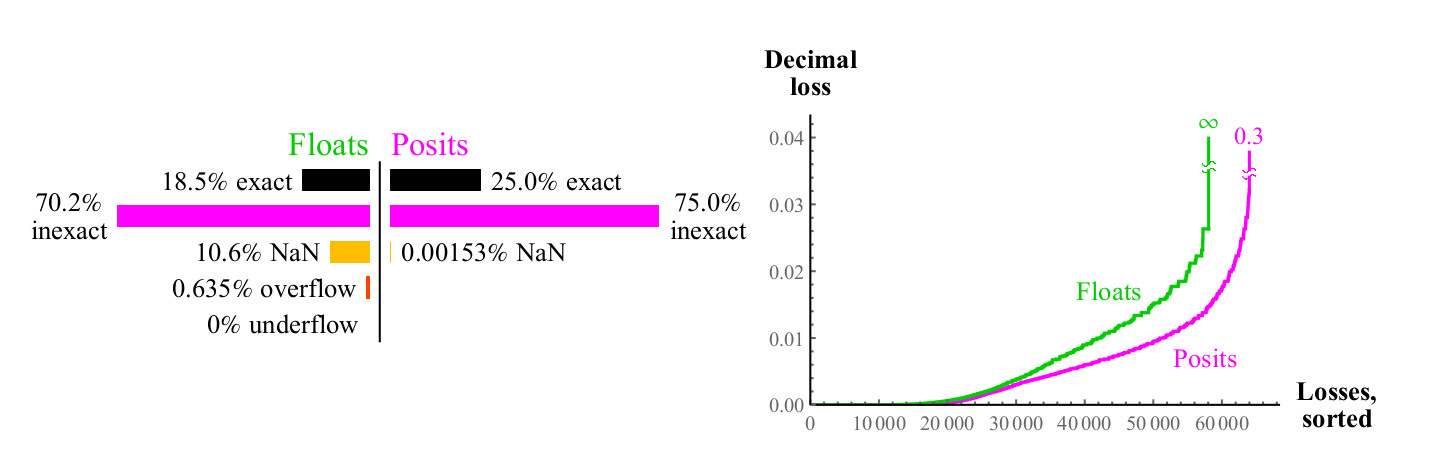
Abb. 14. Quantitativer Vergleich der Float- und Posit-Zahlen zur Addition

Auf den ersten Blick wird deutlich, dass die Position im Additionsdiagramm deutlich mehr Punkte enthält, bei denen das Ergebnis genau ist. Der breite schwarze diagonale Streifen im Abdeckungsdiagramm für Float ist viel breiter als für eine größere Genauigkeit, da er eine denormalisierte Zahlenzone darstellt, in der Float-Zahlen in gleichen Intervallen wie Festkommazahlen voneinander beabstandet sind. Solche Zahlen machen einen großen Anteil aus der Gesamtzahl nur bei 8-Bit-Zahlen.

4.4.2. Multiplikation

Wir verwenden einen ähnlichen Ansatz, um zu vergleichen, wie gut sich die Float- und Posit-Zahlen multiplizieren. Im Gegensatz zur Addition kann die Multiplikation einen Überlauf der Float-Zahlen verursachen. "Allmählicher Überlauf", die Zone, die Sie in der Mitte in Abb. 15 sehen können. nach links. ( bedeutet denormalisierte Zahlen. Ca. transl. ) Ohne diese Zone hätte die blaue Überlaufzone eine Rautenform. Das Multiplikationsdiagramm für Positivzahlen ist weniger farbenfroh, was besser ist. Nur zwei Pixel werden als NaN nahe der Stelle hervorgehoben, an der sich die Nullmarke der Achsen befindet (die Pixel befinden sich vertikal ganz links in der Mitte und horizontal in der Mitte unten. Ca. Transl. ). Es gibt Multiplikationsergebnisse $$$\ pm \ infty \ cdot 0 = NaN$ . Float-Nummern haben mehr Fälle, in denen das Produkt genau ist, aber zu einem schrecklichen Preis. Wie in Fig. 15 gezeigt, führt fast 1/4 aller Schwimmerprodukte entweder zu einem Überlauf oder zu einem Überlauf, und dieser Anteil nimmt mit zunehmender Schwimmergenauigkeit nicht ab.


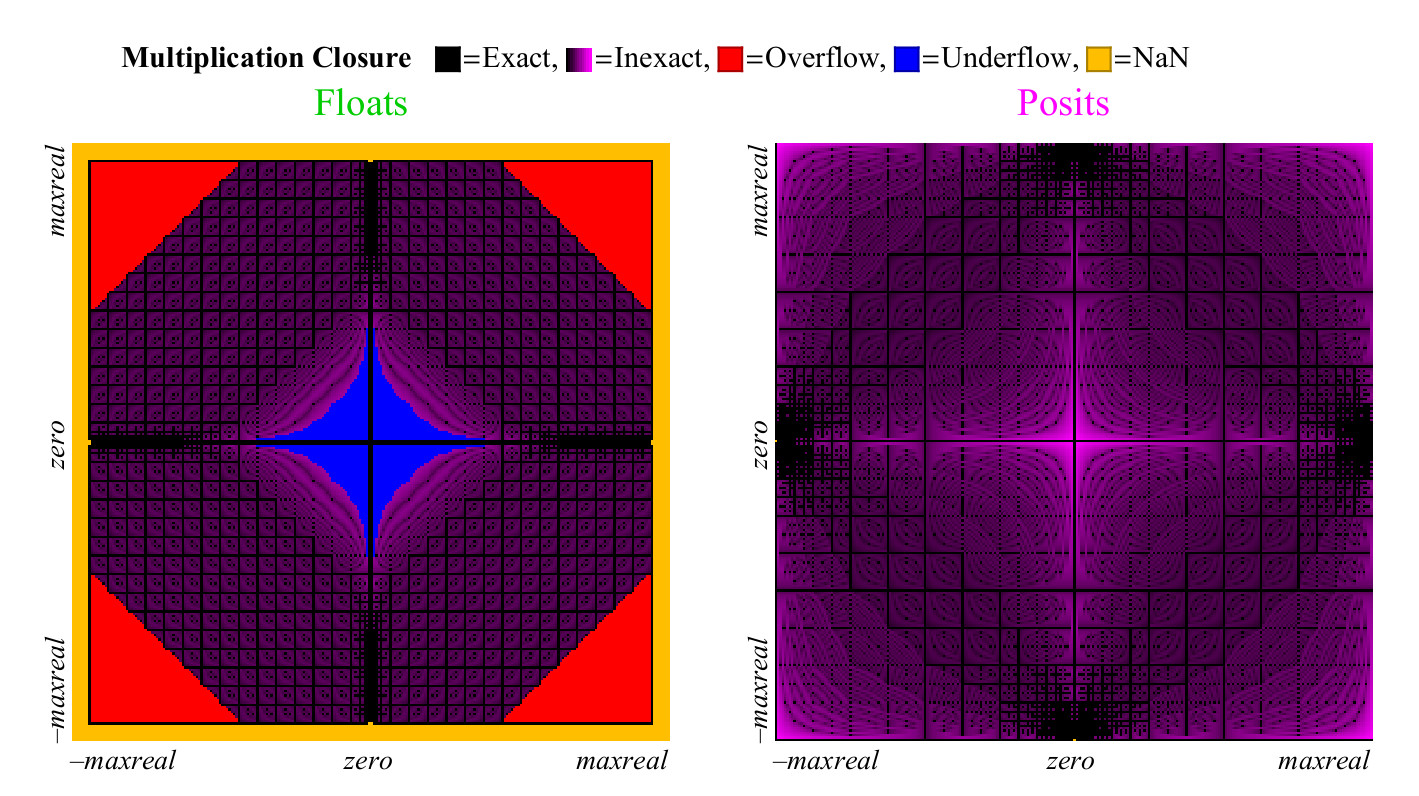
Abbildung 15. Diagramm zur vollständigen Abdeckung zum Multiplizieren von Float- und Posit-Zahlen

Der schlimmste Fall einer Rundung für Positivzahlen tritt auf, wenn $$$maxpos \ times maxpos$ das wird wieder auf maxpos gerundet. In solchen Fällen (sehr selten) beträgt der Fehler 3,6 Dezimalstellen. Wie die Grafik in Abb. 16, Posit-Zahlen sind deutlich besser als Float, minimieren Multiplikationsfehler.


Abb. 16. Quantitativer Vergleich von Float- und Posit-Zahlen zur Multiplikation

Das Abdeckungsdiagramm für die Divisionsoperation ähnelt dem Diagramm für die Multiplikation, aber die Zonen werden vertauscht, um Platz zu sparen. Es wird hier nicht angezeigt. Quantitative Indikatoren für die Division sind fast dieselben wie für die Multiplikation.

4.5. Vergleich von Float- und Posit-Zahlen zur Auswertung von Ausdrücken

4.5.1. Testen Sie das 32-Bit-Präzisionsbudget

Tests werden normalerweise auf der Grundlage der Mindestlaufzeit durchgeführt und geben oft kein vollständiges Bild davon, wie genau das Ergebnis ist. Eine andere Art von Test ist eine, bei der wir das Budget des Fehlers festlegen, dh die Anzahl der Bits pro Variable, und versuchen, als Ergebnis die maximale Dezimalgenauigkeit zu erhalten. Hier ist ein Beispiel für einen Ausdruck, mit dem wir numerische Systeme mit einem Budget von 32 Bit pro Zahl vergleichen können:

$$

$$X = \ left (\ dfrac {27/10-e} {\ pi - (\ sqrt 2+ \ sqrt 3)} \ right) ^ {67/16} = 302.8827196 \ dotsb$$

Die Regel ist, dass wir mit der besten Darstellung von Zahlen beginnen $$$\ pi$ und $$$e$ , möglich in jedem der numerischen Systeme und Darstellungen aller angegebenen ganzen Zahlen, und wir sehen, wie viele Dezimalstellen mit dem wahren Wert von X übereinstimmen, nachdem neun Operationen im Ausdruck ausgeführt wurden. Wir werden die falschen Zahlen in Orange hervorheben.

Trotz der Tatsache, dass 32-Bit-IEEE-Gleitkommazahlen eine Dezimalgenauigkeit haben, die von 7,3 bis 7,6 Dezimalordnungen reicht, ergibt die Akkumulation von Rundungsfehlern bei der Berechnung von X eine Antwort von 302. 912 , die nur drei gültige Ziffern hat. Dies ist einer der Gründe, warum Benutzer das Bedürfnis haben, überall 64-Bit-Float zu verwenden, da selbst bei einfachen Ausdrücken die Gefahr besteht, dass die Genauigkeit so stark verloren geht, dass das Ergebnis möglicherweise unbrauchbar wird.

32-Bit-Positivzahlen haben eine variable Dezimalgenauigkeit, die zwischen 8,2 und 8,5 Dezimalstellen für Zahlen mit einem Absolutwert von etwa 1 liegt. Bei der Berechnung von X erhalten wir eine Antwort von 302,882 31 , die doppelt so viele signifikante Stellen hat. Vergessen Sie auch nicht, dass 32-Bit-Posit-Zahlen einen Dynamikbereich von mehr als 144 Dezimalstellen haben und 32-Bit-Floats einen viel kleineren Dynamikbereich von 83 Bit haben. Daher wird die zusätzliche Genauigkeit des Ergebnisses nicht durch Verengung des Dynamikbereichs erreicht.

4.5.2. Vierfacher Test: Goldbergs Problem mit dem dünnen Dreieck

Es gibt ein klassisches „dünnes Dreieck“ -Problem [1]: Finden Sie die Fläche eines Dreiecks mit den Seiten a , b , c, wenn zwei der Seiten b und c nur 3 Einheiten der niedrigstwertigen Ziffer (Einheiten an der letzten Stelle, ULPs) sind, die länger als die Hälfte der Länge sind Seiten (Abb. 17).


Abb. 17. Goldbergs Problem mit dem dünnen Dreieck

Die klassische Formel für Fläche A verwendet die Zwischenvariable s:

$$

$$s = \ frac {a + b + c} 2; A = \ sqrt {s (s-a) (s-b) (s-c)}$$

Die Gefahr in dieser Formel besteht darin, dass s dem Wert von a und der Berechnung sehr nahe kommt $$$(s-a)$ erhöht den Rundungsfehler sehr. Versuchen wir es mit 128-Bit-IEEE-Gleitkommazahlen (mit vierfacher Genauigkeit) $$$a = 7, b = c = 7/2 + 3 \ mal 2 ^ {- 111}$ . (Wenn Sie das Lichtjahr als Maßeinheit nehmen, ist die kurze Seite nur 1/200 des Protonendurchmessers halb so lang wie die lange Seite. Dies macht jedoch ein Dreieck zur Höhe der Türöffnung oben.) Wir berechnen den Wert von A auch mit 128-Bit-Positivzahlen ( es = 7). Das Folgende sind die Ergebnisse:

$$$$ display $$ \ begin {matrix} \ textrm {True value:} & 3.14784204874900425235885265494550774498 \ dots \ times 10 ^ {- 16} \\ \ textrm {128-Bit IEEE float:} & 3. \ color {orange} { 63481490842332134725920516158057682788} \ dots \ times 10 ^ {- 16} \\ \ textrm {128-Bit-Posit:} & 3.147842048749004252358852654945507744 \ color {orange} {39} \ dots \ times 10 ^ {- 16} \ end {matrix} $$ $$ anzeigen

Positionsnummern haben eine Genauigkeit von bis zu 1,8 Dezimalstellen, die größer als die vierfache Genauigkeit sind und in einem weiten Dynamikbereich schweben: von $$$2 \ times 10 ^ {- 270}$ vorher $$$5 \ times 10 ^ {- 269}$ . Dies reicht aus, um die katastrophalen Folgen einer Erhöhung des Fehlers in diesem speziellen Fall zu vermeiden. Es ist auch interessant festzustellen, dass die Antwort im Posit-Format genauer ist als im Float-Format, selbst wenn wir sie am Ende in 16-Bit-Posit konvertieren.

4.5.3. Die Lösung der quadratischen Gleichung

Es gibt einen klassischen Trick, mit dem Rundungsfehler bei der Berechnung von Wurzeln vermieden werden sollen $$$r_1$ , $$$r_2$ Gleichungen $$$ax ^ 2 + bx + c = 0$ mit der üblichen Formel $$$r_1, r_2 = (- b \ pm \ sqrt {b ^ 2-4ac}) / (2a)$ wenn b viel größer als a und c ist , was zum Verschwinden der Ziffern auf der linken Seite führt, da $$$\ sqrt {b ^ 2-4ac}$ sehr nah an b . Aber anstatt Programmierer zu zwingen, sich mystische Tricks zu merken, ist es möglicherweise besser, die Berechnung mithilfe einer einfachen Formel aus einem Tutorial sicher zu machen. Put $$$a = 3, b = 100, c = 2$ und vergleichen Sie das Ergebnis im Format 32-Bit-Float und Posit.

Tabelle 5. Die Lösung der quadratischen Gleichung


Numerisch instabile Wurzel - $$$r_1$ Beachten Sie jedoch, dass 32-Bit-Posit 6 korrekte Ziffern anstelle von 4 für Float ergibt.

4.6. Vergleich von Schwimmern und Posit-Systemen für den klassischen LINPACK-Test

Die Hauptmethode zur Bewertung von Supercomputern war lange Zeit das Lösen $$$n \ times n$ lineare Gleichungssysteme $$$\ mathbf Axe = b$ . Der Test füllt nämlich die Matrix A mit Pseudozufallszahlen von 0 bis 1 und den Vektor b mit den Summen der Zeilen A. Dies bedeutet, dass die Lösung x ein Vektor ist, der aus Einheiten besteht. Der Test berechnet den Abzugssatz $$$\ | \ mathbf Axe-b \ |$ um die Richtigkeit zu überprüfen, obwohl es keine fest festgelegte Anzahl von Ziffern gibt, die in der Antwort wahr sein müssen. Ein typischer Verlust von mehreren Stellen Genauigkeit ist typisch für den Test, und normalerweise werden 64-Bit-Floats verwendet (nicht unbedingt IEEE). Anfänglich sah der Test n = 100 vor, aber diese Größe war für die schnellsten Supercomputer zu klein, so dass n auf 300, dann auf 1000 erhöht wurde und schließlich (vom Erstautor) der Test skalierbar wurde und die Anzahl der Operationen pro Sekunde angibt. basierend auf der Tatsache, dass der Test durchgeführt wird $$$\ frac {2} {3} n ^ 3 + 2n ^ 2$ Multiplikations- und Additionsoperationen.

Beim Vergleich von Posit und Float haben wir einen kleinen Nachteil des Tests festgestellt: Die Antwort im allgemeinen Fall ist keine Abfolge von Einheiten, da Rundungsfehler in den Summen in Zeilen auftreten. Ein solcher Fehler kann beseitigt werden, wenn wir herausfinden, wie Vorkommen in A 1 Bit beitragen, was außerhalb des Bereichs der möglichen Genauigkeit liegt, und dieses Bit auf 0 setzen. Dies gibt uns die Gewissheit, dass die Summe der Zeile A ohne Rundung darstellbar ist und die Antwort x ist ist eigentlich ein Vektor, der aus Einheiten besteht. Für die Originalversion der Aufgabe mit einer Größe von 100 x 100 gibt der 64-Bit-IEEE-Float eine Antwort dieser Art:

0,9999999999999 633626401873698341660201549530029296875
1.00000000000000 11102230246251565404236316680908203125
$$$\ vdots$
1.0000000000000 22648549702353193424642086029052734375

Keine der 100 Zahlen ist wahr;Sie sind nahe 1, aber niemals gleich 1. Mit positiven Zahlen können wir etwas Wunderbares tun. Mit 32-Bit-Posit-Zahlen und demselben Algorithmus berechnen wir den Rest$$r = A x - b unter Verwendung der Zusammenführungsoperation ist ein skalares Produkt. Dann entscheide dich$r = \mathbf Ax − b$$$A x ' = r (unter Verwendung von bereits verarbeitet$\mathbf Ax'=r$$$A ) und verwenden$\mathbf A$$$x ' zur Korrektur:$x'$$$$x \leftarrow x-x'$ . Das Ergebnis ist die beispiellos genaue Antwort auf den LINPACK-Test: $$$\{1, 1,...,1\}$ .Können LINPACK-Regeln die Verwendung eines neuen 32-Bit-Zahlentyps verbieten, dessen Verwendung es ermöglicht, ein perfektes Ergebnis mit einem Fehler von Null zu erzielen, oder weiterhin auf der Verwendung eines 64-Bit-Gleitkommas bestehen, das dies nicht zulässt? Diese Entscheidung wird von den Verantwortlichen für diesen Test getroffen. Für diejenigen, die lineare Gleichungssysteme lösen müssen, um echte Probleme zu lösen, anstatt die Geschwindigkeit von Supercomputern zu vergleichen, bietet posit erstaunliche Vorteile.

5. Fazit

Posit besiegt den Float in seinem eigenen Spiel: Mit ihm können Sie Berechnungen durchführen und Rundungsfehler reduzieren. Posit-Zahlen haben eine größere Genauigkeit, einen größeren Dynamikbereich und eine größere Abdeckung. Sie können verwendet werden, um bessere Ergebnisse zu erzielen als ein Float mit derselben Bittiefe oder (was ein noch größerer Wettbewerbsvorteil sein kann) dieselben Ergebnisse mit einer geringeren Bittiefe. Da die Systembandbreite begrenzt ist, bedeutet die Verwendung kleinerer Operanden eine schnellere Geschwindigkeit und einen geringeren Stromverbrauch.
Da sie als Float und nicht als Intervallsystem arbeiten, können sie als direkter Ersatz für Float betrachtet werden, wie hier gezeigt wurde. Wenn der Algorithmus, der float verwendet, die Tests besteht und die Zeit und Stabilität „gut genug“ sind, funktioniert er mit posit noch besser. Die in posit verfügbaren fusionierten Operationen bieten ein leistungsstarkes Tool, um die Anhäufung von Rundungsfehlern zu verhindern, und in einigen Fällen können Sie in Anwendungen, die eine hohe Leistung erfordern, sicher 32-Bit-Posit-Nummern anstelle von 64-Bit-Floats verwenden. Im Allgemeinen wird dadurch die Anwendungsleistung um das 2-4-fache gesteigert, der Stromverbrauch gesenkt, Energie gespart und die Kosten für die Datenspeicherung gesenkt. Die Hardware-Support-Position gibt uns das Äquivalent von ein oder zwei Schritten von Moores Gesetz.ohne dass die Größe des Transistors reduziert oder die Kosten erhöht werden müssen. Im Gegensatz zum Float bietet das Posit-System eine bitweise Reproduzierbarkeit der Ergebnisse auf verschiedenen Systemen, wodurch der Hauptnachteil des IEEE 754-Standards beseitigt wird. Die Posit-Nummern sind einfacher und eleganter als das Float und reduzieren die Anzahl der Geräte, die sie unterstützen. Obwohl Float-Zahlen mittlerweile allgegenwärtig sind, können Posit-Zahlen sie bald veralten lassen.

Referenzen:

1. David Goldberg. Was jeder Informatiker über Gleitkomma-Arithmetik wissen sollte.
ACM Computing Surveys (CSUR), 23 (1): 5–48, 1991. DOI: doi: 10.1145 / 103162.103163.
2. John L. Gustafson. Das Ende des Fehlers: Unum Computing, Band 24. CRC Press, 2015.
3. John L Gustafson. Jenseits des Gleitkommas: Computerarithmetik der nächsten Generation. Stanford-Seminar: https://www.youtube.com/watch?v=aP0Y1uAA-2Y , 2016. Die vollständige Transkription finden Sie
unter http://www.johngustafson.net/pdfs/DebateTranscription.pdf .
4. John L. Gustafson. Ein radikaler Ansatz zur Berechnung mit reellen Zahlen. Supercomputing
Frontiers and Innovations, 3 (2): 38–53, 2016. doi: http://dx.doi.org/10.14529/jsfi160203.
5. John L. Gustafson. Die große Debatte @ ARITH23. https://www.youtube.com/watch?v=
KEAKYDyUua4 , 2016. Die vollständige Transkription finden Sie unter http://www.johngustafson.net/pdfs/
DebateTranscription.pdf .
6. Ulrich W. Kulisch und Willard L. Miranker. Ein neuer Ansatz für wissenschaftliche Berechnungen, Band 7. Elsevier, 2014.
7. Weitere Websites. IEEE-Standard für Gleitkomma-Arithmetik. IEEE Computer Society, 2008.
DOI: 10.1109 / IEEESTD.2008.4610935.
8. Isaac Yonemoto. https://github.com/interplanetary-robot/SigmoidNumbers