So kam es, dass sich die Wissenschaft ungleichmäßig entwickelt, und daher gibt es in unserem heutigen Leben sozusagen einen Ort für Erfolge. Eine Leistung, natürlich wissenschaftlich, aber nicht weniger bedeutsam. Und jetzt, Leser, haben Sie die Möglichkeit, den Ort des Kunststücks, die offiziellen Preise für seine Zahlung (wie es in Ländern üblich ist, die sich selbst als zivilisiert bezeichnen) zu sehen und sogar Ihr Glück selbst zu versuchen. Nun, zur gleichen Zeit werden zumindest einige von Ihnen den Reiz spüren, Perlen in ganz gewöhnlichen Dingen zu finden.
Darüber hinaus wird in mehreren Serien eine Geschichte über die Dinge erzählt, die jedem Abiturienten (und sogar vielen Schulkindern) zugänglich sind. Es wird keine Beweise geben, da sie oft offensichtlich sind, und wenn sie hier präsentiert werden, würden sie nicht nur die Lautstärke erweitern, sondern auch viele Leser abschrecken.
Erste Serie
Zuerst gab es Sterne. Es gab einen Prozess, mit ihnen zu spielen, zu schauen und zu fühlen, sich zu werfen und einen leuchtenden Fallpfad zu beobachten. Die Sterne waren Muster. Und die Zahlen waren der Sandkasten. Die Zahlen drehten sich auf der neuen Seite und ein weiterer Stern erschien in den Lücken zwischen ihnen. Ihr Strahlen winkte und brannte am besten nicht, sondern ließ sich berühren, aufheben und winkte ihnen dann zu, um eine funkelnde Spur von Sternenstaub zu hinterlassen. Aber dann wurden die Sterne bekannt und es gab noch einen Job, um sie zu sortieren. Und dann kam eine Idee auf.
Die Idee war einfach - man kann damit Geld verdienen. Und ja, es hat wirklich motiviert. Aber es ist nicht zusammengewachsen. Es war unterhaltsam, es gab regelmäßige Sterne, die auf neue Weise leuchteten, es gab Vergnügen und es gab Fortschritte. Erst am Ende entstand ein Wald, ein durchgehender Wald aus leuchtenden Bäumen. Und ich war schwach, ich konnte diese Taiga nicht auf der Suche nach wahrem Licht sortieren, weil es Millionen von Bäumen gibt und ich allein bin. Daher schlage ich vor, dass Sie sich die Sterne ansehen und wenn sie interessant sind, können Sie 400.000 US-Dollar verdienen, aber die Wahrheit ist, dass es ein „Aber“ gibt - im Wald müssen Sie in der Lage sein, den richtigen Weg zu wählen.
Auf den Annäherungen an die Sterne
Was ist eine Nummer? Einerseits ist es ein Produkt unseres düsteren Geistes, das in der Natur nicht zu finden ist. Andererseits erlaubt uns eine solche Abstraktion, viele Prozesse zu modellieren, die wir alle in derselben Natur beobachten. Nur das Modell ist nicht gleich dem beobachteten Phänomen. Wir haben es also wieder mit der Anpassung an unsere bescheidenen Fähigkeiten zur Beschreibung der Natur zu tun. Ist das gut In Bezug auf die Genauigkeit ist die Beschreibung nicht sehr gut. Nicht weil jemand möglicherweise nicht genügend Dezimalstellen hat, sondern weil uns ein ungenau modelliertes Phänomen sehr überraschen kann, wenn sich herausstellt, dass dem Modell das eine oder andere spezifische Merkmal fehlt, das in der Realität vorhanden ist und manchmal sogar etwas nervig klingt unaufmerksame Naturforscher auf dem Kopf.
Lassen Sie uns vor diesem Hintergrund versuchen, die Vollständigkeit der Grundlage jeder Modellierung zu untersuchen - die Vollständigkeit des Verständnisses des Zahlenbegriffs. Nur eine Zahl, nur Wissen darüber, das anscheinend von früher Kindheit an festgelegt wurde - nun, was könnte es sonst sein? Aber genau dort können wir den Abgrund finden. Ja, derjenige, der keinen Boden hat und voller Sterne ist.
Es gibt keine Zahlen in der Natur. Aber in der Natur kann man die Beziehung sehen. Die Wolke ist größer (länger / breiter / dicker / wie Sie sonst werden) als die andere Wolke, was bedeutet, dass es einen Platz für Korrelation gibt. Das Verhältnis hat aber auch keine Zahlen. Es gibt nur zwei Wolken, eine mehr, die andere weniger, und es gibt ihr Verhältnis. Obwohl ja, wurde das Verhältnis auch vom Menschen erfunden. Daher kann man fragen - was nützt es? Der Vorteil ist folgender: Das Konzept der Korrelation ist dem Konzept der Zahl einen Schritt voraus. Zuerst gab es ein Verhältnis, und erst dann erschien eine Zahl. Genauer gesagt - Bruchzahlen. Wenn wir also die Beziehung verstehen, werden wir die Zahlen verstehen.
Wie werden Bruchzahlen erhalten? Sehr einfach - von der Notwendigkeit, die Korrelation zu modellieren. Zuerst gab es Verhältnisse von Stufen und Seiten des Landes, Schafe von einem Besitzer zu Schafen von einem anderen, das Gewicht einer Wassermelone zum Gewicht einer anderen. In all diesen Fällen bestand die Notwendigkeit, den Unterschied irgendwie auszudrücken. Der Unterschied wurde jedoch nicht streng durch die Anzahl der Stufen oder durch die Größe der benachbarten Wassermelone geteilt. Zuerst lernten sie, den Unterschied auszudrücken, indem sie sie in kleinere Maßeinheiten aufteilten (Ellbogen wurden zu den Schritten hinzugefügt und Finger wurden zu den Ellbogen hinzugefügt). Aber die Wissenschaft stand nicht still und forderte immer größere Genauigkeit. Infolgedessen waren sich alle einig über die Einheitlichkeit und vergaßen Finger, Ellbogen, Schritte und andere Pfunde mit Pfund Sterling. Die Einheitlichkeit wird in Zahlen ausgedrückt.
Wie korreliere ich zwei Segmente, wenn eines nicht ganzzahlig in das andere passt? Sie können mit Ihren Fingern messen, aber es ist genauer, ein kleineres Segment als Maßeinheit zu nehmen und es in identische Teile zu unterteilen. Mit diesen Teilen können Sie den Teil eines größeren Segments messen, der nicht vom gesamten kleineren Segment gemessen wird. Dann entsteht jedoch ein neuer Teil des größeren Segments, der von den ausgewählten Teilen nicht mehr messbar ist. Wir wenden eine Rekursion an und zerlegen die bereits defekten Teile erneut in noch kleinere Komponenten. Wir messen sie bisher unermesslich. Und wieder bekommen wir einen unermesslichen Rest. Teile erneut teilen, erneut messen. Wieder bekommen wir den Rest. Aber Sie können sich langweilen!
Infolgedessen kamen die Leute auf die Idee der Rundung und hörten auf, die Maßeinheit neu zu teilen. Das heißt, die Leute haben nach Genauigkeit bewertet (sie sagen, dass dies ausreichend ist). Aber die Natur vergibt keine Ungenauigkeiten bei der Modellierung.
Wie werden Verhältnisse heute modelliert? Sie werden unter Verwendung der Klassifizierung von Bruchzahlen modelliert. Die Klassifizierung lautet wie folgt: Es gibt ganze Zahlen und Bruchzahlen. Ganze sind immer noch instabil, aber gebrochene sind in endliche und unendliche Brüche unterteilt. Vorerst vergessen wir auch die letzten. Unendlich werden in rational und irrational unterteilt. Wir vergessen normalerweise den ersten Teil. Die irrationalen sind in algebraische und transzendentale unterteilt. Alles, keine Abteilungen mehr. Aus Gründen der Klarheit geben wir eine Klassifizierung in Form eines Bildes:
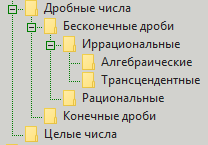
Warum ist diese Klassifizierung schlecht? Sie ist nicht so schlecht. Sie ist, wie Winnie the Pooh sagte, gut, aber irgendwie lahm ... Das heißt, es ist klar, dass es ihr mit der Genauigkeit des Ausdrucks von Werten wegen der Unendlichkeit nicht gut geht. Aber die Münze hat eine andere Seite. Diese Seite (in diesem Zusammenhang) wird als „Teilbarkeit“ bezeichnet. Wir können zwei Zahlen nicht genau voneinander trennen, weil wir uns gegen die Unendlichkeit ausruhen. Andererseits interessieren uns Phänomene aus der Welt der Zahlen wie Einfachheit und die Anzahl der Teiler, die die Unendlichkeit beseitigen, wenn sie auftreten. Primzahlen bilden die Basis der Zahlenreihe von ganzen Zahlen. Und diese wichtigen Zahlen (einschließlich zum Beispiel für den Komfort bei der Fernbezahlung von Dienstleistungen) hängen sehr stark von der Teilungsoperation ab. Und Teilung gibt uns oft Bruchteile. Und Brüche geben uns Bruchzahlen. Nun, für gebrochene Zahlen gab uns jemand die zuvor gegebene Klassifikation von endlich, unendlich, rational, irrational, algebraisch und transzendent. Aber gibt uns diese Klassifizierung die Möglichkeit, Antworten auf Fragen zu Zahlen zu finden? Zum Beispiel über die gleichen einfachen? Oder gebrochen? Es scheint zu geben, aber nicht so viel, wie wir möchten.
Nehmen Sie Primzahlen. Heute wird im Wesentlichen nach den maximalen Primzahlen gesucht. Das heißt, sie nehmen die Kandidatennummer und prüfen dann, ob es einfach ist oder nicht. Kandidaten erhalten einfach Zahlen - wenn Sie die Methode zur Überprüfung der Einfachheit für eine bestimmte Klasse von Zahlen kennen, dann ist hier die Liste der Kandidaten in Form von Vertretern der Klasse, die sie dumm hintereinander stellen und jede Zahl überprüfen, natürlich beginnend mit kleinen Werten. Und bis jetzt haben sie Zahlen in der Größenordnung von zwei bis zu achtzig Millionen erreicht. Dies ist eine Zahl von fast fünfundzwanzig Millionen Dezimalstellen. Im Prinzip sieht es beeindruckend aus. Aber was hindert uns daran, uns an den Slogan „höher, weiter, schneller“ zu erinnern?
Grundsätzlich werden wir durch mangelndes Verständnis behindert. Ja, unser Modell des Phänomens „Zahl“ ist unvollständig. Und ja, der Teil des Modells, der "Teilung" genannt wird, ist größtenteils unvollständig. Daher sind achtzig Millionen Einheiten im Computerspeicher die Grenze für die Menschheit. Warum Einheiten? Weil es wie die größten Primzahlen aussieht. Dies sind eine Einheit, jedoch in binärer Notation. Für sie gibt es den Luc-Lemer-Test, der uns eine einfache Zahl oder eine Verbindung zeigt. Und dieser Test erfordert jahrelange Arbeit eines Prozessorkerns, um eine Kandidatenzahl von achtzig Millionen Binäreinheiten zu überprüfen. Nur achtzig Megabyte oder zehn Megabyte, und die Menschheit kann nicht mehr weiter gehen. Was sind zehn Megabyte? Das ist ein Penny, das ist eine Kleinigkeit, es ist fast nichts für moderne Computer. Aber der Test läuft schon seit Jahren. Daher müssen Sie es auf Millionen von Computern ausführen, auf denen Freiwillige das entsprechende Programm installieren, und daher eine Kandidatennummer für eine bestimmte Anzahl von Sekunden überprüfen (und dies, wenn es viele Freiwillige gibt). Das Problem ist jedoch, dass es viele Kandidatenzahlen gibt und es daher viele Monate dauert, bis die nächste Primzahl gefunden ist. Und mit solchen Überlegungen kann man erwarten, dass die Bewegung von nur bis zu Hunderten Millionen binären Einheiten zehn Jahre dauern wird.
Ist es möglich, den Prozess zu beschleunigen? Du kannst. Es ist jedoch mehr Verständnis erforderlich. Zum Beispiel - wie kann man die Zeit zum Testen jeder Nummer verkürzen? Bisher wird eine solche Abnahme durch Massieren von Eisen erreicht. Oder die zweite Option - Sie können einen schnelleren Test der Einfachheit anbieten. Aber damit hat sich seit etwa 100 Jahren wenig geändert. Und doch, wenn Sie es herausfinden, dann wird es vielleicht mit uns klappen. Muss nur von Grund auf verstehen.
Sterne in der Nähe
Wenn man über die Beziehungen nachdenkt, kann jeder viel zur Wissenschaft beitragen. Nur neugierig zu sein ist genug. Man kann sich zum Beispiel fragen, warum die Klassifizierung von Bruchzahlen so ist. Und finden Sie die Antwort in einem Gedankenexperiment, um das Verhältnis derselben Segmente zu messen. Erstens werden die Segmente als 1 zu 2 korreliert. Dieses Verhältnis ist verständlich, es gibt uns die Zahl 2, die zeigt, wie oft das größere Segment das kleinere überschreitet. Und jetzt verlängern wir ein etwas kleineres Segment. Was wird passieren? Das Verhältnis wird nicht mehr ganz sein. Der durch die Verlängerung erzielte Überschuss hindert uns daran, eine einfache Antwort auf das Problem zu erhalten. Aber wir können es als Lineal verwenden. Wenn es eine ganze Zahl in ein halbes größeres Segment passt, können wir das Verhältnis durch diese ganze Zahl ausdrücken. Also bekommen wir das Verhältnis:
Dabei ist N die Häufigkeit, mit der der Überschuss aus dem Strecken der kleineren Länge in die Hälfte der größeren Länge angepasst wird. Also haben wir eine rationale Zahl. Es ist immer durch das Verhältnis der ganzen Zahlen gegeben. Wenn wir jetzt das kleinere Segment etwas länger verlängern, können wir eine Situation bekommen, in der wir, egal wie viel wir das kleinere Segment mit einer bestimmten ganzen Zahl multiplizieren, keine exakte Übereinstimmung mit einer bestimmten Anzahl von Längen des größeren Segments erhalten können. Wir haben also eine irrationale Zahl erhalten, die das neue Verhältnis kennzeichnet. Es ist zu beachten, dass eine mikroskopische Verschiebung der Segmentgrenze zu einem endlosen Prozess der Identifizierung des Längenverhältnisses führt. Ein Schritt für den bescheidenen Forscher und eine große Veränderung für die Zahlentheorie - ein neues Element in der Klassifikation ist erforderlich. Ein Schritt und - von der Mikrogröße bis zur Unendlichkeit. Von einer Kategorie von Zahlen zu einer völlig neuen, die grundsätzlich nicht mit der vorherigen kompatibel ist. Ist das nicht ein Stern?
Tatsächlich haben wir jedoch nur ein Segment geringfügig geändert. Woher kam also die grundlegend neue Kategorie? Im Allgemeinen ist die Klassifizierung wichtig, damit sie genau der Realität entspricht. Aber welche Genauigkeit ging mit irrationalen Zahlen einher? Mit ihnen können Sie jedes Verhältnis modellieren und nicht nur das Verhältnis von ganzen Zahlen. Daher ist es wirklich sinnvoll, solche Klassen zu trennen. Aber das ist nicht alles Genauigkeit, denn ich möchte all diese Unendlichkeiten verstehen, wie sie erscheinen, was sie bedeuten und warum sie überhaupt existieren. Zwar ist bei Unendlichkeiten nicht alles einfach, aber wir werden uns vorerst mit endlichen Beziehungen befassen. Es scheint, dass bei ihnen alles einfach ist, nimm N, dividiere es durch M und erhalte eine Bruchzahl. Es ist sehr gut, wenn sich die Zahl als kurz herausstellt, zum Beispiel 2,5 oder 3,25. Aber häufiger zur Welt sind Beziehungen der Form 4.12 (3456), dh wieder mit Unendlichkeiten, aber dies sind Unendlichkeiten „in der Periode“. Wenn Sie nur die wiederholten Zahlen bemerken, können Sie sehr einfach und kompakt eine Zahl aus einer unendlichen Anzahl von Zeichen aufzeichnen. So sind wir bekanntermaßen mit der Unendlichkeit umgegangen. Auch ein kleines Sternchen. Dies ist jedoch nur ein flüchtiger Blick.
Lassen Sie uns jetzt die Neugier einschalten und Fragen stellen. Und warum sind einige Bruchzahlen endlich und andere unendlich? Und warum sind einige Arten von unendlich unendlich lang, während andere mit einer Periode? Und warum sehen wir vor dem Punkt in Nummer 4.12 (3456) die Nummern 1 und 2? Und warum gibt es eine Vorperiode? Und warum sehen wir in dieser Zeit die Zahlen 3 und 4? Und warum ist die Periodenlänge in diesem Beispiel gleich vier? Und warum ist die Anzahl der Zahlen vor dem Zeitraum gleich zwei? Und wir werfen nur oberflächlich einen neugierigen Blick auf nur eine Bruchzahl. Und für andere Zahlen werden die Fragen noch interessanter sein.
Versuchen wir zu antworten. Warum sind Bruchzahlen endlich? Sehr einfach - in der Tat ist dies eine "optische Täuschung". Genauer gesagt - wir haben einen Trick angewendet. Um zum Beispiel die Zahl 2,5 zu erhalten, können Sie 5 durch 2 teilen. Und dafür haben wir alle in der Schule die Methode zum Teilen der "Ecke" gelehrt. Aber schauen wir uns diese Methode genauer an. Und dann stellen wir fest, dass der Fakir wie folgt wirkt: Er multipliziert die Dividende mit einer Konstante, die den Divisor oder seine Faktoren enthält. Und dann reduziert es genau die Faktoren von der Konstanten auf die Faktoren des Divisors. Es sieht so aus:
Das sind alles Wunder - eine Zwei von einem Teiler wird zu einer Zwei von einer Konstanten reduziert
das ist gleich
und eine fünf blieb als Ergebnis, die nach dem Dezimaltrennzeichen geschrieben wird. Die Nummer ist
nie geteilt
multipliziert es mit
von der Menge
. Aber wir sehen es nicht, dank der „optischen Täuschung“, die wir von der Schule aus trainiert haben, um während jeder Abteilungsabteilung unabhängig zu schaffen. Ist das nicht ein Star? Man musste nur das Laub über die gedämpften Darstellungen aus der Zeit der Grundschule schieben, als wir das Licht von etwas Neuem sahen, nicht ganz Gewöhnlichem, das nicht in der Schule unterrichtet wird (aber vergebens).
Lassen Sie uns nun die „optische Täuschung“ auf einer etwas höheren Ebene erklären. Wir haben das Teilungsergebnis einfach in ein Format übersetzt, das für die Speicherung und Wahrnehmung geeignet ist. Die Nummer selbst hängt nicht vom Format ab. Und die Anzahl der Zeichen darin ist auch. Wir haben bereits die Möglichkeit gesehen, Klammern um eine Periode zu setzen und dadurch die Unendlichkeit auf die Länge der Periode und zwei Klammern zu reduzieren. Dies ist ebenfalls ein Datenformat, das jedoch für periodische Brüche verwendet wird. Und das Format endlicher Brüche verbirgt die Unendlichkeit, indem es um Faktoren von der Basis des Dezimalzahlensystems reduziert wird. Wenn wir zum Beispiel das ternäre Zahlensystem nehmen, sieht die Division von 5 durch 2 folgendermaßen aus:
Das heißt, wir haben Unendlichkeit in Form einer periodischen Fraktion erhalten, weil wir jetzt eine andere Konstante verwendet haben, die keine Faktoren enthält, die mit der Zahl 2 reduziert werden können. In einem hexadezimalen System würde das Ergebnis jedoch wieder endgültig werden - 2.3. Aber die Nummer selbst bleibt irgendwo im Schatten, und die wahrscheinlich beste Aufzeichnung dafür wäre 5/2, und alles andere ist die Frage der Wahl des Präsentationsformats für diese Nummer.
Nun zu unendlichen Brüchen. Periodische werden durch Teilen von ganzen Zahlen erhalten, und irrationale (mit unendlicher Periodenlänge) werden durch Berechnen einer Wurzel von einem gewissen Grad aus einer ganzen Zahl erhalten. Das heißt, Menschen haben zwei Kategorien der Teilung aus der Abstraktion von ganzen Zahlen abgeleitet - mit unterschiedlichen Faktoren und mit denselben. Mit der ersten Option können Sie eine beliebige Ganzzahl in eine andere Ganzzahl unterteilen. Manchmal ergibt sich jedoch ein gebrochenes Ergebnis. Mit der zweiten Option können Sie die Zahlen nur in diejenigen unterteilen, die genau dem Ergebnis der Teilung entsprechen (einschließlich Mehrfach für Wurzeln mit hohem Grad). Im Allgemeinen haben wir die gleiche Aufteilung, jedoch ohne Einschränkung des Ergebnisses und mit der Einschränkung. Die Einschränkung führt uns zu zwei Optionen: Entweder reduzieren Sie den Divisor um einen Faktor aus der Dividende (und dann können Sie eine ganze Zahl erhalten, die dem Divisor entspricht) oder dividieren Sie die irreduzible Dividende durch eine bestimmte Zahl. Was kann dann eine "bestimmte Zahl" sein? Wenn es sich um eine Ganzzahl handelt, erhalten wir als Ergebnis einen Bruchteil (Dividende und Divisor sind nicht reduzierbar), der nicht einer Ganzzahl entspricht. Da Ganzzahlen nicht passen, müssen Sie daher nach einem Bruch suchen, der dem Ergebnis entspricht. Endliche Brüche verschwinden ebenfalls, weil sie tatsächlich eine Anzahl der Formen darstellen
was, wenn es mit sich selbst multipliziert wird, uns einen neuen Bruchteil der Form geben würde
Dies gibt uns wiederum einen endlichen oder periodischen Bruch und keine ganze Zahl. Daher ist es notwendig, einen Bruch auszuwählen, der das Verhältnis ihrer Quadrate zu einer ganzen Zahl mit einem unendlichen Wachstum von N und M verringert. Warum für unendliche ganze Zahlen das Verhältnis
kann ganz gemacht werden, aber nicht für das Ende? Denn je mehr Zahlen, desto weniger Einfluss hat ihre Diskretion auf das Ergebnis. Die ganze Zahl, die einer ausgewählten folgt, unterscheidet sich notwendigerweise um eins. Mit diesem Gerät können Sie das gewünschte Ergebnis nicht genau einstellen, da beispielsweise zwischen 1/1000 und 2/1000 unendlich viele Zahlen vorhanden sind, z. B. 11/10000 oder 145/100000 usw. Wenn die Länge der Zahl erhöht wird, ist es daher im Unendlichen möglich, jedes Ergebnis mit beliebiger Genauigkeit zu erhalten. Und dann multipliziere es mit sich selbst und erhalte eine ganze Zahl.
Gleichzeitig wird die Periode eines solchen Bruchteils wirklich unendlich, wie wir später sehen werden. Und eine unendliche Periode ist die Eigenschaft einer irrationalen Zahl, zu der wir von völlig rationalen Zahlen übergegangen sind. Hier ist so ein Sternenlicht, das sich sanft in die Dunkelheit der Unendlichkeit verwandelt.Aber warum brauchen wir diese Verbindung zwischen zwei Zahlenklassen? Vielleicht reicht einer? Versuchen wir zu simulieren. Wir haben also genau die Wurzel einer ganzen Zahl erhalten und zwei große ganze Zahlen gefunden, die zur Unendlichkeit tendieren und, wenn sie quadriert und voneinander geteilt werden, eine ganze Zahl ergeben. Fügen Sie nun eine dieser unendlich großen Zahlen hinzu. Was wird dann passieren? In unserer üblichen Sprache haben wir eine Definition für eine neue Zahl erhalten, die nicht periodisch ist (weil sie eine unendliche Periode hat) und gleichzeitig nicht die Wurzel des Ganzen ist. Das heißt, die neue Zahl passt nicht in die Klassifizierung, die uns aus rationalen und irrationalen Zahlen gegeben wurde. Und jetzt wurden alle diese Zahlen von Mathematikern transzendental genannt, weil man sie irgendwo platzieren muss. Aber ein interessanter Punkt - zuerst gab es Wurzeln von ganzen Zahlen, die als irrationale Zahlen bezeichnet wurden.und dann erschienen "andere" Zahlen. Das heißt, erstens wurde im Interesse der antiken griechischen Tradition die Überschätzung der Bedeutung von ganzen Zahlen genau auf der Grundlage von Methoden zur Gewinnung aus ganzen Zahlen klassifiziert. Die erste Methode war die Division und die daraus abgeleiteten rationalen Zahlen. Dann trafen sich die Menschen mit Wurzeln. Es gab also irrationale Zahlen. Und zusätzlich zum Rationalen und Irrationalen entstand eine dritte Kategorie. Darüber hinaus war die dritte Kategorie zunächst eine schreckliche Seltenheit, die Euler entdeckte, aber außer der Euler-Entdeckung gab es einfach keine anderen. Und es wurde beschlossen, das Irrationale in zwei Klassen zu unterteilen - algebraisch (dh von den Wurzeln her wachsend) und transzendent (speziell, herausragend, darüber hinaus, weil nur Euler sie finden konnte). Aber später wurden die Zahlen, die nicht von den Wurzeln kamen, massiv, und Mathematiker stellten sogar fest, dass es noch viel mehr gab,als algebraisch. Daher ist die Transzendenz (Merkmal) solcher Zahlen nur eine Hommage an die Tradition geworden. Wenn wir uns an das Konzept der Korrelation erinnern, werden all diese rationalen, irrationalen, algebraischen und transzendentalen Namen sofort zu künstlichen Namen für eine sehr bedingte Teilung von Zahlen, die sich aus einer einfachen Verschiebung des Endes eines der verglichenen Segmente ergibt. Nun, mit einem solchen Ansatz werden transzendentale Zahlen einfach „der Rest“, das heißt, wenn wir aus den Beziehungen der Segmente, um die Tradition des Extrahierens von ganzen Zahlen aufrechtzuerhalten, die Klassen auswählen, die durch die Operationen des Teilens und Extrahierens der Wurzel aus ganzen Zahlen erhalten werden, erhalten wir nur rational und algebraisch, aber alle der Rest ist transzendent. Das heißt, insgesamt gibt es nur drei Kategorien von unendlichen Brüchen. Daher wird der Name "transzendental" etwas angespannt,findest du nicht Okay, denn Tradition ist unser Alles, selbst in einer so exakten Wissenschaft wie der Mathematik.Das ist alles für jetzt. Lassen Sie uns in der nächsten Serie über rationale Sterne sprechen.