Wie man Polynome richtig färbt

Polynome sind nicht nur Übungen in abstrakten Angelegenheiten. Sie eignen sich hervorragend zum Erkennen von Strukturen an unerwarteten Orten.

Im Jahr 2015 half Jun Ho, ein ehemaliger Dichter, der Mathematiker wurde, das vor etwa 50 Jahren formulierte Problem zu lösen. Es wurde mit komplexen mathematischen Objekten, " Matroiden " und Graphen (Kombinationen von Punkten und Segmenten) assoziiert. Und es war auch mit Polynomen verbunden - Ausdrücken, die uns aus dem Mathematikunterricht bekannt sind und aus der Summe der Variablen bestehen, die in unterschiedlichem Maße angehoben wurden.

Irgendwann in der Schule haben Sie wahrscheinlich Klammern in Polynomen geöffnet. Sie können sich beispielsweise daran erinnern, dass x ² + 2xy + y ² = (x + y) ^{2 ist} . Ein praktischer algebraischer Trick, aber wo kann er nützlich sein? Es stellt sich heraus, dass Polynome perfekt dazu beitragen, verborgene Strukturen aufzudecken - und Ho hat diese Tatsache in seinem Beweis aktiv genutzt. Hier ist ein einfaches Rätsel, das dies veranschaulicht.

Angenommen, wir müssen zwei Spielerteams an einem quadratischen Tisch platzieren. Um Betrug zu verhindern, müssen Sie sicherstellen, dass die Spieler nicht neben anderen Spielern in ihrem Team sitzen. Wie viele Sitzmethoden gibt es?

Beginnen wir mit den Sitzplätzen des roten und blauen Teams. Angenommen, der rote Spieler sitzt oben in der Tabelle:



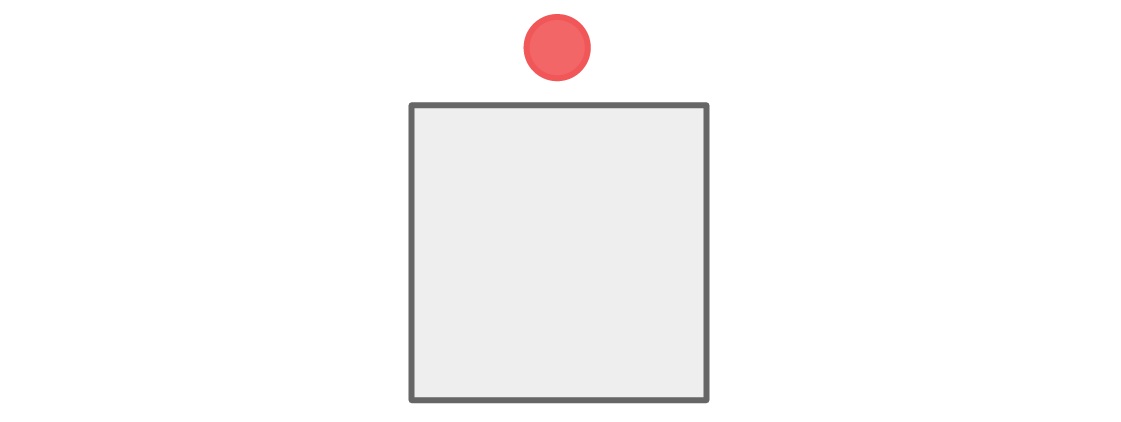
Es gibt zwei Plätze in der Nähe des obersten Platzes - rechts und links - und um die Regel zu erfüllen, müssen diese Plätze von blauen Spielern besetzt werden.



Das Feld darunter grenzt an die beiden blauen, daher muss der rote Spieler dort sitzen.



Keiner der Spieler sitzt neben einem Mitglied seines Teams und unsere Bedingung ist erfüllt.

Wir könnten auch mit dem blauen Spieler an der Spitze beginnen. Ähnliche Überlegungen führen zu folgender Anordnung:



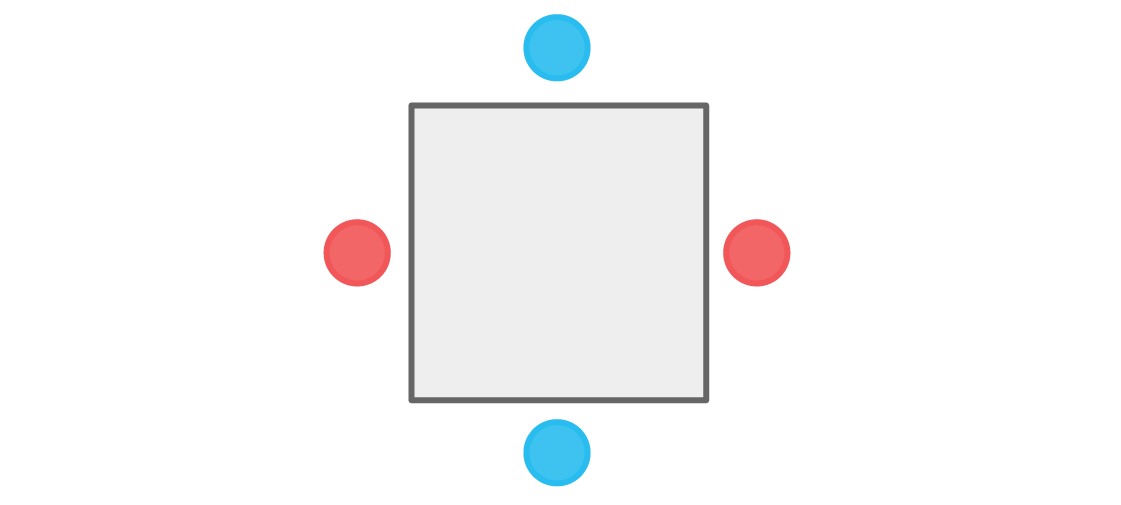
Auch hier sitzt kein Spieler neben anderen Mitgliedern seines Teams. Unsere Bedingung ist erfüllt und eine solche Sitzordnung ist akzeptabel. Tatsächlich gibt es genau zwei solche Sitzordnungen. Sobald wir die Farbe des oberen Punktes ausgewählt haben, sind alle anderen vollständig definiert.

Es gibt eine Möglichkeit herauszufinden, dass es nur zwei mögliche Sitzordnungen gibt, ohne alle diese Diagramme zu zeichnen. Beginnen wir von oben: Wir haben zwei Möglichkeiten, rot und blau. Nach dieser Auswahl bleibt eine Option (eine andere Farbe) für den linken und den rechten Sitz. Und für den unteren Sitz gibt es nur noch eine Option - die Farbe, mit der wir begonnen haben. Unter Verwendung des „Grundprinzips der Berechnung“ wissen wir, dass die Gesamtzahl der Opportunities das Ergebnis der Multiplikation der Anzahl der Opportunities für jede der Optionen ist. Dies ergibt 2 × 1 × 1 × 1 = 2 Sämlinge, wie wir aus unseren Diagrammen ermittelt haben.

Fügen Sie nun den dritten Befehl mit der dritten Farbe hinzu. Stellen Sie sich vor, wir haben rote, blaue und gelbe Spieler. Wie viele Sitzordnungen können getroffen werden, vorausgesetzt, die benachbarten Plätze müssen unterschiedliche Farben haben? Um alle Möglichkeiten abzubilden, müssen Sie einen ganzen Wagen mit Diagrammen zeichnen. Versuchen wir stattdessen, Berechnungen durchzuführen.

Für den Spitzenplatz haben wir jetzt die Wahl zwischen drei Farben. Nach dieser Auswahl können wir eine der beiden verbleibenden Farben für die linke und rechte Stelle auswählen.

Was wird unter dem Platz sein? Es besteht die Versuchung zu erklären, dass es für den letzten Sitz nur eine Option gibt, da er sich neben dem linken und dem rechten Sitz befindet. Aber fühlen Sie sich in dieser Logik fehlerhaft?



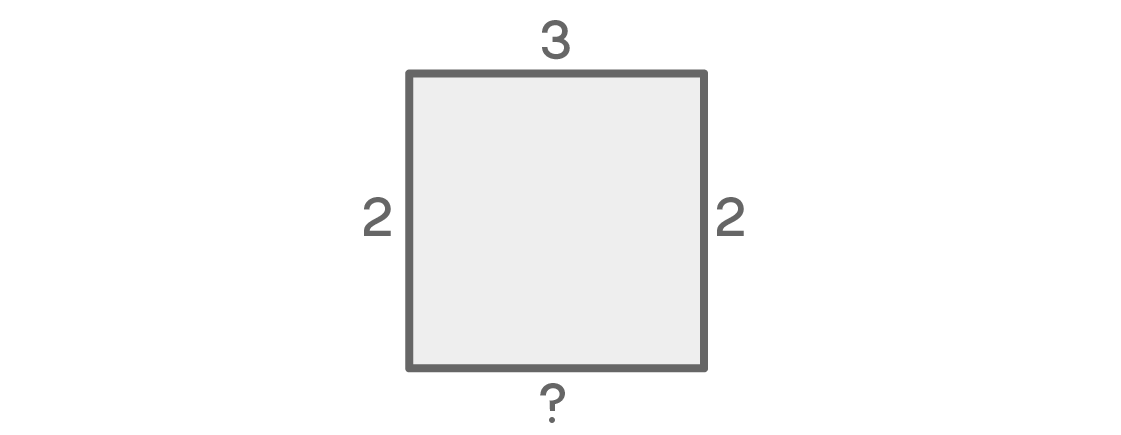
Wenn die linke und die rechte Stelle unterschiedliche Farben haben, gibt es für die unterste Stelle nur eine Option. Wenn es zum Beispiel links blau und rechts rot ist, muss der Boden gelb sein. Aber was ist, wenn die linke und die rechte Farbe gleich sind? In diesem Fall stehen für den unteren Platz zwei Optionen zur Auswahl. Diese letzte Wahl hängt von den vorherigen ab, was unsere Berechnungen erschwert.

Wir müssen zwei verschiedene Fälle betrachten: wenn die Farben links und rechts zusammenfallen und wenn sie sich unterscheiden.

Wenn die Farben links und rechts übereinstimmen, sieht die Anzahl der Möglichkeiten für jeden Ort folgendermaßen aus:



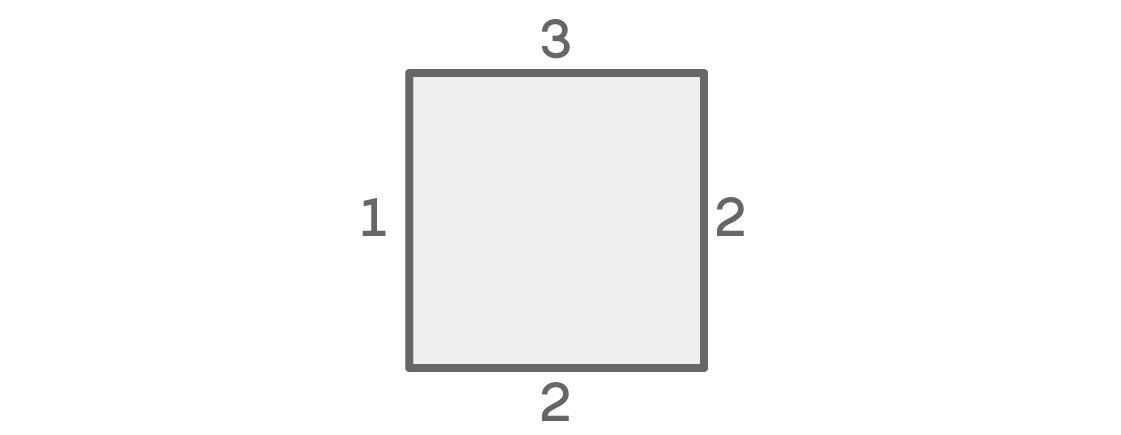
Für den oberen Sitz haben wir drei Möglichkeiten. Es gibt zwei links für rechts. Da wir davon ausgehen, dass die linke und die rechte Stelle dieselbe Farbe haben, haben wir nur eine Option für die linke Stelle: die gleiche Farbe wie die rechte. Da die Farbe links und rechts gleich ist, können wir eine der beiden verbleibenden Farben für den unteren Sitz wählen. Als Ergebnis erhalten wir 3 × 2 × 1 × 2 = 12 mögliche Sitzordnungen.

Schauen wir uns nun diese Möglichkeiten an, wenn die Farben rechts und links unterschiedlich sind:



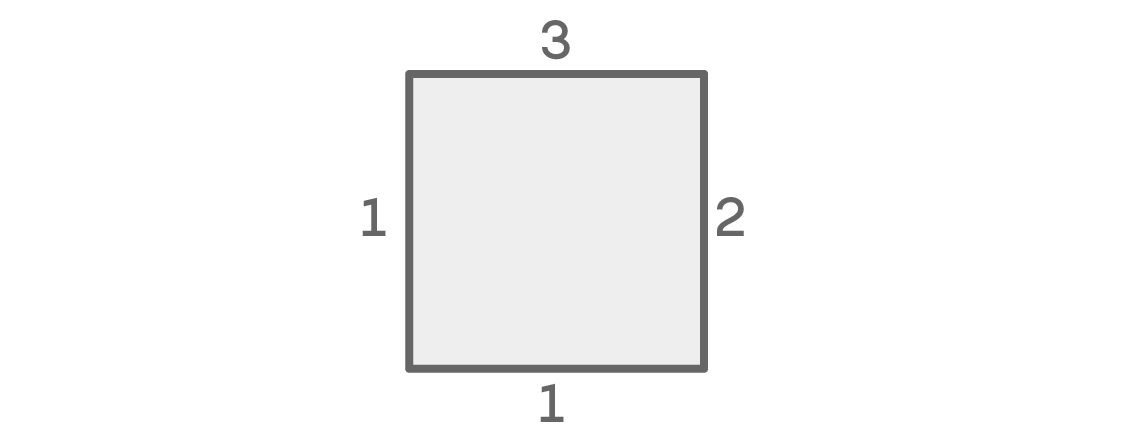
Wir haben wieder drei Optionen für die Spitze und zwei für den richtigen Ort. Der linke Ort hat wieder eine Option, aber aus einem anderen Grund: Er kann nicht derselbe sein wie der obere, benachbarte und gemäß unserem Zustand nicht der gleiche wie der rechte. Und da die Farben rechts und links unterschiedlich sind, gibt es nur noch eine Option für die untere Stelle (die gleiche wie für die obere). Dieser Fall ergibt 3 × 2 × 1 × 1 = 6 mögliche Anordnungen.

Da diese beiden Optionen alle Möglichkeiten abdecken, addieren wir sie und erhalten 12 + 6 = 18 mögliche Sitzordnungen.

Das Hinzufügen einer dritten Farbe erschwerte unsere Aufgabe, aber unsere harte Arbeit wird belohnt. Jetzt können wir diese Strategie für 4, 5 oder eine beliebige Anzahl q verschiedener Farben verwenden.

Unabhängig von der Anzahl der Farben haben wir immer zwei Fälle: links und rechts sind entweder die gleichen oder unterschiedliche Farben. Angenommen, wir haben die Wahl zwischen q Farben. Hier ist eine Tabelle, die die Anzahl der Optionen für jede Seite zeigt, falls die rechte und die linke Farbe gleich sind:



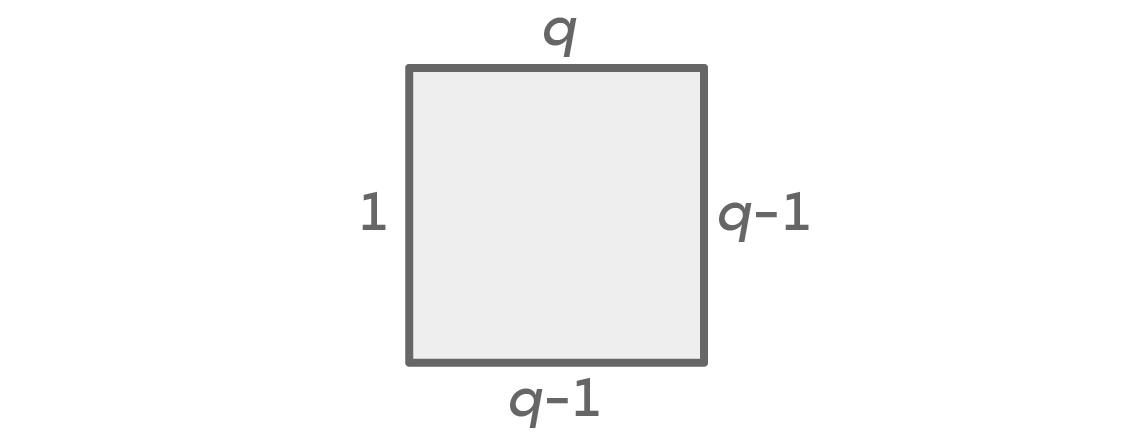
Zuerst haben wir q Farben für den oberen Sitz und q-1 für den rechten. Da wir davon ausgegangen sind, dass die Farben links und rechts gleich sind, haben wir nur eine Option für die linke Farbe. Dadurch bleiben q-1-Optionen für den unteren Punkt, da es sich um eine andere Farbe als die für den linken und rechten Punkt ausgewählte handeln kann. Das Grundprinzip der Berechnung ergibt q × (q - 1) × 1 × (q - 1) = q (q - 1) ² mögliche Layouts.

Wenn die linken und rechten Stellen unterschiedlich gefärbt sind, können wir die Möglichkeiten wie folgt berechnen:



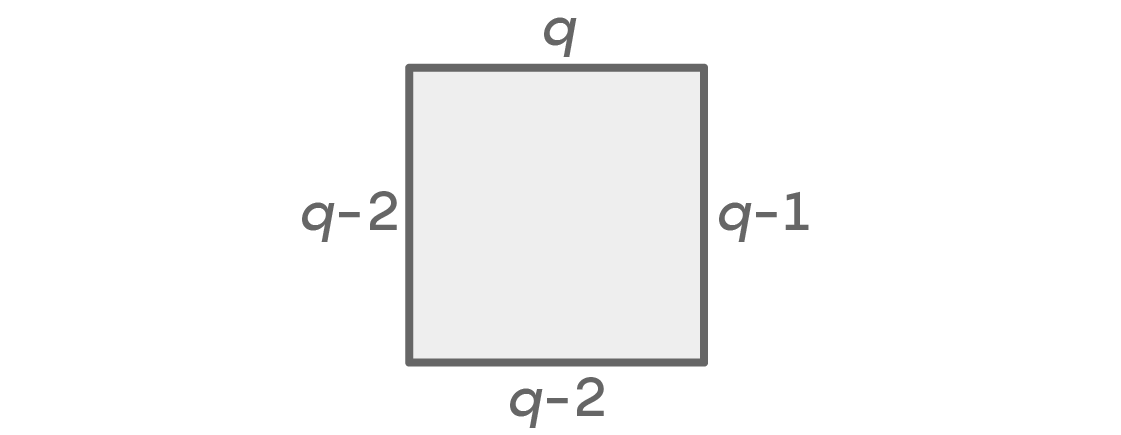
Wir haben wieder q Optionen für die Spitze und q-1 für die richtigen Stellen. Es kann nicht dieselbe Farbe auf der linken Seite geben, die für die obere und rechte Stelle ausgewählt ist, daher gibt es q-2-Optionen. Es kann eine beliebige Farbe unten geben, mit Ausnahme der beiden Farben, die wir links und rechts verwendet haben, was wiederum q-2-Optionen bietet. Wir erhalten in der Summe q × (q - 1) × (q - 2) × (q - 2) = q (q - 1) (q - 2) ² mögliche Sitzordnungen. Da diese beiden Situationen alle Optionen abdecken, addieren wir sie wie zuvor und erhalten die Gesamtzahl der möglichen Anordnungen: q (q - 1) ² + q (q - 1) (q - 2) ² .

Ein solcher Ausdruck mag wie eine seltsame Antwort auf die Frage erscheinen: "Wie viele verschiedene Sitzordnungen für verschiedene Teams am quadratischen Tisch, so dass zwei Mitglieder desselben Teams nicht nebeneinander sitzen?" Dieses Polynom enthält jedoch viele Informationen zu unserem Problem. Er gibt uns nicht nur eine quantitative Antwort, sondern zeigt auch die Struktur unserer Aufgabe auf.

Ein solches Polynom wird als „ chromatisches Polynom “ bezeichnet, weil es die Frage beantwortet: Wie viele Methoden gibt es, um die Eckpunkte eines Netzwerks (oder Graphen) so zu färben, dass ein Paar benachbarter Eckpunkte unterschiedliche Farben hat?

Ursprünglich hing unser Problem mit dem Sitzen um den Tisch herum zusammen, aber wir können es leicht in eine Frage zum Färben der Eckpunkte des Diagramms verwandeln. Anstelle von Leuten am Tisch:



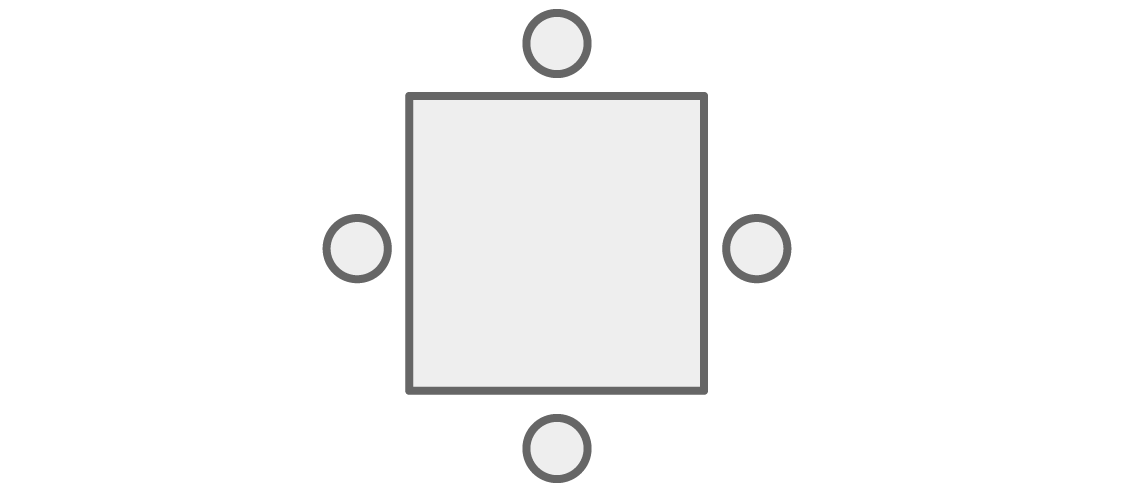
Wir werden sie uns in Form von Spitzen vorstellen, die durch Kanten verbunden sind, wenn sie neben:



Jetzt kann jede Färbung der Eckpunkte des Diagramms als Sitzplatz von Personen um das Quadrat dargestellt werden, wobei "neben" am Tisch "eine gemeinsame Kante haben" im Diagramm bedeutet.

Nachdem wir unser Problem in Form eines Graphen umformuliert haben, kehren wir zum chromatischen Polynom zurück. Wir nennen es P (q).

P (q) = q (q - 1) ² + q (q - 1) (q - 2) ²

Eine bemerkenswerte Eigenschaft dieses Polynoms ist, dass es die Farbfrage für eine beliebige Anzahl von Farben beantwortet. Um beispielsweise eine Frage mit drei Farben zu beantworten, setzen wir q = 3 und erhalten:

P (3) = 3 (3 - 1) ² + 3 (3 - 1) (3 - 2) ² = 3 × 2 ² + 3 × 2 × 1 ² = 12 + 6 = 18

Dies ist die Antwort, die wir bei drei Teams erhalten haben. Und wenn wir q = 2 setzen:

P (2) = 2 (2 - 1) ² + 2 (2 - 1) (2 - 2) ² = 2 × 1 ² + 2 × 1 × 0 ² = 2 + 0 = 2

Kommt Ihnen das bekannt vor? Dies ist die Antwort auf unser erstes Rätsel mit zwei Teams. Wir können Antworten für vier, fünf oder sogar zehn verschiedene Teams finden, indem wir einfach den gewünschten Wert für q einsetzen: P (4) = 84, P (5) = 260 und P (10) = 6 570. Das chromatische Polynom hat eine grundlegende Struktur des Problems erfasst durch Zusammenfassung unserer Zählstrategie.

Wir können weitere Details der Struktur enthüllen, indem wir algebraische Operationen an unserem Polynom P (q) = q (q - 1) ² + q (q - 1) (q - 2) ^{2 durchführen} :

= q (q - 1) (q - 1) + q (q - 1) (q - 2) ²
= q (q - 1) ((q - 1) + (q - 2) ² )
= q (q - 1) (q - 1 + q ^{2 -} 4q + 4)
= q (q - 1) (q ^{2 -} 3q + 3)

Wir haben den Faktor q (q - 1) aus jedem Teil der Summe extrahiert und ähnliche Terme kombiniert, um das Polynom auf eine faktorisierte Form zu reduzieren. Und in dieser Form kann uns das Polynom anhand seiner „Wurzeln“ etwas über die Struktur erzählen.

Die Wurzeln eines Polynoms sind Eingabewerte, bei denen es am Ausgang gleich Null wird. Es ist einfacher, die Wurzeln in der faktorisierten Form zu finden: Da das Polynom als multiplizierte Teile ausgedrückt wird, setzt jeder Wert, bei dem einer der Faktoren gleich Null ist, das gesamte Produkt zurück.

Zum Beispiel hat unser Polynom P (q) = q (q - 1) (q ² - 3q + 3) einen Faktor (q - 1). Wenn wir q = 1 nehmen, wird dieser Faktor wie das gesamte Ergebnis der Multiplikation gleich Null. Das heißt, P (1) = 1 (1 - 1) (1 ² - 3 × 1 + 3) = 1 × 0 × 1 = 0. In ähnlicher Weise ist P (0) = 0 × (–1) × 3 = 0 Daher sind q = 1 und q = 0 die Wurzeln unseres Polynoms. (Möglicherweise interessiert Sie der Faktor (q ² - 3q + 3). Da er für kein reales q gleich Null ist, gibt er unserem chromatischen Polynom keine neuen Wurzeln.)

Diese Wurzeln sind im Rahmen unseres Diagramms sinnvoll. Wenn wir dieselbe Farbe auswählen können, muss jeder Scheitelpunkt dieselbe Farbe haben. Es ist nicht möglich, das Diagramm so zu färben, dass alle benachbarten Scheitelpunkte unterschiedliche Farben haben. Genau das bedeutet, dass q = 1 die Wurzel unseres chromatischen Polynoms ist. Wenn P (1) = 0 ist, gibt es genau null Möglichkeiten, den Graphen so zu färben, dass die benachbarten Scheitelpunkte nicht die gleichen Farben haben. Gleiches gilt für die Version mit der Anzahl der Farben Null, P (0) = 0. Die Wurzeln unseres chromatischen Polynoms geben Auskunft über die Struktur unseres Graphen.

Die Fähigkeit, Struktur durch Algebra zu sehen, wird noch offensichtlicher, wenn wir andere Graphen betrachten. Schauen wir uns ein dreieckiges Diagramm an:



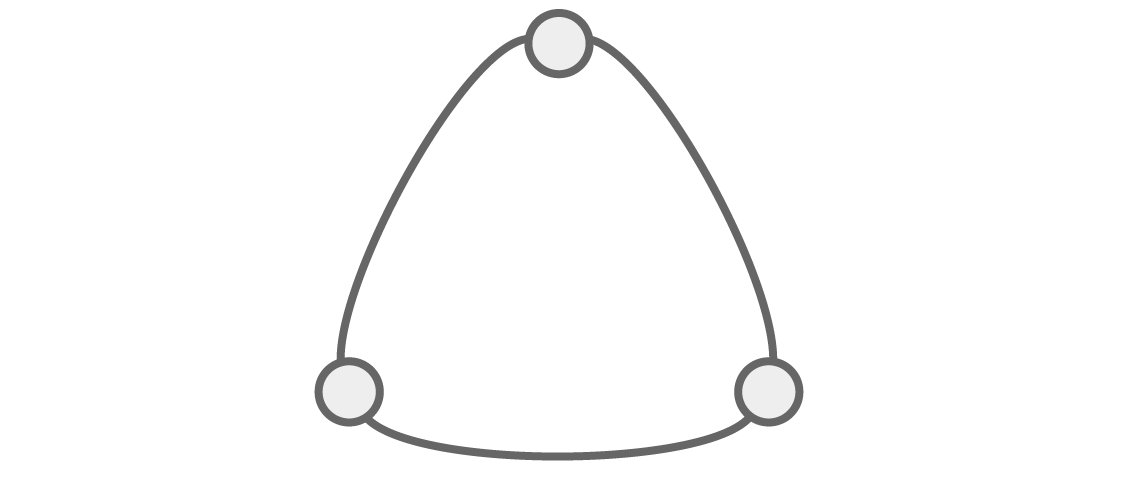
Wie viele Möglichkeiten gibt es, diesen Graphen q mit Farben zu färben, damit die benachbarten Scheitelpunkte nicht die gleichen Farben haben?

Wie üblich gibt es für die ersten beiden benachbarten Eckpunkte die Optionen q und q-1. Und da der letzte Scheitelpunkt neben den ersten beiden liegt, sollte er sich in der Farbe von beiden unterscheiden, was uns q-2-Optionen lässt. Dies gibt uns das chromatische Polynom für diesen Dreiecksgraphen: P (q) = q (q - 1) (q - 2).

In dieser Form der Faktorisierung sagt uns dieses chromatische Polynom etwas Interessantes: Es hat eine Wurzel q = 2. Und wenn P (2) = 0 ist, sollte es unmöglich sein, diesen Graphen mit zwei Farben zu färben, damit er nicht zwei benachbarte Eckpunkte derselben Farbe hat. Ist es so?

Stellen Sie sich vor, wir gehen in einem Kreis in diesem Dreieck und färben die Gipfel auf dem Weg. Wenn wir nur zwei Farben haben, müssen wir sie nach jedem Scheitelpunkt abwechseln: Wenn die erste rot ist, ist die zweite blau, was bedeutet, dass die dritte wieder rot sein sollte. Der erste und der dritte Peak sind jedoch benachbart und können nicht beide rot sein. Zwei Farben reichen nicht aus, wie das Polynom vorausgesagt hat.

Mit einem ähnlichen alternierenden Argument können wir zu einer signifikanten Verallgemeinerung kommen: Das chromatische Polynom einer geschlossenen Schleife mit einer ungeraden Anzahl von Scheitelpunkten muss eine Wurzel von 2 haben. Wenn Sie zwei Farben abwechseln und sich entlang einer Schleife ungerader Länge bewegen, haben der erste und der letzte farbige Scheitelpunkt dieselbe Farbe . Aber so wie dies eine Schleife ist, werden sie benachbart sein. Eine Färbung ist nicht möglich.

Zum Beispiel können wir verschiedene Techniken verwenden, um zu bestimmen, dass für eine Schleife mit fünf Eckpunkten das chromatische Polynom folgendermaßen aussieht: P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q. Wenn wir dies herausrechnen, erhalten wir P (q) = q (q - 1) (q - 2) (q2 - 2q + 2). Wie erwartet stellt sich heraus, dass q = 2 die Wurzel und P (2) = 0 ist. Interessanterweise beginnen Ideen in beide Richtungen zu wirken, sobald wir diese Verbindung zwischen den Graphen und ihren Polynomen finden. Polynome können uns Informationen über die Struktur von Graphen geben, und Graphen können uns Informationen über die Struktur von Polynomen geben.

Es war die Suche nach Struktur, die June Ho veranlasste, Reeds 40-Jahres-Hypothese bezüglich chromatischer Polynome zu beweisen. Die Hypothese besagt, dass, wenn wir die Koeffizienten des chromatischen Polynoms der Reihe nach auflisten und ihre Vorzeichen ignorieren, die folgende Bedingung erfüllt ist: Das Quadrat eines Koeffizienten muss mindestens das Produkt zweier benachbarter Koeffizienten sein. Zum Beispiel sehen wir im chromatischen Polynom für unsere Fünf-Scheitelpunkt-Schleife P (q) = q ⁵ - 5q ⁴ + 10q ³ - 10q ² + 4q, dass 5 ² ≥ 1 × 10, 10 ² ≥ 5 × 10 und 10 ² ≥ 10 × 4. Daraus folgt beispielsweise, dass nicht jedes Polynom chromatisch sein kann: Chromatische Polynome, die Graphen zugeordnet sind, haben eine tiefere Struktur. Darüber hinaus ermöglichte die Verbindung zwischen diesen Polynomen und anderen Bereichen Ho und seinen Co-Autoren, einige Jahre nach dem Beweis der Reed-Hypothese eine viel umfassendere Frage im Zusammenhang mit der Roth-Hypothese zu beantworten.

Vielleicht sind die Polynome am besten für ihre schlechteste Form bekannt - als abstrakte Übungen zur formalen Manipulation algebraischer Ausdrücke. Aber Polynome und ihre Eigenschaften - Wurzeln, Koeffizienten, verschiedene Formen - helfen dabei, Strukturen an unerwarteten Orten aufzudecken und Verbindungen zur Algebra in allem, was uns umgibt, herzustellen.

Übungen

1. Ein vollständiger Graph ist ein Graph, dessen Scheitelpunktpaar durch eine Kante verbunden ist. Finden Sie das chromatische Polynom eines vollständigen Graphen mit fünf Eckpunkten.


2. Suchen Sie das chromatische Polynom für das nächste Diagramm (verwenden Sie Informationen zu den chromatischen Polynomen einfacherer Diagramme).




3. Ein Graph wird zweiseitig genannt, wenn seine Scheitelpunkte in zwei Gruppen A und B unterteilt werden können, so dass Scheitelpunkte von A nur zu Scheitelpunkten B benachbart sind und Scheitelpunkte B nur zu Scheitelpunkten von A benachbart sind. Angenommen, Graph G hat ein chromatisches Polynom P. (q). Mit welcher Eigenschaft P (q) können Sie schließen, dass der Graph G zweiseitig ist?