Die Grundlagen der Blockchain verstehen: Die Herausforderung der byzantinischen Generäle. Teil 1

Die Übersetzung des Artikels wurde speziell für Studenten des Kurses „High Load Architect“ vorbereitet, der diesen Monat beginnt.

---

Blockchain ist ein dezentrales System, das aus verschiedenen Einheiten besteht, die abhängig von ihren Anreizen und den Informationen, über die sie verfügen, handeln.

Immer wenn eine neue Transaktion über das Netzwerk gesendet wird, können Knoten diese Transaktion in eine Kopie ihres Hauptbuchs aufnehmen oder ignorieren. Wenn die meisten Netzwerkteilnehmer beschließen, einen bestimmten Status zu akzeptieren, wird ein Konsens erzielt.

Ein grundlegendes Problem bei verteilten Computer- und Multiagentensystemen besteht darin, die Gesamtsystemzuverlässigkeit bei einer Reihe von nicht betriebsbereiten Prozessen zu erreichen. Dies erfordert häufig, dass die Prozesse einen Wert untereinander koordinieren, der während der Berechnung benötigt wird.

Diese Prozesse werden als Konsens bezeichnet.

• Was passiert, wenn ein Teilnehmer beschließt, die Regeln nicht zu befolgen und in den Zustand seines Hauptbuchs einzugreifen?
• Was passiert, wenn viele solcher Teilnehmer im Netzwerk sind, aber nicht die Mehrheit?

Damit ein Konsensprotokoll sicher ist, muss es fehlertolerant sein.

Zunächst werden wir kurz auf das unlösbare Problem zweier Generäle eingehen. Betrachten Sie dann das Problem der byzantinischen Generäle und diskutieren Sie die byzantinische Fehlertoleranz in verteilten und dezentralen Systemen. Lassen Sie uns ganz am Ende darüber sprechen, wie dies alles mit der Blockchain-Technologie zusammenhängt.

Die Aufgabe zweier Generäle

Diese Aufgabe, die erstmals 1975 veröffentlicht und 1978 benannt wurde, beschreibt ein Szenario, in dem zwei Generäle einen gemeinsamen Feind angreifen. Der erste General gilt als Anführer und der zweite als Anhänger. Die Armee eines jeden Generals allein reicht nicht aus, um die feindliche Armee zu besiegen, daher müssen sie gleichzeitig kooperieren und angreifen. Dieses Szenario sieht einfach aus, aber es gibt eine Einschränkung:

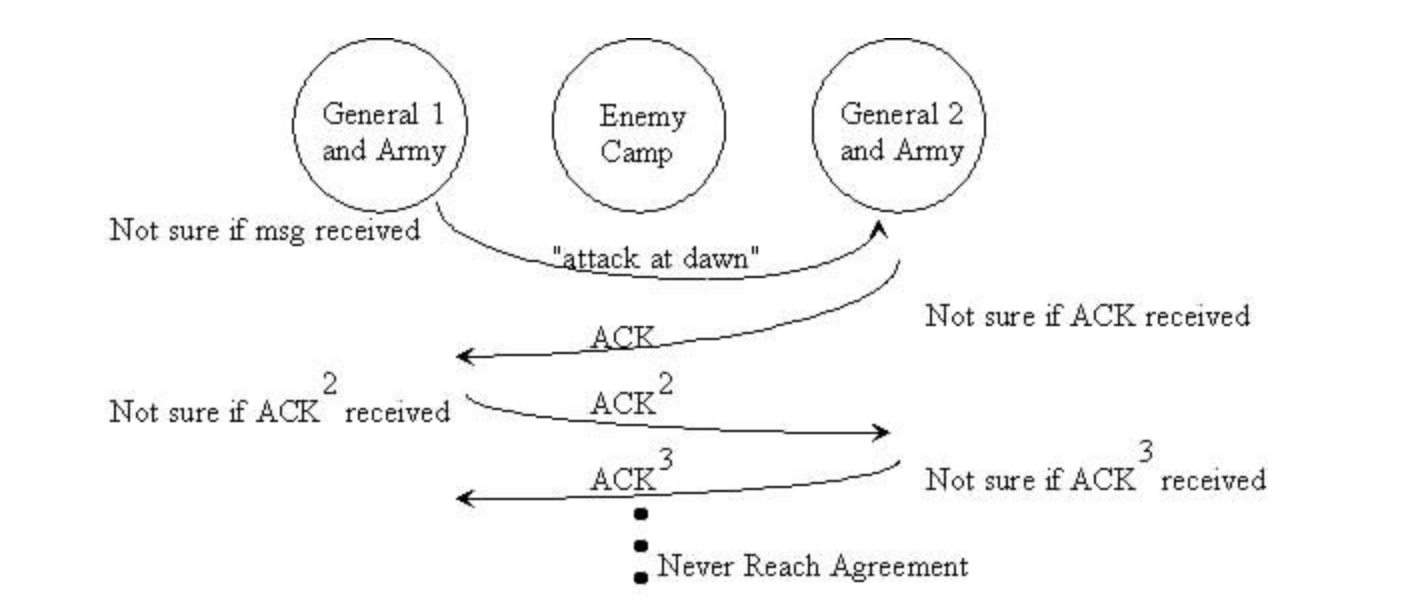
Damit sie kommunizieren und sich auf eine Zeit einigen können, muss der erste General einen Boten durch das feindliche Lager schicken und dem zweiten General eine Nachricht mit dem Zeitpunkt des Beginns des Angriffs übermitteln. Es ist jedoch wahrscheinlich, dass der Messenger von Gegnern gefangen genommen wird und die Nachricht nicht zugestellt wird. Dies wird dazu führen, dass die Armee des ersten Generals angreift und die zweite an Ort und Stelle bleibt.

Selbst wenn die erste Nachricht zugestellt wird, muss der zweite General bestätigen (ACK (Bestätigen), beachten Sie die Ähnlichkeit mit dem Drei-Wege-Handshake in TCP ), dass er die Nachricht empfangen hat, und sendet den Messenger zurück, um das vorherige Szenario zu reproduzieren, in dem der Messenger erfasst werden kann . Dies fließt in endlose ACKs, und aus diesem Grund können die Generäle keine Einigung erzielen.

Es gibt keine Möglichkeit, die zweite Bedingung zu garantieren, dh, dass jeder General völlig zuversichtlich ist, dass der andere dem Angriffsplan zustimmt. Beide Generäle werden immer nicht wissen, ob der Bote seinen Kameraden erreicht hat.



Es wurde bewiesen, dass die Aufgabe zweier Generäle unlösbar ist.

Die Aufgabe der byzantinischen Generäle

Die 1982 von Lamport, Shostak und Piz beschriebene Version dieses Problems erwies sich als Höhepunkt. Sie beschreibt dasselbe Szenario, in dem sich anstelle von zwei Generälen mehr Generäle auf den Zeitpunkt des Angriffs einigen sollten. Eine zusätzliche Komplikation besteht darin, dass ein oder mehrere Generäle Verräter sein können, dh sie können über ihre Absichten lügen (zum Beispiel sagt der General, dass er sich bereit erklärt, um 09:00 Uhr anzugreifen, dies aber nicht tut).

Das in der Aufgabe zweier Generäle beschriebene Paradigma des Leader-Followers verwandelt sich in eine untergeordnete Anordnung des Kommandanten. Um hier einen Konsens zu erzielen, müssen sich der Kommandant und jeder Untergebene auf dieselbe Lösung einigen (Angriff oder Rückzug).

Bildübersetzung:

Die Aufgabe der byzantinischen Generäle. Der Generalkommandant muss seinen n-1 Untergebenen einen Befehl senden, so dass:

• Alle loyalen untergeordneten Generäle gehorchen einem Befehl.
• Wenn der Generalkommandant loyal ist, gehorchen alle seine loyalen Untergebenen seinen Befehlen.

Neben dem zweiten Punkt muss auf eine interessante Tatsache hingewiesen werden: Wenn der Kommandant ein Verräter ist, muss noch ein Konsens erzielt werden. Infolgedessen haben alle Leutnants die Mehrheit.

Der Konsensalgorithmus basiert in diesem Fall auf der Bedeutung der meisten Entscheidungen, die Untergebene sehen.

Satz: Für jedes m erreicht der OM (m) -Algorithmus einen Konsens mit mehr als 3 Millionen Generälen und maximal m Verrätern.

Dies bedeutet, dass der Algorithmus einen Konsens erzielen kann, während 2/3 der Teilnehmer ehrlich sind. Wenn die Verräter mehr als 1/3 sind, wird kein Konsens erzielt, die Armeen können ihre Angriffe nicht koordinieren und der Feind gewinnt.

OM-Algorithmus (0)

1. Der Kommandant sendet seinen Wert an jeden der Untergebenen.
2. Jeder Untergebene verwendet den Wert, den er vom Kommandanten erhält, oder den Wert DELAY, wenn er keinen Wert erhält.

OM-Algorithmus (m), m> 0

1. Der Kommandant sendet mit seiner Wichtigkeit an jeden der Untergebenen.
2. Für jedes i sei vi der Wert, den der i-te Untergebene vom Kommandanten erhält, oder der RESET-Wert wird verwendet, wenn der Untergebene keinen Wert erhält. Der i-te Untergebene fungiert als Kommandant im OM-Algorithmus (m-1) und sendet einen Wert an jeden der n-2 verbleibenden Untergebenen.
3. Unter der Voraussetzung, dass ji ist, sei vj der Wert, den der i-te Untergebene in Schritt (2) vom j-ten Untergebenen empfangen hat (unter Verwendung des OM-Algorithmus (m-1)), oder verwendet den Wert DELAY if bekommt keine Bedeutung. Der i-te Slave verwendet den Mehrheitswert (v1, ..., vn-1).

Wenn m = 0 ist, gibt es keine Verräter, jeder Untergebene folgt der Reihenfolge. Für m> 0 geht jede endgültige Wahl eines Untergebenen vom vorherrschenden Teil der Wahl aller Untergebenen aus.
Es wird klarer, wenn Sie die Situation aus der Sicht des zweiten Untergebenen betrachten - sei C der Kommandant und L {i} der i-te Untergebene.



OM (1): Untergebener 3 ist ein Verräter. Die Situation aus Sicht des zweiten Untergebenen.

Schritte:

1. Der Kommandant sendet v an alle Untergebenen.
2. L1 sendet L2 den Wert von v oder L3 sendet L2 den Wert von x.
3. L2 ← Mehrheit (v, v, x) == v

Die endgültige Entscheidung wird mit der Mehrheit der Stimmen von L1, L2 und L3 getroffen, wodurch ein Konsens erzielt wird.

Es ist wichtig, sich daran zu erinnern, dass die meisten Untergebenen das Ziel haben, dieselbe Lösung zu wählen, anstatt eine bestimmte.

Schauen wir uns den Fall an, in dem der Kommandant ein Verräter ist.



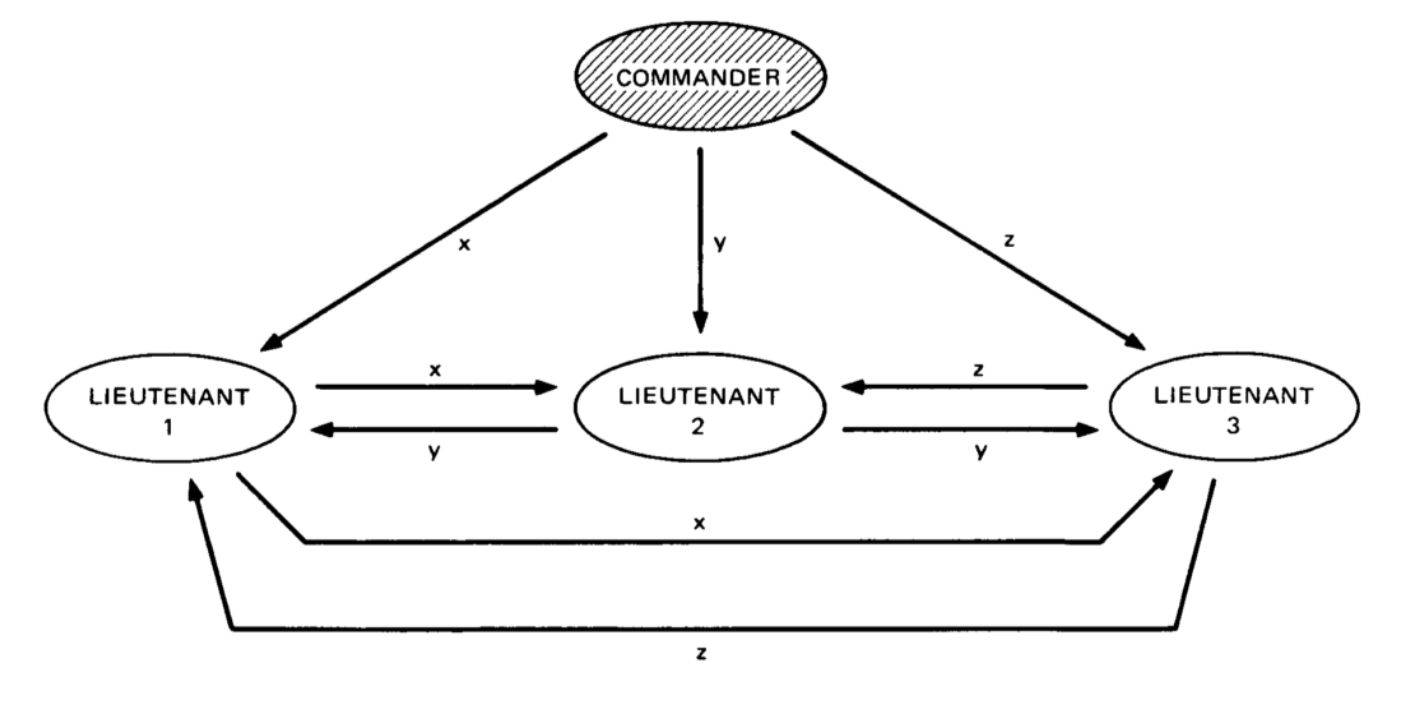OM (1): Der Kommandant ist ein Verräter.

Schritte:

1. Der Kommandant sendet L1, L2, L3 die Werte von x, y, z;
2. L1 sendet den Wert von x an die Slaves L2, L3 | L2 sendet L1, L3 den Wert von y | L3 sendet L1, L2 den Wert von z;
3. L1 ← Mehrheit (x, y, z) | L2 ← am meisten (x, y, z) | L3 ← Mehrheit (x, y, z)

Sie haben alle den gleichen Wert, so dass ein Konsens erzielt wird. Beachten Sie, dass der Mehrheitswert (x, y, z) für alle drei Untergebenen gleich ist , auch wenn die Werte von x, y, z alle unterschiedlich sind. Wenn x, y, z völlig unterschiedliche Ordnungen sind, können wir davon ausgehen, dass sie gemäß dem Standardplan - RESET - funktionieren.

Um einen praktischen Ansatz für ein komplexeres Beispiel mit 7 Generälen und 3 Verrätern zu betrachten, empfehle ich Ihnen, diesen Artikel zu lesen.

Byzantinische Fehlertoleranz

Die byzantinische Fehlertoleranz ist ein Merkmal, das ein System definiert, das eine Fehlerklasse zulässt, die zur Aufgabe "Byzantinische Generäle" gehört. Byzantinisches Versagen ist die komplexeste Klasse von Versagensarten . Es impliziert keine Einschränkungen und macht keine Annahmen darüber, welche Art von Verhalten ein Knoten haben kann (zum Beispiel kann ein Knoten beliebige Daten generieren und sich als ehrlicher Teilnehmer ausgeben).

Byzantinische Fehler sind am schwierigsten zu beheben. Byzantinische Fehlertoleranz war in Flugzeugtriebwerkssystemen, in Kernkraftwerken und in praktisch jedem System erforderlich, dessen Wirkung von den Ergebnissen einer großen Anzahl von Sensoren abhängt. Selbst SpaceX sieht darin eine potenzielle Anforderung für seine Systeme.

Der im vorherigen Abschnitt erwähnte Algorithmus entspricht der byzantinischen Fehlertoleranz, bis die Anzahl der Verräter ein Drittel aller Generäle überschreitet. Es gibt andere Möglichkeiten, um diese Aufgabe zu erleichtern, einschließlich der Verwendung digitaler Signaturen oder der Einführung von Einschränkungen für die Kommunikation zwischen Peers.

Wie hängt das alles mit der Blockchain zusammen?

Blockchain sind dezentrale Hauptbücher, die per Definition nicht von der zentralen Behörde kontrolliert werden. Aufgrund der darin gespeicherten Werte haben Angreifer einen guten wirtschaftlichen Anreiz, einen Fehler auszulösen. Trotzdem sind die byzantinische Fehlertoleranz und damit die Lösung des byzantinischen allgemeinen Problems für die Blockchain einfach notwendig.

Ohne byzantinische Fehlertoleranz kann ein Peer falsche Transaktionen übertragen und veröffentlichen, wodurch die Zuverlässigkeit der Blockchain vollständig aufgehoben wird. Erschwerend kommt hinzu, dass es keine zentrale Behörde gibt, die Verantwortung übernehmen und Schäden reparieren kann.

Als Bitcoin erfunden wurde, war ein großer Durchbruch die Verwendung von Beweisen für die probabilistische Lösung des Problems der byzantinischen Generäle. Es wurde von Satoshi Nakamoto in dieser E-Mail ausführlich beschrieben.

Fazit

In diesem Artikel haben wir einige grundlegende Konzepte des Konsenses in verteilten Systemen untersucht.