Es gibt viele Artikel im Internet mit einer Beschreibung des Gradientenabstiegsalgorithmus. Es wird noch einen geben.

Am 8. Juli 1958 schrieb die New York Times : „Ein Psychologe zeigt einen Embryo eines Computers, der darauf ausgelegt ist, zu lesen und klüger zu werden. Von der Marine entwickelt ... lernte der 704-Computer, der 2 Millionen Dollar kostete, nach fünfzig Versuchen, zwischen links und rechts zu unterscheiden ... Nach Angaben der Marine bauen sie nach diesem Prinzip die erste Denkmaschine der Perceptron-Klasse, die lesen und schreiben kann. Die Entwicklung soll in einem Jahr abgeschlossen sein, mit Gesamtkosten von 100.000 US-Dollar ... Wissenschaftler sagen voraus, dass Perceptrons später Menschen erkennen und beim Namen nennen und mündliche und schriftliche Reden sofort von einer Sprache in eine andere übersetzen können. Herr Rosenblatt sagte, dass es im Prinzip möglich ist, „Gehirne“ zu bauen, die sich am Fließband reproduzieren können und sich ihrer eigenen Existenz bewusst sind “(zitiert und übersetzt aus dem Buch von S. Nikolenko,„ Tiefes Lernen, Eintauchen in die Welt der neuronalen Netze “).

Ah, diese Journalisten wissen, wie man fasziniert. Es ist sehr interessant herauszufinden, was eine Denkmaschine der Perceptron-Klasse wirklich ist.

Binäre (binäre) Klassifikation von Objekten, künstliches Neuron der Perceptron-Klasse

Hier ist unser künstliches Neuron, das Objekte in zwei Klassen unterteilt (führt eine binäre Klassifizierung von Objekten durch):

Also haben wir:

• Eingabe: Abtastobjekt - m-dimensionaler Raumvektor $$$x = (x_1, ..., x_m)$
• Gewichte $$$w = (w_1, ..., w_m)$ eine für jedes Merkmal des Probenobjekts (auch ein m-dimensionaler Vektor)
• Innen: Addierer $$$SUM = w_1x_1 + ... + w_mx_m = \ sum _ {j = 1} ^ {m} w_ {j} x_ {j}$ - gewichtete Summe der Neuroneneingaben
• Weiter: Aktivierung $$$Φ (x, w) = Φ (SUMME)$
• Noch weiter: Quantisierer (Schwelle) - θ [Theta]
• Aktivierung + Schwelle - Vorhersage der Klassenbezeichnung eines Objekts basierend auf der gewichteten Summe der Neuroneneingaben (Objektattribute). Dieser Teil definiert die spezifische Architektur des Neurons.
• Ausgabe: Objektklassenbezeichnung (eine von zwei) $$$\ hat {y} = \ {1, -1 \}$

Klassifizierung - weil ein Neuron einem Objekt eine Klasse zuweist, binär ( binär ) - weil es nur zwei mögliche Klassen gibt.

$$$\ hat {y}$ [Spiel mit Deckel] - Wir bezeichnen den vorhergesagten (berechneten) Klassenwert für das Objekt $$$x$
$$$y$ [reguläres Spiel ohne Deckel] - wahre (bekannte) Klassenwerte für ein Objekt $$$x$ aus dem Trainingsset.

Werte $$$x$ (im Folgenden $$$x$ und $$$w$ - Dies sind keine Einheitswerte, sondern Vektoren.) variieren von Objekt zu Objekt, Gewichtskoeffizienten $$$w$ (einmal ausgewählt) bleiben unverändert. Für das Trainingsset für jedes Objekt $$$x$ Klassenlabel bekannt $$$y$ . In der Trainingsphase müssen Sie Gewichte auswählen $$$w$ damit das Modell den richtigen Wert erzeugt $$$\ hat {y}$ (fällt mit zusammen $$$y$ ) für die maximale Anzahl von Objekten im Trainingssatz. Die Annahme der Nützlichkeit eines auf diese Weise trainierten Neurons basiert auf der Hoffnung, dass es mit den ausgewählten Koeffizienten den richtigen Wert erzeugt $$$\ hat {y}$ für neue Objekte $$$x$ wahrer Klassenwert $$$y$ für die es nicht im Voraus bekannt ist.

Die intuitive Bedeutung der gewichteten Summe der Eingaben eines Neurons besteht darin, dass alle Attribute eines Objekts (jedes der Zeichen ist eine der Eingaben eines Neurons) das Ergebnis der Klassifizierung des Objekts beeinflussen, jedoch nicht alle Zeichen gleichermaßen betroffen sind. Inwieweit - bestimmen Sie das Gewicht; Das Nullstellen eines bestimmten Gewichtungskoeffizienten hebt den Beitrag des entsprechenden Attributs zum Gesamtbetrag auf, d.h. Dies ist gleichbedeutend mit dem Entfernen des Features aus dem Objekt.

Adaptives lineares Neuron ADALINE

Das ADALINE-Neuron (adaptives lineares Neuron) ist ein gewöhnliches künstliches Neuron mit dieser Aktivierungsfunktion:

$$

$$Φ (x, w) = Φ (SUM) = SUM$$

$$

$$\ Phi (x ^ {(i)}, w) = \ Phi (\ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)}) = \ sum _ { j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)}$$

Im Folgenden hochgestellt $$$i$ in Klammern wird angegeben $$$i$ Element des Trainingssatzes $$$x ^ {(i)}$ oder wahrer Klassenwert $$$y ^ {(i)}$ oder vorhergesagter Klassenwert $$$\ hat {y} ^ {(i)}$ für ihn.

Wir können sagen, dass ein solches Neuron einfach keine Aktivierungsfunktion hat und der Wert der gewichteten Summe der Eingaben dem Eingang des Quantisierers (Schwelle) zugeführt wird. Aus Gründen der Konsistenz ist es jedoch bequemer anzunehmen, dass der Wert der gewichteten Summe als Aktivierung verwendet wird.

Schwellenwert (Quantisierer) - sagt eine Klassenbezeichnung voraus:

$$

$$\ hat {y} ^ {(i)} = \ left \ {\ begin {matrix} 1, \ Phi (x ^ {(i)}, w) \ ge \ theta \\ - 1, \ Phi (x ^ {(i)}, w) <\ theta \ end {matrix} \ right.$$

Wenn der Aktivierungswert größer als ein Schwellenwert & thgr; [Theta] ist, weist der Quantisierer dem Objekt die Bezeichnung "1" zu, wenn der Aktivierungswert kleiner als der Schwellenwert & thgr; ist, erhält das Objekt die Bezeichnung "-1".

Hier können wir das Problem in erster Näherung formulieren : Wir müssen die Parameter des Neurons auswählen

• Gewichtungsfaktoren $$$w_j, j = 1, .., m$
• und Schwelle θ [Theta]

so dass Klassenwerte $$$\ hat y$ , die das Neuron den Objekten der Trainingsprobe zuordnet, stimmte mit den wahren Werten der Klassen überein $$$y$ für die gleichen Elemente (oder gab zumindest die richtige Bedeutung für die Mehrheit).

Wir transformieren die Schwellenwertfunktion ein wenig, nehmen den Fall für die Klasse $$$\ hat y = 1$ und übertragen Sie die Schwelle auf die linke Seite der Ungleichung:

$$

$$\ begin {versammelte} \ Phi (x ^ {(i)}, w) \ ge \ theta \ hfill \\\ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {( i)} \ ge \ theta \ hfill \\ - \ theta + \ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0 \ hfill \\ \ end {gesammelt}$$

bezeichnen $$$w_ {0} = - \ theta$ und $$$x_ {0} = 1$

$$

$$\ begin {versammelte} w_ {0} x_ {0} ^ {(i)} + \ sum _ {j = 1} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0 , w_ {0} = - \ theta, x_ {0} = 1 \ hfill \\\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)} \ ge 0, x_ {0} = 1 \ hfill \ end {versammelte}$$

Wie wir sehen, ist es uns gelungen, einen separaten Parameter θ zu entfernen und ihn unter dem Deckmantel eines neuen Gewichtskoeffizienten einzuführen $$$w_0$ unter dem Vorzeichen der Summe, während der Beschreibung des Objekts ein neues Dummy-Einheitszeichen hinzugefügt wird $$$x_0 = 1$ .

Wir werden die Formulierung des Problems unter Berücksichtigung der neuen Notation korrigieren.

Aufgabe ' : Wählen Sie die Parameter der Neuronengewichtungsfaktoren aus $$$w_j, j = 0, .., m$ ,
$$$x_0 = 1$ (Vorzeichenkonstante) - fiktives Neuron ( Verdrängungsneuron )

Ausgehend von dieser Stelle nummerieren wir die Vorzeichen und Gewichte c 0, nicht 1. Über den Vektor $$$w$ wir werden sagen, dass es ungefähr (m + 1) -dimensional und nicht m-dimensional ist. Vektor $$$x$ Abhängig vom Kontext können wir (m + 1) -dimensional betrachten (größtenteils in Formeln), aber denken Sie daran, dass es tatsächlich m-dimensional ist.

Warum ein Neuron ( in unserem Fall ist dies jedoch kein Neuron, sondern ein Zeichen eines Objekts oder nur eine Eingabe, aber im Fall eines mehrschichtigen Netzwerks verwandelt es sich in ein Neuron und wird normalerweise so genannt ) ist fiktiv - es ist derzeit klar. Warum er auch Verschiebung hat, wird später klar.

Die Aktivierung mit der Summe sieht nun folgendermaßen aus:

$$

$$\ Phi (x ^ {(i)}, w) = \ Phi (\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)}) = \ sum _ { j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)}, x_ {0} ^ {(i)} = 1 \ forall i$$

Der Schwellenwert ist jetzt immer 0 (Null) (der reale Wert wird in den Parameter verschoben $$$w_0$ ):

$$

$$\ hat {y} ^ {(i)} = \ left \ {\ begin {matrix} 1, \ Phi (x ^ {(i)}, w) \ ge 0 \\ - 1, \ Phi (x ^ {(i)}, w) <0 \ end {matrix} \ right.$$

Noch einmal formulieren wir das Problem mit anderen Worten (die geometrische Bedeutung des Problems)

Wenn wir uns die Formel für die Aktivierungsfunktion genau ansehen, werden wir sehen, dass es sich um eine parametrische Hyperebene im (m + 1) -dimensionalen Raum handelt, während sie in den ersten m Dimensionen mit den Punkten der Beispielelemente koexistiert und (m + 1) - Die E-Dimension ist der von den Elementen getrennte Wertebereich der Funktion.

Wenn wir nun den Aktivierungswert mit Null (Schwellenwert) gleichsetzen, ist dies auch eine Hyperebene, nur bereits im m-dimensionalen Raum, d. H. vollständig im Elementwertraum $$$x$ . Diese Hyperebene trennt die Elemente. $$$x$ in zwei disjunkte Gruppen.

Normalerweise sagen sie an dieser Stelle, dass unsere Aufgabe darin besteht, die Parameterwerte auszuwählen $$$w$ d.h. Konstruieren Sie eine m-dimensionale Hyperebene im Raum der Elemente, sodass sich die Elemente des Trainingssatzes mit dem wahren Wert der Klasse "1" auf einer Seite der Ebene und Elemente mit der wahren Klasse "-1" auf der anderen Seite befinden.

Für diejenigen, die nicht ganz verstehen, was hier geschrieben steht, lesen Sie weiter - jetzt werden wir alle sehen, dies ist zuerst. Zweitens werden wir auch sehen, dass eine solche Erklärung des Problems, obwohl sie gültig ist, nicht vollständig ist.

Eindimensionaler Raum (m = 1)

Hier beginnt der Code zu erscheinen. Wir erstellen alle Diagramme mit der üblichen Matplotlib-Bibliothek, aber hier verwende ich auch die Seaborn-Bibliothek in einer Zeile, um den Bereich des Diagramms anzupassen, weil Ich mag, wie sie es macht, aber im Prinzip kann man ohne sie auskommen.

# coding=utf-8 import matplotlib.pyplot as plt import seaborn as sns #      # (    -> ) sns.set(style='whitegrid', font_scale=1.8) #sns.set(style='whitegrid') #   ,   seaborn #plt.rcParams.update({'font.size': 16}) 

Wir nehmen viele eindimensionale Punkte und beantworten sie:

 import numpy as np import math #  -  ( ) X1 = np.array([1, 2, 6, 8, 10]) #   ( ) y = np.array([-1, -1, 1, 1, 1]) 

Hier haben wir jedes i-te Element des Arrays X1 - dies ist das i-te Element (i-ter Punkt) des Trainingsmusters (genauer gesagt sein erstes und einziges Attribut): $$$x ^ {(i)} = (X1 [i])$ , $$$x ^ {(i)} _ 1 = X1 [i]$

Jedes i-te Element des Arrays y ist die richtige Antwort, eine wahre Bezeichnung, die dem i-ten Element der Trainingsprobe mit einem einzelnen Attribut X1 [i] entspricht.

Wir nehmen nur 5 Punkte, die ersten beiden sind der Klasse "-1" zugeordnet, die restlichen drei sind der Klasse "1" zugeordnet.

Zeichnen Sie diese Punkte auf die Linie:

 #  =0 plt.plot(X1, np.zeros(len(X1)), color='black', lw=2) #     =0 plt.scatter(X1[y==1], np.full(len(X1[y==1]), 0), color='blue', marker='o', s=300, label=u' x (1 ): -1 (y=1)') plt.scatter(X1[y==-1], np.full(len(X1[y==-1]), 0), color='red', marker='s', s=300, label=u' x (1 ): -2 (y=-1)') plt.xlabel(u'X1 ( )') plt.ylabel(u' ()') plt.legend(loc='upper left') plt.show() 

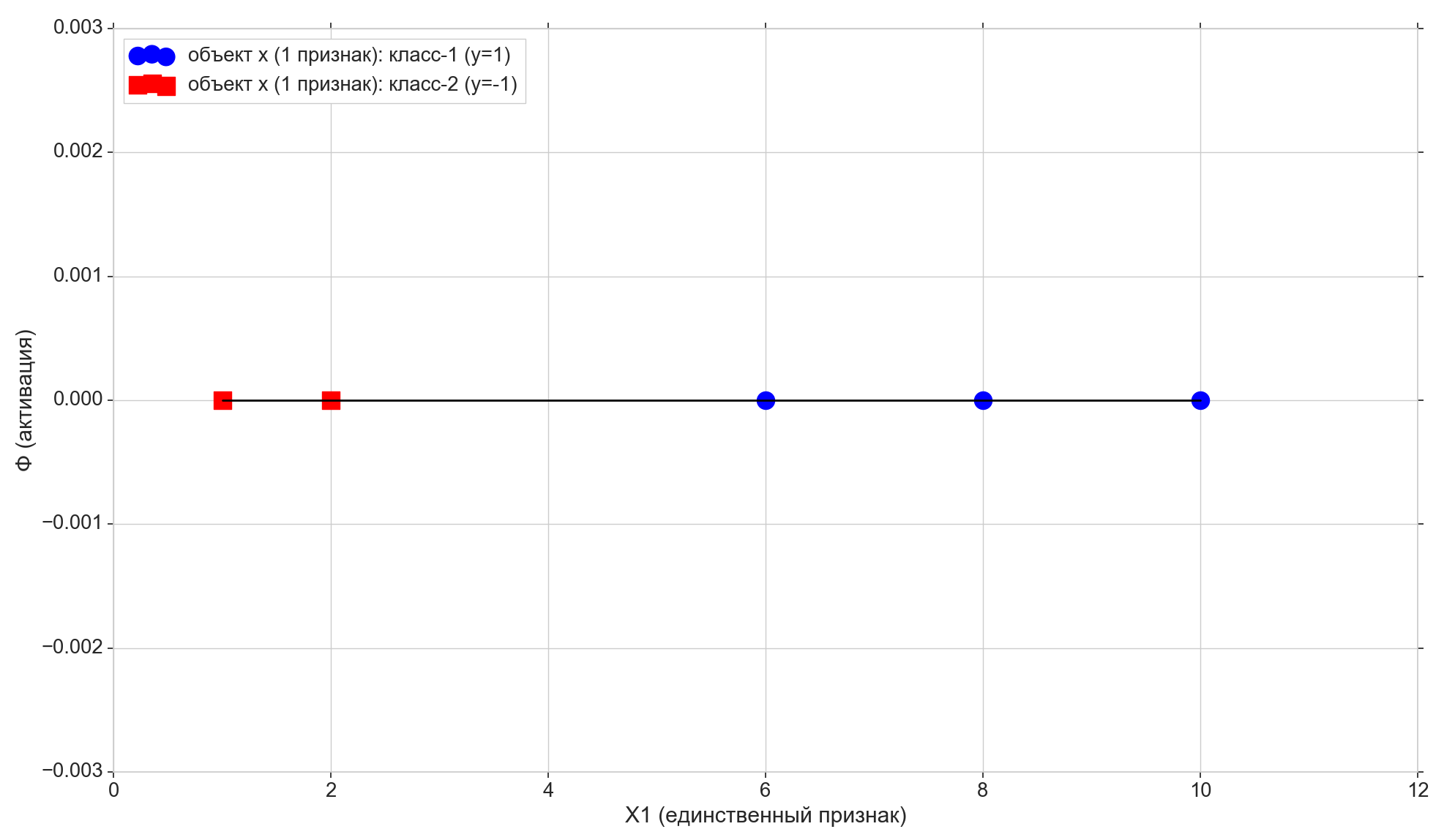
Schauen wir uns nun die Aktivierungsfunktion an:

$$

$$\ Phi = w_ {0} + w_ {1} x_ {1}$$

Wie Sie sehen können, ist dies eine gewöhnliche Parameterlinie in der Ebene (im zweidimensionalen, d. H. (M + 1) -dimensionalen Raum):

• Auf der horizontalen Achse haben wir die Punkte der Elemente (sie sind auch die Werte des Attributs X1).
• auf der Vertikalen - Aktivierungswerte für jedes Element
• Parameter $$$w_1$ - legt den Neigungswinkel fest,
• aber $$$w_0$ - Verschiebung entlang der vertikalen Achse (hier ist die Antwort auf das Scherneuron).

 w0 = -1.1 w1 = 0.4 #  y_ = w0 + w1*X1 #   (   -    ) plt.plot(X1, y_, color='violet', lw=3, label=u': w0=%0.2f, w1=%0.2f, sse/2=%0.2f'% (w0, w1, sse/2)) # :    =0 plt.scatter([-w0/w1], [0], color='violet', marker='o', s=300, label=u' ') #       plt.scatter(X1[y==1], y_[y==1], color='lightblue', marker='o', s=200, label=u': -1 (y=1)') plt.scatter(X1[y==-1], y_[y==-1], color='pink', marker='s', s=200, label=u': -2 (y=-1)') 

Denken Sie auch daran, dass unsere Aktivierungsschwelle nach einer kleinen Konvertierung auf Null gesetzt wurde. Wenn also die Projektion des i-ten Elements auf die Aktivierungslinie kleiner als Null ist, weisen wir dem Element die Klasse -1 zu ( $$$\ hat {y} = -1$ ), wenn es höher als Null ist, weisen wir die Klasse "1" zu ( $$$\ hat {y} = 1$ )

Lila Punkt - Schnittpunkt der Aktivierungslinie mit der Achse $$$\ Phi = 0$ Dies ist die sehr trennende Hyperebene (für den eindimensionalen Raum ist der Punkt die Hyperebene), die im eindimensionalen (d. h. m-dimensionalen) Merkmalsraum aufgebaut ist. Wie Sie sehen, reicht es nicht aus, die Elemente in Gruppen zu unterteilen, aber um Klassen Gruppen zuzuweisen, reicht dies nicht mehr aus. Um Elementen Klassen zuzuweisen, benötigen wir eine direkte (zweidimensionale Hyperebenen-) Aktivierung, die im 2D-Raum (dh im (m + 1) -d) -Raum „Zeichen + Aktivierung“ aufgebaut ist: die Richtung der Aktivierungsabweichung von der Vertikalen Achse bestimmt die Klasse für Gruppen von Elementen, weil Dies hängt davon ab, ob die Projektionen der Elemente bei der Aktivierung höher oder niedriger als Null sind.

Parameter ändern $$$w_0$ und $$$w_1$ Wir erhalten verschiedene Aktivierungslinien. Wir müssen eine solche Aktivierungslinie bauen, d.h. Finden Sie eine solche Kombination von Parametern $$$w$ bei dem die Projektion der ersten beiden Punkte des Trainingsmusters auf die Aktivierungslinie unter Null liegt (für sie der Wert $$$\ hat {y} = y = -1$ ), und die Projektion der verbleibenden 3 Punkte wird über Null liegen (für sie $$$\ hat {y} = y = 1$ )

Es ist ziemlich offensichtlich, dass es in unserem speziellen Fall nichts Kompliziertes gibt, eine solche Linie zu konstruieren, außerdem können solche Linien im Allgemeinen in einer unendlichen Anzahl konstruiert werden. Wir werden jedoch versuchen, es so zu erstellen, dass ein Optimalitätskriterium erfüllt ist (es kann die Qualität zukünftiger Vorhersagen beeinflussen), und es sollte die Möglichkeit bestehen, den Algorithmus auf den mehrdimensionalen Fall auszudehnen.

Hier stellen wir auch fest, dass wir speziell den anfänglichen Satz von Punkten ausgewählt haben, so dass er durch eine solche Linie geteilt werden kann (für 1-e: alle Elemente der ersten Gruppe sind kleiner, alle Elemente der zweiten Gruppe sind größer als ein fester Wert), d.h. Viele Trainingspunkte sind linear trennbar .

Fügen Sie dem Diagramm zwei weitere horizontale Linien hinzu, die den Klassen {1, -1} entsprechen, und projizieren Sie die Elemente darauf.

 #      (y=1, y=-1) plt.plot(X1, np.full(len(X1), 1), color='blue', label=u': -1 (y=1)') plt.plot(X1, np.full(len(X1), -1), color='red', label=u': -2 (y=-1)') #       (y=1, y=-1) plt.scatter(X1[y==1], np.full(len(X1[y==1]), 1), color='lightblue', marker='o', s=200, label=u' y: -1 (y=1)') plt.scatter(X1[y==-1], np.full(len(X1[y==-1]), -1), color='pink', marker='s', s=200, label=u' y: -2 (y=-1)') 

Punkte mit der Klasse "-1" projizieren in die untere Zeile $$$\ Phi = -1$ zeigt mit dem Projekt der Klasse "1" auf die oberste Zeile $$$\ Phi = 1$ .

Achten wir auf eine weitere kleine Nuance. Wir zeichnen die Aktivierungswerte entlang der vertikalen Achse auf, der Raum der Aktivierungswerte ist kontinuierlich. Das Ergebnis des Klassifikators (die Aktivierungsfunktion, die den Schwellenwert durchläuft) ist jedoch eine diskrete Menge von zwei Elementen {-1, 1} und keine kontinuierliche Skala. Hier nehmen wir eine diskrete Reihe von Klassen $$$y$ und stellen Sie es auf eine kontinuierliche Aktivierungsskala $$$\ Phi$ so dass diskrete Klassenwerte zu gewöhnlichen Punkten auf der Aktivierungsskala werden - Sonderfälle von Aktivierungswerten, die sie direkt akzeptieren oder sich ihnen annähern können. Genau genommen könnten wir zunächst nicht die numerischen Werte als Klassen verwenden, sondern die Zeichenfolgenbezeichnungen „Klasse 1“ und „Klasse 2“. In diesem Fall müssten wir die Zeichenfolgenbezeichnungen den numerischen Werten auf der Aktivierungsskala zuordnen. Daher sollten in unserem Fall die Werte der Klassen "-1" und "1" nicht als Klassenbezeichnungen verwendet werden, sondern als Zuordnung markierter Klassen zur Aktivierungsskala.

Es ist Zeit, die Fehlermetrik einzugeben

 #   -       #      plt.plot([X1, X1], [y_, y], color='orange', lw=3)#, label='err') 

Es ist natürlich zu akzeptieren, dass die Aktivierungsklasse für dieses Element umso besser vorhersagt, je näher der Aktivierungswert für das ausgewählte Element am Klassenwert für dasselbe Element liegt. Für den Fehler für das ausgewählte Element können Sie also den Abstand zwischen den Punkten nehmen - die vertikale Projektion des Elements auf die Aktivierungslinie und die Projektion des Elements auf die horizontale Linie seiner bekannten (wahren) Klasse. In der Grafik: Fehler - vertikale orange Linien.

Kosten- (Verlust-) Funktion

Wir haben eine Fehlermetrik für jeden einzelnen Artikel. Wir können daraus eine Qualitätsmetrik für die gesamte Aktivierungslinie erhalten. Es ist ganz natürlich zu akzeptieren, dass wir umso besser eine Aktivierungslinie aufgebaut haben, je kleiner die Summe der Fehler aller Elemente des Trainingsmusters ist. Für jedes einzelne Element ist der Fehler nicht minimal, aber für das gesamte Trainingsbeispiel als Ganzes können Sie Kompromisse eingehen.

Sie können jedoch nicht eine einfache Summe von Fehlern nehmen, sondern die Summe der quadratischen Fehler ( Summe der quadratischen Fehler, Summe der quadratischen Fehler, SSE ). Es ist ziemlich offensichtlich, dass, wie im Fall der Summe gewöhnlicher Fehler, je näher die Aktivierungslinie an den Punkten mit wahren Klassen von Elementen liegt, desto kleiner die Summe quadratischer Fehler ist, aber im Fall eines quadratischen Fehlers erhalten die entferntesten Elemente eine schwerere Strafe.

Was uns hier interessiert, ist nicht die Größe der Geldbuße für entfernte Elemente, sondern die Tatsache, dass die quadratische Funktion ein Minimum hat und überall differenzierbar ist (die übliche Summe hat ein Minimum, aber bei diesem Minimum ist sie nicht differenzierbar). Sehen Sie, warum dies notwendig ist. etwas später.

Also:

• Fehler - Abstand vom Klassenbeschriftungswert zur Aktivierungshyperebene
• SSE - die Summe der quadratischen Fehler aller Elemente der Trainingsstichprobe
• Kostenfunktion $$$J (w)$ - Qualitätsmetrik für die ausgewählte Aktivierungslinie. Je niedriger der Wert, desto besser die Aktivierung.

Nehmen Sie als Funktion des Wertes $$$1 \ über 2$ SSE sieht im allgemeinen Fall für ein lineares Neuron folgendermaßen aus:

$$

$$\ begin {versammelte} J (w) = {1 \ über 2} SSE = {1 \ über 2} \ sum _ {i = 1} ^ {n} (\ Phi (\ sum _ {j = 0} ^) {m} w_ {j} x_ {j} ^ {(i)}) - y ^ {(i)}) ^ {2} = {1 \ over 2} \ sum _ {i = 1} ^ {n} (\ sum _ {j = 0} ^ {m} w_ {j} x_ {j} ^ {(i)} - y ^ {(i)}) ^ {2} \ end {versammelte}$$

( $$$1 \ über 2$ Erstens stört es SSE nicht und zweitens wird es der Einfachheit halber weiter reduziert.

Hier $$$i$ - Elementnummer und $$$n$ - die Anzahl der Elemente im Trainingssatz. Ich möchte Sie daran erinnern $$$y ^ {(i)}$ - wahre Klasse $$$i$ Element der Trainingsprobe, d.h. bekannte richtige Antwort im Voraus.

Wie wir uns erinnern, wird die Position der Aktivierungslinie durch die Parameter - Gewichtungsfaktoren - bestimmt $$$w$ daher Vektor $$$w$ wirkt als Parameter der Verlustfunktion.

Für eindimensionalen Fall

$$

$$J (w) = {1 \ über 2} SSE = {1 \ über 2} \ sum_ {i = 1} ^ {n} (w_ {0} + w_ {1} x_ {1} ^ {(i) } -y ^ {(i)}) ^ {2}$$

Werte $$$x$ und $$$y$ sind im Voraus bekannt (dies ist ein Trainingssatz), daher sind sie behoben. Wir wählen die Parameter aus $$$w$ d.h. $$$w_0$ und $$$w_1$ damit der Wert $$$J (w)$ Es stellte sich als minimal heraus. Versuchen wir, das Diagramm als Wert darzustellen $$$J (w)$ hängt von den Parametern ab $$$w_0$ und $$$w_1$

 #      w0 = np.linspace(-10, 10, 200) w1 = np.linspace(-1, 1, 200) # https://docs.scipy.org/doc/numpy/reference/generated/numpy.meshgrid.html # https://stackoverflow.com/questions/36060933/matplotlib-plot-a-plane-and-points-in-3d-simultaneously ww0, ww1 = np.meshgrid(w0, w1) sse = [] for j in range(len(w1)): sse.append([]) for i in range(len(w0)): sse[j].append(((ww0[j][i]+ww1[j][i]*X1 - y)**2).sum()) sse = np.array(sse) # https://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html # https://matplotlib.org/api/toolkits/mplot3d.html from mpl_toolkits.mplot3d import axes3d fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.set_xlabel('w0') ax.set_ylabel('w1') ax.set_zlabel('J(w)') #ax.plot_surface(ww0, ww1, sse/2, color='lightblue', rstride=8, cstride=8) ax.plot_wireframe(ww0, ww1, sse/2, color='lightblue', rstride=8, cstride=8, label='SSE/2') plt.xlim(-10., 10.) plt.ylim(-1., 1.) plt.legend() plt.show() 

Im Allgemeinen ist hier bereits sichtbar, dass die Verlustfunktion ein Minimum hat und wo sie sich ungefähr befindet. Aber lassen Sie uns noch einen Trick machen und dasselbe Diagramm erstellen, nur mit einer logarithmischen vertikalen Skala .

 #ax.plot_surface(ww0, ww1, np.log(sse/2), color='lightblue', rstride=8, cstride=8) ax.plot_wireframe(ww0, ww1, np.log(sse/2), color='lightblue', rstride=8, cstride=8, label='log(SSE/2)') 

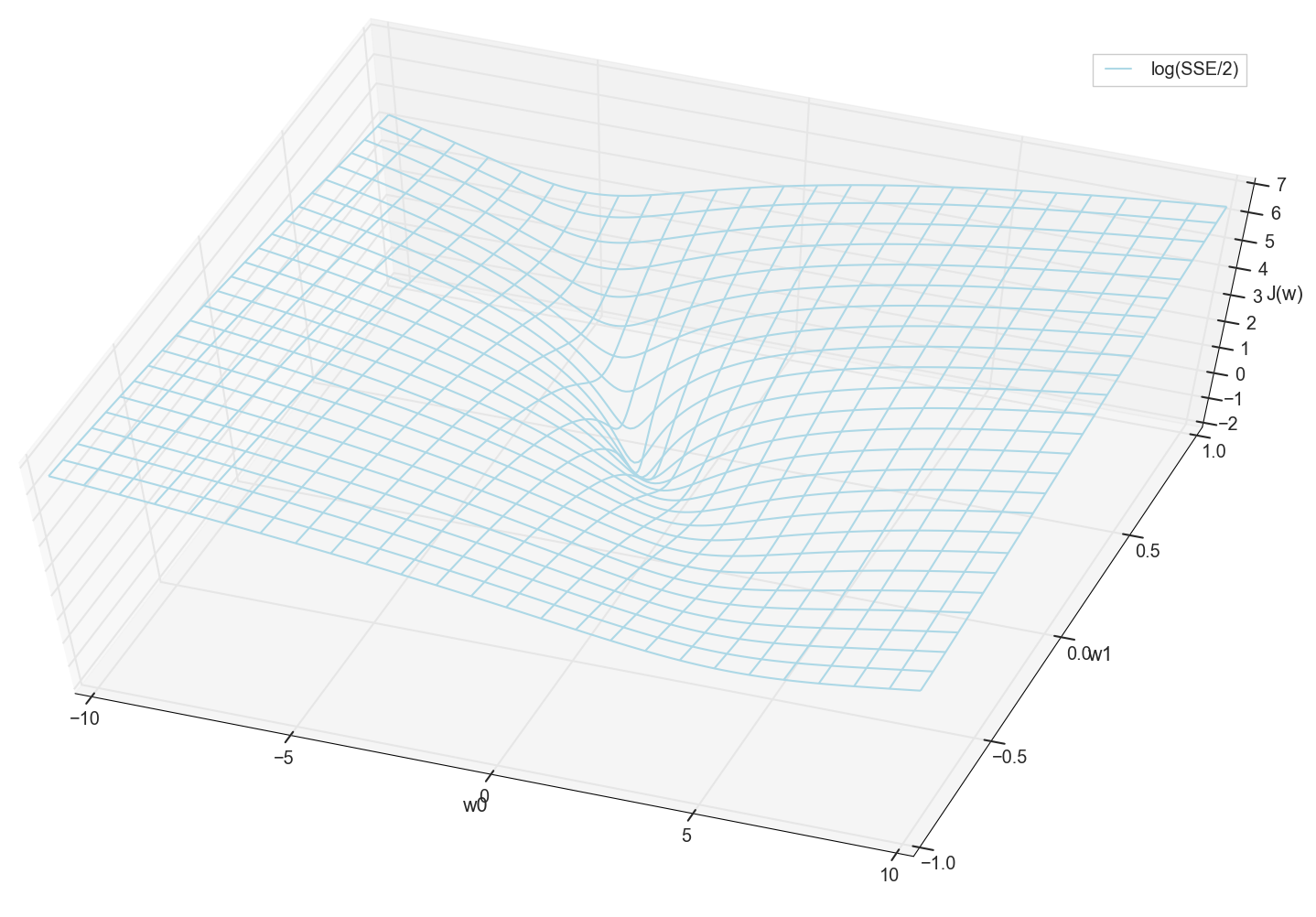
Ich weiß nichts über dich, aber als ich dieses Diagramm zum ersten Mal sah, erlebte ich Erleuchtung. Diese natürliche Höhle ist nicht nur eine figurative Visualisierung mehrdimensionaler Hügel aus einem beliebten Artikel über neuronale Netze, sondern eine echte Grafik.

Unsere Aufgabe ist es, solche Werte auszuwählen $$$w_0$ und $$$w_1$ um dieser Grube auf den Grund zu gehen. Wir bekommen die Werte von Gewichten - wir bekommen ein trainiertes Neuron.

Da wir alle gleich einen Graphen gezeichnet haben und sein Minimum persönlich beobachten, wird uns niemand verbieten, seine Koordinaten durch eine einfache Aufzählung im Raster "manuell" zu finden:

 #      # https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.min.html # https://docs.scipy.org/doc/numpy/reference/generated/numpy.amin.html#numpy.amin # https://docs.scipy.org/doc/numpy/reference/generated/numpy.argmin.html min_ind = np.unravel_index(np.argmin(sse), sse.shape) #  -  #ax.scatter(ww0[min_ind], ww1[min_ind], sse[min_ind]/2, color='red', marker='o', s=100, ax.scatter(ww0[min_ind], ww1[min_ind], math.log(sse[min_ind]/2), color='red', marker='o', s=100, label='min: w0=%0.2f, w1=%0.2f, SSE/2=%0.2f' % (ww0[min_ind], ww1[min_ind], sse[min_ind]/2)) 

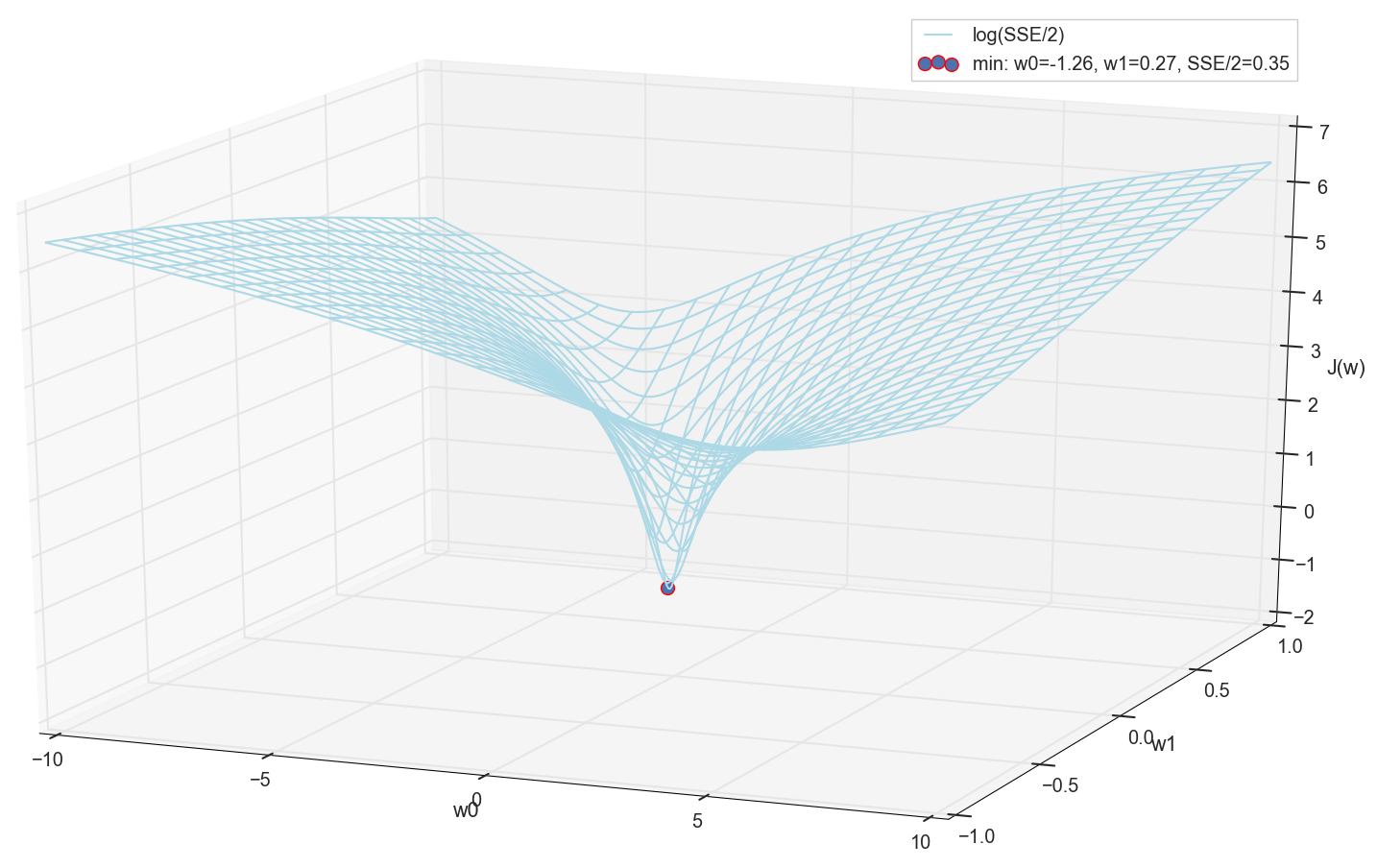
Dies sind die Werte: $$$w_0 = -1,26$ und $$$w_1 = 0,27$ beträgt die Summe der quadratischen Fehler der SSE 0,69, die Kostenfunktion $$$J (w) = SSE / 2 = 0,35$ (genauer: 0,3456478371758288).

Mal sehen, wie die Aktivierung mit diesen Parametern aussieht:

 #  ""   (SSE=0.69, sse/2=0.345) w0 = -1.26 w1 = 0.27 

Für mich ist das ganz normal. Der Schnittpunkt der Aktivierung mit einem Schwellenwert von Null trennt Elemente aus verschiedenen Klassen, und die Aktivierung selbst weist ihnen die richtigen Werte zu. Gleichzeitig scheint die Aktivierung in einer optimalen Position zu sein.

Bevor wir fortfahren, bewundern wir noch einmal die Grafik im Raster weiter:

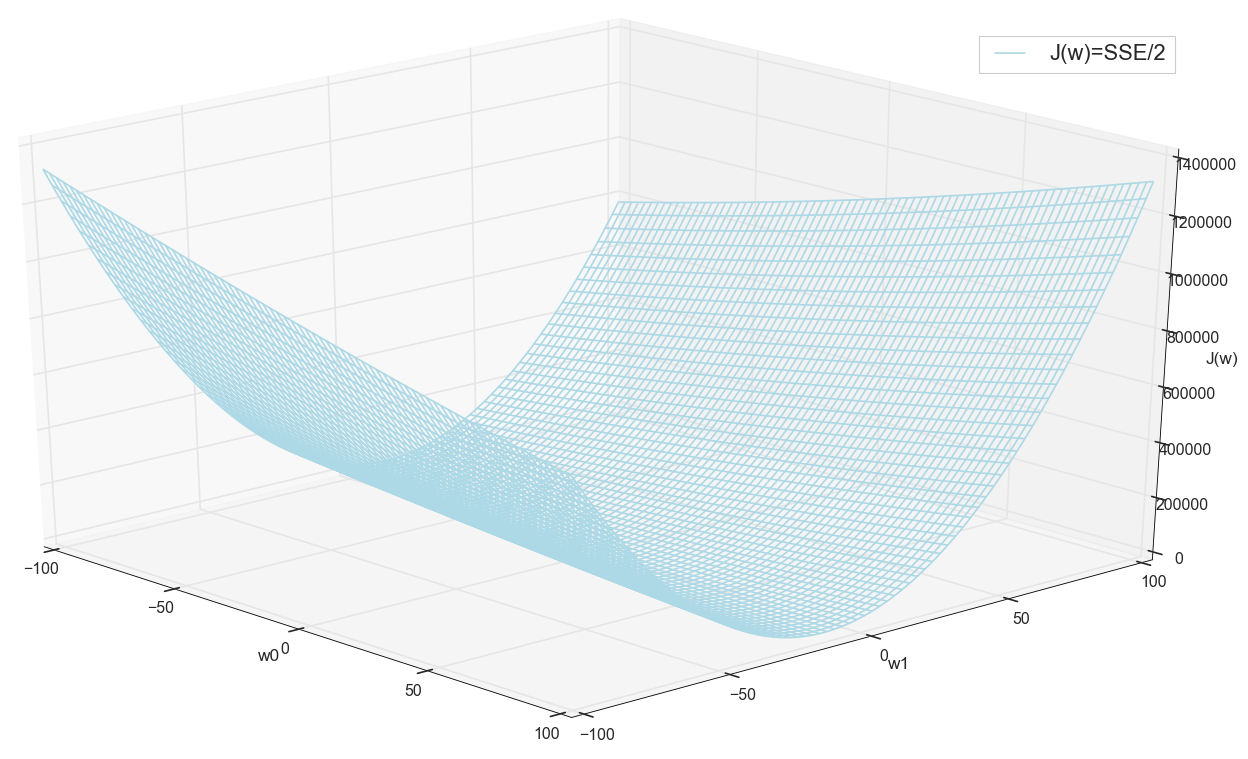
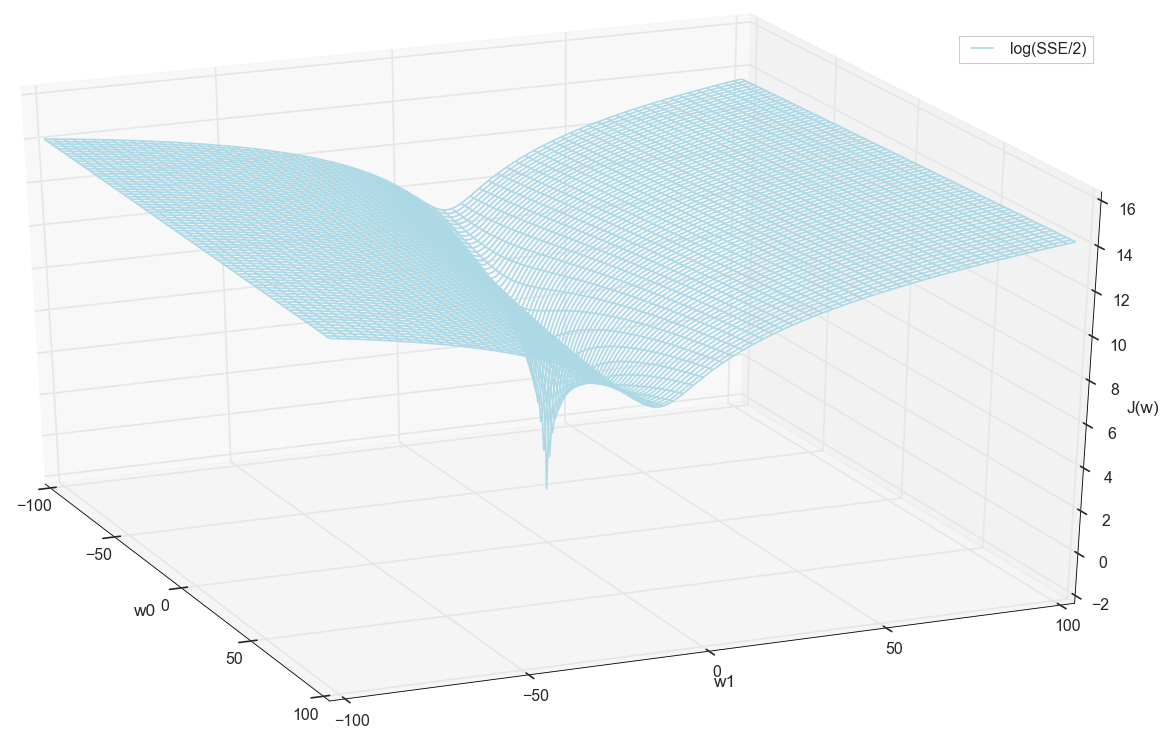
Es scheint, dass es keine anderen Tiefs in der Nähe gibt, die gedacht hätten.

Minimale Suche

Wir haben also Gewichte - die Koordinaten des minimalen Fehlerwerts. Dies ist der optimale Wert der Gewichte auf dem Trainingsmuster. Im Allgemeinen ist dies genau das, was wir brauchen. Wir können sagen, dass das Neuron trainiert ist. Vielleicht kann dies abgeschlossen werden?

Suche nach einem Minimum: Suche nach Raster

• Die Option auf den ersten Blick funktioniert ziemlich gut (wie wir sehen)
• Sie müssen im Voraus wissen, in welchem ​​Bereich Sie nach einem Minimum suchen müssen (Sie können ziemlich große Ränder nehmen und dann den Suchbereich eingrenzen - dies ist nur mit dem Auge möglich).
• Um die Genauigkeit zu erhöhen, müssen Sie den Schritt → noch mehr Punkte verringern (Lösung: Sie können den Suchbereich iterativ eingrenzen).
• Zu viele Punkte (für 2d mag es in Ordnung sein, aber für mehrdimensionale Fälle stoßen wir sehr schnell auf Ressourcen)
• Für MNIST (28 x 28 = 784 Pixel - dieselbe Anzahl von Eingaben, dieselben Gewichtungsfaktoren plus Versatz, ein Raster von 100 Schritten pro Dimension): 100 ^ 785 = 10 ^ 1570.

Wenn wir also ein einzelnes Neuron (nicht einmal ein neuronales Netzwerk) in einem Bild von 28 x 28 = 784 Pixel trainieren möchten, indem wir durch direkte Aufzählung in einem Raster von 100 Punkten für jede Messung nach einem Minimum suchen, müssen wir 10 ^ 1570 Kombinationen aussortieren. Dies ist ziemlich viel für die Speicherung und Suche (im sichtbaren Teil des Universums gibt es nur 10 ^ 80 Atome, das Universum existiert für ungefähr 4 * 10 ^ 17 Sekunden = 4 * 10 ^ 26 Nanosekunden).

Versuchen wir, schneller eine Option zu finden.

Minimale Suche: Konstanter Abstieg

Schauen wir uns das Diagramm der Verlustfunktion an $$$J (w)$ im Flugzeug: fix $$$w_0$ ändern $$$w_1$

 def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum() #  w0,   J(w1)=sse(w1)/2 w1 = np.linspace(-1, 1, 200) sse = [[], [], []] for i in range(len(w1)): sse[0].append(sse_(X1, y, -1, w1[i])) sse[1].append(sse_(X1, y, 0, w1[i])) sse[2].append(sse_(X1, y, 1, w1[i])) sse = np.array(sse) plt.plot(w1, sse[0]/2, color='orange', label='w0=-1') plt.plot(w1, sse[1]/2, color='blue', label='w0=0') plt.plot(w1, sse[2]/2, color='red', label='w0=1') plt.xlabel('w1') plt.ylabel('J(w)') plt.legend() plt.show() 

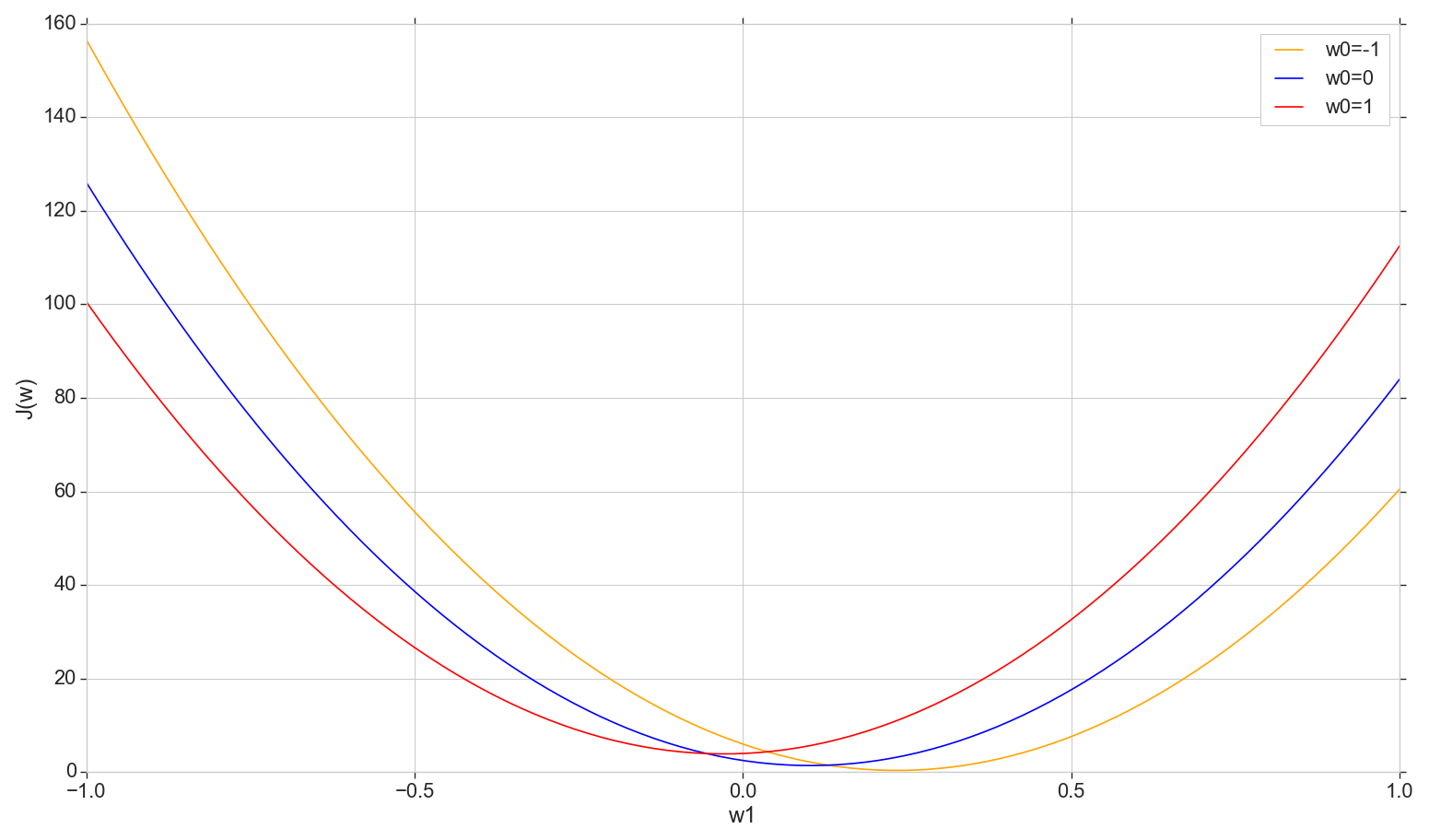
Dies ist eine gewöhnliche Parabel (genauer gesagt eine Familie von Parabeln - sie unterscheiden sich geringfügig, je nachdem, auf welchen Wert sie festgelegt ist $$$w_0$ ) Um die minimale Parabel zu finden, müssen nicht alle Punkte sortiert werden. Wir können einen beliebigen Punkt auf der horizontalen Achse wählen und uns mit einem Schritt zum Minimum bewegen.

Betrachten Sie eine Option mit konstanter Tonhöhe

• Wenn der Schritt zu groß ist, können Sie ihn verfehlen und das Minimum nicht erreichen (der Schritt kann reduziert werden).
• Wenn es zu klein ist, gibt es zu viele Schritte (mehr als es sein könnte)
• In jedem Fall werden wir nicht das genaue Minimum erreichen, aber wir können es mit willkürlicher Genauigkeit erreichen, indem wir den Schritt in der Nähe des gefundenen ungenauen Minimums ändern (der Schritt hört auf, konstant zu sein).
• Wir kennen die Abstiegsrichtung nicht (es ist möglich, algorithmisch zu lösen: Gehen Sie nicht in Richtung zunehmender Fehler).
• Das Problem beim Auffinden der Reichweite wurde behoben (Sie können von überall aus nach unten gehen - früher oder später werden wir sowieso nach unten gehen).
• Im Prinzip funktioniert die Option, aber vielleicht gibt es eine bessere Option?

Hinweis: Als ich über eine solche Möglichkeit des Abstiegs zu einer Vorlesung sprach, fragte ein Student, warum Sie schrittweise vorgehen müssen, wenn Sie anhand der Formel sofort eine Mindestparabel finden können. Zuerst habe ich etwas in dem Sinne beantwortet, dass wir jetzt daran interessiert sind, die Iterationsoption in Betracht zu ziehen, damit wir sie später nicht nur mit einer Parabel, sondern auch in anderen Situationen verwenden können. Außerdem benötigen wir in diesem Abschnitt nicht mindestens eine Parabel - wir werden uns nicht in einer Dimension, sondern in allen Dimensionen auf ein Minimum bewegen, sodass bei jeder neuen Iteration ein neuer Schritt nicht entlang dieser Parabel, sondern weiter stattfindet Parabel mit einer neuen Scheibe mit einem verschobenen Wert $$$w_0$ . Aber später dachte ich, dass im Prinzip nichts falsch ist, wenn wir uns bei jedem Slice bewegen, nicht in Schritten, sondern sofort auf das Minimum des aktuellen Slice herunterrollen. Also müssen wir immer wieder, Messung für Messung, immer noch auf ein globales Minimum rutschen, und es scheint schneller als die Schritte zu sein. Für ein einzelnes Neuron sollte es funktionieren und nicht nur mit einer Parabel. Aber ich habe noch nicht angefangen, Zeit damit zu verschwenden, diese Theorie zu testen, also gehen wir hier einfach weiter - ich habe versprochen, über Gradientenabstieg zu sprechen.

Suche nach einem Minimum: Gefälle

Im Allgemeinen gehen wir die Stufen hinunter, aber wir machen es klüger. Wir verwenden die Ableitung der Kostenkurve, um den Schritt auszuwählen (hier nicht die Kostenkurve , sondern die Kostenkurve ).

• Wir haben mehrere Dimensionen und jede hat ihre eigene Kurve: Wir reparieren alles $$$w_j$ außer $$$w_k$ ,
• $$$J (w_k)$ es wird eine Fehlerkurve in geben $$$k$ th Dimension
• Alle von ihnen sind (in unserem Fall) Parabeln, aber im Allgemeinen ist es nur wichtig, dass sie überall differenzierbar sind und ein Minimum haben
• Um den Schritt in jeder Messung anzupassen, verwenden wir die partielle Ableitung der Fehlerfunktion in Bezug auf diese Messung (einen variierenden Koeffizienten) $$$w_k$ )
• Ein Vektor solcher partiellen Ableitungen wird als Gradient bezeichnet.

Das ist alles gut, aber woher kommt die Ableitung? Jetzt lass es uns herausfinden.

Die geometrische Bedeutung der Ableitung

Für mich blieb das Derivat lange Zeit eine Reihe spezieller Formeln und Regeln für seine Berechnung sowie etwas über die Zunahme, Abnahme und Extreme. Es ist hier angebracht, sich daran zu erinnern oder herauszufinden, was das Derivat tatsächlich ist.

Ableitungsfunktion $$$y (x)$ an diesem Punkt $$$x_0$ Ist die Grenze des Verhältnisses des Inkrements der Funktion $$$\ Delta y$ zum Argumentinkrement $$$\ Delta x$ beim Inkrementieren eines Arguments $$$\ Delta x$ gegen Null tendieren:

$$

$$y '(x_0) = \ lim _ {\ Delta x \ bis 0} {\ Delta y \ über \ Delta x}, \ Delta y = y (x_0 + \ Delta x) - y (x_0)$$

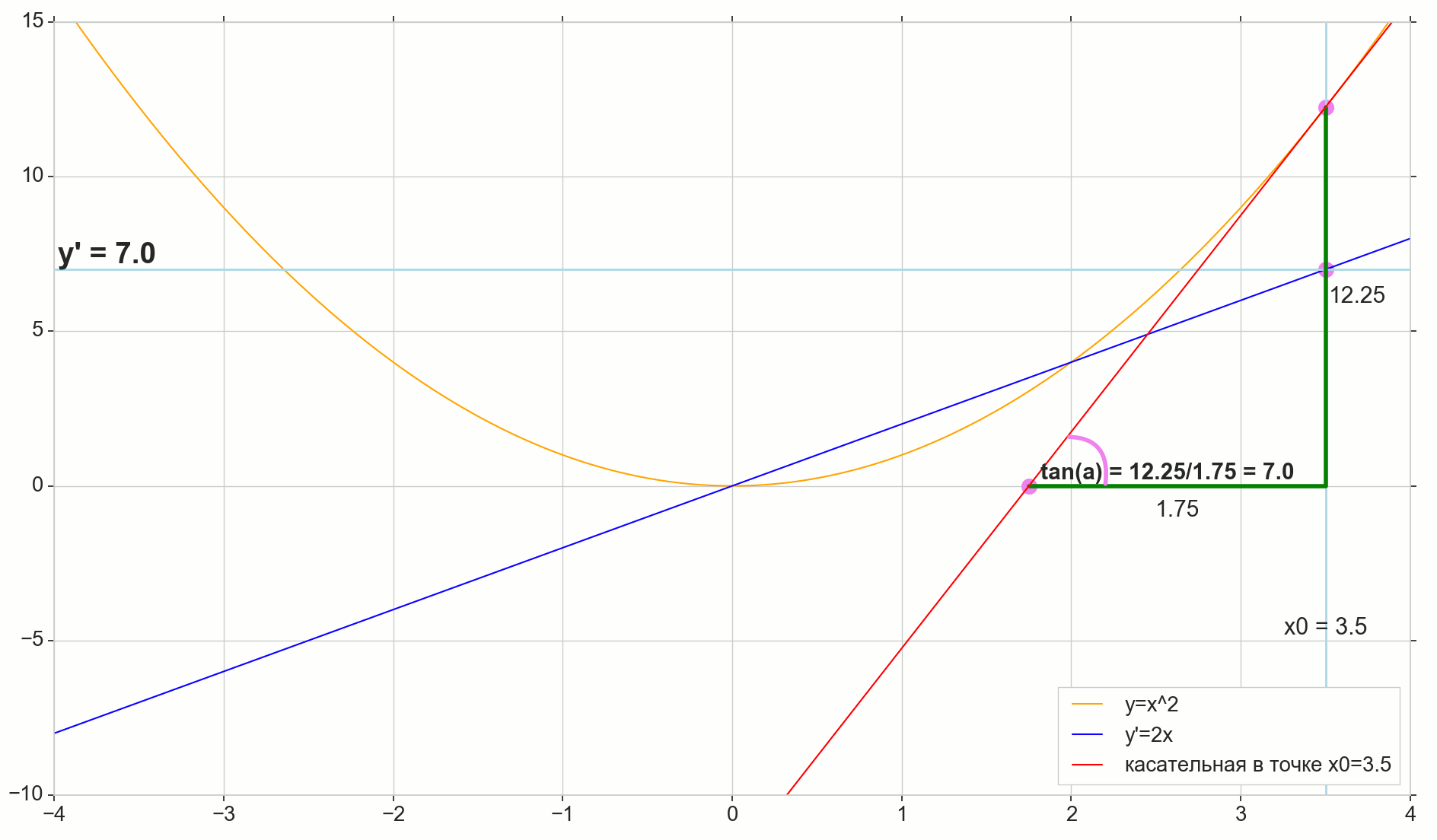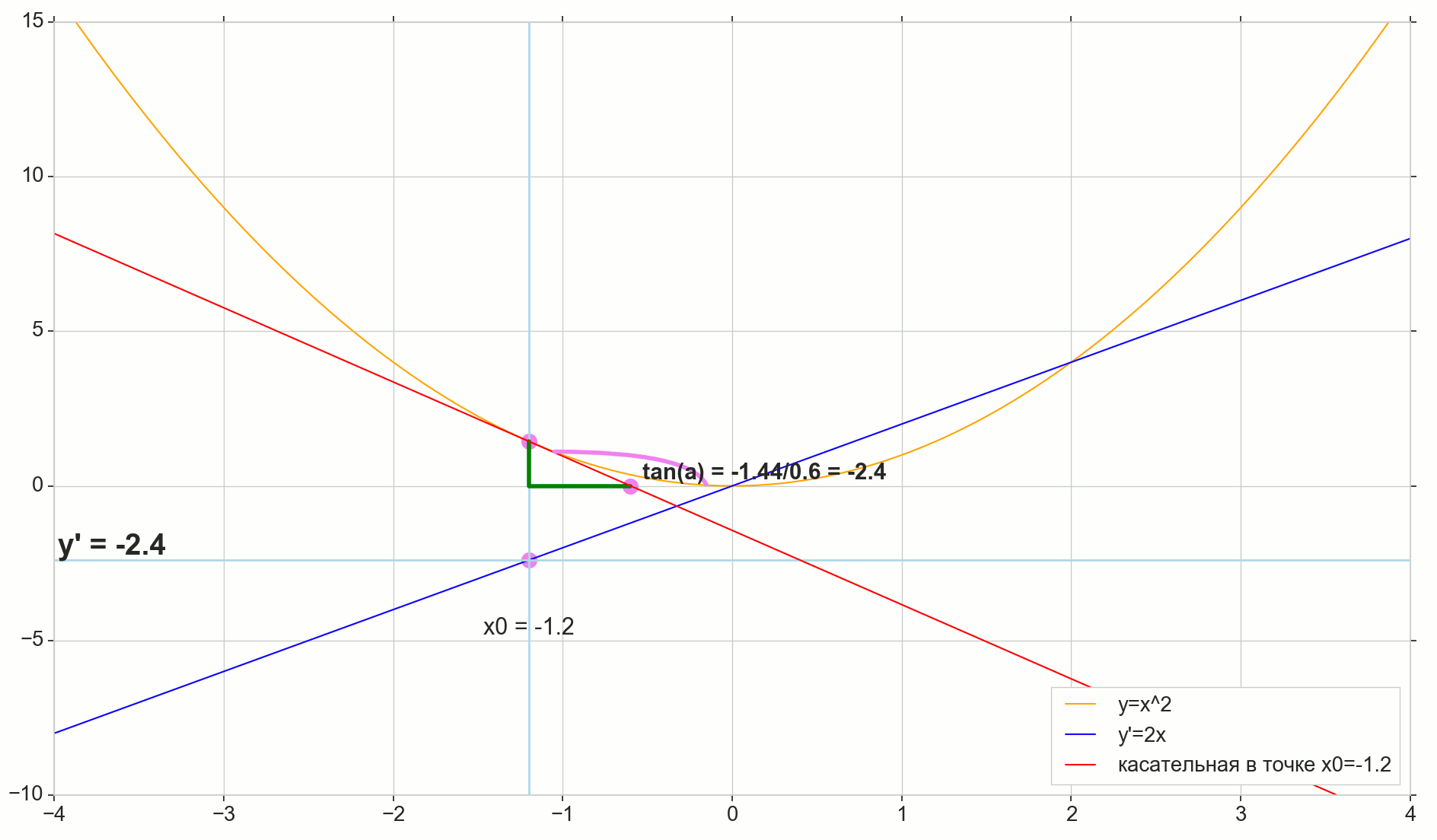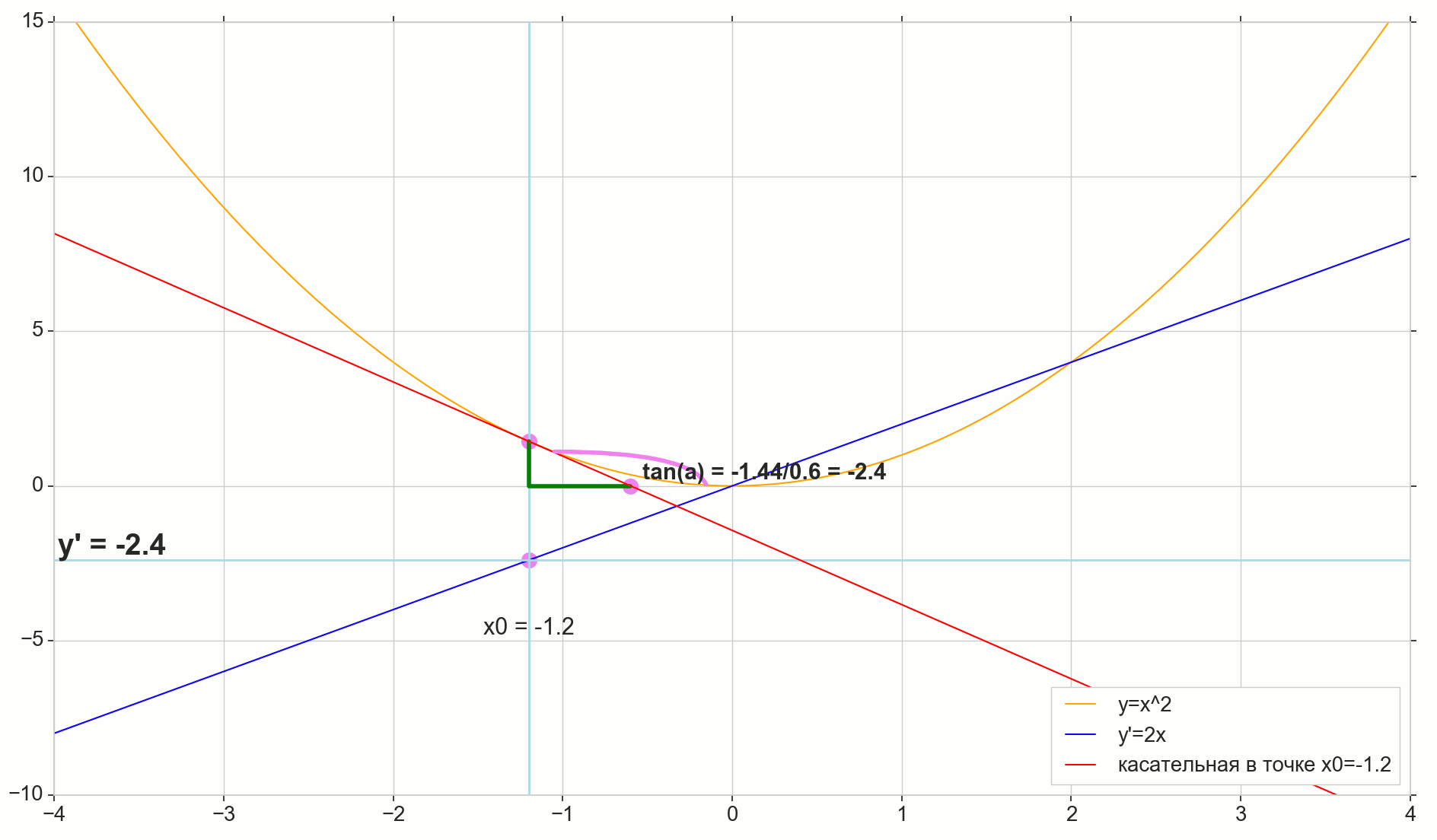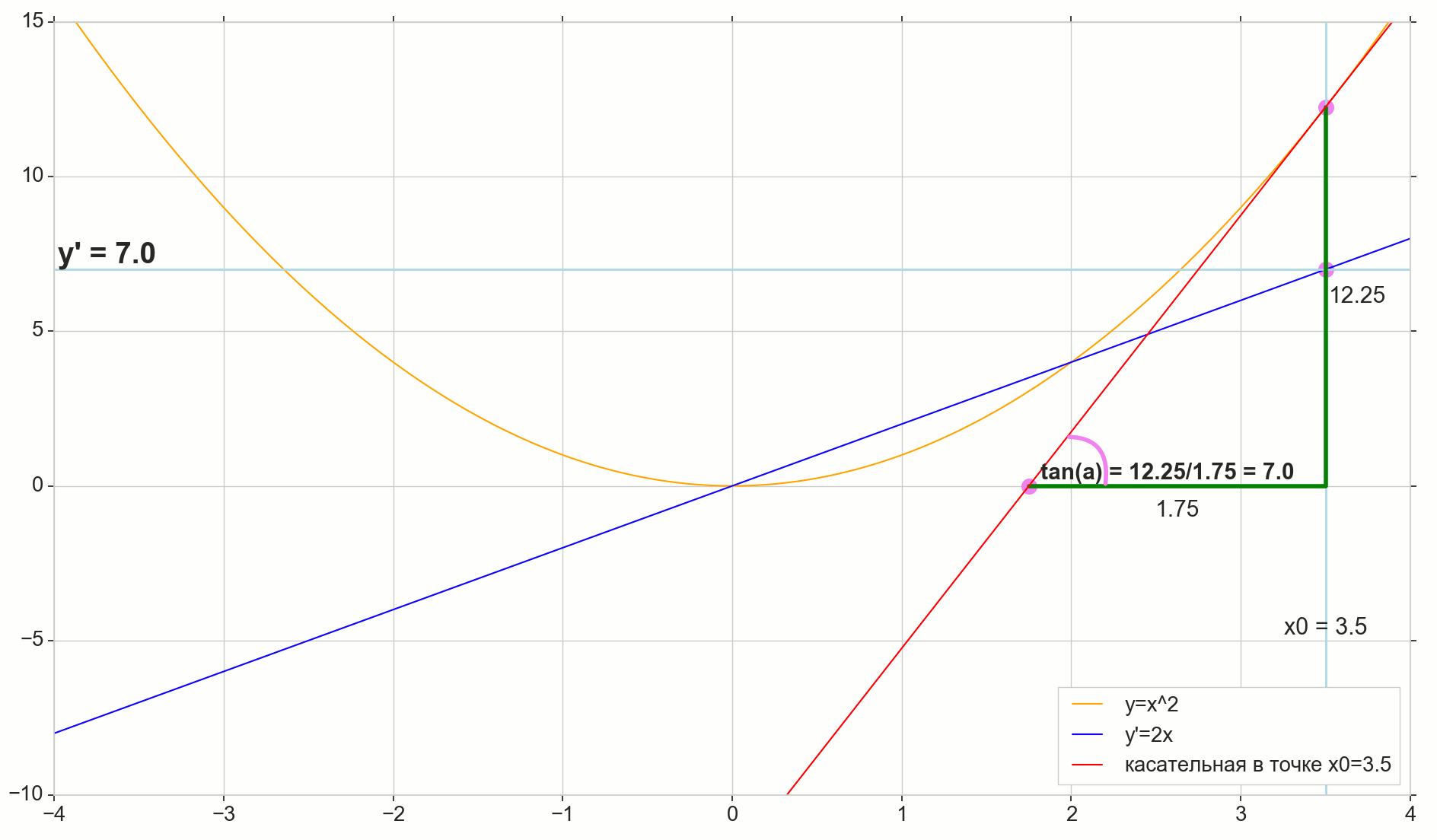
Der Punkt im Bild $$$M (x_0, y (x_0)) = (x_0, y_0)$ Ist der Punkt, an dem wir die Ableitung bestimmen wollen. Punkt $$$N (x_0 + \ Delta x, y (x_0 + \ Delta x)) = (x_0 + \ Delta x, y_0 + \ Delta y)$ - Punkt, der durch Inkrementieren des Arguments erhalten wird $$$\ Delta x$ . Direkt $$$Mn$ - Sekante durch diese beiden Punkte.

Punkt $$$A$ - Schnittpunkt der Sekante $$$Mn$ mit horizontaler Achse $$$y = 0$ .

Betrachten Sie zwei rechtwinklige Dreiecke: ein Dreieck $$$\ Dreieck NPM$ mit Abschnitt Sekante $$$Mn$ als Hypotenuse und Dreieck $$$\ triangle MBA$ mit der Fortsetzung der Sekante zur Achse $$$y = 0$ - Segment $$$AM$ als Hypotenuse. Aus dem Grafik- und Schulgeometriekurs geht hervor, dass die Winkel $$$\ angle NMP$ und $$$\ angle MAB$ sind gleich, und deshalb sind ihre Tangenten gleich:

$$

$$\ tan \ angle MAB = \ tan \ angle NMP = {MB \ über AB} = {NP \ über MP} = {\ Delta y \ über \ Delta x}$$

Zum Bild hinzufügen: $$$MD$ - Tangente an die Anfangskurve am Punkt $$$M$ kreuzt eine Achse $$$y = 0$ an der Stelle $$$D$ . Dreieck $$$\ triangle MBD$ - ein rechtwinkliges Dreieck mit Hypotenuse - Kassettenabschnitt, Segment $$$MD$ .

Wir zielen auf das Inkrement $$$\ Delta x$ auf Null:

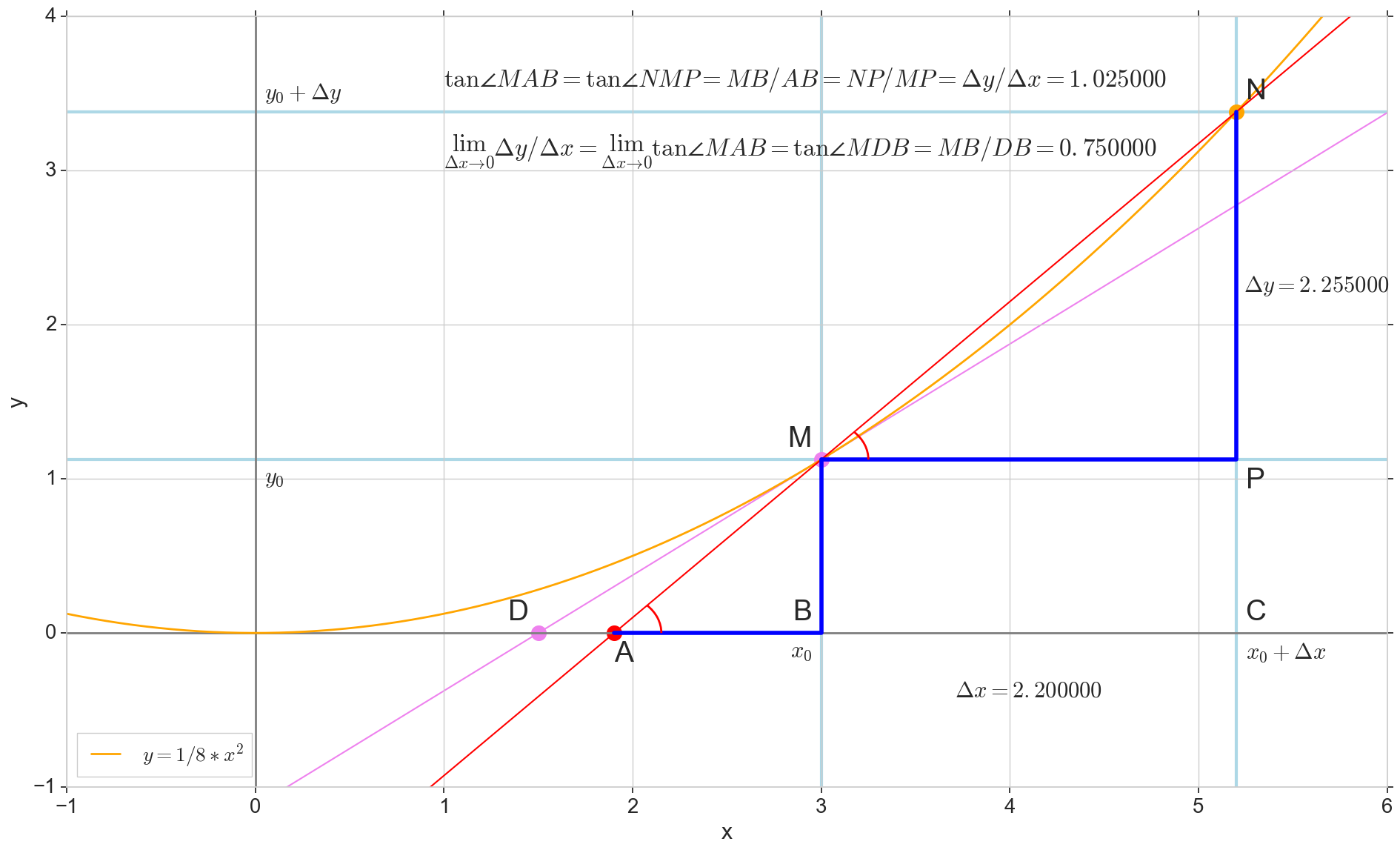
Punkt $$$N$ auf den Punkt bewegen $$$M$ nach Funktion Punkt $$$A$ schleicht sich zu einem Punkt $$$D$ entlang der Achse $$$y$ Sekante $$$Mn$ verwandelt sich in eine Tangente $$$MD$ mit Berührungspunkt $$$M$ . Quellendreieck $$$\ Dreieck NPM$ mit Beinen $$$\ Delta x$ und $$$\ Delta y$ schrumpft auf einen Punkt, aber ein Dreieck wie es $$$\ triangle MBA$ verwandelt sich in ein Dreieck $$$\ triangle MBD$ Erhalt nicht nur makroskopischer Dimensionen, sondern auch Winkelgleichheit $$$\ angle MAB$ und $$$\ angle NMP$ .

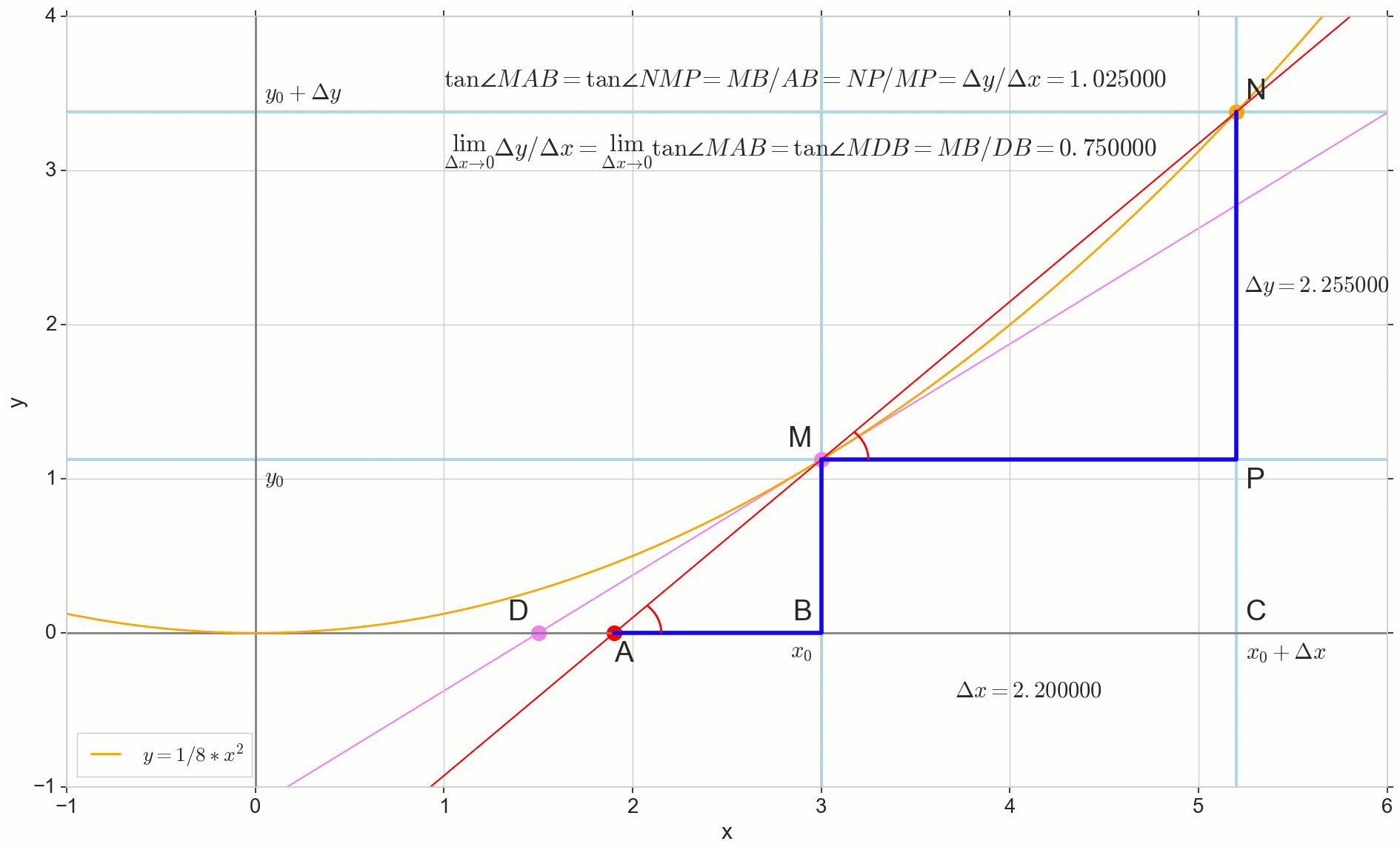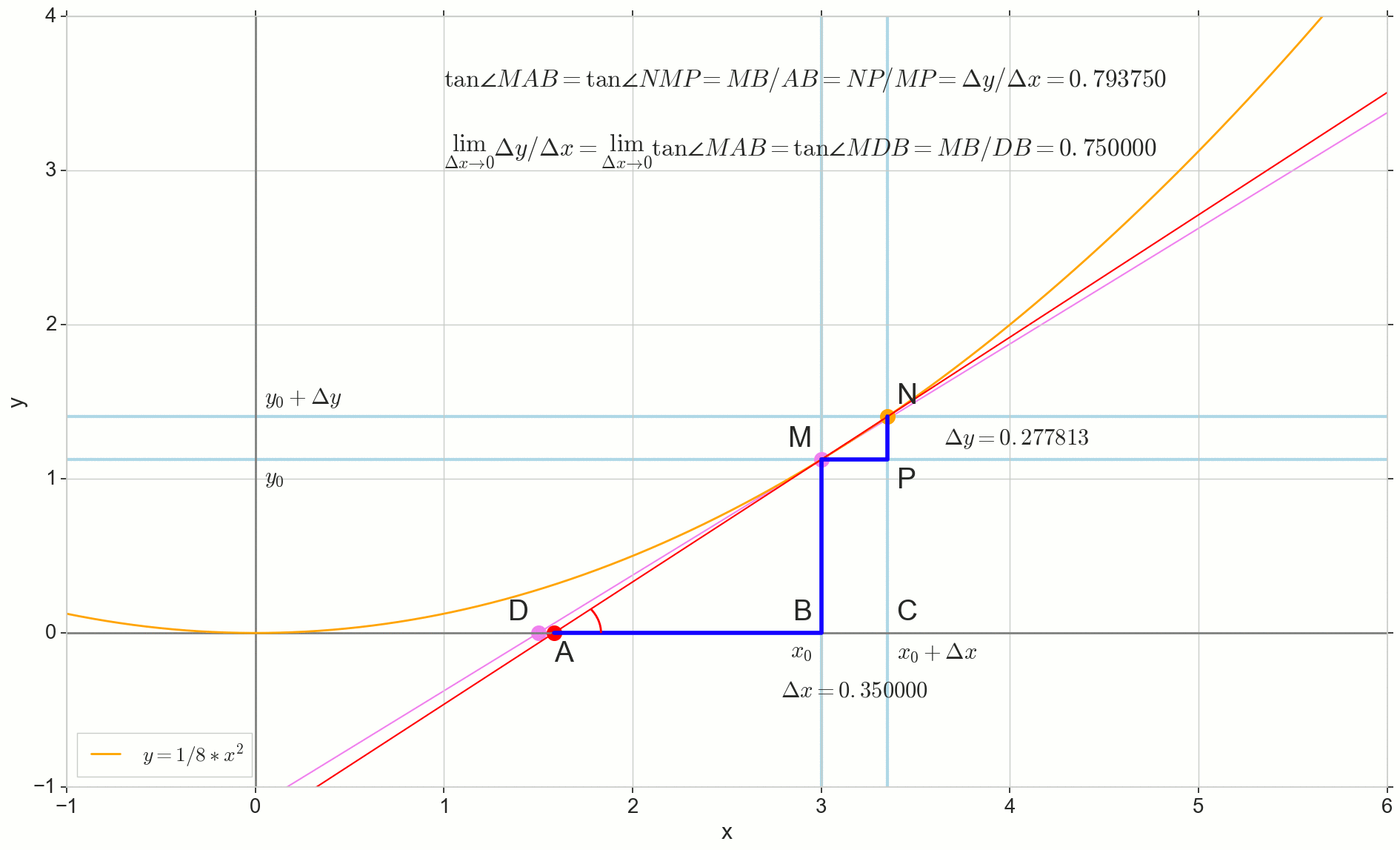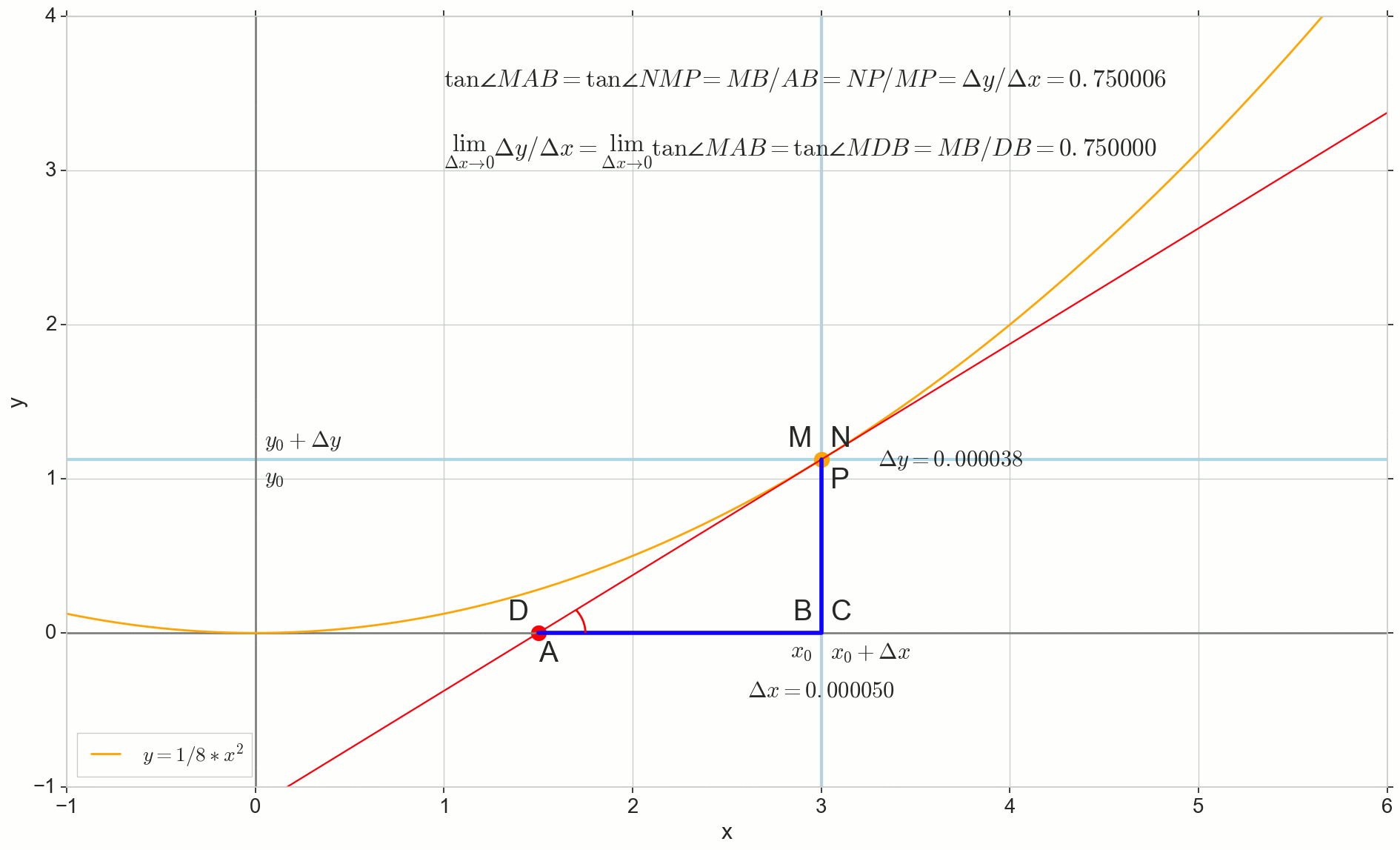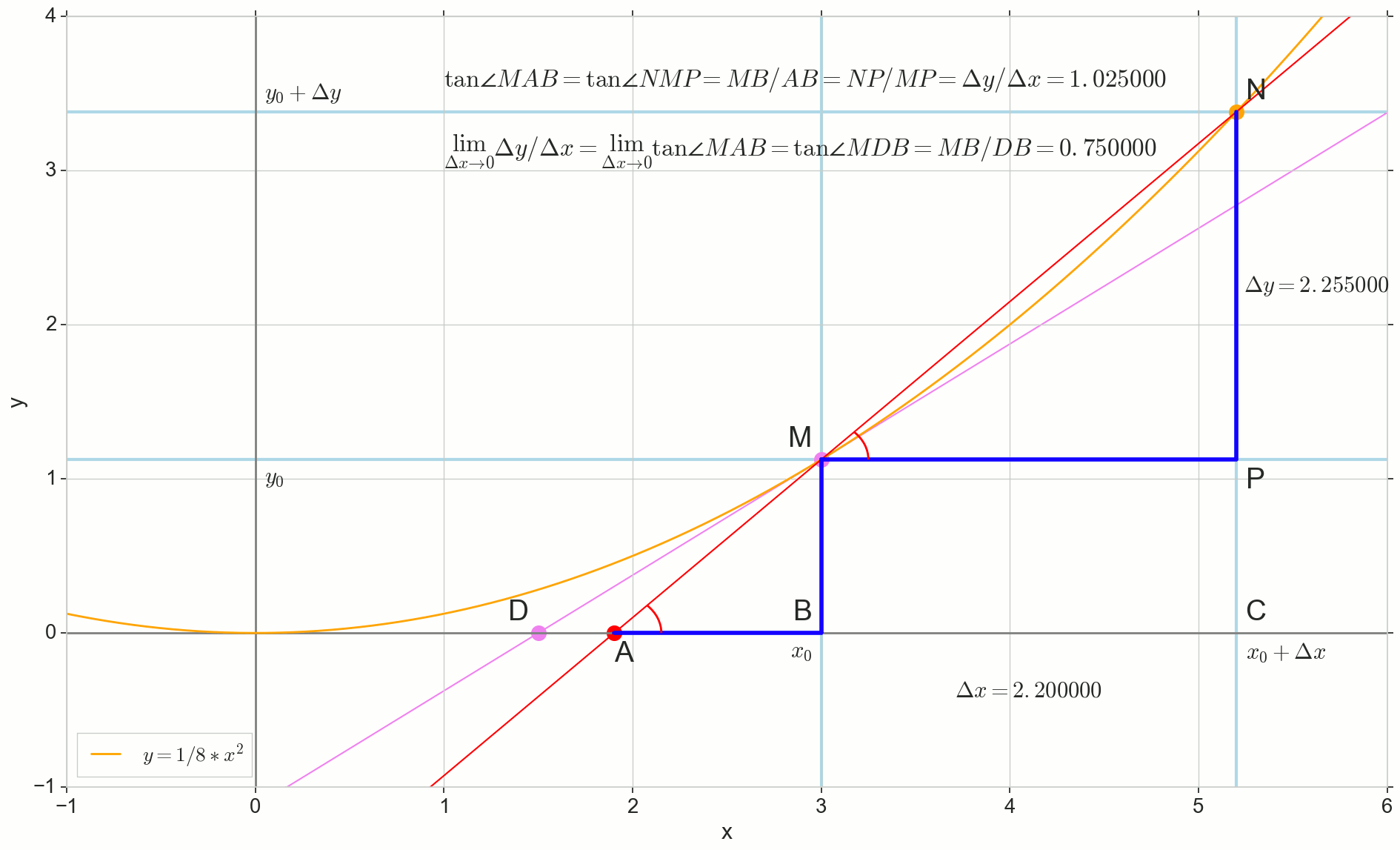
Wie inkrementieren $$$\ Delta x$ , unendlich nahe Null, wird niemals Null erreichen, also der Punkt $$$N$ Komme nie genau an die Stelle $$$M$ Punkt $$$A$ wird den Punkt nicht erreichen $$$D$ Dreieck $$$\ triangle MBA$ wird nicht in $$$\ triangle MBD$ . Glücklicherweise können wir das genaue Ziel für all diese Bewegungen mit dem magischen mathematischen Operator "limit" festlegen. $$$\ lim$ .

$$$\triangle MBA$ — $$$\triangle MBD$ , :

$$

$$\lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \lim_{\Delta x \to 0}{\tan \angle NMP} = \lim_{\Delta x \to 0}{\tan \angle MAB} = \lim_{\Delta x \to 0}{MB \over AB} = {MB \over DB} = \tan \angle MDB$$

:

$$

$$\lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \tan \angle MDB$$

, , :

$$

$$y'(x_0) = \lim_{\Delta x \to 0}{\Delta y \over \Delta x} = \tan \angle MDB$$

, $$$y=0$ . .

, , , , , . , , , , .. ( , , ). : , (, — tangent line , , — ).

:

• $$$x_0$ $$$y=0$
• — $$$y(x_0)$ — $$$x_0$ $$$y=0$ $$$y=0$
• «» , ,
• — : — , —
• ( , , , $$$\Delta y$ )

, , :

— , — $$$x_0$ , — . — — . — $$$y=0$ , — .

, , , , . ( , ) (: $$$y=0$ , ).

( ): , (: $$$y=0$ , ).

, : (), «»/«» , . — . , , ? .

$$$J(w)$ . , , , .

$$

$$J(w)={1 \over 2} SSE ={1 \over 2}\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2}$$

• $$$k$ -
• ,

$$

$$\begin{gathered}\frac{\partial J(w)}{\partial w_{k}} ={\frac{\partial }{\partial w_{k}}}{1 \over 2}\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2} ={1 \over 2}\sum _{i=1}^{n}{\frac{\partial }{\partial w_{k}}}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})^{2} \\={1\over 2}\sum _{i=1}^{n}2(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)}) \frac{\partial }{\partial w_{k}}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)}) \\={1\over 2}2\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)}) \frac{\partial }{\partial w_{k}}((w_{0}x_{0}^{(i)}+...+w_{k}x_{k}^{(i)}+...+w_{m}x_{m}^{(i)}) - y^{(i)}) \\=\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})x_{k}^{(i)} \end{gathered}$$

, : , , , ( ) . , $$$w_k$ ( , ), . , , , $$$1/2$ SSE .

:

$$

$$\begin{gathered}\frac{\partial J(w)}{\partial w_{k}} =\sum _{i=1}^{n}(\sum _{j=0}^{m}w_{j}x_{j}^{(i)} - y^{(i)})x_{k}^{(i)} \end{gathered}$$

— ( $$$\nabla$ [], , .. []):

$$

$$\nabla J(w)=(\frac{\partial J(w)}{\partial w_{0}},...,\frac{\partial J(w)}{\partial w_{m}}), w=(w_{0},...,w_{m})$$

:

$$

$$w:=w+\Delta w, \Delta w=-\eta \nabla J(w)$$

$$$k$ - :

$$

$$w_{k}:=w_{k}+\Delta w_{k}, \Delta w_{k}=-\eta \frac{\partial J(w)}{\partial w_{k}}$$

:

• $$$\eta$ [] — ,

, , , . , .

1- :

$$

$$\Phi(x, w)=w_0+w_1x_1$$

( ):

$$

$$\frac{\partial J(w)}{\partial w_{0}} =\sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})x_{0}^{(i)} =\sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})$$

$$

$$\frac{\partial J(w)}{\partial w_{1}}= \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})x_{1}^{(i)}$$

:

$$

$$\Delta w_{0}=-\eta \frac{\partial J(w)}{\partial w_{0}}=-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})$$

$$

$$\Delta w_{1}=-\eta \frac{\partial J(w)}{\partial w_{1}}=-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}-y^{(i)})x_{1}^{(i)}$$

, . .

( $$$w_1$ )

$$$w_0=1$ , $$$J(w_1)$

$$$X$ ( ) $$$y$ $$$w_0$ und $$$w_1$ ( ):

 def sse_(X, y, w0, w1): return ((w0+w1*X - y)**2).sum() 

$$$w_1$ -1.5 1.5.

  #      w0 = 1 w1 = np.linspace(-1.5, 1.5, 200) #              numpy.dot # https://docs.scipy.org/doc/numpy/reference/generated/numpy.dot.html #    ,      sse = [] for i in range(len(w1)): sse.append(sse_(X1, y, w0, w1[i])) sse = np.array(sse) 

, ( , , ):

  plt.subplot(3,1,1) # sse plt.plot(w1, sse/2, color='red', label='w0=1') #  -   w1_first = .9 plt.scatter(w1_first, sse_(X1, y, w0, w1_first)/2, color='blue', marker='o', s=100) plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'J(w1, w0=1)') plt.legend(loc='lower left') 

, , $$${\delta J(w)} \over {\delta w_1}$ — :

  grad_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() grad_w1.append(grad) plt.subplot(3,1,3) plt.plot(w1, grad_w1, label=u' ∂J(w)/∂w1') plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'∂J(w)/∂w1') plt.legend(loc='upper left') 

$$$\Delta w_1(w_1)$ (, $$$\Delta w_1$ $$$w_1$ , .. , ):

  eta = 0.001 delta_w1 = [] for i in range(len(w1)): grad = ((w0 + w1[i]*X1 - y)*X1).sum() delta = -eta*grad delta_w1.append(delta) plt.subplot(3,1,2) plt.plot(w1, delta_w1, color='orange', label=u'Δw1, η=%s'%eta) plt.xlim(-1.2, 1.2) plt.xlabel(u'w1') plt.ylabel(u'Δw1=-η*∂J(w)/∂w1') plt.legend(loc='upper right') 

  plt.show() 

• : ,
• : — «» ( , «» ),
• : — ( ), $$$\eta$ [] ( ),

: , 1000 .

, ,

$$$w$ — - - . $$$w_0=1$ , $$$w_1=0.9$ . $$$\eta=0.001$ ( , ) 12:

  #    12-14  eta = 0.001 epochs = 12 

:

  #      w1_epochs = [w1_first] delta_w1_epochs = [] w1_next = w1_first for i in range(epochs): grad = ((w0 + w1_next*X1 - y)*X1).sum() delta = -eta*grad w1_next = w1_next + delta delta_w1_epochs.append(delta) w1_epochs.append(w1_next) #   - 0 delta_w1_epochs.append(0) w1_epochs = np.array(w1_epochs) delta_w1_epochs = np.array(delta_w1_epochs) #     sse_epochs = [] for i in range(len(w1_epochs)): sse_epochs.append(sse_(X1, y, w0, w1_epochs[i])) sse_epochs = np.array(sse_epochs) 

$$$w_1$ $$$J(w_1, w_0=1)$ ::

  #     -       size_epochs = [10 + (250-100)*epoch/epochs for epoch in reversed(range(epochs+1))] plt.scatter(w1_epochs, sse_epochs/2, color='blue', marker='o', s=size_epochs, label=u'  , η=%s'%eta) #    w1 plt.plot([w1_epochs, w1_epochs+delta_w1_epochs], [sse_epochs/2, sse_epochs/2], color='orange')#, label='Δw1') 

$$$\Delta w_1(w_1)$

 plt.scatter(w1_epochs, delta_w1_epochs, color='blue', marker='o', s=size_epochs, label=u'  , η=%s'%eta) plt.plot([w1_epochs, w1_epochs], [delta_w1_epochs, np.zeros(len(delta_w1_epochs))], color='orange') 

, , ( ), . , , , .

: , , , «» , — , .

• — $$$w_1$ , —
• , $$$w_1$
• — : , —
• , —
• , ( ), , ( ) — , —
• ( , — ).
• : — , —
• ? — . .
• . $$$w_1$ , . , «»/«» . , , . , , , « ». , : $$$w_1=0.9$ 200, , , , 1. , , , . — $$$\eta$ . , 200 1. $$$\eta=0.001$ , $$$w_1=0.9$ 200*0.001=0.2 ( -1, -0.2) — .
• $$$J(w_1=0.9)=92.43$ , 12 (, ) $$$J(w_1=0.03)=8.54$
• , ,

, . , . , ( , ). $$$\eta$ , .

: , , , .

, , , .

$$$\eta$

• $$$\eta$ [] — ()
• ,
• «»: , , ,
• , $$$J(w)$
• : $$$w_k$ , $$$\eta$ , $$$w_k$

$$$\eta=0.01$

 #    eta = 0.01 epochs = 6 

. , . 3- , 3- , , .. , .. . , , [] .

$$$\eta$ $$$J(w)$ $$$\eta$

  #      J(w0, w1)   w0  w1 #    12-14  eta = 0.001 epochs = 12 #  -   #   w0  w1 -  ,   , #    10-15  # NB: (    , , ,  , #      ) w0_first = -.9 w1_first = -.9 #      w0_epochs = [w0_first] w1_epochs = [w1_first] delta_w0_epochs = [] delta_w1_epochs = [] w0_next = w0_first w1_next = w1_first for i in range(epochs): grad_w0 = (w0_next + w1_next*X1 - y).sum() delta_w0 = -eta*grad_w0 grad_w1 = ((w0_next + w1_next*X1 - y)*X1).sum() delta_w1 = -eta*grad_w1 w0_next = w0_next + delta_w0 w1_next = w1_next + delta_w1 delta_w0_epochs.append(delta_w0) delta_w1_epochs.append(delta_w1) w0_epochs.append(w0_next) w1_epochs.append(w1_next) #     sse_epochs = [] for i in range(len(w1_epochs)): sse = sse_(X1, y, w0_epochs[i], w1_epochs[i]) sse_epochs.append(sse) print('epoch=%d, w0=%f, w1=%f, SSE/2=%f' % (i, w0_epochs[i], w1_epochs[i], sse/2)) sse_epochs = np.array(sse_epochs) #  -      η (--) plt.plot(range(len(sse_epochs)), sse_epochs, label=u'J(w)=SSE/2, η=%s'%eta) plt.xlabel(u'epoch (η=%s)'%eta) plt.ylabel(u'J(w)') plt.legend(loc='upper right') plt.show() 

: , , . , — , , .

:

 #   eta = 0.001 epochs = 50 

:

 #    eta = 0.01 epochs = 8 

.

$$$\eta$ . , , .

, .

:

• : , , ( ). , , , , .
• : .

, ( ) $$$w$ , , . , , , . , , .

,

, .

, :

— :

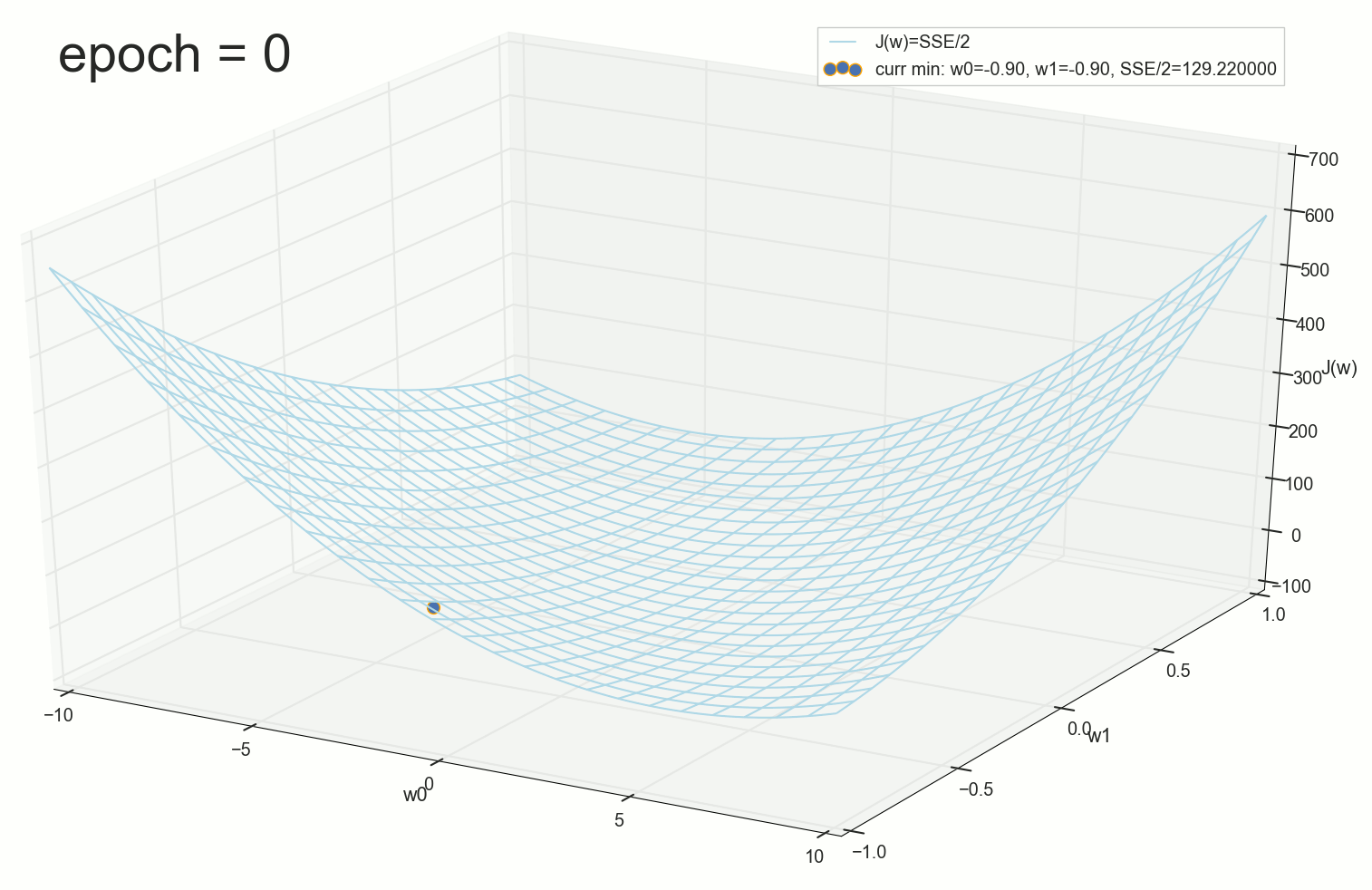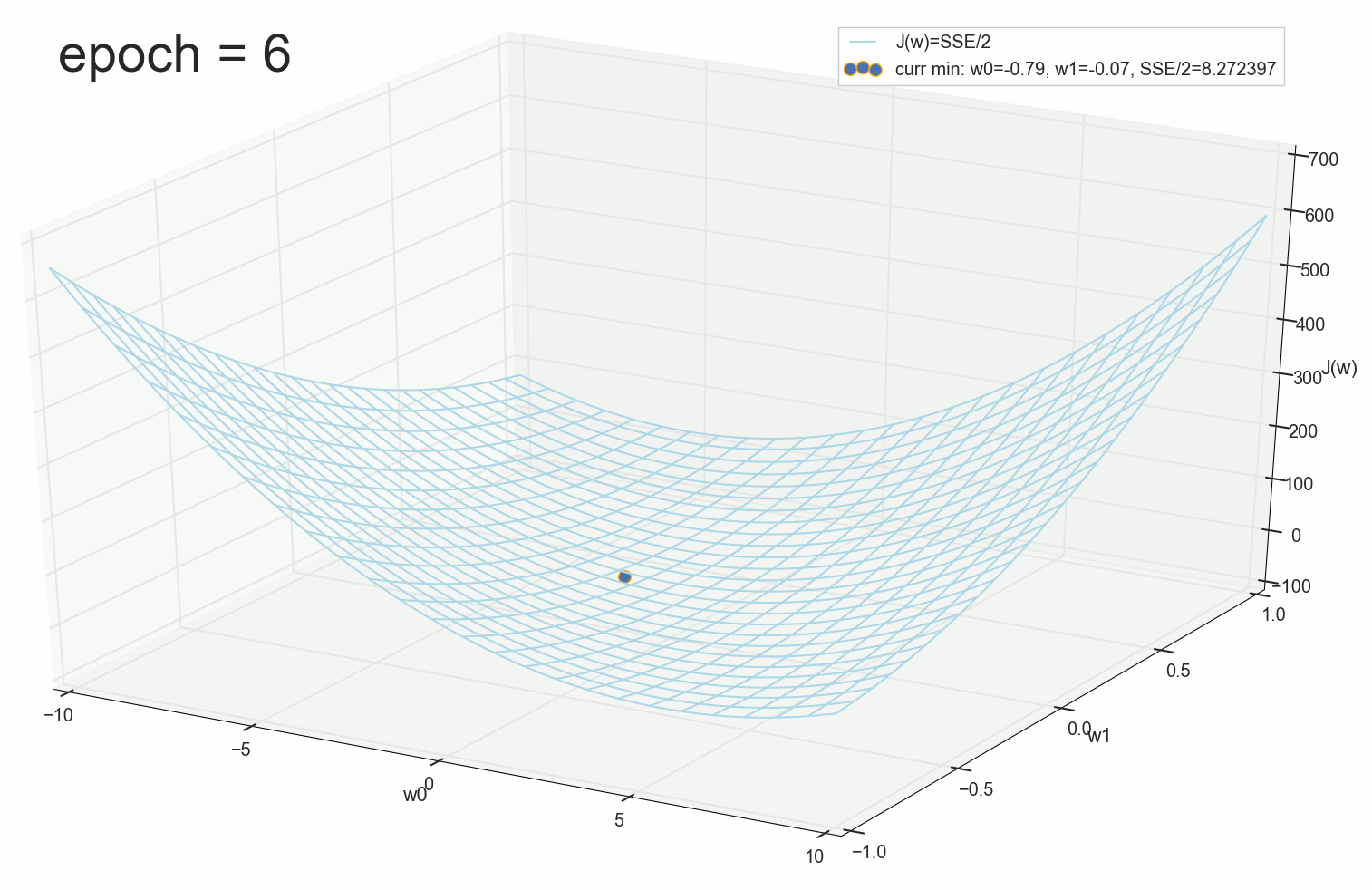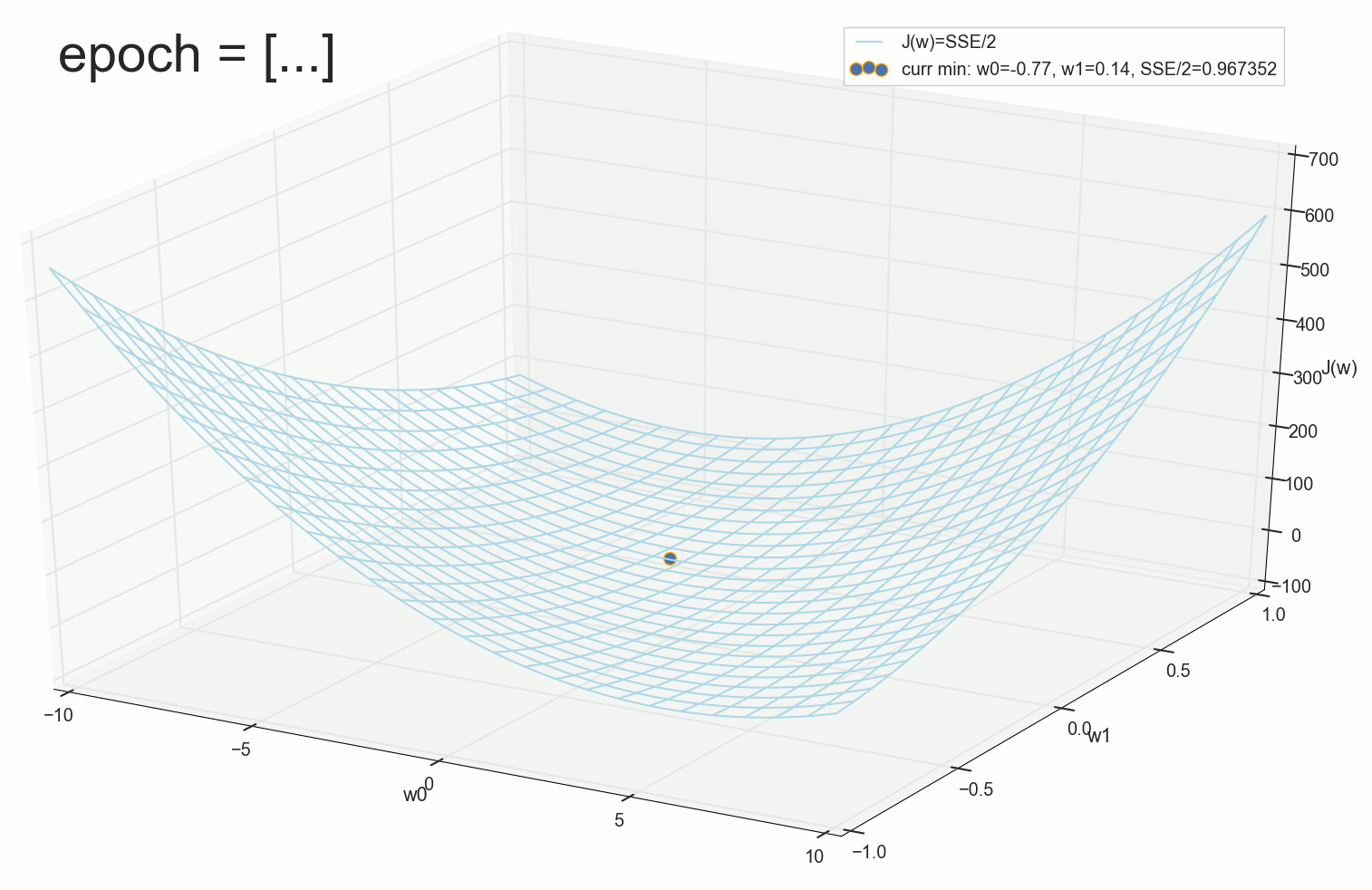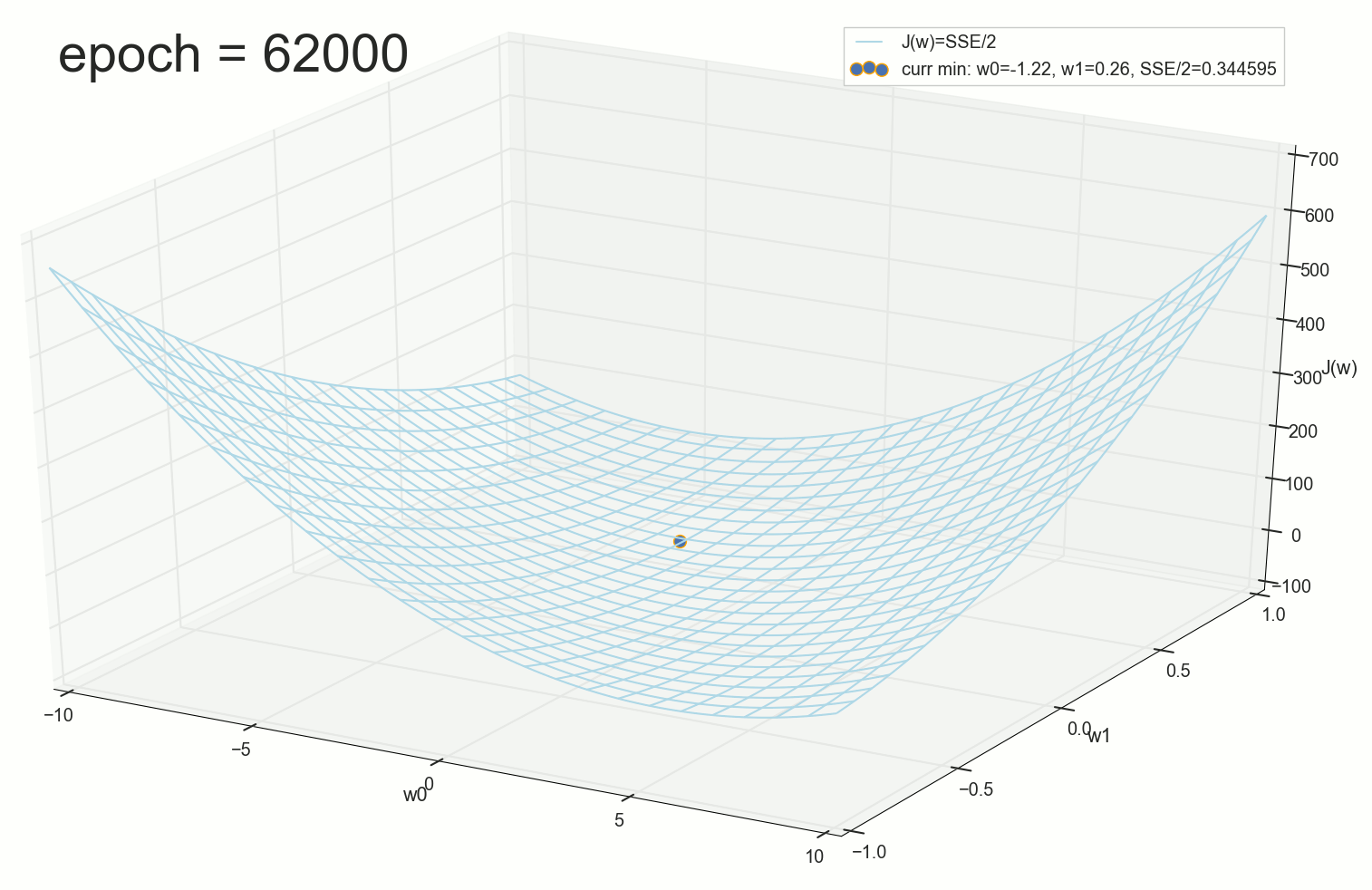
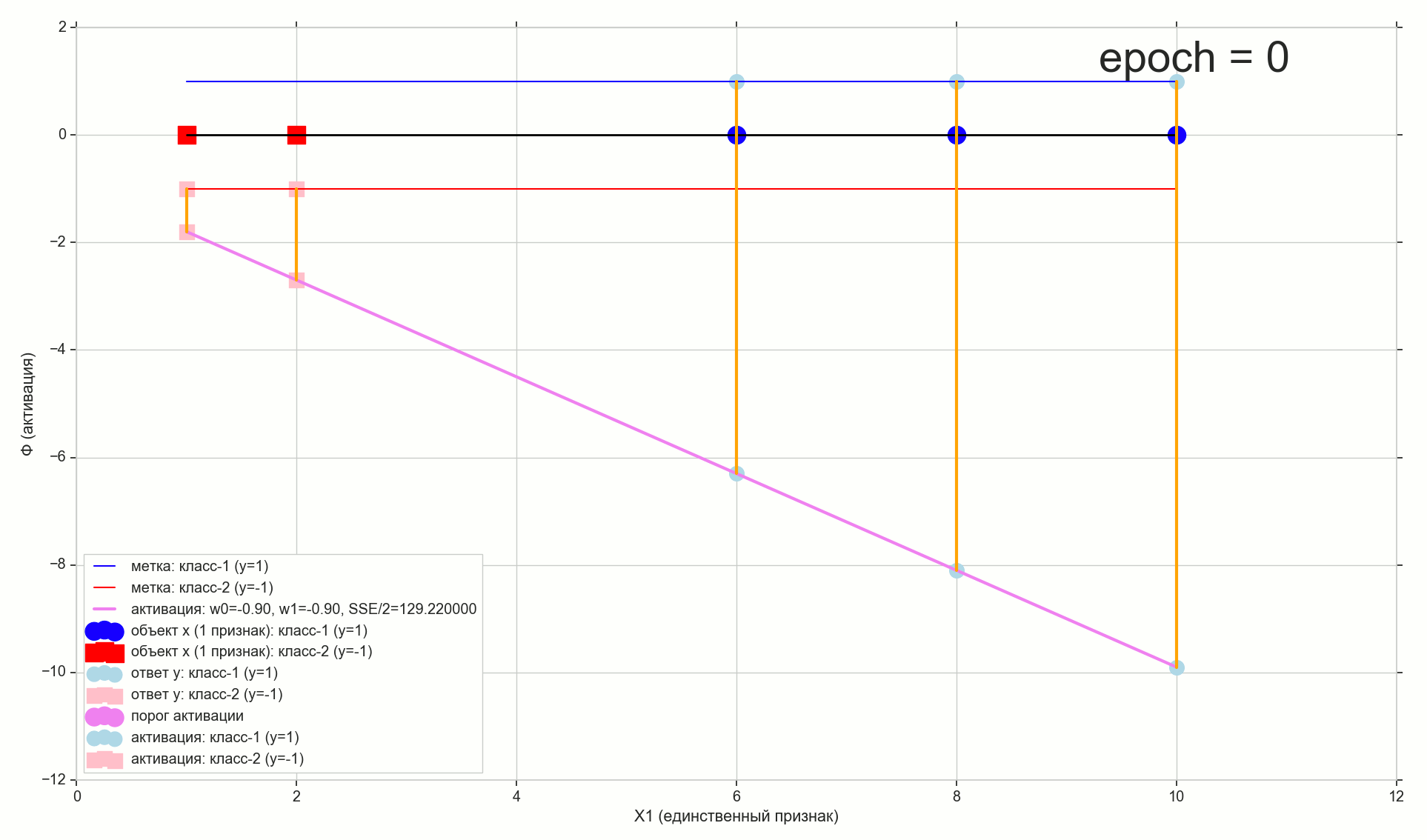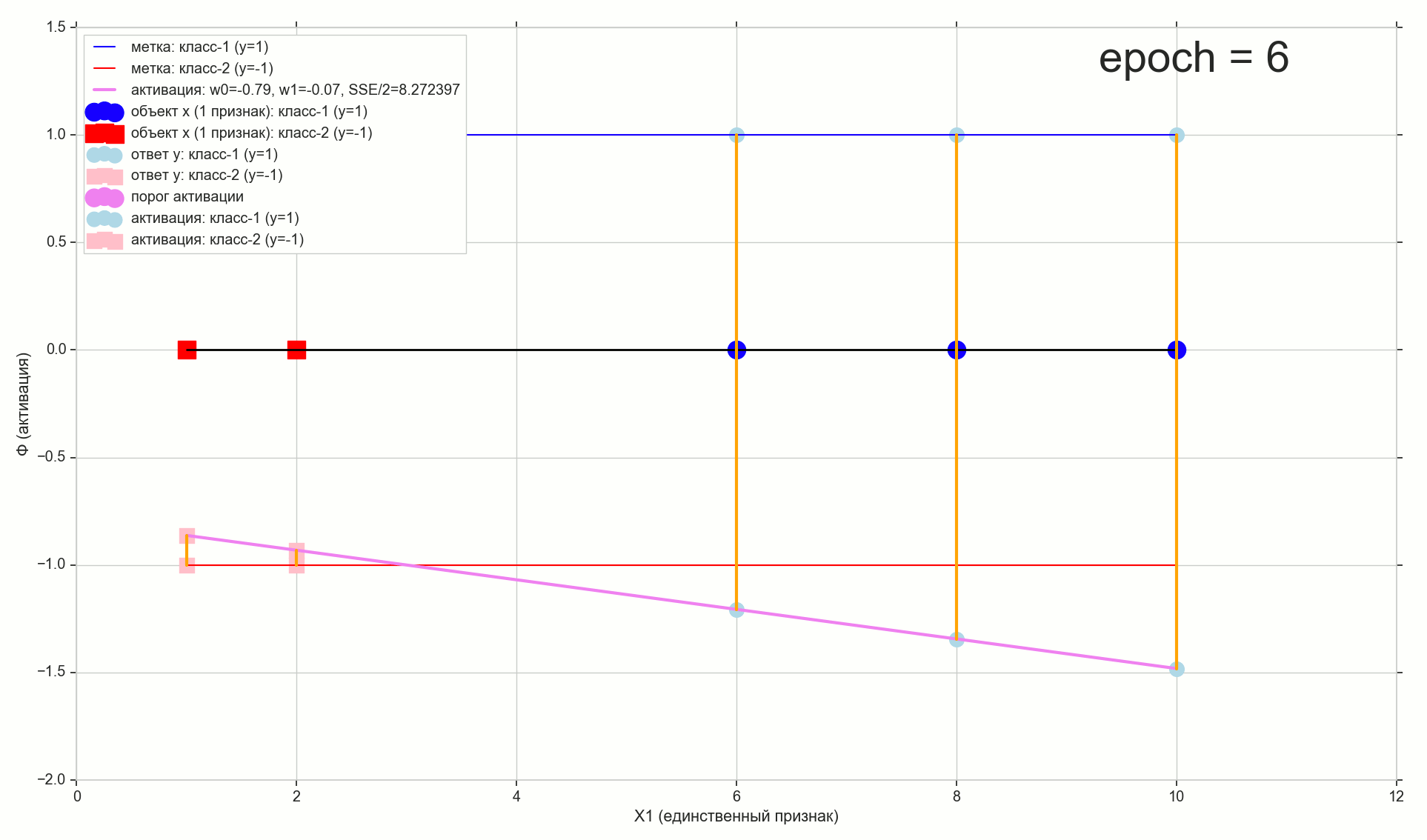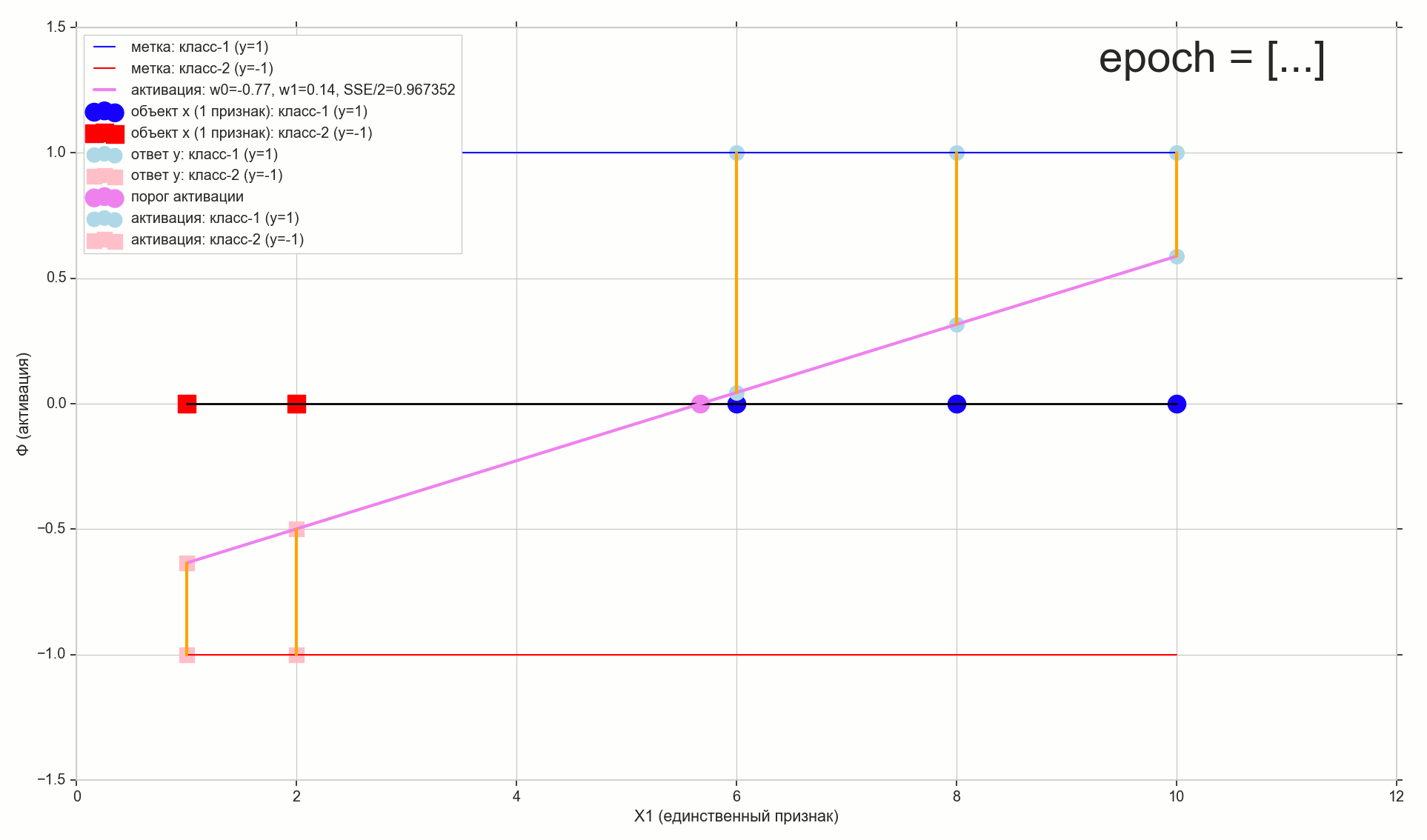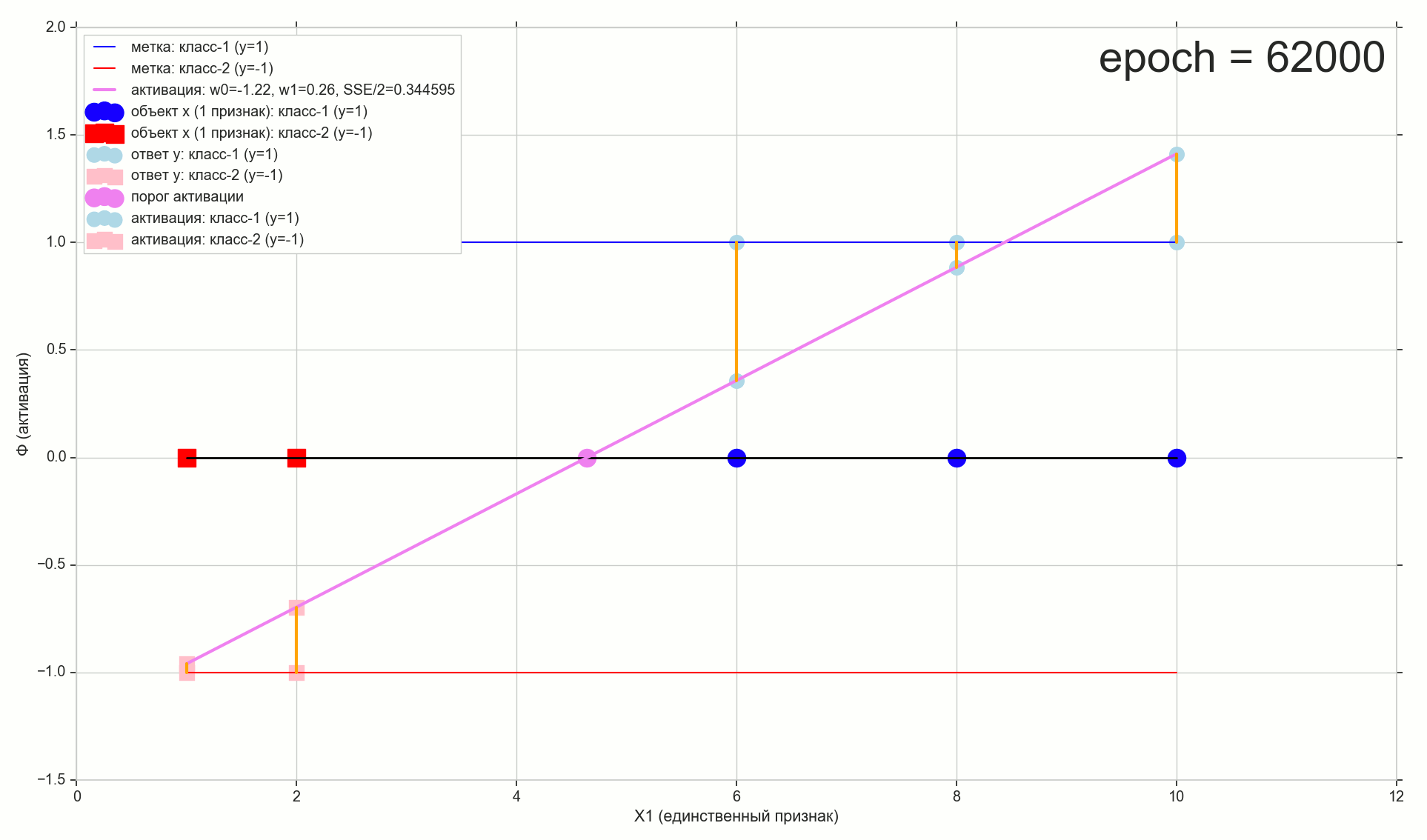
12 — , :

50 :

1767 — , :

, 62000 :

:

. , : , , . , , , , , , . , , - .

, , - , - : , , , , , — . , , , , , , , — . ?

, . :

, , ( ). : , . , , .

. , .

. , , . , — .

— :

11- : , ; :

12- : , , :

50- : , 12-

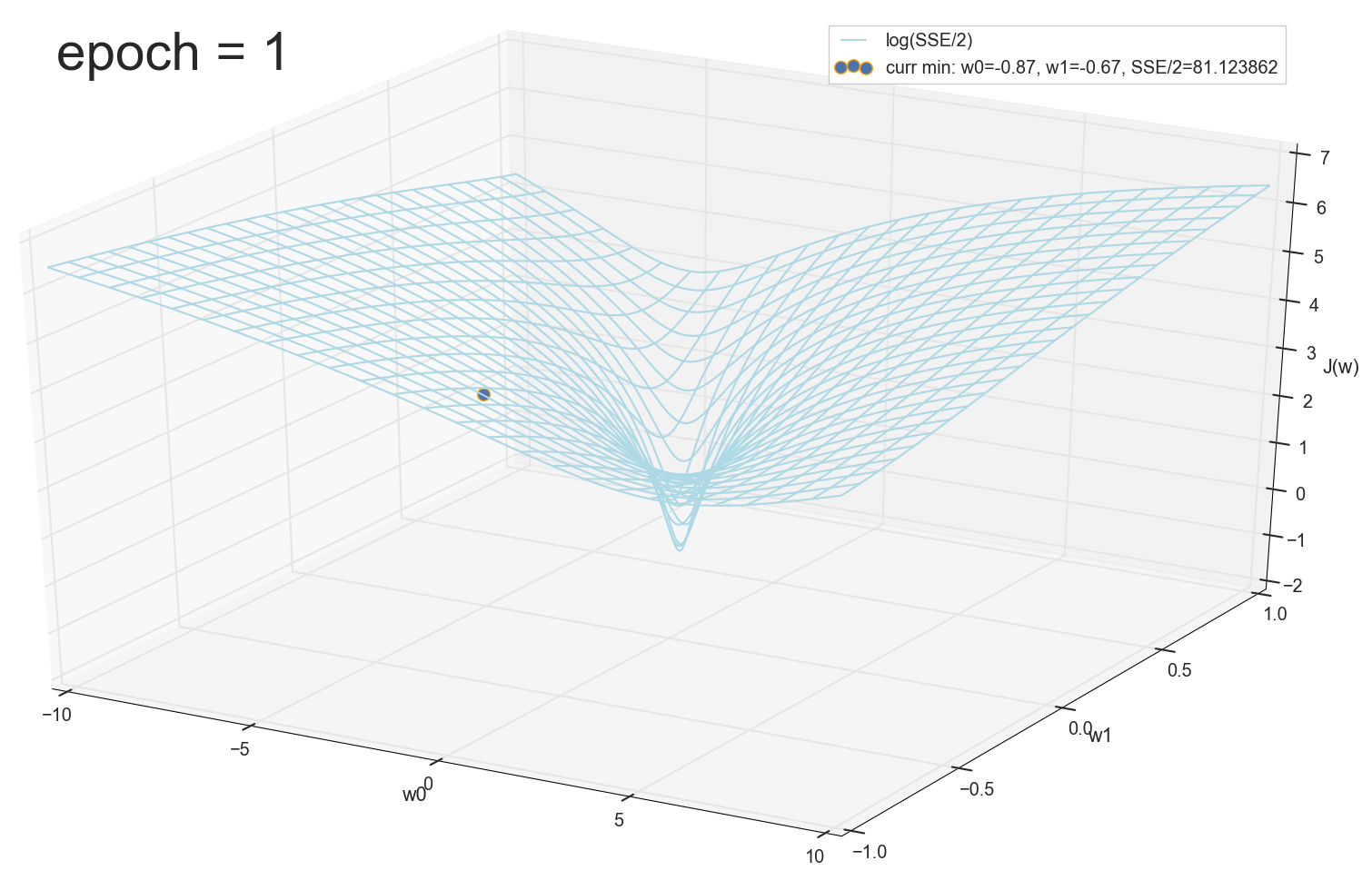
1766: . $$$J(w)=0.3456480221$ — , , ( $$$J(w)=0.3456478372$ : 6- , , )

1767: $$$J(w)=0.34564503$ — , ( 6- , ). $$$w_0=-1.184831$ , $$$w_1=0.258455$ ( $$$w_0$ 2- : $$$w_0=-1.27$ , $$$w_1=0.26$ )

62000: $$$J(w)=0.3445945$ — , ( 2- ). :

:

. , , , , .

• Bei $$$\eta=0.001$ , 10-12- ( )
• , , , (1767)
• — 60
• —

— ( , 1767): $$$w_0=-1.184831$ , $$$w_1=0.258455$ .

.

$$$t^{(1)}=(t_1^{(1)})=(1.4)$ ( , $$$t^{(i)}$ — ). Aber weil , , $$$\hat y=-1$ , .. .

$$

$$SUM=w_0 + w_1*t_1^{(1)} = -1.18 + 0.26*1.4=-0.816$$

$$

$$\Phi(SUM)=SUM=-0.816$$

Quantisierer

$$

$$\Phi(SUM)=-0.816 < 0 \implies \hat y = -1$$

, .

: $$$t^{(2)}=(t_1^{(2)})=(7)$

$$

$$\Phi(SUM)=SUM= -1.18 + 0.26*7 = 0.64 \geqslant 0 \implies \hat y = 1$$

$$$\hat y = 1$ , .. . .

, ( «» ) 12 . , !

(m=2)

, , , . . , , .

— ( ). 2- .

• $$$x = (x_1, x_2)$ ( , , )
• $$$y = \{-1, 1\}$ ( , )

 #  -  ( ) X1 = np.array([2, 3, 1, 5, 10, 1, 6, 7, 10, 6, 7]) X2 = np.array([1, 1, 2, 2, 3, 5, 6, 6, 7, 8, 8]) #   -   y = np.array([-1, -1, -1, -1, 1, -1, 1, 1, 1, 1, 1]) 

 plt.scatter(X1[y == -1], X2[y == -1], s=400, c='red', marker='*', label=u': -1') plt.scatter(X1[y == 1], X2[y == 1], s=200, c='blue', marker='s', label=u': 1') #    #  - -  w0 = -2.7 w1 = .3 w2 = .4 #   ( ) -      =0: # 0=w0+w1*X1+w2*X2 # X2=-(w0+w1*X1)/w2 plt.plot(np.linspace(0,12), -(w0+w1*np.linspace(0,12))/w2, label=u' ') plt.xlim(0, 11) plt.ylim(0, 9) plt.legend(loc='upper left') plt.xlabel('X1') plt.ylabel('X2') plt.show() 

, .

$$

$$\Phi(x, w) = w_0 + w_1 x_1 + w_2 x_2$$

, — , , 1- , 3-:

:

:

— :

() $$$\Phi(w) = 0$ (-). :

, , , , , ( , ). , . , , m=2, (m+1)=3: , — , , — , ( ).

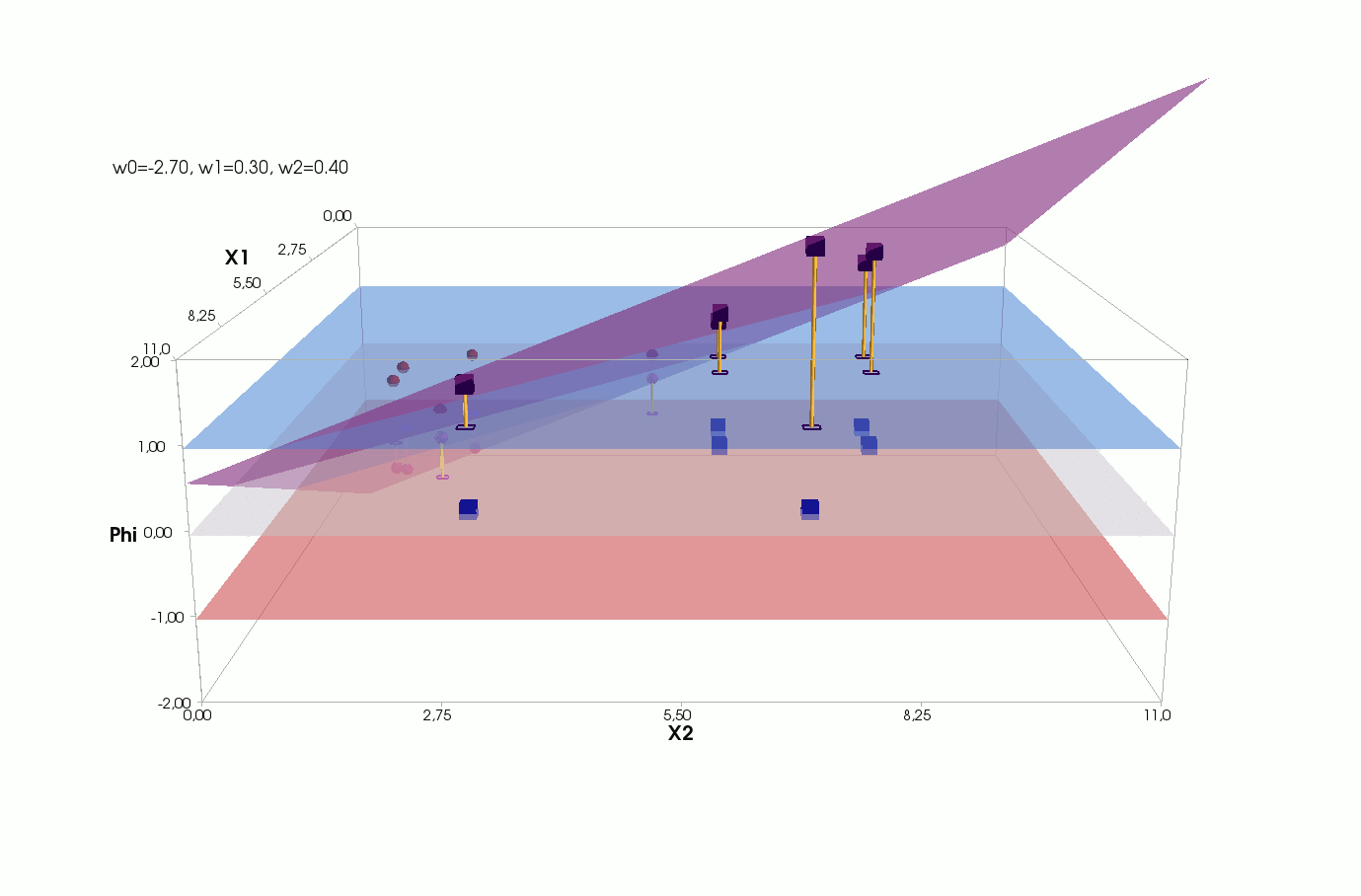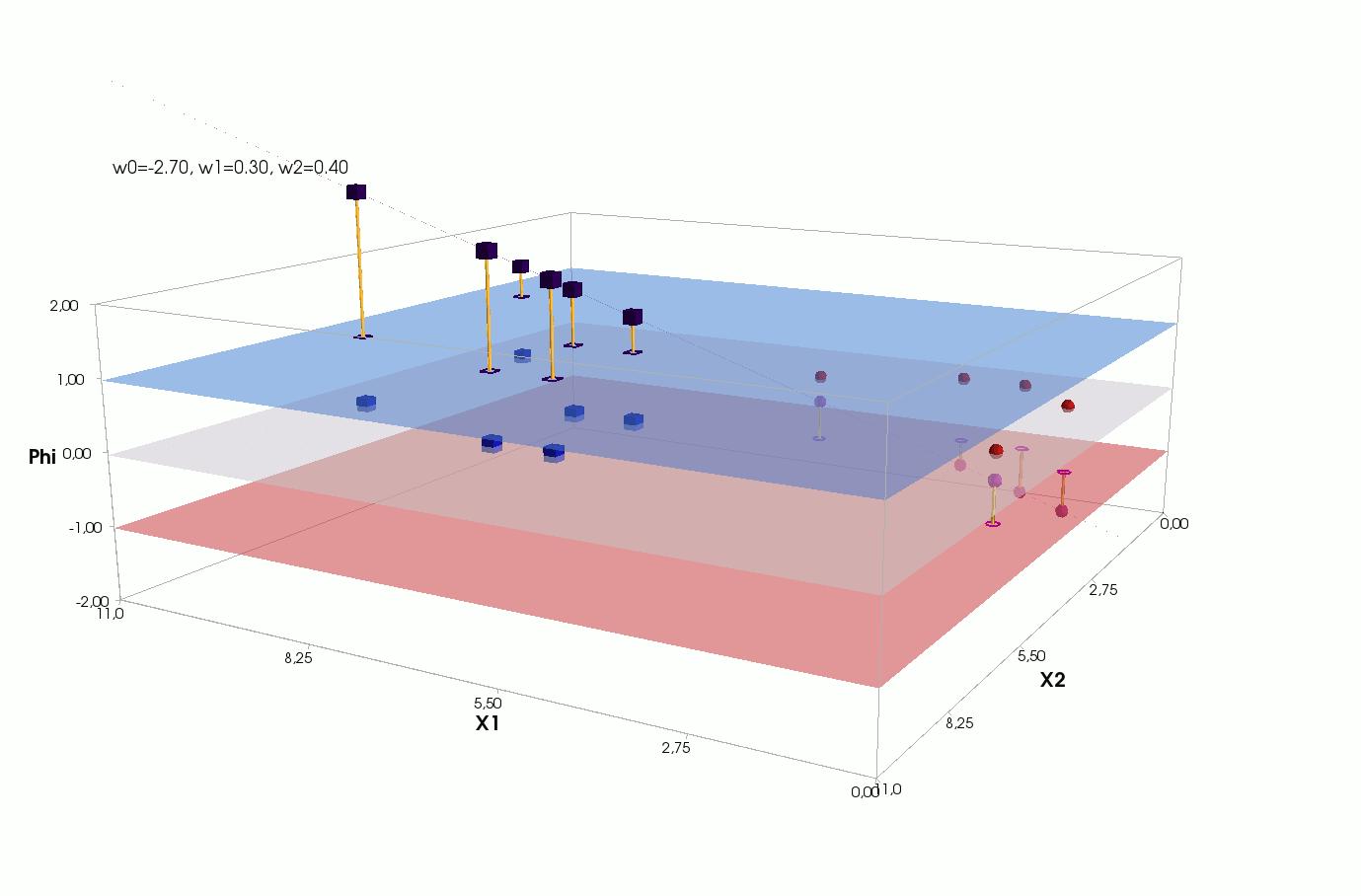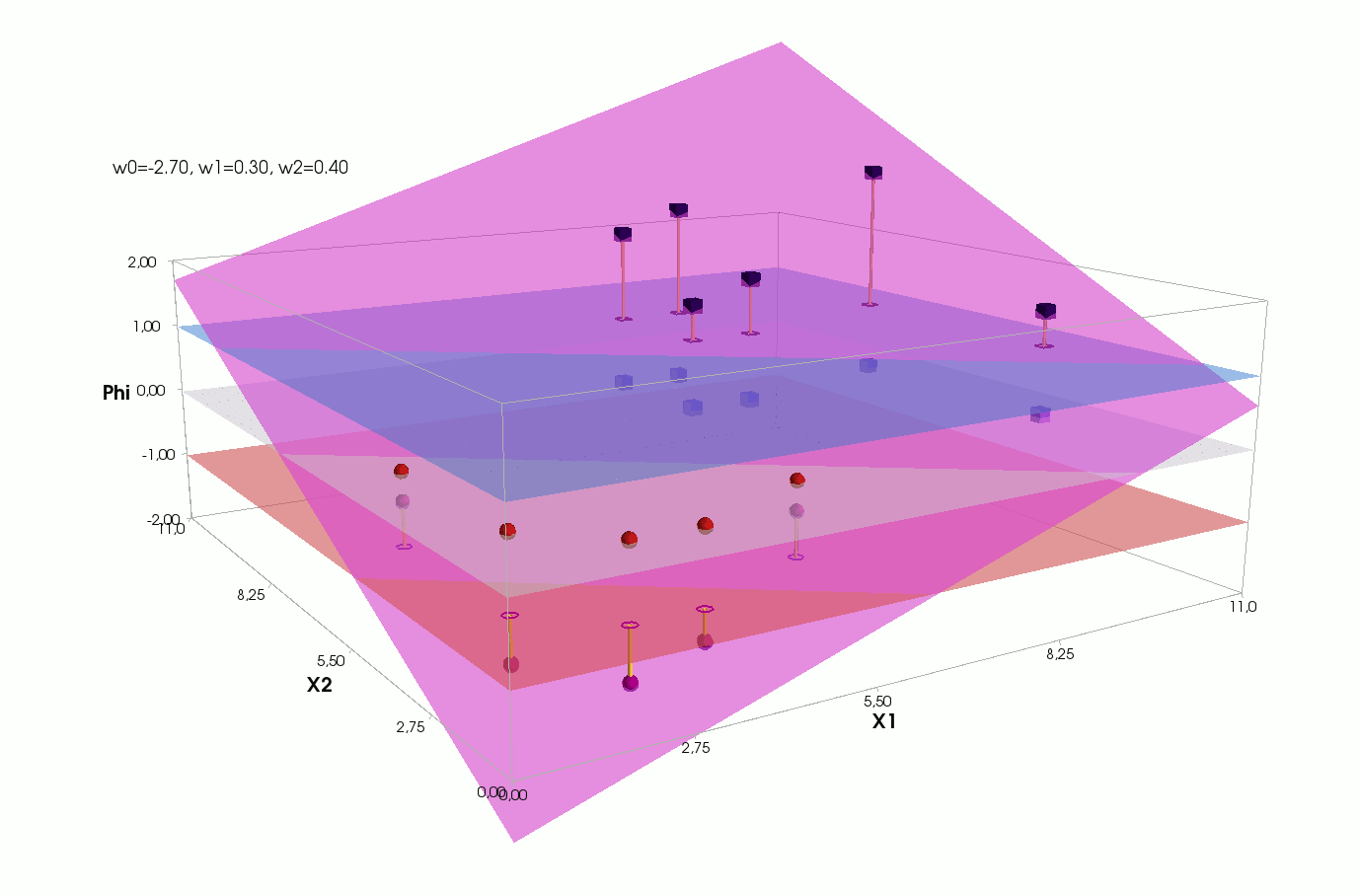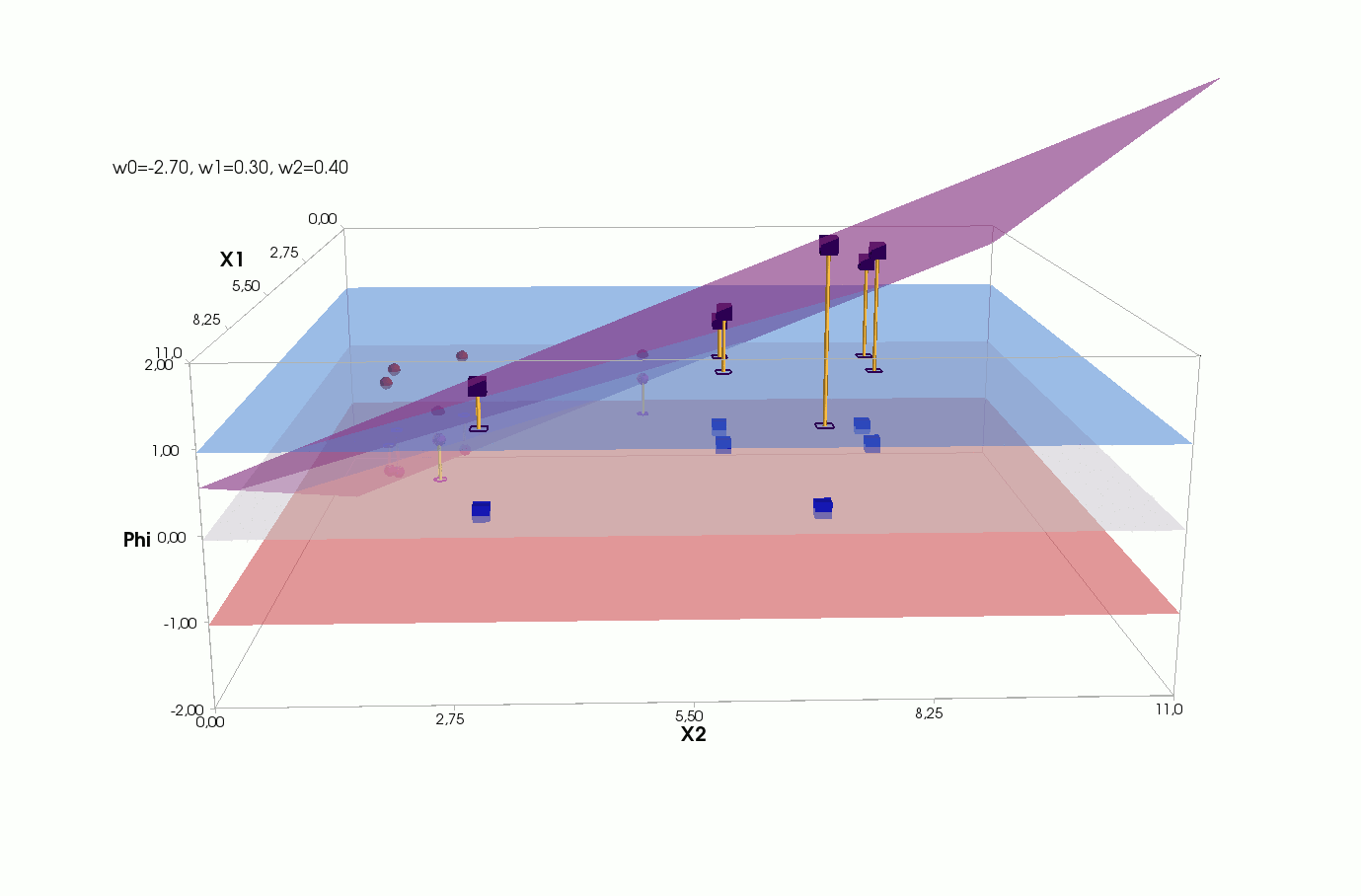
Fehler

$$

$$J(w)={1 \over 2} SSE = {1 \over 2}\sum_{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)} + w_{2}x_{2}^{(i)} - y^{(i)})^{2}$$

() , .., , 3 + — 4 . , 2- 3- - 3-, , - 4- 3-, .

2- . , , 1- 2-.

Farbverlauf

$$

$$\nabla J(w)=(\frac{\partial J(w)}{\partial w_{0}}, \frac{\partial J(w)}{\partial w_{1}}, \frac{\partial J(w)}{\partial w_{1}}), w=(w_{0}, w_{1}, w_{2})$$

( ):

$$

$$\frac{\partial J(w)}{\partial w_{0}} =\sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})$$

$$

$$\frac{\partial J(w)}{\partial w_{1}}= \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{1}^{(i)}$$

$$

$$\frac{\partial J(w)}{\partial w_{2}}= \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{2}^{(i)}$$

:

$$

$$\Delta w_{0}=-\eta \frac{\partial J(w)}{\partial w_{0}} =-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})$$

$$

$$\Delta w_{1}=-\eta \frac{\partial J(w)}{\partial w_{1}} =-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{1}^{(i)}$$

$$

$$\Delta w_{2}=-\eta \frac{\partial J(w)}{\partial w_{2}} =-\eta \sum _{i=1}^{n}(w_{0}+w_{1}x_{1}^{(i)}+w_{2}x_{2}^{(i)}-y^{(i)})x_{2}^{(i)}$$

3- ( 3- ), $$$\eta=0.001$ , $$$w_0=-0.9$ , $$$w_1=-0.9$ , $$$w_2=-0.9$ .

— , , :

:

:

3- - :

4- :

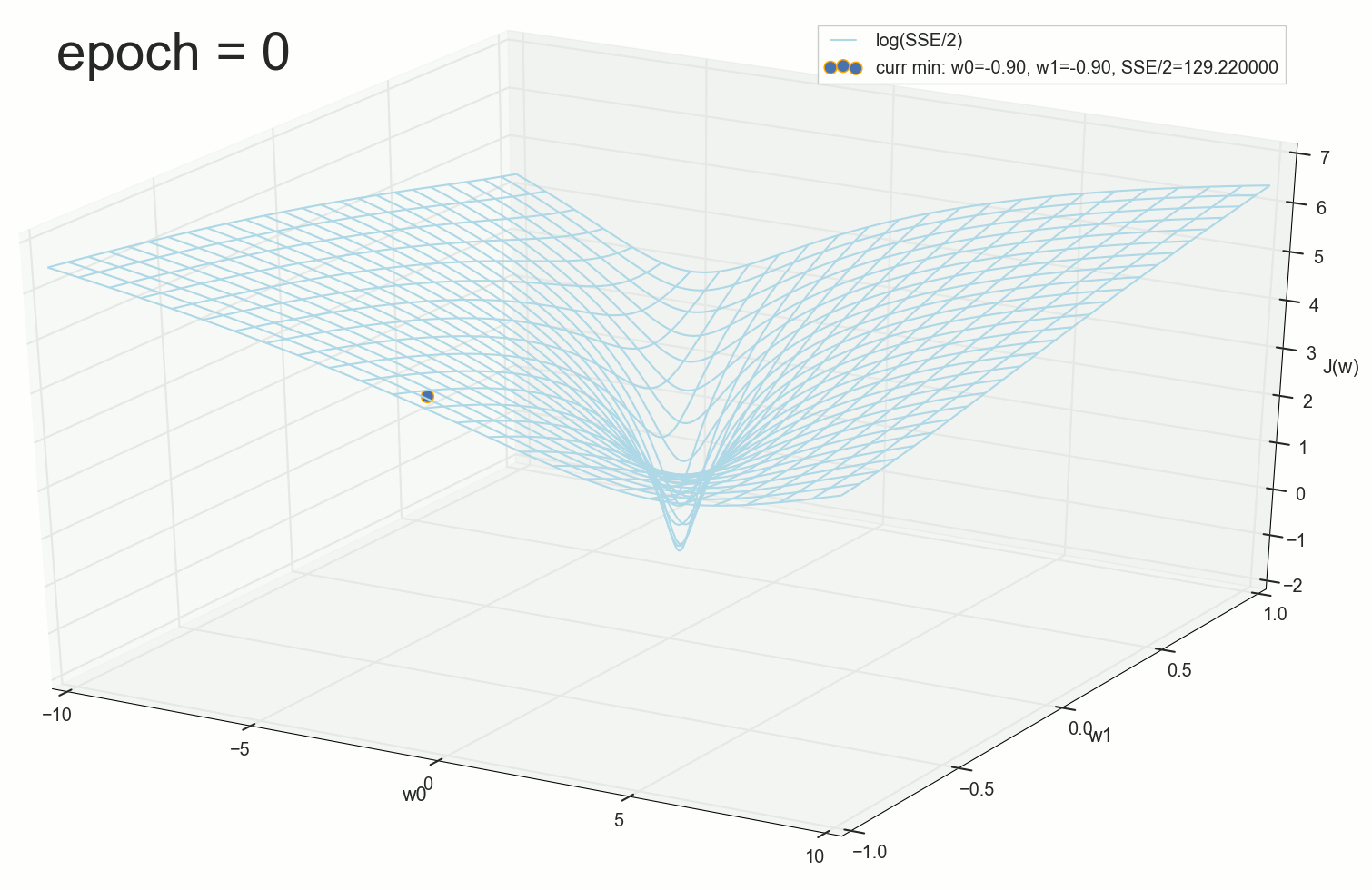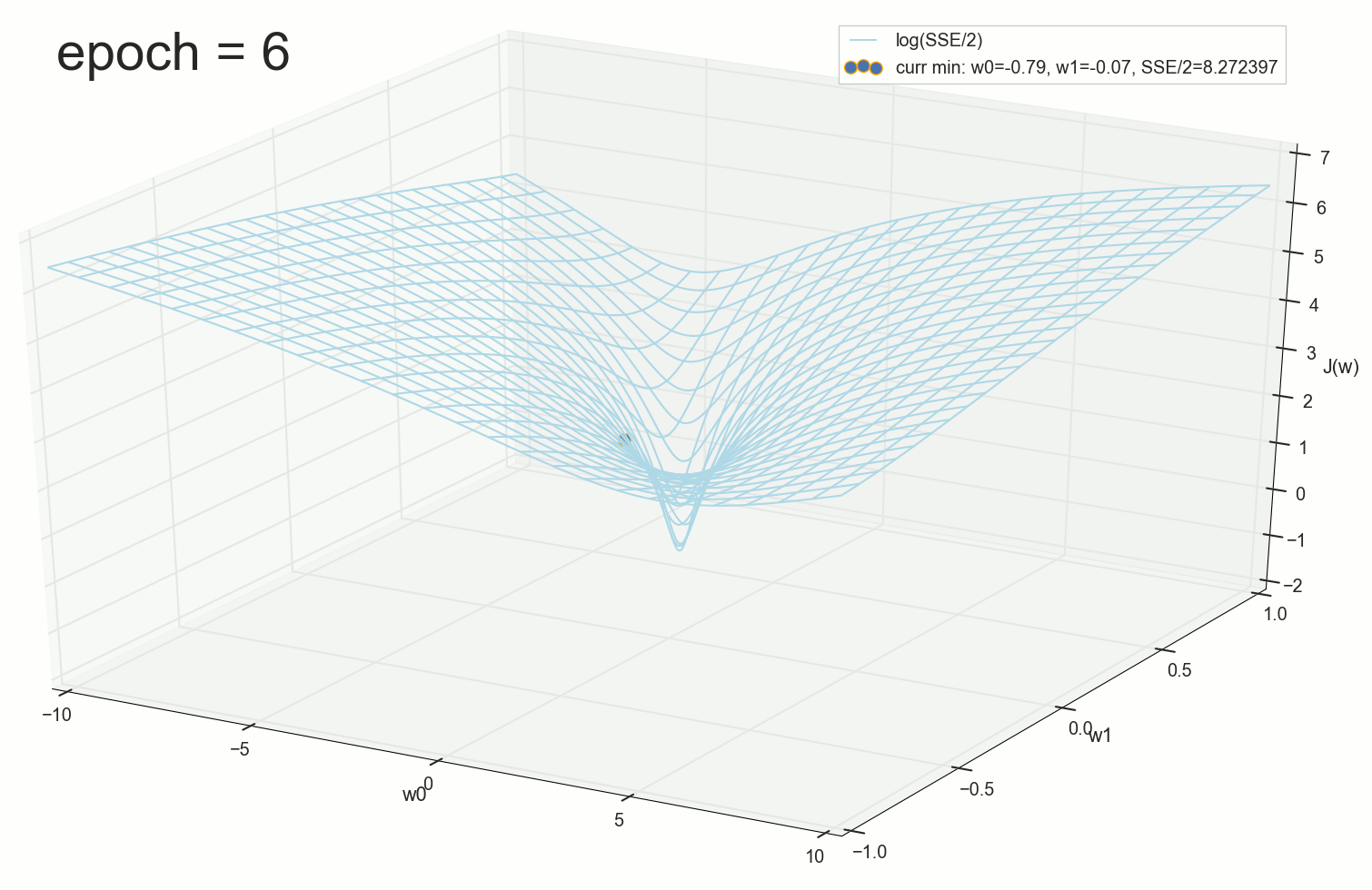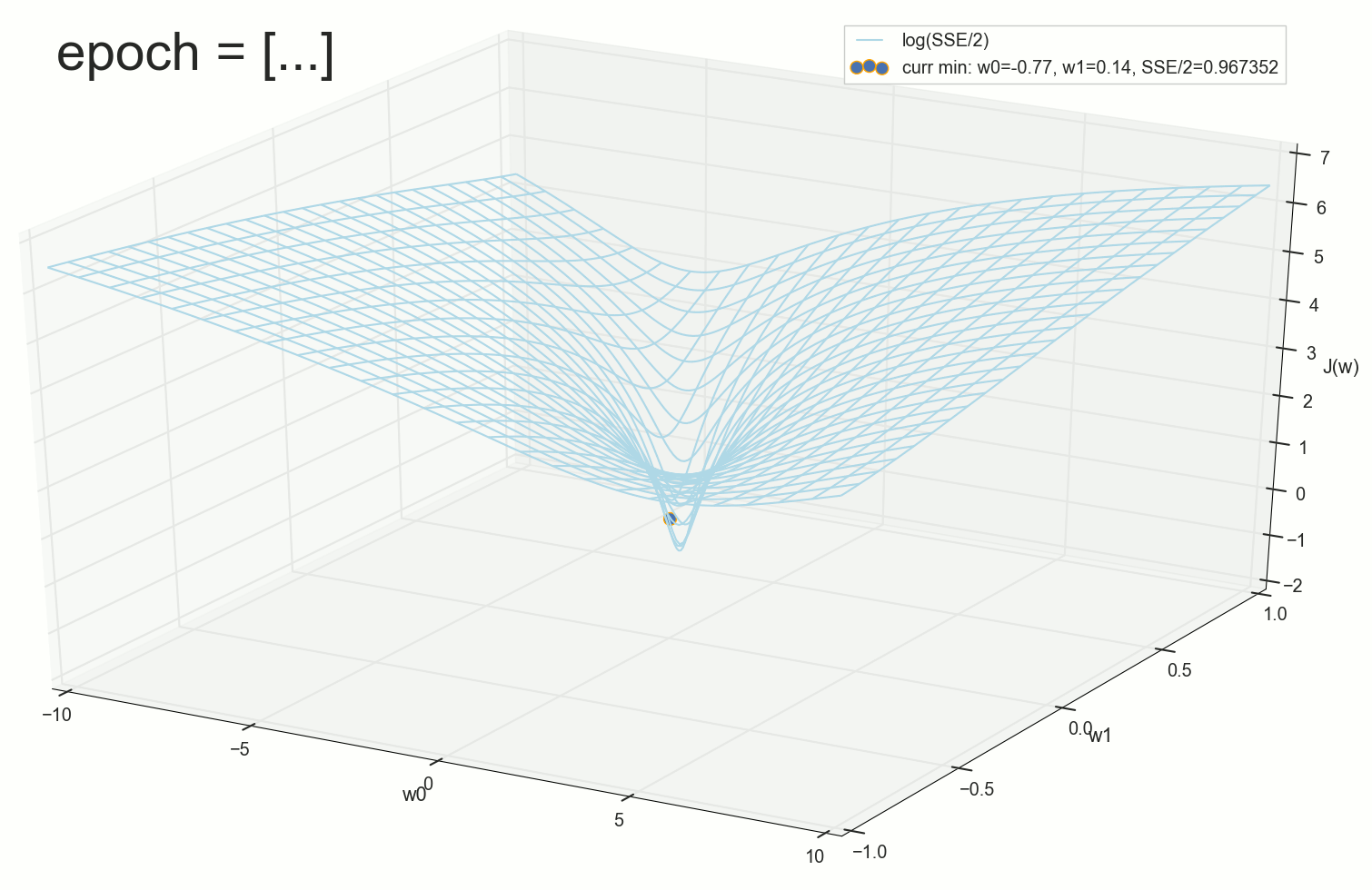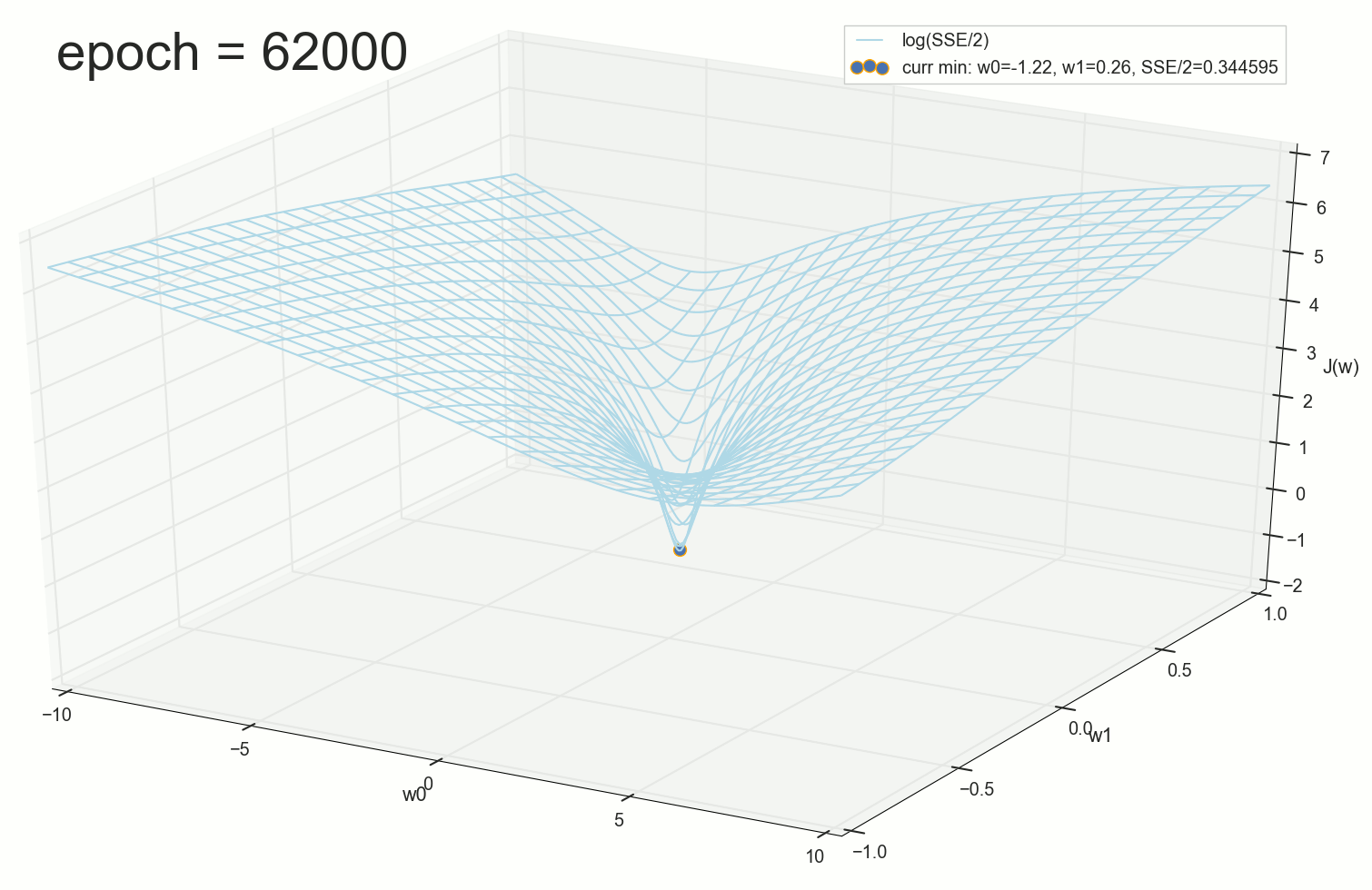
60- — , :

70- , , :

200- — :

400- — :

:

, , $$$w_0$ .

Code

matplotlib ( mpl_toolkits.mplot3d.axis3d) ( , , 3). Mayavi .

 import numpy from mayavi import mlab #    -   mlab.savefig #mlab.options.offscreen = True #   size    mlab.savefig fig = mlab.figure(fgcolor=(10./256., 10./256., 10./256.), bgcolor=(255./256., 255./256., 255./256.), size=(1650, 950)) X1_ = range(0, 12) X2_ = range(0, 12) XX1_, XX2_ = np.mgrid[X1_, X2_] #    # : color=(255./256., 191./256., 71./256.) # : color=(171./256., 0./256., 130./256.) # : color=(255./256., 101./256., 107./256.) # : color=(252./256., 79./256., 245./256.) # : color=(84./256., 148./256., 247./256.) # : color=(45./256., 0./256., 82./256.) # : color=(254./256., 255./256., 87./256.) #  # : color=(.7, .1, .1) # : color=(.1, .1, .7) #   : =1 (y=1), =-1 (y=-1)    =0 mlab.surf(XX1_, XX2_, np.full((12, 12), -1), color=(255./256., 101./256., 107./256.), opacity=0.6) mlab.surf(XX1_, XX2_, np.full((12, 12), 1), color=(84./256., 148./256., 247./256.), opacity=0.5) mlab.surf(XX1_, XX2_, np.full((12, 12), 0), color=(247./256., 243./256., 246./256.), opacity=0.5) #     # (   , ..      ,   #     :    2- , 3  - #   ,   ) mlab.points3d(X1[y == -1], X2[y == -1], np.full(X1[y == -1].size, 0), color=(.7, .1, .1), mode='sphere', scale_factor=.2) mlab.points3d(X1[y == 1], X2[y == 1], np.full(X1[y == 1].size, 0), color=(.1, .1, .7), mode='cube', scale_factor=.2) #     mlab.points3d(X1[y == -1], X2[y == -1], np.full(X1[y == -1].size, -1), color=(171./256., 0./256., 130./256.), mode='2dcircle', scale_factor=.2) mlab.points3d(X1[y == 1], X2[y == 1], np.full(X1[y == 1].size, 1), color=(45./256., 0./256., 82./256.), mode='2dsquare', scale_factor=.2) #    #      # ... epoch=12 w0=-0.762718 w1=0.165023 w2=0.040271 sse=3.598883 #  -   y=w0+w1*X1+w2*X2 yy_ = w0 + w1*XX1_ + w2*XX2_ actsurf = mlab.surf(XX1_, XX2_, yy_, color=(252./256., 79./256., 245./256.), opacity = 0.6) #       y_ = w0 + w1*X1 + w2*X2 mlab.points3d(X1[y==-1], X2[y==-1], y_[y==-1], color=(171./256., 0./256., 130./256.), mode='sphere', scale_factor=.2) mlab.points3d(X1[y==1], X2[y==1], y_[y==1], color=(45./256., 0./256., 82./256.), mode='cube', scale_factor=.2) #   -       #      for i in range(len(X1[y==-1])): mlab.plot3d( [X1[y==-1][i], X1[y==-1][i]], [X2[y==-1][i], X2[y==-1][i]], [y[y==-1][i], y_[y==-1][i]], color=(255./256., 191./256., 71./256.)) for i in range(len(X1[y==1])): mlab.plot3d( [X1[y==1][i], X1[y==1][i]], [X2[y==1][i], X2[y==1][i]], [y[y==1][i], y_[y==1][i]], color=(255./256., 191./256., 71./256.)) #   -       # (      ) zmin=-2. zmax=2. vis_area = mlab.points3d( [np.min(X1_), np.max(X1_)], [np.min(X2_), np.max(X2_)], [zmin, zmax], mode='point') #          mlab.view( focalpoint=((np.max(X1_)-np.min(X1_))/2, (np.max(X2_)-np.min(X2_))/2, (zmax-zmin)/2), distance=25, azimuth=-50, elevation=75) mlab.move((0,0,10)) #           fig.scene.renderer.use_depth_peeling = 1 #  mlab.outline(vis_area, color=(.7, .7, .7)) #   ,      : -2, -1, 0, 1, 2 axes = mlab.axes(vis_area, nb_labels=5, color=(.7, .7, .7), ranges=[np.min(X1_), np.max(X1_), np.min(X2_), np.max(X2_), zmin, zmax], #xlabel=u'X1', ylabel=u'X2', zlabel=u'(SUM) - ') xlabel=u'X1', ylabel=u'X2', zlabel=u'Phi') #      #from pprint import pprint #pprint(vars(axes)) axes._label_text_property.bold = False axes._label_text_property.italic = False axes._title_text_property.bold = True axes._title_text_property.italic = False #  ,     #axes._title_text_property.font_size = 34 #         : axes.axes.font_factor = .7 #       size  mlab.figure, #        title = mlab.title("epoch=" + str(epoch)) title.actor.text_scale_mode='none' title.property.justification='right' title.property.font_size=48 legend = mlab.text(.6, .8, 'w0=%0.2f, w1=%0.2f, w2=%0.2f, sse/2=%0.6f'%(w0, w1, w2, sse/2)) legend.actor.text_scale_mode='none' legend.property.font_size=18 #   mlab.show() #    #mlab.savefig("epoch" + str(epoch) + ".png") #    :     ,    # (    , , ,  , #    ,     ) #mlab.clf() #mlab.close() #    -      ''' fpoint = ( (np.max(X1_)-np.min(X1_))/2, (np.max(X2_)-np.min(X2_))/2, (zmax-zmin)/2 ) for i in range (0, 360, 2): mlab.view(focalpoint=fpoint, distance=25, elevation=75, azimuth=i) mlab.move((0,0,10)) mlab.savefig("act-2d-azimuth" + str(i) + ".png") ''' 

, Mayavi , . , , , .

Mayavi, Matplotlib/axes3d, 3- OpenGL. , ( ) , Qt. mayavi . pip PyQt5 python-qt (, - , 'qt'). , , , , , :

 env QT_API=pyqt python3 gradient-2d.py 

— $$$J(w)$

 def sse_(X1, X2, y, w0, w1, w2): return ((w0+w1*X1+w2*X2 - y)**2).sum() #      J(w0, w1, w2) #   w0, w1  w2 #   eta = 0.001 #      () epochs = 70 w0_first = -.9 w1_first = -.9 w2_first = -.9 #      w0_epochs = [w0_first] w1_epochs = [w1_first] w2_epochs = [w2_first] delta_w0_epochs = [] delta_w1_epochs = [] delta_w2_epochs = [] w0_next = w0_first w1_next = w1_first w2_next = w2_first for i in range(epochs): grad_w0 = (w0_next + w1_next*X1 + w2_next*X2 - y).sum() delta_w0 = -eta*grad_w0 grad_w1 = ((w0_next + w1_next*X1 + w2_next*X2 - y)*X1).sum() delta_w1 = -eta*grad_w1 grad_w2 = ((w0_next + w1_next*X1 + w2_next*X2 - y)*X2).sum() delta_w2 = -eta*grad_w2 w0_next = w0_next + delta_w0 w1_next = w1_next + delta_w1 w2_next = w2_next + delta_w2 delta_w0_epochs.append(delta_w0) delta_w1_epochs.append(delta_w1) delta_w2_epochs.append(delta_w2) w0_epochs.append(w0_next) w1_epochs.append(w1_next) w2_epochs.append(w2_next) #     sse_epochs = [] for i in range(len(w1_epochs)): sse = sse_(X1, X2, y, w0_epochs[i], w1_epochs[i], w2_epochs[i]) sse_epochs.append(sse) #print('epoch=%d, w0=%f, w1=%f, w2=%f, SSE=%f, SSE/2=%f' % # (i, w0_epochs[i], w1_epochs[i], w2_epochs[i], sse, sse/2)) sse_epochs = np.array(sse_epochs) #  -      η (--) plt.plot(range(len(sse_epochs)), sse_epochs, label=u'J(w)=SSE/2, η=%s'%eta) plt.xlabel(u'epoch (η=%s)'%eta) plt.ylabel(u'J(w)') plt.legend(loc='upper right') plt.show() 

12 :

70 :

, , : 6-12- , 70- — 70- , 30-, 40- 200-, , , , .

Fazit

ADALINE (adaptive linear neuron — ) — . scikit-learn ADALINE ( - , ) , , - « 80-» (ADALINE 60-), .

«Python » ( scikit-learn) , - .

ADALINE .

-, — , : , , , .

-, () , , , ( , , $$$y$ ) — , scikit-learn.

PS , ADALINE . , , , , ADALINE - , . , ADALINE . , - .