In der vorherigen
Serie haben wir Bruchzahlen untersucht, die keine rationalen Zahlen enthielten. Heute wartet genau dieser nicht als Teil betrachtete Teil auf uns, und wir werden uns auch auf einen etwas komplizierteren letzten Teil vorbereiten, ohne Begriffe wie Restklassenringe oder Modulo-Vergleiche mit diskretem Logarithmus zu verwenden. Auch im dritten Teil der Interessenten warten Preise in Höhe von 400.000 US-Dollar. Warum im dritten? Denn ohne eine Einführung in das Thema ist es nicht immer leicht zu verstehen, warum Preise nicht so leicht zu bekommen sind. Und nach dem Lesen - nur Glück und eine zielgerichtete, geduldige, aber nicht sehr schwierige Aktivität - das ist alles, was Sie brauchen.
Rationale Sterne
Um die zuvor gestellten Fragen zu rationalen Zahlen zu beantworten, benötigen wir erneut einen kleinen Exkurs. Denken Sie zunächst daran, dass wir beim Teilen durch die „Ecke“ ständig den Rest erhalten, indem wir einen bestimmten Teil der Dividendenzahl durch den Teiler teilen. In diesem Fall wird der gesamte Teil der Division in das Ergebnis geschrieben, und der Rest der Division wird mit der Basis des Zahlensystems multipliziert. Danach wird der Divisionsvorgang mit dem Rest wiederholt, bis die Periode erkannt wird oder alle Faktoren des Divisors reduziert sind und wir den endgültigen Bruch erhalten.
Es sieht so aus:
5 | 3 ------ 1.66(6) 3 20 18 20 18 2 ...
Hier ist der Rest der Subtraktion von 18 von 20 immer gleich zwei, die wir dann mit der Basis des Dezimalzahlensystems multiplizieren.
Lassen Sie uns nun überlegen, wie sich die Division von 5 durch 3 beispielsweise von der Division von 1 durch 3 unterscheidet. Die Antwort ist einfach - das Vorhandensein des ganzzahligen Teils als Ergebnis. Wir haben uns jedoch über den Zeitraum und den Teil gewundert, der vor dem Zeitraum liegt (als Vorperiode bezeichnet), der jedoch nicht im gesamten Teil des Ergebnisses enthalten ist. Daher müssen wir nicht den gesamten Teil berücksichtigen. Daher können in diesem Beispiel alle Zahlen größer als 3 oder gleich von der Betrachtung ausgeschlossen werden. Und was noch interessanter ist - die Gesetze der Teilung manifestieren sich in vielerlei Hinsicht ohne eine andere Zahl als eine. Das heißt, es reicht aus, die Aufteilung einer Einheit in eine Reihe von ganzen Zahlen, großen Einheiten, zu untersuchen, und wir werden verstehen, wie alle gestellten Fragen zu beantworten sind, und gleichzeitig werden wir eine sehr anständige Anzahl neuer Sterne treffen.
In der Zwischenzeit haben wir nicht ernsthaft mit dem Thema begonnen - ein paar Tricks. Wissen Sie, dass das Teilen „umgekehrt“ erfolgen kann? Nicht wie wir es von der Schule gewohnt sind, aber vom Ende an. Lassen Sie uns dies in einem anderen Beispiel zeigen, in dem wir den letzten Rest nehmen und ausgehend davon die Bruchperiode berechnen. Denken Sie daran, dass der Rest beim Teilen von 5 durch 3 gleich 2 war. Was war die letzte Zahl, die wir abgezogen haben, um eine Zwei zu erhalten? Wir müssen uns nicht erinnern, weil wir wissen, dass wir immer die Zahlen vom vorherigen Rest multiplizieren, multipliziert mit 10, dh die letzte Ziffer des Dekrements ist immer gleich 0. Dies bedeutet, dass es ausreicht, die Produkte des Tripels nach Zahlen von 1 bis 9 zu sortieren, = (3,6 , 9,12,15,18,21,24,27), um zu sehen - unter ihnen endet nur eine mit 8 und ergibt insgesamt mit dem Rest 2 Null in der letzten Ziffer der dekrementierten Eins. Bevor wir also den Rest von 2 erhalten, haben wir 18 von 20 subtrahiert. Warum von 20? Weil jede andere Zahl mit Null in der letzten Ziffer die Differenz X0-18 mehr als drei oder weniger als Null ergibt. Auf die gleiche Weise berechnen wir alle anderen Zahlen:
2 - bekannter Rückstand
18 - Addition zur Zahl mit Null, wobei gleichzeitig der Wert der nächsten Ziffer als Ergebnis angezeigt wird - 6 (6 * 3 = 18)
20 ist eine geeignete Zahl mit Null
2 - eine Zahl mit Null vor dem Multiplizieren mit 10 (= 20/10)
18 - Addition zur Zahl mit Null
20 ist eine geeignete Zahl mit Null
...
Als Ergebnis erhalten wir genau die gleiche Reihenfolge wie beim Teilen durch eine Ecke, jedoch "auf der anderen Seite". So können Sie „ab dem Ende“ die Periode aller periodischen Brüche berechnen. Und was ist die Vorperiode (und die Irrelevanz ihrer Berechnung für diesen Fall in der gezeigten Weise), werden wir weiter sehen. Der gesamte Teil des Ergebnisses ist immer Null, wenn die Einheit als Dividende verwendet wird. Daher müssen wir außer dem Zeitraum erneut nichts anderes berechnen.
Denken Sie nun daran, wie wir die Einheit in drei Teile teilen:
1 / 3 = 0 , 3 ( 3 ) . Hier ist alles einfach, die Periode ist kurz, es gibt keine Vorperiode, es scheint nichts Bemerkenswertes zu sein. Aber versuchen wir noch einmal, das Ergebnis der Division mit drei zu multiplizieren:
0 , 3 ( 3 ) ≤ 3 = 0 , 9 ( 9 ) , also
0 , 9 ( 9 ) / 3 = 0 , 3 ( 3 ) . Und am Anfang war es so:
1 / 3 = 0 , 3 ( 3 ) . Den Unterschied nicht bemerken? Es gab eine am Eingang, und nach direkten und umgekehrten Aktionen erhalten wir ... Wie könnte ich es einfacher nennen? Das heißt, wenn wir die gesamte Neunerkette bis ins Unendliche verfolgen, werden wir verstehen, dass wir eine Einheit haben, aber es ist irgendwie nicht so, können Sie es finden? Nun, nicht wie das Original, und das war's. Mathematiker werden sagen, dass dies nur zwei Formen der Notation derselben Zahl sind, aber das alltägliche Verständnis der „gleichen“ Rebellen rebelliert ein wenig gegen solche Definitionen. Im Prinzip ist es schwierig, mit Mathematikern nicht einverstanden zu sein, da sich viele Neunen nach dem Dezimalpunkt von der Einheit durch etwas völlig Vergängliches, unendlich Kleines unterscheiden und im Grenzbereich gegen Null tendieren. Aber können Sie diese ganze Menge von Unendlichkeiten mit Ihrem Verstand erfassen? Eine unendliche Anzahl von Neunen, ein unendlich kleiner Unterschied, der gegen Null tendiert, wenn man sich entlang einer Reihe von Neunen bis ins Unendliche bewegt. Und jetzt vergleichen Sie dies mit einer solchen Aufzeichnung - 1. Ein Zeichen - und alles ist uns klar. Und wie viele Anzeichen gab es in Diskussionen über die Gleichheit einer unendlichen Anzahl von Neunen mit einem? Das heißt, es gibt immer noch einen Unterschied? Oder ignoriert Ihr Gehirn solche Kleinigkeiten in einer Reihe von Unterschieden leicht? Aber wenn wir nicht zu dem endlosen mentalen Blick in der Liste der Neunen gehen, dann wird es an der Stelle, an der wir aufhören, sofort einen Unterschied geben, den selbst Mathematiker als signifikant erkennen - wenn Sie nicht alle anderen Neunen sehen, dann sind wir überhaupt keine. Daher stellt sich die Frage: Kannst du bis in die Tiefen aller Unendlichkeit sehen? Im Allgemeinen haben Mathematiker, was auch immer Sie wollen, angeordnet, dass dieses Phänomen als dieselbe Zahl betrachtet wird. Nachdem wir diesen Stern betrachtet haben (mit der Offenheit - ein seltsames Leuchten), fahren wir mit dem nächsten fort.
Eine interessante Schlussfolgerung ergibt sich aus der Tatsache, dass eine unendliche Anzahl von Neunen entdeckt wird - wenn der Teiler der Einheit eine Primzahl größer als 3 ist, wird die resultierende Periode immer durch 9 und natürlich durch 3 geteilt und auch mit ihrer Länge mehr als ein Zeichen - durch 11 und wann noch mehr Zeichen - 13, 37, 101 und so weiter. Und das alles unabhängig vom Einheitenteiler, wenn es nur einfach wäre und mehr als drei. Sie können dies selbst überprüfen, indem Sie beispielsweise die 1/7 Periode gleich 142857 durch 3, 9, 11, 13, 37 teilen.
Nun, vor den Haufen stellen wir eine einfache Frage: Ist es möglich, die Periode selbst zu konstruieren? Ja, das kannst du. Zum Beispiel möchten wir den Zeitraum 0123456789 erhalten. Können wir eine Dividende und einen Divisor finden, die etwas Ähnliches geben? Sie können! Aber ohne die Nummer 8. Dann wird es 1/81 sein. Und damit die Zahl 8 an ihrer richtigen Stelle erscheint, müssen wir der Zahl 81 einige Stellen nach dem Dezimalpunkt oder ohne Dezimalpunkt hinzufügen, aber dann sind in der Periode viele Nullen vorhanden.
Eine weitere Regelmäßigkeit: Bei einigen Einheitenteilern können wir die Periode überhaupt nicht berechnen, sondern sie einfach zyklisch verschieben, wenn wir die Dividende (Einheit) mit einer beliebigen Zahl multiplizieren. Zum Beispiel - 1/7 = 0. (142857) und 2/7 = 0. (285714), 5/7 = 0. (714285), 3/7 = 0. (428571) und so weiter. Wenn die Dividende größer als 7 ist, wird der gesamte Teil des Divisionsergebnisses auf den Teil vor dem Dezimalpunkt verschoben, und die Periode besteht weiterhin aus denselben sechs Ziffern, wird jedoch erneut zyklisch verschoben - 25/7 = 3. (571428), 86/7 = 12. (285714) usw. Wie gefällt dir das? Jede durch 7 geteilte Zahl ergibt die gleichen Zahlen! Jeder! Absolut keine. Und ja, diese "beliebigen Zahlen" sind eine unendliche Zahl. Und das Ergebnis enthält immer 6 gleiche Zahlen. Außerdem werden Sie verstehen, warum die Welt der Zahlen so strukturiert ist. Im Moment stellen wir jedoch fest, dass wir beim Teilen der Einheit durch 7 implizit alle erforderlichen Informationen erhalten haben, um den Zeitraum aus dem Ergebnis aller anderen Zahlen mit sieben zu berechnen, da wir jetzt wissen, dass es ausreicht, nur eine zyklisch zu verschieben das einzige Ergebnis der Teilung. Das heißt, es wird erneut bestätigt, dass es nicht erforderlich ist, die Division von Zahlen außer einer durch die für die Studie ausgewählte Zahl zu behandeln. Es kann zwar notwendig sein, mit einigen Zahlen zu multiplizieren und sich Zwischenergebnisse zu merken, aber dazu später mehr.
Für eine allgemeinere Ansicht zeigen wir nun die „Schlachtkarte“. Es wird eine Karte gezeichnet, um die Einheit durch die untersuchte Zahl zu teilen, während die Teilung in allen Zahlensystemen mit einer Basis durchgeführt wird, die kleiner als die untersuchte Zahl ist. Die Karte enthält nicht das Ergebnis der Division, dh den Zeitraum des betreffenden Bruchs, sondern die Residuen, die in jeder Stufe der Division durch die „Ecke“ erhalten wurden. So sieht es aus:
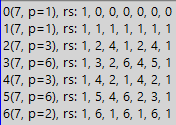
In der obigen Tabelle sehen Sie die Zeilen von 0 bis 6. 0 ist auch die Basis für das Zahlensystem. Stimmen Sie nicht zu? Versuchen wir zu überzeugen. Was ist ein Zahlensystem? Dies ist die Basis, die mit einem bestimmten Wert multipliziert und dann zum Ergebnis addiert wird, das ganz am Anfang Null ist. So werden beispielsweise alle Zahlen im Dezimalzahlensystem erhalten. Und wenn die Basis Null ist? Dann sind auch alle mit Null multiplizierten Terme gleich Null. Aber was ändert sich daran? Haben wir gegen die Regel verstoßen, Zahlen im gewählten Zahlensystem zu konstruieren? Daher verwenden wir für die Allgemeinheit des Bildes auf der Schlachtkarte alle Zahlensysteme von 0 bis 6, wenn wir die Zahl 7 studieren. Zusätzlich zur Allgemeinheit hat die Linie mit Nullen jedoch einen zusätzlichen Zweck.
Aber was bedeuten all diese Zeilen? Jede Zeile zeigt uns die Reihenfolge der Reste, wenn die Einheit im Zahlensystem, das in der linken Spalte signiert ist, durch sieben geteilt wird. Das heißt, wenn wir 1/7 in einem System mit einer Basis von 0 teilen, haben wir einen anfänglichen Rest von 1 (die Einheit, die wir teilen). Wie immer beim Teilen durch eine Ecke multiplizieren wir den ersten Rest mit der Basis des Zahlensystems. Wir bekommen Null. Jetzt ist Null der aktuelle Rest. Wenn Sie den Quotienten nach Erhalt des Restbetrags gleich Null berechnen und die teilbare Zahl keine zusätzlichen Ziffern enthält, wird die Division normalerweise gestoppt (da das Ergebnis erhalten wird). In unserem Fall füllen wir jedoch eine Tabelle aus, die keine Leere toleriert. Zusätzlich zur Ungeduld weist sie zusätzliche Eigenschaften auf, die auch das Vorhandensein beliebiger Zahlen in allen Zellen erfordern. Daher teilen und dividieren wir den Rest von 0 weiter durch 7. Während der Rest kleiner als der Divisor ist, wird er normalerweise mit der Basis des Zahlensystems multipliziert, aber das mehrfache Multiplizieren mit Null ist nutzlos. Wir schreiben also einfach, dass der Rest nach dem Multiplizieren mit Null wieder Null wird und Legen Sie es nun in die Tabelle in der nächsten Zelle. Wiederholen Sie dann den Vorgang. Und so füllen wir alle Zellen in der ersten Zeile mit Nullen. Und dann füllen Sie die zweite Zeile aus. Aber es hat bereits eine andere Basis des Zahlensystems - eine Einheit. Nachdem wir 1 durch 7 geteilt haben, haben wir den ersten Rest - einen. Dann multiplizieren wir mit der Basis des Zahlensystems, dh mit eins. Wir bekommen wieder 1. Wir schreiben in die entsprechende Zelle. Wieder multiplizieren wir mit 1, wieder bekommen wir 1, wir schreiben wieder. Und so weiter, bis die zweite Zeile gefüllt ist. Aber nach diesen beiden wunderbaren Zeilen in jeder Hinsicht kommen wir endlich zu einer aussagekräftigeren Trennung - im binären System (und die Bedeutung der ersten beiden Systeme wird später klar). Zuerst haben wir die gleiche Einheit. Schreiben Sie die Einheit in die dritte Zeile. Dann multiplizieren wir mit der Basis des Zahlensystems (mit 2). Wir erhalten 2. 2 weniger als sieben, wir können noch nicht subtrahieren, also schreiben wir den Rest 2 in die Tabelle. Wieder multiplizieren wir mit 2, wir erhalten 4, was wiederum weniger als 7 ist, also geht es wieder ohne Änderungen zur Tabelle. Aber im nächsten Schritt erhalten wir 8, was mehr als 7 ist, also müssen wir subtrahieren. Das Ergebnis ist 1. Wir schreiben in die Tabelle. Aber früher hatten wir bereits eine Einheit, so dass alle anderen Schritte gleich sind - also werden wir die dritte Zeile am Ende hinzufügen. Und auf die gleiche Weise werden wir den Rest der Zeilen hinzufügen, aber nicht vergessen, dass wir mit einer anderen Basis des Zahlensystems multiplizieren müssen.
Wenn wir also endlich die fertige Tabelle haben, können wir einige Schlussfolgerungen ziehen. Achten Sie zunächst auf Wiederholungen. Für das binäre System haben wir 1,2,4,1,2,4,1, dh zweimal 1,2,4 und dann noch einmal 1. Hier entspricht die Liste 1,2,4 der Periode des resultierenden binären Bruchs. Das heißt, der Zeitraum wird Länge 3 sein. Und obwohl wir die Reste anstelle der Zahlen aus dem Zeitraum verwendet haben, hat die Länge nicht darunter gelitten, und daher werden alle Informationen gespeichert. Und noch mehr - in der Tabelle gibt es wirklich mehr Informationsreste. Aber dazu später mehr, aber im Moment stellen wir fest, dass alle Linien zur Erleichterung des Studiums und aufgrund des Vorhandenseins einer solchen Anzahl nützlicher Eigenschaften gleich lang sind. Die Linien beginnen und enden also mit Einheiten, was die Eigenschaften der Zahl 7 gut unterscheidet. Und wenn wir die Linien auf die Länge der Periode reduzieren würden, könnten wir die Schönheit der symmetrischen Darstellung der Essenz der Zahl 7 nicht genießen.
Nun zu den Informationen. Die Salden setzen die Zahl eindeutig an der entsprechenden Position der Periode, daher gehen die Informationen in dieser Darstellung nicht verloren, aber da die Salden größer sein können, beispielsweise das Maximum einer Dezimalstelle (d. H. 9), werden die Informationen mit ihrer Teilnahme die vollständigste, weil eine Position im System Die Berechnung kann uns nicht sagen, dass der Rest beispielsweise 19 war, aber der Rest 19 zeigt deutlich, welche Zahl in der Periode liegt und von welchem vorherigen Rest wir das Produkt der Dividende abgezogen haben (denken Sie an den Fokus mit Division „vom Ende“). Und außerdem fällt uns sofort eine einfache Sache auf: Es kann nicht mehr Rückstände geben als
N - 1 wo
N. - die untersuchte Zahl, durch die wir die Einheit teilen. Dies ist ein sehr wichtiger Punkt. Darüber hinaus kann leicht nachgewiesen werden, dass, wenn ein zuvor angetroffener Rest beim Teilen durch eine Ecke wiederholt wird, die gesamte Sequenz von Resten, die dem zuvor wiederholten Wert folgten, wiederholt wird. Wir müssen es also nicht mehr nehmen, sobald die Periode gefunden ist. Wenn wir nur die Zahlen aus der Periode aufzeichnen, bedeutet das Wiederholen der Zahlen in der Periode nicht den Abschluss der Berechnung. Salden sind daher wichtiger als Zahlen aus der Zeit. Aber das Interessanteste sind die Überreste von allem
N - 1 und daher sind die Perioden länger
N - 1 kann nicht sein. Hier haben wir also gerade die Obergrenze der Anzahl der Stellen in der Periode gefunden, die von den tatsächlichen Stellen der Periode zu den Salden übergeht. Wie sie sagen, leichte Handbewegung und kein Betrug. Dies ist der Vorteil vollständigerer Informationen. Nun, daher beträgt die Breite unserer „Kampfkarte“ für 7 Übereinstimmungen 6 + 1 Spalten, dh 6 Spalten für alle möglichen Reste und 1 Spalte für die Erkennung der Symmetrie von Einheiten, was keineswegs für alle Zahlen obligatorisch ist und daher nicht Es lohnt sich, sich zu verstecken und Platz unter einer Spalte zu sparen.
Schauen Sie sich nun die obige „Karte“ hinsichtlich ihrer Nützlichkeit an. Sie können sofort eine Reihe einfacher Muster bemerken. Jede Zeile beginnt mit einer Einheit und endet damit. Die zweite Position jeder Zeile gibt die Basis des Zahlensystems an, aber die Mitte jeder Zeile enthält entweder N-1 oder 1. Beachten Sie, dass wir keine Anstrengungen unternommen haben, um die Zahlen in der Tabelle in dieser Reihenfolge anzuordnen, außer einfach die Teilungsergebnisse in der Tabelle festzulegen. Aber obwohl wir jede Reihenfolge ignoriert haben (mit Ausnahme der Reihenfolge der Teilungsschritte), entstand die Reihenfolge selbst aus dem Nichts und zeichnete uns den Buchstaben P aus Einheiten, setzte eine Kappe aus Nullen (mit einem Visier von eins) darauf, teilte die Tabelle durch eine mittlere Spalte von Einheiten und seine Ergänzungen zur Zahl 7 (gemäß der Formel 7-1 = 6). Darüber hinaus platzierte die Bestellung selbst die Zahlensysteme in der zweiten Spalte. Vergleichen Sie es mit den Zahlen in der ersten linken Spalte, sie werden nur absichtlich hinzugefügt, damit wir genau wissen, wo sich das Zahlensystem befindet. Nun, wir können die Periode der resultierenden Brüche leicht selbst berechnen, obwohl sie der Einfachheit halber in der Spalte mit Werten der Form p = X angegeben ist.
In der Tat, bevor Sie so etwas wie ein Periodensystem ist, aber nicht für die Chemie, sondern für die Zahlentheorie. Genau wie bei Mendeleev können Sie in der Tabelle ein bestimmtes Muster finden und dann, genau wie nach Mendeleev, die Existenz dieses Musters begründen und beweisen, dass es für alle Zahlen wiederholt wird, die bestimmte Bedingungen erfüllen. Und das ist das Wichtigste in solchen Tabellen. Wenn Sie nur Muster betrachten und beobachten, können Sie Gesetze entdecken, zum Beispiel die Zahlentheorie. Nun, für nachdenklichere Leser öffnet sich hier der Weg zu einem vollständigen Zyklus - nachdem Sie ein Muster gefunden haben, müssen Sie seine Relevanz für alle Zahlen oder für Zahlen einer bestimmten Klasse beweisen (oder widerlegen).
Wie bereits erwähnt, enthält diese Tabelle vollständige Informationen zur Primzahl 7. Aus diesen Informationen können wir jedoch Hypothesen zu allen Primzahlen ableiten. Und selbst einige dieser Hypothesen wurden uns bereits bewiesen, sodass wir nur die Schlussfolgerungen anderer überprüfen müssen. Beweise wurden von so berühmten Personen wie zum Beispiel Fermat und Euler gegeben. Farm gab uns diese Formel
a ( p - 1 ) p m o d p = 1 (hier nimmt die Mod-Operation den Rest der Division des Wertes links durch den Wert rechts, bei der Programmierung wird dies normalerweise durch das% -Symbol angezeigt), dh den Rest der Division
a ( p - 1 ) on p ist für alle Primzahlen immer gleich eins (nämlich Primzahlen, das ist wichtig). Aber die Zahl 7 ist auch Primzahl. Und jeder Rest in jeder Zeile kann mit der folgenden Formel berechnet werden:
bi pmodN=r . Hier ist b die Basis des Zahlensystems (aus der englischen Basis), i ist die Positionsnummer in der Zeile (aus dem englischen Index), beginnend mit Null für die erste Position, N ist die zu untersuchende Nummer (in diesem Fall - 7), r ist der Rest (aus der englischen Erinnerung) ) gebildet im i-ten Schritt des Teilens durch eine Ecke und enthalten in der i-ten Spalte der Tabelle. Vergleichen wir die Fermat-Formel und die Formel zur Berechnung des durch Index i angegebenen Restes. Sie sind für das letzte Mitglied aller Sequenzen von Resten identisch. Und in voller Übereinstimmung mit der Fermat-Formel für jeden Rest in Position
N−1 Wir haben Gleichheit mit der Einheit. Das heißt, das mit bloßem Auge beobachtete Muster in Form einer Einheitensäule wurde in den Tagen von Fermat bestätigt und bewiesen (obwohl Fermat uns keine Beweise gab, aber normalerweise waren alle seine Aussagen wahr). Euler fügte der Formel von Fermat die Möglichkeit hinzu, sie nicht nur für Primzahlen, sondern auch für zusammengesetzte Zahlen zu verwenden. Sie müssen zwar alle Teiler einer Zahl kennen, aber für kleine Zahlen ist dies kein Problem. In der zweiten Tabelle (unten) sehen wir also die Sequenz der Reste für die Nummer 21, die zusammengesetzt ist. Euler hat bewiesen, dass der Rest der Division einer beliebigen Zahl in dem Maße, der der Anzahl kleinerer Zahlen entspricht und keine gemeinsamen Teiler mit N aufweist, ebenfalls gleich eins ist. Und genau diese Tatsache beobachten wir in der Tabelle für die Zahl 21, für die von den 20 niedrigeren Zahlen 8 einen gemeinsamen Teiler mit 21 haben und 12 nicht. Daher beobachten wir in der 12. Spalte (wenn von Grund auf neu indiziert) viele Einheiten. Und diese Einheiten stehen nicht am Ende der Zeilen, da einige der Zahlen, die kleiner als 21 sind, gemeinsame Teiler mit 21 haben.
Bei Primzahlen hat jedoch keine kleinere Zahl gemeinsame Teiler, so dass die Anzahl der Zahlen ohne gemeinsame Teiler in einfachen Fällen immer größer ist als in zusammengesetzten Zahlen. Und deshalb sind die Einheitsreste in der Tabelle für einfache weiter entfernt als für zusammengesetzte. Beachten Sie jedoch, dass nicht alle Werte in der 12. Spalte der Tabelle für 21 gleich eins sind. Ist Euler falsch? Nein, er hatte einfach nicht vor, seine Formel für die Arbeit mit Zahlen zu verwenden, die reduziert werden können, und nur in den Zeilen, die Vielfache von 3 und 7 sind (Teiler von 21), haben wir eine Diskrepanz mit der Euler-Formel. Im Allgemeinen stellt sich heraus, dass Fermat und Euler uns geeignete Formeln gegeben haben, die zum Verständnis der Probleme der Teilbarkeit von Zahlen nützlich sind, und die obigen Tabellen in all ihrer Pracht bestätigen die Ergebnisse von Euler und Fermat.
Von Sternen zu Magie
Puzzle-Liebhaber kennen die sogenannten "magischen Quadrate". Dies sind Tabellen, in denen Sie die Zahlen so anordnen müssen, dass die Summen entlang der Vertikalen, Horizontalen und zwei Diagonalen gleich sind. Viele Leute rätselten lange Zeit immer wieder und legten Zahlen in das Prokrustes-Bett, um die Beträge einzuschränken, und schafften es sogar, ziemlich große Quadrate auszufüllen. Aber heute haben wir viel mächtigere Magie erlebt. Ja, das Periodensystem für die Zahlentheorie enthält viel mehr Einschränkungen, und selbst ein Erstklässler, der lernen kann, die „Ecke“ zu teilen, kann sie füllen. Denken Sie darüber nach - die klügsten Leute füllten die magischen Quadrate, aber sie fanden keine übliche Methode zum Füllen oder erreichten sogar eine Größe von elenden hundert Spalten. Und der Erstklässler wird sogar eine Milliarde vollständig bewältigen können, wenn er nur genug Zeit zur Verfügung hätte.Hier ist eine solche Galaxie, die mit Sternen bis zu den Augäpfeln gefüllt ist und in numerischen Quadraten auf uns wartet.Beginnen wir mit der Auflistung der offensichtlichen Muster
Multiplikation Jede Zeile der Tabelle kann mit jeder anderen multipliziert werden. Das Ergebnis ist eine Reihe, deren Zahl als Produkt der Zahlen der multiplizierten Reihe geteilt durch den Rest durch die untersuchte Zahl berechnet wird. Das heißt, wenn wir Zeile 2 aus der Tabelle für 7 mit Zeile 3 multiplizieren, erhalten wir Zeile 6. Und wenn wir Zeile Zeile 4 mit Zeile 6 multiplizieren, erhalten wir 24 mod 7 = 3, dh die dritte Zeile. Und die Eigenschaft der Division modulo (dh mit dem Rest) macht alle Zahlensysteme, die größer als die untersuchte Zahl sind, unnötig. Wir brauchen also kein Zahlensystem mit Basis 24, da die Werte der Residuen darin genau die gleichen sind wie im System mit Basis 3. In jedem Zahlensystem, in dem wir die Reste aus der 1/7 Division berechnen, erhalten wir immer ein Ergebnis, das bereits vorliegt ist in der Tabelle. Interessant? Und das ist nur der Anfang.Symmetrie Jede zweite Spalte enthält den oberen und unteren Teil, die sich gegenseitig widerspiegeln. Die verbleibenden Spalten enthalten Werte, die dem Komplement des N-reflektierten Gleichgewichts entsprechen. Das heißt, in der zweiten Spalte der Tabelle für die Nummer 7 ergänzt die Nummer 1 die Ergänzungen 6 bis 7, 2 die Ergänzungen 5 und 3 die Ergänzungen 4. Als Ergebnis wird die oben betrachtete Formel verwendetb i( modN ) = r wird durch folgendes System ergänzt:( N - j ) i( modN ) = r für ungerade Spaltenj i( modN ) = r für gerade Spaltenj = N - b Hier ist N die untersuchte Zahl (zum Beispiel 7), b ist die Basis des Zahlensystems, i ist der Spaltenindex ab Null, r ist der Restwert in der gegebenen b- und i-Zelle.Die horizontale Symmetrie wird durch die zuvor erwähnten extremen Spalten von Einheiten und die mittlere Spalte von Einheiten und deren Ergänzung zu N ausgedrückt. Dies funktioniert genau für Primzahlen, aber für Bestandteile gibt es Abweichungen. Zusätzlich (wieder nur für Primzahlen, manchmal aber auch für Bestandteile) beginnt die teilende mittlere Spalte immer entweder mit einer Einheit der Wiederholungsperiode der Residuen oder gibt rechts eine Reihe von Additionen zu N für die linke Hälfte der Reihe an. Wenn sich die Einheit in der mittleren Spalte befindet, wird der linke Teil wiederholt. Wenn es eine Addition zu N gibt, geht dieselbe linke Seite weiter, aber nach dem Subtrahieren von N. Somit können Sie von der gesamten Tabelle (für Primzahlen) nur das obere linke Quadrat mit der Seite belassen( N - 1 ) / 2 (ohne Nullzeile) und alle anderen Restwerte werden eindeutig basierend auf Informationen aus einem solchen Quadrat abgeleitet. Obwohl Sie nicht vergessen sollten, dass im Allgemeinen die gesamte Tabelle aus der Kenntnis einer einzelnen Zahl - des Divisors - abgeleitet wird, während die Dividende eine Konstante gleich 1 ist.Nun die Summe. Grundsätzlich werden für einfache, manchmal aber auch für zusammengesetzte Regeln die folgenden Regeln befolgt. Die horizontale Summe (ohne die letzte Spalte, die der Übersichtlichkeit halber hinzugefügt wurde) ist immer ein Vielfaches der untersuchten Zahl. Die vertikale Summe ist auch immer ein Vielfaches der untersuchten Zahl. Die Summen der Salden innerhalb des Zeitraums von eins bis eins (der Zeitraum kann kleiner als die Breite der Tabelle sein) sind entweder mehrfach oder gleich der untersuchten Zahl.Weitere Teilbarkeit. Zeilen von Residuen zwischen Einheiten (Perioden von Residuen) können unterschiedlich lang sein, aber alle Zeilenlängen für Primzahlen teilen die Gesamtlänge der Tabelle immer durch eine Ganzzahl. Das heißt, wenn mindestens eine Zeile zwischen Einheiten die Gesamtlänge der Tabelle nicht vollständig aufteilt, handelt es sich um eine zusammengesetzte Zahl (vergleichen Sie die Tabellen für 21 und 7).Länge und Einzigartigkeit. Jede Reihe mit gerader Länge und kürzer als die Breite der Tabelle besteht aus zwei Teilen - einer Reihe von Resten in der Mitte und danach einer Reihe von Ergänzungen zu N für die anfängliche Reihe von Resten. Darüber hinaus sind alle Werte innerhalb der Periode eindeutig, dh sie werden nur mit der Wiederholung der Periode wiederholt, aber innerhalb der Periode werden sie niemals wiederholt.Multiplikation. Wenn jede Zelle der Tabelle mit einer ganzen Zahl multipliziert wird, erhalten wir entweder eine zyklische Verschiebung der Reste bei einer Periodenlänge, die der Breite der Tabelle entspricht, oder eine neue Reihe bei Fällen, bei denen die Periode kürzer als die Breite der Tabelle ist. Darüber hinaus sind bei kurzen Zeiträumen alle Werte in der neuen Reihe eindeutig, dh keiner von ihnen ist in der Reihe enthalten, die durch Teilen der Einheit durch die untersuchte Zahl erhalten wurde, sowie in der Reihe, die durch Multiplizieren mit anderen Zahlen erhalten wurde, und in der ursprünglichen Reihe, die wir erhalten haben multipliziert mit einer Konstanten. Insgesamt entspricht die Anzahl der eindeutigen Perioden der Breite der Tabelle geteilt durch die Länge der Periode (für Primzahlen). Und für Komponenten in allen möglichen Zeiträumen gibt es keine „verbotenen“ Reste, die, multipliziert mit Zeilen, die durch die Teiler der untersuchten Zahl teilbar sind, einen Rest von Null ergeben, aber dazu später mehr.Infolge der Reihenmultiplikation kann man entweder eine zyklische Periodenverschiebung oder eine neue Periode erhalten. Die neue Periode kann auch zyklisch verschoben und mit anderen Werten multipliziert werden. Die allgemeine Regel für die Auswahl einer Schicht oder einer neuen Periode ist einfach: Wenn es in der verbleibenden Periode eine Zahl gibt, mit der wir multiplizieren, erhalten wir eine zyklische Verschiebung, und wenn es keine solche Zahl gibt, erhalten wir eine neue Reihe. Und dies gilt natürlich direkt für periodische Brüche, genauer gesagt für ihre Perioden (es ist notwendig, Perioden von Salden von Perioden von Zahlen im Bruchdatensatz zu unterscheiden, obwohl der Unterschied normalerweise aus dem Kontext hervorgeht). Im zuvor gezeigten Beispiel der Zahl 7 haben wir gesehen, dass unabhängig davon, wie Sie das Ergebnis der Division mit 7 multiplizieren, wir immer den gleichen Satz von Ziffern in der Periode erhalten, jedoch zyklisch relativ zur Standarddivision 1/7 verschoben sind. Bei der Zahl 7 haben wir einen Punkt (in Dezimalschreibweise) mit einer Länge,In Übereinstimmung mit der Breite der Tabelle können daher keine anderen Zahlen darin erhalten werden (es sind keine Salden mehr verfügbar), sondern es sind nur zyklische Verschiebungen möglich. Aber es gibt noch einen Punkt - wir haben im Dezimalsystem geteilt, aber es gibt keine solche Zeile in der Tabelle. Dies bedeutet, dass wir, um es zu finden, 10 durch 7 teilen und den Rest - 3 erhalten müssen. Es ist das Zahlensystem mit Basis 3, das das Verhalten des Dezimalsystems in Bezug auf die Reste vollständig wiederholt. Daher sehen wir in der dritten Zeile die gesamte Periode, dh mit einer Länge gleich die Breite der Tabelle. Und um die Periode in Dezimalzahlen aus den Salden zu erhalten, können Sie einen beliebigen Rest nehmen und ihn durch die Ecke dividieren. Infolgedessen werden alle Ziffern der Bruchperiode angezeigt. Die Verschiebung der Periode während der Multiplikation wird bestimmt, indem der Rest der Division des Faktors durch N in der Reihe der Residuen ermittelt wird. Die Verschiebung entspricht dem Index des gefundenen Guthabens.Das heißt, wir müssen die Periode immer zyklisch von rechts nach links um die Anzahl der Stellen verschieben, die dem Index des gefundenen Rests entspricht.Und ein paar Abhängigkeiten zwischen den verschiedenen untersuchten Zahlen:Hier sehen wir Zeilen für Zahlen von 2 bis 39 im Binärsystem. Achten Sie auf die untere Reihe. Spalten mit den Nummern 1,2,4,8,16,32 gehen davon aus. Nach der Zahl 32 sehen wir eine Wertespalte, die um eins zunimmt (25,26,27, ...). In der nächsten Spalte erhöhen sich die Werte um drei. Dann am 6, 13, 26 usw. Die Erhöhung „wechselt“ nach Erreichen eines Werts, der größer als die zu untersuchende Zahl ist (die Spalte links in Klammern vor der Länge des Zeitraums). Das Wachstum um eins wechselt also zu Wachstum um zwei, dann um drei usw. Im Allgemeinen beginnen alle diese Spalten mit2 i , wobei i der Spaltenindex ist. Unten
2 i der Wert ändert sich nicht, aber darüber ändert er sich gemäß der Formel2 i / j , wobei j das Inkrement beim Verschieben einer Zeile nach oben ist (größer als Null). Das heißt, während die Zeilennummer zwischen liegt2 i / j und
2 i / ( j + 1 ) ist das Inkrement gleich j. Nach dem Überqueren der Grenze2 i / ( j + 1 ) wird das Inkrement gleichj + 1 , dann ist die Grenze2 i / ( j + 2 ) , danach wird das Inkrement seinj + 2 usw.
Genau die gleiche Regelmäßigkeit ist für jede Basis von Zahlensystemen charakteristisch, dh alle Zeilen können durch Zeilen des Zahlensystems 10 (und im Bild sehen wir die Ergebnisse für das Binärsystem) oder eine andere ersetzt werden, und gleichzeitig bleibt die Regelmäßigkeit erhalten, jedoch mit der Ersetzung 2 in der Formel auf einer anderen Basis des Zahlensystems.Das Obige ist keine vollständige Liste von Mustern, aber Rätselliebhaber haben wahrscheinlich bereits genug, um zu versuchen, ein ähnliches Quadrat auszufüllen, beispielsweise für die Primzahlen 11, 13, 17. Versuchen Sie es, aber verwenden Sie nicht die Methode der Division durch Ecke oder Potenzierung. Plötzlich werden Sie eine andere Regelmäßigkeit entdecken, durch die solche Quadrate gebildet werden!Vorhersagen
Besitzer von Kristallkugeln neigen dazu, die Zukunft vorherzusagen, aber wir können auch etwas aus unseren Tabellen vorhersagen. Sie haben es wahrscheinlich schon bemerkt - die letzten geraden Spalten von Einheiten werden nur in Primzahlen gefunden. Das heißt, ein Blick auf die Tabelle reicht aus, um zu verstehen, ob eine Zahl eine Primzahl ist oder nicht. Dies ist die erste Vorhersage für unsere Kristallkugel. Die zweite Vorhersage ist die Bruchperiode im Zahlensystemk ∗ N - 1 (hier ist k eine ganze Zahl größer als Null) ist immer 2. Die Bruchperiode im Zahlensystemk ∗ N + 1 ist immer gleich 1 und alle Werte darin sind auch gleich 1. Zum Beispiel haben wir für die untersuchte Zahl N = 11 mit k = 1k ∗ N - 1 = 10 , dh im Dezimalzahlensystem1 / 11 = 0 ( 09 ) , die Periodenlänge gleich 2, wieoben vorhergesagt. Nun sagen wir die Ergänzung zu den Formeln Euler und Fermat voraus. Denken Sie zunächst daran, dass jeder Rest berechnet werden kann, indem seine Positionsnummer und die Basis des Zahlensystems unter Verwendung der Formel verwendet werdenb i( modN ) , wobei b die Basis des Zahlensystems ist, i die Position beginnend bei Null ist, N die untersuchte Zahl ist. Diese Formel entspricht den Formeln von Fermat und Euler, wenn wir darin die Position einnehmen, die den von Fermat und Euler vorgeschlagenen Werten entspricht. Aber neben dem Mustera ( p - 1 )( modp ) = 1 von Fermat gegeben, die Regelmäßigkeit der mittleren Spalte gibt uns eine ähnliche Formel -a ( p - 1 ) / 2( modp ) = { 1 , p - 1 } , dh jede Zahl nach der Potenz einer Primzahl, minus eins geteilt durch 2, gibt uns entweder Einheit oder p-1, wobei p eine Primzahl ist. Die Formel kann auf den Fall erweitert werden, dass die Anzahl der Perioden von eins bis eins in der gesamten Tabelle ungerade und die Länge der Periode gerade ist. Dann
a k( modp ) = p - ( a ( p - 1 ) / 2 + k( modp ) ) , wobei k eine ganze Zahl ist, ist p eine Primzahl. Diese Formel spiegelt die Regelmäßigkeit der Wiederholung des zweiten Teils der Periode gleicher Länge wider, aber mit Subtraktion von der untersuchten Zahl wurde diese Abhängigkeit etwas höher beschrieben. Für eine gerade Anzahl von Perioden gleicher Länge kann man durch die Formel auch die Abhängigkeit der Reste aus der rechten Hälfte der Periode von den Resten aus der linken Hälfte ausdrücken. Jetzt werden wir vorhersagen, wie alle Teiler einer Zahl aus einer solchen Tabelle ermittelt werden können. Schauen Sie sich dazu noch einmal die Tabelle mit der Nummer 21 an:

