Nur Teilung oder wie man eine mathematische Theorie erstellt und 400.000 Dollar damit verdient. Serie Drei, Finale

In früheren Serien haben wir Bruchzahlen aus verschiedenen ungewöhnlichen Blickwinkeln betrachtet. In dieser Reihe werden wir nach der Einführung und einigen theoretischen Grundlagen versuchen, alles in einer bequemen Form zu sammeln und von den verfügbaren Informationen zu profitieren.

Suche nach einfach

Nachdem wir über die Eigenschaften der Residuentabelle gesprochen haben, können wir versuchen, das Wissen darüber auf das Verdienen anzuwenden. Daher finden es viele auf der Welt nützlich, nach großen Primzahlen zu suchen. Und selbst es gibt Organisationen, die bereit sind, jemandem viel Geld zu geben, der eine große Primzahl findet. Das Thema Quantencomputer ist aber auch weltweit beliebt. Warum? Weil es verspricht, ein bekanntes Kryptosystem zu hacken. Dies ist sozusagen der Werbeslogan des Quantencomputers, der es ermöglicht, jeden Entscheidungsträger davon zu überzeugen, Geld für eine so interessante Lektion bereitzustellen. Daher werden wir auch über dieses Thema sprechen.

Zuerst zeigen wir Ihnen, wie Sie nach Primzahlen suchen. Das Hauptproblem hierbei ist die Menge. Bei großen Zahlen gibt es einfach keine Algorithmen, mit denen Sie schnell überprüfen können, ob eine Primzahl vor uns liegt oder eine zusammengesetzte. Daher beträgt die maximale Ausfallzeit für heute weniger als 25 Millionen Dezimalstellen. Dies sind nur 10 Megabyte. Auf solchen Arrays zeigen moderne Prozessoren Millisekunden-Verarbeitungszeiten. Um jedoch zu überprüfen, ob eine Primzahl in unserem Array enthalten ist, verbraucht ein moderner Prozessor jahrzehntelang Strom und summt mit einem Lüfter. Das heißt, technisch gesehen ist die Größe des Prozessors nicht gut, aber die Anzahl der Operationen in bekannten Algorithmen für solch große Zahlen ist einfach riesig. Warum ist diese Situation?

Für Einfachheitstests wird beispielsweise die Aufzählung von Teilern verwendet. Aber wie viele Teiler müssen Sie für eine Zahl von zehn Megabyte durchlaufen? Die Antwort ist, dass selbst Atome mit Elektronen im gesamten Universum nur für einen winzigen Teil dieses Wertes ausreichen werden. Das heißt, wir brauchen eine große Anzahl von Universen, nur um all diese Teiler dort zu platzieren. Zu viel? Daher wird die Aufzählung von Teilern für Zehn-Megabyte-Zahlen in begrenztem Umfang angewendet (ja, das Universum lässt uns im Stich ...), aber zum Glück gibt es andere Algorithmen. Wir können Algorithmen unterscheiden, die keine Aufzählung von Teilern verwenden, und gleichzeitig wird garantiert, dass sie eine Antwort geben - einfach vor uns oder zusammengesetzt. Dies sind jedoch sehr langsame Algorithmen. Das heißt, sie sind natürlich in der Lage, Zahlen auf diese Weise hundert oder zweihundert Bit zu schleifen, aber zehn Megabyte sind für sie der Tod auf einmal. Deshalb muss man die kniffligen Wege gehen.

Das Problem bei allen Tricks ist jedoch, dass sie noch keine vollständige Teilbarkeitstheorie entwickelt haben. Wenn es vollständig wäre, würden wir schließlich sehr schnell die Antwort finden - eine Primzahl oder nicht. Genauer gesagt würde uns eine Theorie schnell einen Algorithmus zum Testen geben, der uns nicht bis zum thermischen Tod des Universums warten lässt. Deshalb geben sie denjenigen Boni, die so schnell wie möglich einen Algorithmus entwickeln, und vor allem eine ganze Theorie, um Algorithmen für alle Gelegenheiten bereitzustellen.

In der Zwischenzeit steht uns ein spezifischer Luc-Lemer-Test zur Verfügung, bei dem die Verbindung sehr spezifischer Mersenne-Zahlen mit einer bestimmten Reihenfolge verwendet wird, jedoch nicht der Rest der Teilung, wie wir kürzlich beobachtet haben, sondern die Summe der Grade einiger irrationaler Zahlen. Das heißt, der Einfachheitstest wurde von der Seite durchgeführt, sagen wir, nicht ganz offensichtlich, obwohl einige hier kompliziertere Vergleiche aufgreifen können. Aber warum waren die Grade irrationaler Zahlen den Einfachheitstests näher als alle anderen Errungenschaften der Zahlentheorie? Anscheinend, weil die Mathematik keine einfachen Lösungen kennt. Infolgedessen wurde eine Methode verwendet, die zwar nicht offensichtlich ist, aber immer noch funktioniert, und zwar aus dem Bereich, der den ganzzahligen Berechnungen nicht am nächsten kommt. In etwa hilft der Übergang von kartesischen zu Polarkoordinaten dabei, zusätzliche Methoden zu verwenden, die in kartesischen Koordinaten nur sehr schwer zu implementieren sind.

Neben dem Luc-Lemer-Test gibt es auch probabilistische Tests. Sie helfen dabei, garantierte zusammengesetzte Zahlen auszusortieren. Einer der aktiv verwendeten probabilistischen Tests ist also ein Test, der auf der Fermat-Formel basiert, über die wir kürzlich gesprochen haben. Wie arbeitet er? Sehr einfach - erinnern Sie sich an die Spalte mit den Einheiten rechts in der Resttabelle? Dies ist ein garantiertes Zeichen für die Einfachheit einer Zahl. Um die Überprüfung anhand der Fermat-Formel zu erklären, verwenden Mathematiker eine bestimmte Terminologie, die nur wenige Menschen verstehen. Wir gehen also nicht in diese mathematischen Dschungel, sondern erklären alles an den Fingern oder besser gesagt aus der Tabelle der Residuen. Um zu verstehen, wie der Rest in der letzten Spalte aussehen wird, müssen Sie entweder durch eine Spalte teilen und den Rest an der Position erreichen, die 1 enthält, oder diesen Rest mithilfe einer Formel berechnen, mit der Sie den Rest anhand der Positionsnummer und der Basis des Zahlensystems ermitteln können. Die erste Option für Zahlen mit einer Länge von zehn Megabyte benötigt fast unendlich viel Zeit, da die Breite der Tabelle N-1 beträgt, was bedeutet, dass die Tabelle für eine Zahl in der Größenordnung von einer Million mindestens eine Million Spalten enthält. Für eine Milliarde, eine Milliarde. Für eine Billion, eine Billion. Aber eine Billion, es sind nur 12 Dezimalstellen. Und wir interessieren uns für eine Zahl, in der weniger als 25 Millionen Zeichen vorkommen. Selbst eine Billion Reste durch die Methode der Teilung der Spalte müssen wir kaum weniger als eine halbe Stunde berechnen, und das sind nur 12 Dezimalstellen. Insgesamt! Im Vergleich zu 25 Millionen. Denken Sie, Sie haben genug Zeit, um auf diese Weise auf das Ergebnis zu warten? Deshalb ist es besser, den gewünschten Wert sofort mit der Formel zu berechnen. Und nur die Fermat-Formel entspricht der Formel zur Berechnung des Restes an der letzten Position in der Tabelle. Wenn der Zeitraum kürzer als die Breite der Tabelle ist, weiß die Mathematik noch nicht, wie sie berechnet werden soll, was bedeutet, dass wir in jedem Fall die letzte Spalte auswählen müssen. Die Mathematiker im Test prüfen einfach, ob der Rest in der letzten Spalte für das von ihnen gewählte Zahlensystem gleich eins ist (obwohl Mathematiker den Begriff des Zahlensystems nicht verwenden, gibt es für sie nur eine zu einer Potenz erhobene Basis). Wenn der Rest nicht gleich eins ist, ist die Anzahl garantiert zusammengesetzt. Wie wir im Beispiel der Tabelle für die Zahl 21 gesehen haben, ist es das Fehlen einer Einheit am Ende vieler Zeilen, die sie von den Tabellen für Primzahlen unterscheidet. Es gibt jedoch ein Problem. In einigen Zeilen gibt es möglicherweise noch Einheiten, die wir auch am Beispiel der Tabelle für 21 überprüfen können. Deshalb nennen Mathematiker den Test basierend auf der Formel von Fermat probabilistisch. Das heißt, sie wissen nicht, ob die Zahl eine Primzahl ist, wenn der Fermat-Test einen Rest von eins gefunden hat, da solche falschen Einheiten in der Tabelle für die Zahl 21 und in vielen anderen Tabellen sogar für Zehn-Megabyte-Zahlen enthalten sind. Sie müssen also entweder alle Zeilen in einer Zeile überprüfen, was sehr lange dauert, da die Zeilen für eine Zehn-Megabyte-Zahl, wie bereits erwähnt, viel mehr sind als alles in dem Universum, das wir kennen, oder einfach sagen - es ist wahrscheinlich, dass diese Zahl eine Primzahl ist. Hier ist die letzte Methode, die Mathematiker gewählt haben. Glücklicherweise gibt es in den meisten zusammengesetzten Zahlen nur wenige Zeilen, die mit einer enden. Es stimmt, es gibt auch die sogenannten Carmichael-Zahlen, in denen alle Zeilen außer Vielfachen der Teiler einer solchen Zahl mit eins enden. Bei Carmichael-Zahlen ist der Wahrscheinlichkeitstest nach der Fermat-Formel praktisch garantiert falsch, da zur Beseitigung des Fehlers ein Vielfaches des Zahlenteilers erforderlich ist und zehn Megabyte Teiler nur zwei haben können und ihr Wert sehr groß sein kann und daher die Wahrscheinlichkeit des Erhaltens es ist in einer solchen Linie, dass es bei einer zufälligen Wahl der Basis des Zahlensystems praktisch Null ist. Andererseits sind die Carmichael-Zahlen relativ klein, was uns erlaubt, auf einen Wahrscheinlichkeitstest zu hoffen. Nur bei der Suche nach Primzahlen wird die Hoffnung auf Wahrscheinlichkeit ausgeschlossen. Deshalb wird nach Auswahl von Kandidaten für einfache mit Hilfe von Wahrscheinlichkeitstests trotzdem der Luc-Lemer-Test angewendet.

Fügen Sie ein wenig über Carmichael-Zahlen hinzu. Sie zeichnen sich nicht nur durch ihre Fähigkeit aus, einfache nachzuahmen. Das Netzwerk verfügt also über eine Website, auf der Sie verschiedene Zahlenfolgen lernen können . Wenn Sie die Nummer 561 (die minimale Carmichael-Nummer) in das Suchfeld eingeben, können Sie feststellen, dass sie an einer sehr großen Anzahl von Sequenzen beteiligt ist. Worüber spricht das? Anscheinend über einige noch unbekannte strukturelle Eigenschaften ähnlicher Anzahl, die in unserer Welt sehr verbreitet sind. Sehr unterhaltsame Tatsache.

Aber zurück zu den Einfachheitstests. Trotz eines guten Filterkoeffizienten mit Wahrscheinlichkeitstests verbringt die Menschheit Jahre damit, die nächste maximale Primzahl zu finden. Warum? Weil die Abhängigkeit der Testausführungszeit von der Größe der Zahl quadratisch ist. Das heißt, bei kleinen Zahlen geht alles mit einem Knall los und es gibt keine Probleme, aber wenn sich die Zahlen millionenfach erhöhen, erhöht sich die Zeit für Berechnungen um eine Billion Mal. Daher würden wir auf einem einzelnen Prozessorkern den Luc-Lemer-Test für Jahrzehnte in Betracht ziehen. Aber auch einen Test nach der Fermat-Formel würden wir ungefähr gleich betrachten. Das heißt, in beiden Ansätzen hat die Anzahl der Berechnungen die Grenzen menschlicher Fähigkeiten erreicht. Du musst etwas damit anfangen, oder?

Was können die Alternativen zu solch einem verschwenderischen Rechenabfall bei der Luftheizung für viele Jahre sein? Sehr einfach - Sie müssen die Einfachheit anhand der Art der Zahl und ihrer Zugehörigkeit zu einer bestimmten Klasse vorhersagen. So wurden Mersenne-Zahlen gerade aufgrund ihrer Zugehörigkeit zu einer bestimmten Klasse führend in den erreichten Größen bewährter Primzahlen. Der Luke-Lemer-Test funktioniert speziell für eine bestimmte Klasse. Die Anzahl anderer Klassen bleibt zurück, da es nicht einmal einen so teuren Test wie den Luc-Lemer-Test für Zehn-Megabyte-Zahlen gibt (obwohl dieser Test für einige angepasst ist). Wir brauchen also eine Klassifizierung von Zahlen, die es uns ermöglicht, einfache Einfachheitstests zu finden. Der Himmel verzeiht mir ein solches Wortspiel.

Wie erstelle ich eine solche Klassifizierung? Es ist auch nicht so schwierig - Sie müssen verschiedene Zahlen studieren und gemeinsame Merkmale zwischen ihnen identifizieren. Im Allgemeinen ist dies genau das, was Mathematiker versuchen, aber bisher ist keine Steinblume herausgekommen. Deshalb werden wir versuchen, ihnen zu helfen.

Der zuvor beschriebene Ansatz zur Analyse von Zahlen auf der Grundlage von Residuentabellen untersucht im Wesentlichen die Teilbarkeit von Zahlen der Form 1000 ... 000. Das heißt, die Nullen auf der rechten Seite werden der Einheit ständig zugewiesen, wodurch sie mit der Basis jedes der in der Resttabelle vorhandenen Zahlensysteme multipliziert wird. Als Ergebnis der Analyse haben wir festgestellt, dass verschiedene Zahlen Zahlen der Form 1000 ... 000 auf unterschiedliche Weise teilen. Primzahlen können also im Allgemeinen keine Eins durch Nullen teilen. Aber die Komponenten und sogar zum Beispiel Zweien und / oder Fünfer sind vollständig geteilt. Unten ist die Tabelle für die Nummer 8:



Wie Sie darin sehen können, bleiben in Zeilen, die ein Vielfaches von 2 sind, nach einem Eintrag von Resten ungleich Null nur noch eine Null übrig. Genau so sehen alle Zahlen aus, die sich auf die Klasse der Teiler von Einheiten mit Nullen beziehen, und das Vorhandensein von Nullen sagt uns, in welchen Zahlensystemen wir erfolgreich sein werden. Aber hier ist das Problem: Unter dem Gesichtspunkt der Suche nach Primzahlen ist eine Einheit mit Nullen für uns überhaupt nicht interessant, da sie garantiert durch die Basis des Zahlensystems geteilt wird, das uns alle diese Nullen nach eins gibt. Sie müssen also die Teilbarkeit anderer Zahlenklassen untersuchen. Ist es logisch? Genau das werden wir tun.

Können wir die Teilbarkeitstheorie ausprobieren?

Zuvor haben wir uns mit den Regelmäßigkeiten der Resttabellen für die Divisionsoperation vertraut gemacht, die uns relativ vertraut sind. Die Muster erwiesen sich als unterhaltsam, haben aber immer noch das gleiche Problem - sie geben uns keinen schnellen Algorithmus zur Überprüfung der Einfachheit. Für einen solchen Test müssen wir, wie im Test nach der Fermat-Formel, die Zahlen sehr stark erhöhen und dann den Rest der Division des Ergebnisses durch die untersuchte Zahl finden. Oder durchlaufen Sie einfach alle Überreste mit der „Eck“ -Methode (natürlich vor dem thermischen Tod des Universums). Hier sind die Daten - der Vorgang des Erhöhens auf eine Leistung mit dem Finden des Restes dauert 15 Minuten auf einem Kern für die Anzahl der Bestellungen $$$2 ^ {100000}$ . Mit einer 1000-fachen Vergrößerung der Zahlengröße erhalten wir eine quadratische Vergrößerung (plus Logarithmen, aber das ist nicht so viel), mindestens 1.000.000-fach, aber in Wirklichkeit viele Millionen-fach. Angenommen, wir erhalten als Ergebnis eine Million Stunden für einen Test. Dies sind ungefähr 40.000 Tage oder merklich mehr als hundert Jahre. Wenn wir die Ausführung des Tests bis ins kleinste Detail optimieren und ihn unter Berücksichtigung aller Merkmale der Prozessorarchitektur durchführen, erhalten wir möglicherweise statt hundert Jahren 10. Auf 10 Kernen - 1 Jahr. Für 1000 Kerne - 4 Tage. Dies ist jedoch nur ein probabilistischer Test, da es Maskeraden als einfache zusammengesetzte Zahlen gibt. Sie müssen also noch eine Überprüfung durchführen. Wichtiger ist jedoch die Tatsache, dass die Anzahl der Kandidaten Millionen beträgt. Nach all den möglichen Filtrationen wird es auch viele davon geben. Daher spielt die Welt immer noch mit zehn Megabyte.

Aber wir haben ein Werkzeug. Die Resttabelle funktioniert auch für andere Arten von Zahlen. Nehmen Sie zum Beispiel die Mersenne-Nummern. In der Binärdatei ist es nur eine Folge von Einheiten. Was hindert uns daran, eine Folge von Einheiten anstelle einer Folge von Nullen zu untersuchen? Ja, nichts verhindert. Und es stellt sich heraus, dass unsere Methode für eine solche Sequenz recht gut funktioniert und eine Reihe zuvor identifizierter Muster darin erhalten bleiben. Hier ist das Ergebnis für die Nummer 7:



Wie wir sehen können, ist die Primzahl 7 in allen Zahlensystemen (mit Ausnahme von Vielfachen von sieben) ein Teiler der Mersenne-Zahlen. Das heißt, in fast jeder Zeile gibt es eine Null, die uns über die Teilbarkeit von Zahlen der Form 111 ... 111 (im Binärsystem) durch 7 sagt. Wenn wir also mit dem Binärzahlensystem arbeiten, sehen wir, dass die Zahl 7 alle Mersenne-Zahlen, die Länge, teilt Dies ist ein Vielfaches von 3. Dieses Ergebnis ist auch ohne Resttabelle offensichtlich - die Zahl 7 in binärer Form besteht aus drei Einheiten (111), sodass die Binärzahl aus drei Einheiten geteilt wird. Und wenn es mehr Einheiten gibt, sieht die Aufteilung folgendermaßen aus:

111111 | 111 ------ 111 1001 111 111 111 

Das heißt, wir setzen einfach sieben (in binärer Form) unter die Dividende. Und wie oft passen die sieben - so viele dreifache Einheiten in einer teilbaren Zahl. Wenn darin die Anzahl der Einheiten kein Vielfaches von drei ist, dann ist eine solche Anzahl nicht durch 7 teilbar. Dies ist jedoch nur dann offensichtlich, wenn wir Zahlen mit identischer Struktur untersuchen (7 und 63, wie im Beispiel). Und wenn die Struktur der Zahlen komplizierter ist, hilft uns eine Tabelle mit Residuen. Wir erhalten also ganz einfach ein ähnliches Ergebnis, jedoch mit einer etwas längeren Teilungsperiode. Unten ist ein Beispiel für die Zahl 11 (die Zahl ist bereits dezimal):



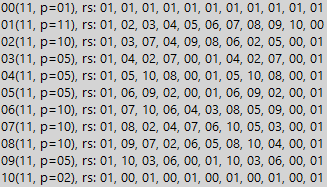
Wir sehen, dass im binären System der Abstand zu Null (Teilbarkeitsperiode) für die Zahl 11 10 ist. Das heißt, jede Mersenne-Zahl, die 10k Einheiten enthält, wobei k eine ganze Zahl größer als Null ist, ist notwendigerweise durch 11 teilbar. Es kann leicht bewiesen werden, dass der Rest einfach ist Zahlen verhalten sich bis auf die Größe des Zeitraums natürlich genau gleich. Aber für die Verbindung ist die Situation wieder weniger harmonisch. Unten sehen wir ein Beispiel für die Nummer 8:



Anscheinend kann 8 Mersenne-Zahlen nicht in binärer Form teilen. Hier im Ternär - bitte, aber die Mersenne-Zahlen bestehen nur aus Einheiten in binärer Form. Ähnlich verhält es sich mit anderen zusammengesetzten Zahlen - sie haben alles auf unterschiedliche Weise. Das schlanke und symmetrische Bild für Primzahlen wiederholt sich nicht für zusammengesetzte. Aber für uns ist genau das Einfache wichtig, denn wenn die Zahl in eine Primzahl unterteilt ist, ist es absolut kein Problem, wenn sie auch in eine Verbindung unterteilt wird, die dieses Einfache enthält. Wenn die Zahl jedoch nicht in eine einfache Zahl unterteilt ist, ist es unmöglich, sie in eine Verbindung mit einer so einfachen Zahl zu unterteilen. Wir sollten uns also nur für Primzahlen interessieren.

Lassen Sie uns nun zusammenfassen. Wir wissen, dass Mersenne-Zahlen in Primzahlen unterteilt sind und dass Mersenne-Zahlen für die Teilbarkeit eine Anzahl von Einheiten benötigen, die ein Vielfaches der Teilbarkeitsperiode der untersuchten Zahl ist. Wir wissen aber auch, dass Kandidaten für Mersenne-Primzahlen nur solche sind, bei denen die Anzahl der Einheiten auch eine Primzahl ist. Das heißt, dieser Betrag ist nur in eine Einheit und in sich selbst unterteilt. Daher die Schlussfolgerung - wir brauchen eine solche Primzahl, deren Teilbarkeitsperiode gleich der Länge der Mersenne-Zahl ist. Wenn wir für eine gewisse Länge der Mersenne-Zahl keinen Teiler mit einer geeigneten Periode gefunden haben, haben wir eine Mersenne-Primzahl vor uns. Es scheint einfach.

Aber es beginnen weitere Schwierigkeiten. Wie finde ich eine Nummer, deren Periode mit der Länge der Mersenne-Nummer übereinstimmt? Um diese Frage zu beantworten, müssen Sie eine bescheidene Aufgabe lösen - mit einfachen Mitteln einen Weg finden, um den Zeitraum für eine beliebige Primzahl herauszufinden. Im Moment können wir nur eine Ecke teilen oder an einer bestimmten Stelle mit einer Formel mit großen Graden stoßen. Wenn wir jedoch den Zeitraum ohne lange Berechnungen berechnen könnten, würden wir schnell den richtigen Teiler finden oder sicherstellen, dass es keinen in der Natur gibt. Genau die gleiche bescheidene Aufgabe erwartet uns bei der Untersuchung der Teilbarkeit von Zahlen der Form 1000 ... 000. Die Zeit der Teilbarkeit ist also in jeder Hinsicht sehr wichtig.

Wie finde ich eine Periode?

Hier eilen uns Quantencomputer zu Hilfe. Es war einmal, seit einiger Zeit, ein gewisser Kenner der Quantenphysik namens Shor, der vorschlug, die Periode mit Hilfe eines Quantencomputers genau zu finden. Tatsächlich gibt ein Quantencomputer nur einen Zwischenwert an, von dem ein gewöhnlicher Computer dann eine Periode empfängt, aber der Punkt ist nicht der, sondern dass die Mathematik ohne einen Quantencomputer die Periode nicht berechnen kann. Bei der Berechnung des Zeitraums haben wir jedoch die Möglichkeit, den Wert des Restbetrags genau in der Mitte des Zeitraums genau zu berechnen. Warum wird das benötigt? Für die Tatsache, dass Sie daraus Faktoren erhalten können, die notwendigerweise einen bestimmten Wert enthalten, der ein Vielfaches des Teilers der untersuchten Zahl ist. Dies erfolgt durch Addieren zum Rest der Einheit und Subtrahieren der Einheit. Die resultierenden zwei Zahlen können durch einen schnellen Algorithmus übersprungen werden, um den größten gemeinsamen Teiler mit der untersuchten Zahl zu finden. In mindestens einem Fall erhalten wir den Teiler der untersuchten Zahl. Es stimmt, nicht alles ist so perfekt, denn wie wir im Beispiel der Tabelle für Primzahlen gesehen haben, wird in der Mitte der Zeile häufig eine Zahl zu der untersuchten Zahl hinzugefügt (N-1). In dieser Form erhalten wir:

$$

$$N-1 + 1 = N$$

$$

$$N-1-1 = N-2$$

Daraus folgt, dass wir in einem Fall die untersuchte Zahl selbst haben und es keinen Sinn macht, den größten gemeinsamen Faktor zu berechnen, und im zweiten Fall haben wir garantiert, dass es keine gemeinsamen Teiler mit der untersuchten Zahl gibt. Es gibt keine gemeinsamen Teiler, da diese Zahl nur 2 weniger als die untersuchte Zahl ist. Dies bedeutet, dass unabhängig davon, welche Zahl in die untersuchte Ganzzahl passt (wäre ihr Teiler), wenn wir sie von der untersuchten Zahl abziehen, wir eine garantierte niedrigere Zahl erhalten Wert als $$$N-2$ oder unter Verwendung der Formeln:

$$

$$N / x = k$$

$$

$$(N-x) / x = k-1$$

$$

$$N-x <N-2 \ Rightarrow x> 2 \; \ & \; (N-2) / x \ ne m$$

Hier ist N eine ungerade Testzahl (ungerade, weil ein Vielfaches von zwei durch zwei teilbar ist und wir nicht durch irgendetwas teilen müssen), x ist ein Teiler von N, k ist das gesamte Ergebnis der Division $$$N / x$ , m ist das gesamte Ergebnis der Teilung $$$(N-2) / x$ . Das heißt, wir müssen manchmal das Zahlensystem ändern und den Quantencomputer bitten, eine neue Periode zu finden, in der Hoffnung, dass es in der Mitte eine geeignetere Zahl gibt. Eine Plusbeschränkung ist die obligatorische Parität des Periodenlängenwerts. Dies ist jedoch nicht so beängstigend, da ein Quantencomputer in jedem Fall die benötigte Länge (oder mehrere Längen) viel schneller berechnet als der thermische Tod des Universums im Gegensatz zu anderen Algorithmen.

Die Berechnung des Zeitraums für das Erhalten von Zahlenteilern unterscheidet sich zwar geringfügig von der Suche nach einfachen Teilern. Trotzdem können wir hier anhand der übrig gebliebenen Tabellen etwas hinzufügen. Die Tabellen zeigen also, dass die Mitte von Zeilen mit gerader Länge normalerweise eine Zahl ist, die die folgende Bedingung erfüllt:

$$

$$r ^ 2 \ pmod N = 1$$

Hier ist r der gewünschte Rest und N die untersuchte Zahl. Es stellt sich also heraus, dass es nicht erforderlich ist, nach einer Periode zu suchen, um Teiler einer Zahl zu erhalten, da eine Periode durchsucht wird, um den Rest r zu finden und dann eine davon zu addieren und davon zu subtrahieren. Das heißt, Sie können diesen Rest sofort finden, der die obige Bedingung erfüllt. Die Suche nach diesem Wert ist ebenfalls nicht trivial. Aber vielleicht kann ein Quantencomputer für so etwas eingesperrt werden? Experten im Quantencomputer müssen verstehen, wie viele Qubits dafür benötigt werden (Qubits sind die Papageien, die die "Leistung" eines Quantencomputers messen). Obwohl Sie vielleicht auf einen Quantencomputer verzichten können. Dazu müssen Sie nur verstehen, welche Muster nützlich sein werden. Einige der Muster sind in den Residuentabellen sichtbar, aber der Rest der Leser muss es selbst herausfinden, und dann werden Sie definitiv die RSA-basierte Kryptographie knacken. Es stimmt, es gibt ein paar Schwierigkeiten - zuerst müssen Sie diese nützlichen Muster finden, und dann ... Dann zahlen sie Ihnen möglicherweise kein Geld. Erstens geben Preise für große Primzahlen, nicht für das Hacken von RSA. Und zweitens: Überlegen Sie selbst, wie viele seriöse Organisationen auf der Welt daran interessiert sind, die Daten anderer Personen auf diese Weise abzufangen. Und einige FSB (CIA, Mossad, Mi-5, nur die Mafia) haben herausgefunden, dass Sie etwas wissen. Ratet mal, was mit dir passieren wird? Daher handeln Sie weiterhin ausschließlich auf eigene Gefahr und Gefahr.

Das Quantenthema selbst ist insofern sehr interessant, als es Quantenunsicherheit, Vakuumschwankungen und anderen Quantendarwinismus enthält. Wie kann das alles erklärt werden? Um ehrlich zu sein, weiß ich es nicht, aber ich sehe eine Analogie zu den restlichen Tabellen. Wenn zum Beispiel jemand die Werte in der Resttabelle beobachtet und die zuvor erwähnten Muster nicht kennt, gibt es für ihn nur ein gewisses Rauschen in der Tabelle, bei dem sich die Zahlen auf zufällige Weise ändern, wie etwa einige Schwankungen im Vakuum. Wenn Sie jedoch verstehen, dass wir nur denselben Algorithmus auf verschiedene Paare von „untersuchten Sequenznummern“ anwenden, wird all dieser kochende Brei aus den Zahlen sofort verständlich. Auf die gleiche Weise wird deutlich, warum unter den zahlreichen möglichen Werten für das Ausfüllen der Tabelle nur noch genau definierte Werte enthalten sind. Aber bis wir die „Interaktion“ der Sequenz mit der untersuchten Zahl erhalten, können wir den Inhalt der Tabelle nicht vorhersagen. Genauer gesagt ist jede Füllung gleichermaßen wahrscheinlich. Aber nach der „Interaktion“ wird alles streng logisch, aus der ebenso wahrscheinlichen wird eine einzige Wahrscheinlichkeit für nur eine Option geboren. Und das nicht, weil ein bestimmter Darwinismus funktioniert, sondern nur, weil ein bestimmter Algorithmus auf bestimmte Eingabedaten angewendet wird. Wenn Sie den Algorithmus nicht kennen, scheinen die Zeilen in der Tabelle tatsächlich im Darwin-Stil zu sein. Und wenn Sie wissen - alles ist sehr einfach. Vielleicht ist es in der Quantenphysik notwendig, nicht nur nach Teilchen zu suchen, sondern auch nach einem Algorithmus für ihre „Teilung“?

Und noch einmal über die Zeit

Der Zeitraum ist jedoch für uns sehr wichtig. Ja, so werden sie Ihnen in der Hotline zu den brennenden Problemen der Mathematik antworten. Wie oben gezeigt, ermöglicht die Kenntnis der Periode zu verstehen, ob eine Zahl Teiler hat oder auf andere Weise, ob es sich um eine Primzahl handelt. Deshalb fahren wir über den Zeitraum fort. Bisher kennen wir eine Reihe von Periodeneigenschaften (Eindeutigkeit von Werten, Symmetrie mit einer geraden Länge usw.), aber wir wissen nicht, wie wir ihre Länge bestimmen sollen. Obwohl es eine obere und eine untere Grenze gibt, kann der Zeitraum nicht länger sein als die untersuchte Zahl minus eins, und der Zeitraum kann auch nicht kürzer sein als die Wachstumsperiode der Basis des Zahlensystems, bis die untersuchte Zahl überschritten wird (für sieben ist es 3, für 11 ist es 4 usw.). .). Sie können versuchen, die aus den untersuchten Tabellen bekannten Gesetze anzuwenden und neue abzuleiten. Bisher gibt es hier jedoch einige Richtungen, von denen die meisten nicht zum Erfolg führen, obwohl Sie es erst wissen, wenn Sie sie jeweils ausprobieren.

Der vielversprechendste Weg ist daher die Schaffung einer verbesserten Teilbarkeitstheorie. Anhand der charakteristischen Folgen von Resten lassen sich die Teilbarkeitsgesetze vieler Zahlenklassen aufzeigen. Bisher wurden nur zwei Klassen gezeigt (Mersenne-Zahlen und Zahlen, die den Graden des Zahlensystems entsprechen), aber in Wirklichkeit gibt es unendlich viele davon. Wie verarbeite ich Wissen über alle Zahlenklassen? Nur in massiven Parallelarbeiten und nicht in Form von Eisenlufterhitzern, sondern in Form von Menschen, die an einer so großen Aufgabe zusammenarbeiten. Das ideale Ergebnis wäre die Schaffung einer allgemeinen Teilbarkeitstheorie aller Zahlenklassen. Dies ist für den Anfang, und dann wird die Teilbarkeit von Polynomen und anderer Algebra gehen. Aber sollten wir eine so wunderbare Ansammlung menschlicher Gedanken über die Aufgabe erwarten, Primzahlen zu finden? Ich vermute nicht. Deshalb brauchen wir leider wieder andere Wege.

Theoretisch gibt es so einen

Wenn wir alternative teilbare Sequenzen untersuchen, einschließlich unterschiedlicher Werte, stellen wir fest, dass die Teilungsperiode solcher Sequenzen ein Vielfaches der Länge der sich wiederholenden Fragmente der Sequenzen vergrößert. Unten sehen Sie ein Beispiel für eine teilbare Folge der Form 1010 ... 1010, bei der sich Null und Eins periodisch ändern. Die angegebene Reihenfolge ist immer in die Basis des Zahlensystems unterteilt. In diesem Fall ist die Einfachheit des Beispiels zum Studieren der Zahlen der periodischen Klasse nur für uns wichtig, sodass wir die Teilbarkeit „durch Konstruktion“ nicht berücksichtigen.





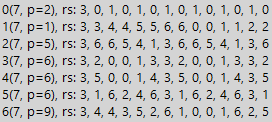
Hier sehen wir zwei Tabellen für die Nummer 7 und die oben angegebene Reihenfolge, eine ist normal und die zweite Tabelle wird mit 3 multipliziert. Aus den zuvor identifizierten Mustern in diesem Beispiel gibt es noch weniger, aber für Zahlensysteme auf den Basen 1 und 6 sehen wir dennoch Erhöhen Sie die Dauer des Zeitraums auf $$$2 * N-2$ . Und für multipliziert mit 3 Tabellen sehen wir einen Teilbarkeitsverlust für die Grundlagen der Zahlensysteme 2 und 5, der an sich ziemlich unterhaltsam ist (die Eigenschaft der Teilbarkeit hat sich durch Multiplikation geändert). Aber wichtiger als das. Es ist wichtig, die Möglichkeit zu verstehen, Teilbarkeitstabellen auf beliebige Sequenzen anzuwenden. Aber warum brauchen wir irgendwelche Sequenzen? Zum Beispiel, um die Mindestteilbarkeitsdauer zu erhöhen.

Wenn die Mindestdauer verlängert werden kann, können wir sehr einfach mit der Konstruktion von Primzahlen fortfahren. Ja, Primzahlen können nicht berechnet, sondern mathematisch konstruiert werden. Wenn die Periode lang ist, teilt eine kleine Zahl eine große. Wenn alle Zahlen große Perioden haben, können Teiler für große Zahlen nur kleine Zahlen sein. Was gibt es? Dies ermöglicht es, alle Teiler einer großen Zahl durch eine einfache Suche zu finden. Da kleine Zahlen große Zahlen teilen, hilft die Größe dieser kleinen Zahlen unseren Computern, das Problem zu lösen, das sie mit großen Teilern nicht lösen können. Daher wird die weitere Richtung der Suche nach Primzahlen klar - wir müssen eine Sequenz finden, die uns große Mindestperioden gibt. Warum das Minimum? Da wir immer noch nicht wissen, wie man eine Periode berechnet, ohne alle Residuen aufzuzählen oder auf eine Potenz zu erhöhen, und wir daher nicht einfach eine ausreichend lange Periode finden können, wenn sie größer als das Minimum ist, kennen wir die minimale Periode einfach aus der Analyse der Resttabellen, das heißt, wir müssen sie nicht berechnen . Nun, wenn wir die Sequenz finden, die wir brauchen (und nur dafür können wir die Analyse vieler Klassen solcher Sequenzen verwenden), wählen wir einfach die Länge der Sequenz aus, die nicht in eine der uns bekannten Mindestperioden passt. Das heißt, wir werden eine so große Anzahl aufnehmen, die offensichtlich keine Teiler hat. Und wenn es groß ist, erwartet uns ein Preis. Gleichzeitig werden wir nicht an mehr als den Mindestperioden interessiert sein, da sie bereits sehr große Zahlen teilen, die wir später erreichen werden.

Sie müssen nur noch die richtige Reihenfolge finden. Wer wird es nehmen? Aber selbst wenn wir es nicht finden, können Sie bei der oben genannten Verschlüsselung mit alternativen Sequenzen der Chiffre einen weiteren Begriff hinzufügen, der die kryptografische Stärke erhöht. Jetzt müssen Chiffriercracker die von uns gewählte Sequenz erraten, deren Anzahl unendlich sein kann. Um pseudozufällige Sequenzen zu erzeugen, erhalten wir außerdem die Wiederholbarkeit der Werte in der Reihe der Residuen und nicht nur in der Reihe der Bruchperiode.

Und zum Schluss die Preise!

Die Electronic Frontier Foundation ist bereit, jedem zuerst 150.000 USD und dann weitere 250.000 USD zu zahlen. Insgesamt - 400.000 US-Dollar . Würde dich das nicht stören? Dann auf den Punkt! Aber die Sache ist einfach - Sie müssen eine Primzahl von einhundert Millionen Dezimalstellen finden. Dies sind ungefähr 300 Millionen Bit oder 40 Megabyte. Nur noch übrig, um den aktuellen Rekord viermal zu überholen. Und dann brauchen Sie eine Milliarde Dezimalstellen lang. Das sind schon 400 Megabyte. Und das alles für zwei Zahlen - 400 Tausend für immer grüne Dollar.

In der Tat sind dies keine so schrecklichen Zahlen. Wenn wir nun davonkommen könnten, den Rest der Division großer Grade durch die untersuchte Zahl zu berechnen ... Für einfache Sequenzen der Form 100 ... 00 und 111 ... 111 ist der Grad notwendigerweise vorhanden. Aber vielleicht gibt es Sequenzen, für die die Formel zur Berechnung des i-ten Elements einer Reihe von Resten einfacher ist? Oder Sie finden wirklich eine Sequenz mit einer großen Mindestdauer. Welchen Zeitraum brauchen wir schließlich? Nur 300 Millionen (in binärer Form). Wenn eine bestimmte Sequenz einen Mindestzeitraum der Form 100 * N ergibt, wobei N die untersuchte Zahl ist, reichen bis zu 3 Millionen Zahlen aus, um eine Zahl im Wert von 150.000 USD zu finden. Und bis zu 30 Millionen für eine 250.000-Dollar-Zahl. Und jetzt, wenn eine kurze Periode in einer sehr großen Anzahl auftreten kann (für die Sequenzen 100..00 und 111 ... 111), haben wir keine einfachen Möglichkeiten, sie zu finden. Aber es gibt Hoffnung und alles hängt von der erfolgreichen Wahl der Suchrichtung ab. Das Durchlaufen der Sequenzen nacheinander ist anscheinend für eine Person nicht realistisch, aber Sie können die Menge ausprobieren.

Nun, wenn Sie die erforderlichen Zahlen gefunden haben, erwartet Sie ein wenig Bürokratie. Zuerst müssen Sie einen Artikel in einer mathematischen Zeitschrift in den USA oder England oder Kanada oder Australien veröffentlichen, und die Zeitschrift sollte aus der von der Electronic Frontier Foundation (EFF) angegebenen Liste stammen (dies sind sehr seriöse Zeitschriften). In dem Artikel müssen Sie beweisen, dass Ihre Methode es wirklich ermöglicht, die gewünschte Primzahl zu finden. Anschließend senden Sie einen Glücksbrief an die EFF (an eine bestimmte Adresse), in dem Sie auf den veröffentlichten Artikel verweisen und auf Bestellungen der EFF warten. Bestellungen können sich darauf beziehen, alles zu überprüfen, was Sie getan haben, um die Nummer zu finden. Es sollte keine Geheimnisse oder illegalen oder zweifelhaften Handlungen geben. Und das ist alles danach - Ihr Preis.

Welche Hinterhalte können Sie auf Ihrem Weg erwarten? Nun, für den Anfang - um eine Primzahl zu finden und keine Fehler bei der Suche zu machen. Als nächstes müssen Sie in ein solides Tagebuch schreiben. Da das Magazin solide ist, ist die übliche Reaktion der Herausgeber auf den Brief des nächsten Erfinders der Perpetual Motion Machine folgende:

- Was? Noch ein Freak? In den Korb!

Es ist jedoch möglich, dass Sie Erfahrung im Schreiben von Artikeln haben und dieses Problem problemlos bewältigen können. Und dann finden Sie einen Scheck. Ich weiß nicht, wie Ihre Beweise von EFF untersucht werden, aber sie schreiben, dass sie an allem, an allem interessiert sein können. Es ist besonders interessant, wenn die EFF-Ziele nicht mit dem von Ihnen angegebenen Ergebnis übereinstimmen. Sie erklären daher das Ziel, Methoden für die Verwendung von PCs zu entwickeln, um sie für Remotecomputer von Drittanbietern vorübergehend remote zu verwenden. Der vorherige Preis wurde nur für die Erstellung und Förderung des Programms vergeben, das von Freiwilligen heruntergeladen und damit die notwendigen Terraflops zum Schleifen von Primzahlen bereitgestellt wurden.Wie sich EFF auf die Berechnung einer Primzahl ohne Massen-Terraflops bezieht - weiß ich nicht. Theoretisch gibt es keine Einschränkungen hinsichtlich ihrer Anforderungen, so dass Erfolg durchaus möglich ist.

Nachdem Sie die beiden angegebenen Phasen durchlaufen haben (und nicht vergessen haben, die erforderlichen Nummern in der Nullphase zu finden), geben Sie die Bank und die Kontonummer an, bei der der Preis an Sie fällt. Eine große Summe. Sie kümmern sich auf eigene Kosten um die Steuer.

Anstelle eines Nachworts

Es war einmal, als Pierre Fermat, kein Mathematiker, viele Muster für die Zahlentheorie entdeckte. Der Mann fragte sich nur, nun, es war Freizeit zur Verfügung. Und hier haben Sie die Erfolge, an die Sie sich noch erinnern. Ein anderes Beispiel ist Evarist Galois. Er nahm im Alter von 16 Jahren Mathematik auf und starb im Alter von 20 Jahren in einem Duell. 4 Jahre lang versuchte er, viele Mathematiker für seine Funde zu interessieren, aber es gelang ihm nicht. Nach dem Tod wurde seine Arbeit dennoch gewürdigt, und ihnen verdanken wir die Schaffung eines solchen Zweigs der Mathematik wie der Gruppentheorie sowie die Entwicklung der Algebra. Wieder - es war interessant für einen Menschen, die Sterne zu finden, aber die Werke nach den Regeln zu ordnen, war nichts für ihn. Glücklicherweise wurde seine Arbeit von anderen formalisiert. Und ein anderes Beispiel - George Cantor, der über die bekannten Konzepte der Menge und ihres Elements nachdachte, leitete die Theorie Ende des 19. Jahrhunderts ab.welche herausragenden Mathematiker sich bereit erklärten, es wert zu sein, die Grundlage der Königin der Wissenschaften zu werden.

Warum all diese Geschichten? Wie Herr Obama immer sagte: "Sie können!" Ja, dieser amerikanische Slogan eignet sich gut für begeisterte Menschen. Trotz der heutigen Entwicklung der Wissenschaft ist sie nicht vollständig, nicht perfekt und es gibt Stellen darin, an denen der Fuß eines echten Wissenschaftlers nicht getreten ist. Lassen Sie uns also unsere Neugier einschalten und versuchen, nach solchen ungehinderten Wegen zu suchen, und was ist, wenn Sie Erfolg haben?