Der neue Beweis löst die Approximation von Zahlen wie pi

Die alten Griechen waren daran interessiert, ob es möglich ist, irrationale Zahlen grob in Brüchen auszudrücken. Zwei Mathematiker haben die langjährige Duffin-Schaffer-Hypothese bewiesen und eine erschöpfende Antwort gegeben.

Die binäre Notation π ist unendlich. Aber eine unendliche Anzahl von Brüchen kann sich dieser Zahl mit immer größerer Genauigkeit nähern.

Tiefe Einbrüche auf der Zahlenlinie sind nicht so uneinnehmbar, wie es scheint. Dies ist eine der Konsequenzen neuer aussagekräftiger Beweise dafür, wie sich komplexe Zahlen für einfache Näherungen eignen.

Der Beweis löst das Problem von vor fast 80 Jahren, bekannt als die Duffin-Shaffer-Hypothese. Somit gibt es eine endgültige Antwort, die Mathematiker seit der Antike beschäftigt: Unter welchen Bedingungen ist es möglich, unendlich lange irrationale Zahlen - wie pi - mit einfachen Brüchen vom Typ 22/7 darzustellen? Der Beweis belegt, dass die Antwort auf diese eher allgemeine Frage auf einer einzigen Berechnung beruht.

"Es gibt ein einfaches Kriterium dafür, ob Sie fast jede Zahl oder praktisch keine Zahl annähern können", sagte James Maynard von der Universität Oxford, Co-Autor des Beweises, den er zusammen mit Dimitris Cuculopoulos von der Universität von Montreal gemacht hat.

Mathematiker haben seit mehreren Jahrzehnten den Verdacht, dass dieses einfache Kriterium der Schlüssel zum Verständnis ist, wann man eine gute Annäherung erhalten kann - aber sie konnten es nicht beweisen. Kukulopoulos und Maynard konnten dies erst tun, nachdem sie dieses Zahlenproblem in Bezug auf die Verbindungen zwischen Punkten und Linien des Graphen neu formuliert hatten - ein grundlegender Perspektivwechsel.

"Ich würde sagen, sie waren zuversichtlich genug (und das war offensichtlich gerechtfertigt), den gewählten Weg einzuschlagen", sagte Jeffrey Waaler von der University of Texas in Austin, der an den frühen Ergebnissen im Zusammenhang mit der Duffin-Schaffer-Hypothese beteiligt war. "Großartige Arbeit."

Arithmetischer Äther

Mit rationalen Zahlen ist alles einfach. Sie enthalten Zahlen zum Zählen von Objekten und alle anderen Zahlen, die in Brüchen geschrieben werden können.

Aufgrund dieser Fähigkeit, aufgeschrieben zu werden, sind uns rationale Zahlen am besten bekannt. Unter allen reellen Zahlen gibt es jedoch nur wenige rationale. Die meisten Zahlen sind irrational mit unendlicher Dezimalschreibweise und können nicht in Brüchen geschrieben werden. Einige von ihnen erwiesen sich als wichtig genug, um eine symbolische Notation zu verdienen - pi, e, √2. Der Rest kann nicht einmal angerufen werden. Sie sind überall, aber unerreichbar - wie ein arithmetischer Äther.

Vielleicht ist es deshalb natürlich zu denken - wenn wir irrationale Zahlen nicht genau ausdrücken können, wie nahe können wir ihnen kommen? Dies ist ein Bereich der rationalen Annäherung. Mathematiker der Antike erkannten, dass das schwer fassbare Verhältnis von Umfang zu Durchmesser mit der Fraktion 22/7 recht gut angenähert werden kann. Später entdeckten Mathematiker eine noch genauere und fast dieselbe komprimierte Annäherung an pi: 355/113.

"Pi zu schreiben ist sehr schwierig", sagte Ben Green aus Oxford. "Die Leute haben versucht, die genaueste Annäherung an pi zu finden, und eine der gebräuchlichsten Methoden, dies zu tun, war die Verwendung rationaler Zahlen."



1837 entdeckte der Mathematiker Peter Gustav Lejeune von Dirichlet eine Regel, die uns sagt, wie genau irrationale Zahlen mit rationalen Zahlen angenähert werden können. Die Annäherung ist leicht zu finden, wenn Sie den genauen Wert des Fehlers nicht einstellen. Dirichlet bewies jedoch die Existenz einer klaren Beziehung zwischen Brüchen, irrationalen Zahlen und den Fehlern, die sie trennen.

Er bewies, dass es für jede irrationale Zahl unendlich viele Fraktionen gibt, die sich ihm immer näher nähern. Genauer gesagt beträgt der Fehler jedes Bruchs nicht mehr als 1 geteilt durch das Quadrat des Nenners. Zum Beispiel drückt der Bruch 22/7 pi ungefähr mit einer Genauigkeit von 1/7 ² oder 1/49 aus. Die Fraktion 355/113 ist nicht weiter von pi entfernt als 1/113 ² oder 1/12 769. Dirichlet hat bewiesen, dass es unendlich viele Fraktionen gibt, die mit zunehmendem Nenner immer näher an pi heranrücken.

"Eine erstaunliche und bemerkenswerte Sache ist die Fähigkeit, eine reelle Zahl grob durch einen Bruch auszudrücken, wobei ein Fehler nicht größer als eins geteilt durch das Quadrat des Nenners ist", sagte Andrew Granville von der Universität von Montreal.


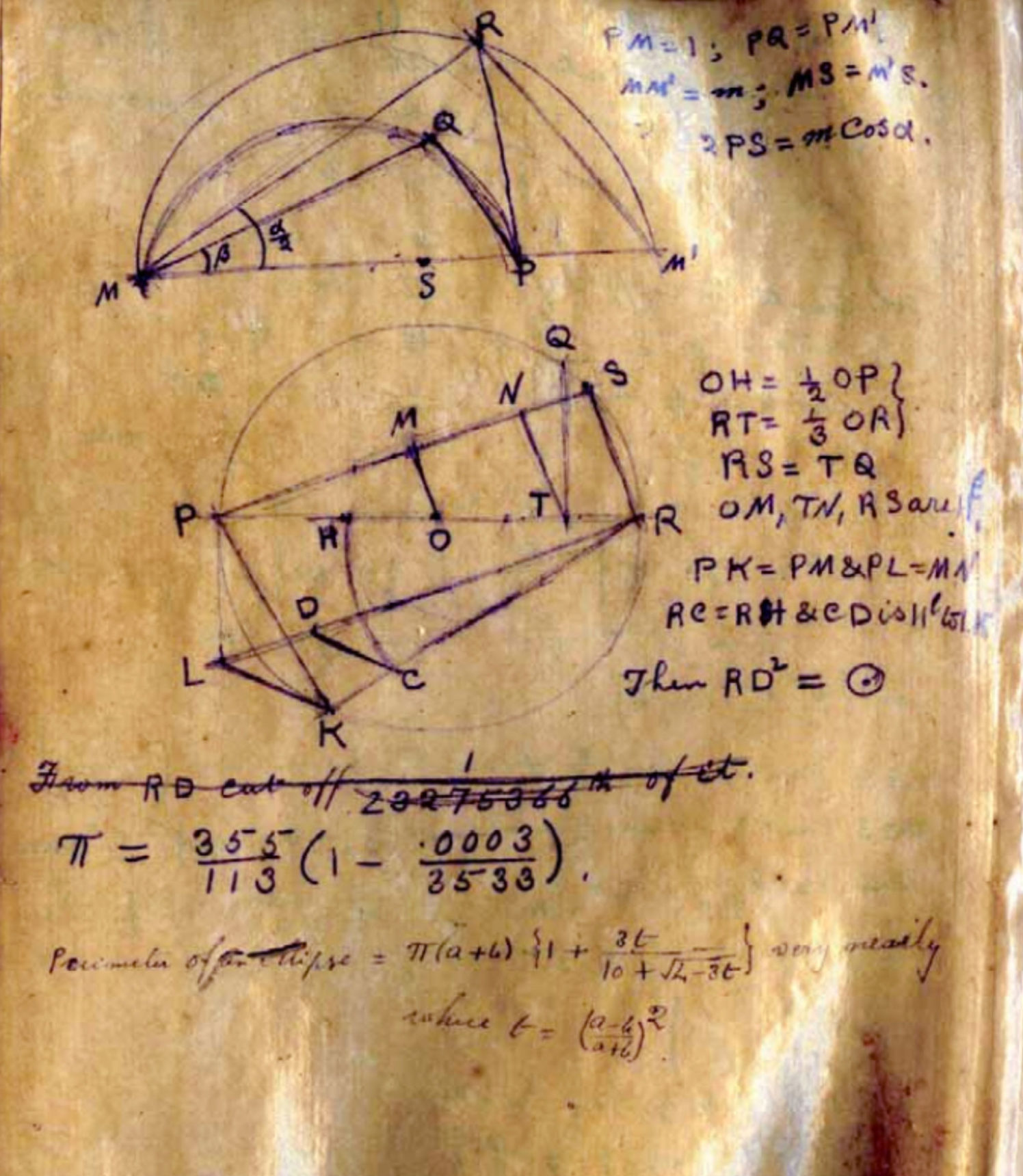Im Manuskript von 1913 verwendete der Mathematiker Srinivasa Ramanujan Iyengor die Fraktion 355/113 als rationale Annäherung an pi.

Dirichlets Entdeckung war eine begrenzte Aussage über rationale Approximation. Es heißt, dass Sie für jede irrationale Zahl unendlich viele Brüche finden können, wenn Sie eine ganze Zahl als Nenner verwenden können, und Sie sind mit dem Fehler in der Größe ihres inversen Quadrats zufrieden. Aber was ist, wenn die Nenner zu einer (unendlichen) Teilmenge von ganzen Zahlen gehören müssen, zum Beispiel zur Menge der Primzahlen oder zur Menge der vollständigen Quadrate ? Was ist, wenn der Approximationsfehler 0,00001 betragen oder einen anderen Wert haben soll? Werden Sie in der Lage sein, unter solchen Bedingungen unendlich viele Näherungsfraktionen zu finden?

Die Duffin-Shaffer-Hypothese ist ein Versuch, die allgemeinste Plattform für die Arbeit mit rationalen Näherungen zu schaffen. 1941 stellten die Mathematiker R.D. Duffin und A.S. Schafer stellte das folgende Szenario vor. Wählen Sie zunächst eine endlose Liste von Nennern. Es kann alles sein, was Sie wollen: ungerade Zahlen, durch 10 teilbare Zahlen, Primzahlen.

Wählen Sie dann für jede Zahl in der Liste aus, wie genau Sie die irrationale Zahl approximieren möchten. Die Intuition sagt uns, dass wir mehr Möglichkeiten zur Annäherung haben, wenn wir ausreichend große Fehler wählen. Wenn Sie eine kleine Fehlergröße wählen, wird dies schwieriger. "Jede Sequenz reicht aus, wenn noch genügend Platz vorhanden ist", sagte Kukulopoulos.

Angesichts der ausgewählten Parameter - einer Folge von Zahlen und eines bestimmten Fehlers - stellt sich nun die Frage: Ist es möglich, unendlich viele Brüche zu finden, die sich allen irrationalen Zahlen annähern?

Die Hypothese bietet eine mathematische Funktion zur Bewertung dieser Frage. Ihre Parameter dienen als Eingabe. Das Ergebnis kann eine von zwei Optionen sein. Duffin und Schaffer schlugen vor, dass diese beiden Optionen genau der Frage entsprechen, ob Ihre Sequenz fast alle irrationalen Zahlen mit der erforderlichen Genauigkeit approximieren kann oder praktisch keine davon („praktisch“ wird erwähnt, da es für jeden Satz von Nennern immer eine kleine Zahl gibt isolierte irrationale Zahlen, die gut genug angenähert werden können oder nicht).

„Man bekommt fast alles oder fast nichts. Es gibt keine Zwischenoptionen “, sagte Maynard.

Dies war eine äußerst allgemeine Aussage, die versuchte, die Annäherung durch rationale Zahlen entlang und quer zu charakterisieren. Das von Duffin und Schaffer vorgeschlagene Kriterium schien den Mathematikern richtig zu sein. Um jedoch zu beweisen, dass die Binärausgabe der Funktion alles enthält, was Sie benötigen, um zu verstehen, ob Ihre Approximation funktioniert oder nicht, war dies viel schwieriger.

Doppelzählung

Der Beweis für die Duffin-Schaffer-Hypothese besteht darin, zu verstehen, welchen Nutzen Sie aus jedem der Ihnen zur Verfügung stehenden Nenner ziehen. Um dies zu spüren, ist es hilfreich, eine kleinere Version dieser Aufgabe in Betracht zu ziehen.

Angenommen, Sie möchten alle irrationalen Zahlen in einem Segment von 0 bis 1 approximieren. Stellen Sie sich vor, alle natürlichen Zahlen von 1 bis 10 sind als Nenner verfügbar. Die Liste der möglichen Brüche ist ziemlich groß. Zuerst 1/1, dann 1/2 und 2/2, dann 1/3, 2/3 und 3/3 und so weiter bis 9/10 und 10/10. Es gibt jedoch keinen Nutzen daraus.

Zum Beispiel ist 2/10 gleich 1/5 und 5/10 gleich 1/2, 2/4, 3/6 und 4/8. Vor dem Erscheinen der Duffin-Schaffer-Hypothese formulierte der sowjetische Mathematiker Alexander Y. Khinchin eine Hypothese einer in der Breite ähnlichen rationalen Annäherung. Sein Satz berücksichtigte jedoch nicht die Tatsache, dass äquivalente Brüche nur einmal gezählt werden sollten.


Dimitris Cuculopoulos (links) und James Maynard bei der Präsentation seiner Beweise auf einer Konferenz in Italien

"Normalerweise sollte Mathematik für die erste Klasse die Problemlösung nicht beeinflussen", sagte Granville. "Aber in diesem Fall hat sie überraschenderweise beeinflusst."

Daher hat die Duffin-Shaffer-Hypothese einen Begriff, der die Anzahl der eindeutigen Brüche (oder reduzierten Brüche) für jeden Nenner zählt. Dieses Mitglied wird zu Ehren seines Erfinders, des Mathematikers des 18. Jahrhunderts, Leonard Euler, die φ-Funktion von Euler genannt. φ (10) ist 4, weil es zwischen 0 und 1 nur vier reduzierte Brüche mit einem Nenner von 10 gibt: 1/10, 3/10, 7/10 und 9/10.

Der nächste Schritt besteht darin, zu berechnen, wie viele irrationale Zahlen unter Verwendung jeder der angegebenen Brüche angenähert werden können. Dies hängt davon ab, welchen Größenfehler Sie akzeptieren möchten. Die Duffin-Shaffer-Hypothese erlaubt es uns, für jeden Nenner einen Fehler zu wählen. Für Brüche mit einem Nenner von 7 können Sie beispielsweise einen zulässigen Fehler von 0,02 annehmen. Für Nenner 10 können Sie den Fehler 0,01 annehmen.

Nachdem die Nenner und Fehlerbedingungen identifiziert wurden, ist es an der Zeit, die Netzwerke auf irrationale Zahlen zu setzen. Erstellen Sie Ihre Brüche auf einer Zahlenlinie zwischen 0 und 1 und zeichnen Sie Fehler in Form von Netzwerken, die sich von dem Bruch auf jeder Seite erstrecken. Wir können sagen, dass alle irrationalen Zahlen, die in das Netzwerk fallen, für die gegebenen Begriffe „zufriedenstellend angenähert“ werden. Die Frage ist: Wie viele irrationale Zahlen haben Sie gefangen?



In jedem Intervall der Zahlenreihe befindet sich eine unendliche Anzahl irrationaler Zahlen, sodass die genaue Anzahl der abgefangenen irrationalen Zahlen nicht geschrieben werden kann. Stattdessen sprechen Mathematiker über den Anteil der Gesamtzahl der irrationalen Zahlen, die von jeder Fraktion erfasst werden. Sie bewerten diese Anteile anhand eines Konzepts wie dem „Maß“ einer Teilmenge von Zahlen - es ist so etwas wie die Schätzung der Anzahl der gefangenen Fische nach Gewicht und nicht nach Menge.

Die Duffin-Schaffer-Hypothese schlägt vor, alle Maße der Teilmengen irrationaler Zahlen zu addieren, die von jeder der approximierenden Fraktionen erfasst werden. Sie repräsentiert diese Zahl als große arithmetische Summe. Dann macht sie ihre Hauptvorhersage: Wenn diese Summe ins Unendliche geht, dann haben Sie fast alle irrationalen Zahlen angenähert; Wenn es nur den Endwert gibt, unabhängig davon, wie viele Kennzahlen Sie zusammengefasst haben, konnten Sie fast keine irrationale Zahl annähern.

Eine ähnliche Frage, ob die Summe gegen unendlich „divergiert“ oder gegen einen endlichen Wert „konvergiert“, stellt sich in vielen Bereichen der Mathematik. Die Hauptaussage der Duffin-Shaffer-Hypothese lautet: Wenn Sie verstehen wollen, ob Sie fast alle irrationalen Zahlen mit einem bestimmten Satz von Nennern und Fehlern approximieren können, müssen Sie nur eines wissen: Divergiert die unendliche Summe der Maße gegen unendlich oder konvergiert sie? auf den Endwert.

"Letztendlich hängt Ihr Erfolg, unabhängig davon, wie Sie sich entscheiden, die Näherung für jeden Nenner zu bewerten, nur von einer Sache ab: ob die unendliche Sequenz divergiert oder nicht", sagte Waaler.

Entscheidungsfindung

Sie fragen sich vielleicht: Was ist, wenn sich Zahlen, die durch einen Bruch angenähert werden, mit Zahlen überschneiden, die durch einen anderen angenähert werden? Werden wir sie bei der Berechnung der Maßnahmen nicht zweimal berücksichtigen?

Bei einigen Approximationssequenzen spielt die Doppelzählung keine Rolle. Mathematiker haben vor einigen Jahrzehnten bewiesen, dass diese Hypothese für Approximationssequenzen gilt, die aus Primzahlen bestehen. Bei vielen anderen Approximationssequenzen ist die Doppelzählung jedoch ein Problem. Daher konnten sich Mathematiker 80 Jahre lang nicht mit dieser Hypothese auseinandersetzen.

Das Ausmaß, in dem verschiedene Nenner sich überschneidende Mengen irrationaler Zahlen erfassen, spiegelt sich in der Anzahl einfacher Teiler wider, die allen Nennern gemeinsam sind. Betrachten Sie die Zahlen 12 und 35. Die Primteiler von 12 sind 2 und 3. Die Primteiler von 35 sind 5 und 7. Mit anderen Worten, die gemeinsamen Primfaktoren von 12 und 35 nicht - daher gibt es viele irrationale Zahlen, die durch Bruchteile von angenähert werden können Die Nenner 12 und 35 schneiden sich nicht besonders.

Was ist mit den Nennern 12 und 20? In 20 schneiden sich einfache Teiler 2 und 5 mit Teilern 12. Auf die gleiche Weise schneiden sich irrationale Zahlen, die durch Brüche mit einem Nenner von 20 angenähert werden können, mit denen, die durch Brüche mit einem Nenner von 12 angenähert werden können. Die Duffin-Shaffer-Hypothese ist am schwierigsten zu beweisen in solchen Situationen - wenn die Zahlen in der Approximationssequenz viele gemeinsame kleine Primteiler haben und der Schnittpunkt vieler Teilmengen von Zahlen, die jeder der Nenner approximiert, auftritt.

"Wenn viele der Nenner, aus denen Sie auswählen, viele kleine einfache Teiler haben, beginnen sie sich gegenseitig zu stören", sagte Sam Chau aus Oxford.

Der Schlüssel zur Lösung der Hypothese bestand darin, einen Weg zu finden, um die Überlappungen von Teilmengen irrationaler Zahlen, die durch Nenner mit gemeinsamen Primteilern angenähert werden, genau zu berechnen. Seit 80 Jahren hat es niemand geschafft, dies zu tun. Cuculopoulos und Maynard gelang es, eine völlig neue Sichtweise auf das Problem zu finden.


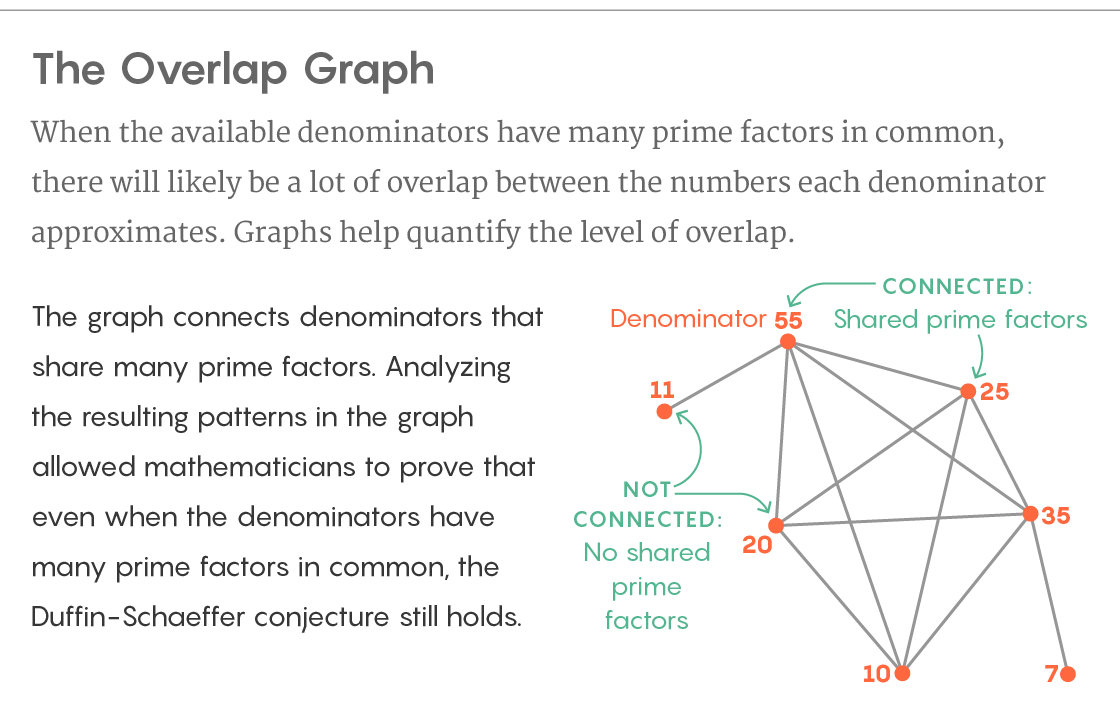Gegenseitige Überlagerungszahl

In ihrem neuen Beweis erstellen sie ein Diagramm aus ihren Nennern. Sie konstruieren sie als Eckpunkte des Graphen und verbinden die Eckpunkte mit einer Kante, wenn sie viele gemeinsame Primteiler haben. Die Struktur des Graphen beschreibt die Überlagerung der Teilmengen irrationaler Zahlen, die jeder der Nenner annähert. Und obwohl diese Überlagerung schwer direkt zu untersuchen ist, haben Kukulopoulos und Maynard einen Weg gefunden, die Struktur des Graphen mit Werkzeugen aus der Graphentheorie zu analysieren - und die benötigten Informationen wurden auf diese Weise gefunden.

"Die Grafik hilft, die Aufgabe visuell zu verstehen. Sie ist eine schöne Sprache, in der Sie über das Problem nachdenken können", sagte Kukulopulos.

Cuculopoulos und Maynard haben bewiesen, dass die Duffin-Shaffer-Hypothese tatsächlich wahr ist: Wenn Sie eine Liste von Nennern mit gültigen Fehlern erhalten, können Sie feststellen, ob es möglich ist, fast alle irrationalen Zahlen zu approximieren, oder Sie können dies nicht einfach tun, indem Sie überprüfen, ob die entsprechende Summe der Maße abweicht zu unendlich oder konvergiert zu einem endlichen Wert.

Dies ist ein eleganter Test, bei dem die allgemeine Frage nach der Art der Approximation durch rationale Zahlen auf einen einzigen berechneten Wert reduziert wird. Nachdem Cuculopoulos und Maynard die Universalität des Testens bewiesen hatten, taten sie eines der größten Dinge für die Mathematik: Sie gaben die endgültige Antwort auf eine grundlegende Frage auf ihrem Gebiet.

"Ihr Beweis ist ein notwendiges und ausreichendes Ergebnis geworden", sagte Green. "Ich nehme an, er markiert das Ende des nächsten Kapitels in Mathematik."