Clustering ist ein wichtiger Bestandteil der Pipeline für maschinelles Lernen zur Lösung wissenschaftlicher und geschäftlicher Probleme. Es hilft, Sätze eng verwandter Punkte (ein bestimmtes Maß für die Entfernung) in der Datenwolke zu identifizieren, die auf andere Weise möglicherweise schwer zu bestimmen sind.

Der Clustering-Prozess bezieht sich jedoch größtenteils auf den Bereich des maschinellen Lernens ohne Lehrer , der durch eine Reihe von Schwierigkeiten gekennzeichnet ist. Es gibt keine Antworten oder Tipps, wie Sie den Prozess optimieren oder den Erfolg des Trainings bewerten können. Dies ist Neuland.

Daher ist es nicht verwunderlich, dass die beliebte Methode des Clustering nach der k-Average-Methode unsere Frage nicht vollständig beantwortet: „Wie ermitteln wir zuerst die Anzahl der Cluster?“ Diese Frage ist äußerst wichtig, da Clustering häufig der weiteren Verarbeitung einzelner Cluster vorausgeht und die Menge der Rechenressourcen von der Bewertung ihrer Anzahl abhängen kann.

Im Bereich der Geschäftsanalyse können sich die schlimmsten Konsequenzen ergeben. Hier wird Clustering für die Marktsegmentierung verwendet, und es ist möglich, dass Marketingmitarbeiter entsprechend der Anzahl der Cluster zugewiesen werden. Eine fehlerhafte Schätzung dieses Betrags kann daher zu einer nicht optimalen Zuweisung wertvoller Ressourcen führen.

Ellbogenmethode

Beim Clustering mit der k-means-Methode wird die Anzahl der Cluster am häufigsten mit der „Elbow-Methode“ geschätzt. Dies impliziert eine mehrfache zyklische Ausführung des Algorithmus mit einer Erhöhung der Anzahl auswählbarer Cluster sowie eine anschließende Verschiebung des Clustering-Scores im Diagramm, berechnet als Funktion der Anzahl der Cluster.

Was ist diese Punktzahl oder Metrik, die im Diagramm verzögert ist? Warum heißt es Ellbogenmethode ?

Ein typisches Diagramm sieht folgendermaßen aus:



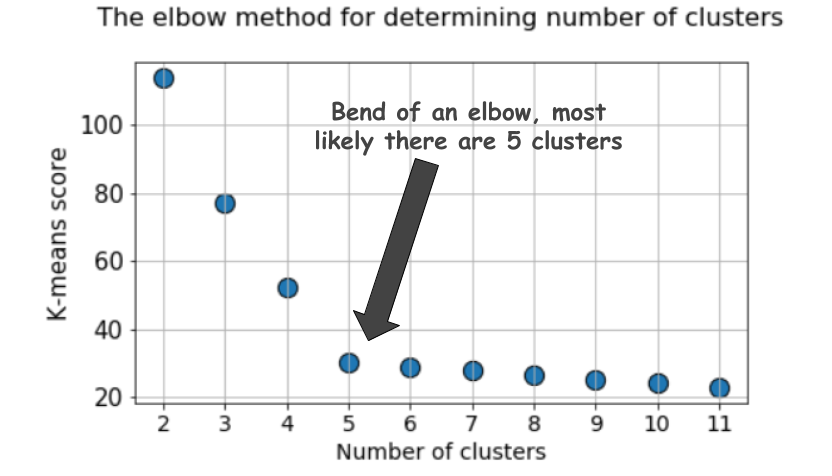
Die Bewertung ist in der Regel ein Maß für die Eingabedaten für die Zielfunktion von k-Mitteln, dh eine Form des Verhältnisses des Intraclusterabstands zum Interclusterabstand.

Diese Bewertungsmethode ist beispielsweise sofort im k-means-Bewertungswerkzeug in Scikit-learn verfügbar.

Aber schauen Sie sich diese Grafik noch einmal an. Es fühlt sich etwas seltsam an. Was ist die optimale Anzahl von Clustern, 4, 5 oder 6?

Es ist nicht klar, oder?

Silhouette ist eine bessere Metrik

Der Silhouette-Koeffizient wird unter Verwendung des durchschnittlichen Intracluster-Abstands (a) und des durchschnittlichen Abstands zum nächsten Cluster (b) für jede Probe berechnet. Die Silhouette wird berechnet als (b - a) / max(a, b) . Lassen Sie mich erklären: b ist der Abstand zwischen a und dem nächsten Cluster, zu dem a nicht gehört. Sie können den durchschnittlichen Silhouettenwert für alle Stichproben berechnen und als Metrik verwenden, um die Anzahl der Cluster zu schätzen.

Hier ist ein Video, das diese Idee erklärt:


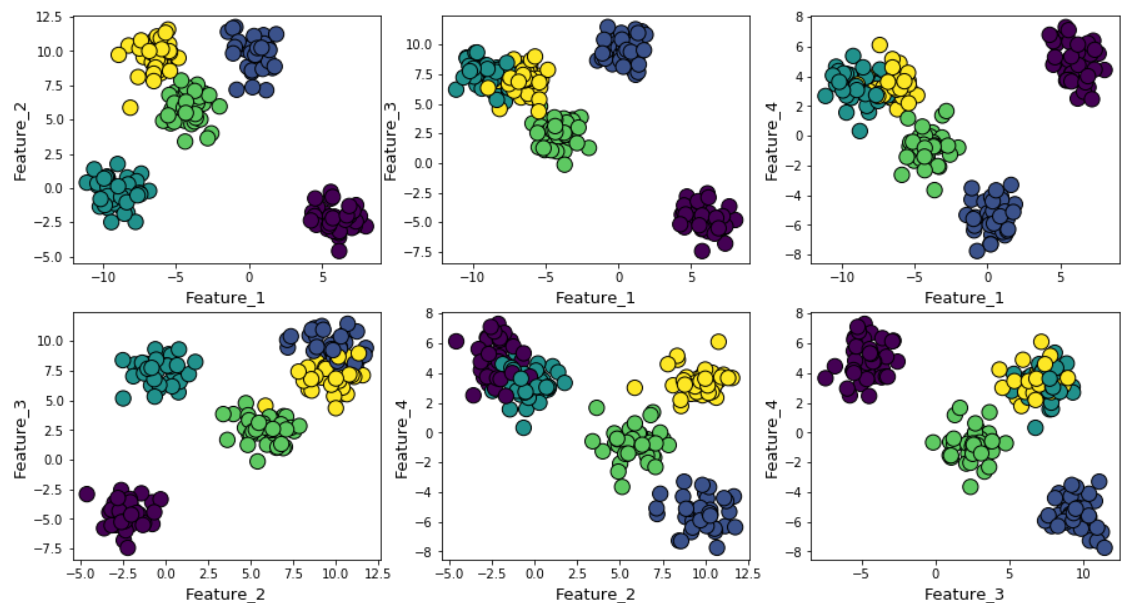
Angenommen, wir haben zufällige Daten mit der Funktion make_blob von Scikit-learn generiert. Die Daten befinden sich in vier Dimensionen und in etwa fünf Clusterzentren. Das Problem besteht im Wesentlichen darin, dass die Daten um fünf Clusterzentren herum generiert werden. Der k-means-Algorithmus weiß dies jedoch nicht.

Cluster können im Diagramm wie folgt angezeigt werden (paarweise Vorzeichen):



Dann führen wir den k-Mittelwert-Algorithmus mit Werten von k = 2 bis k = 12 aus und berechnen dann die Standardmetrik für k-Mittelwert und den durchschnittlichen Silhouettenwert für jeden Lauf, wobei die Ergebnisse in zwei benachbarten Diagrammen angezeigt werden.



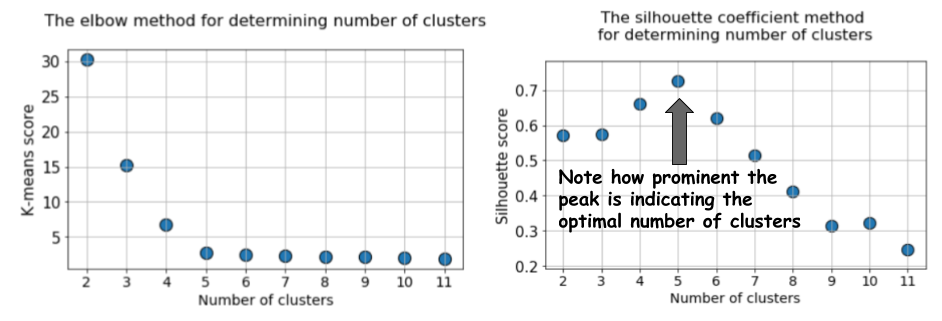
Der Unterschied ist offensichtlich. Der Durchschnittswert der Silhouette steigt auf k = 5 und nimmt dann bei höheren Werten von k stark ab . Das heißt, wir erhalten einen ausgeprägten Peak bei k = 5, dies ist die Anzahl der im ursprünglichen Datensatz generierten Cluster.

Das Silhouettendiagramm hat im Gegensatz zum weich gekrümmten Diagramm bei Verwendung der Ellbogenmethode einen Spitzencharakter. Es ist einfacher zu visualisieren und zu rechtfertigen.

Wenn Sie das Gaußsche Rauschen während der Datengenerierung erhöhen, überlappen sich die Cluster stärker.



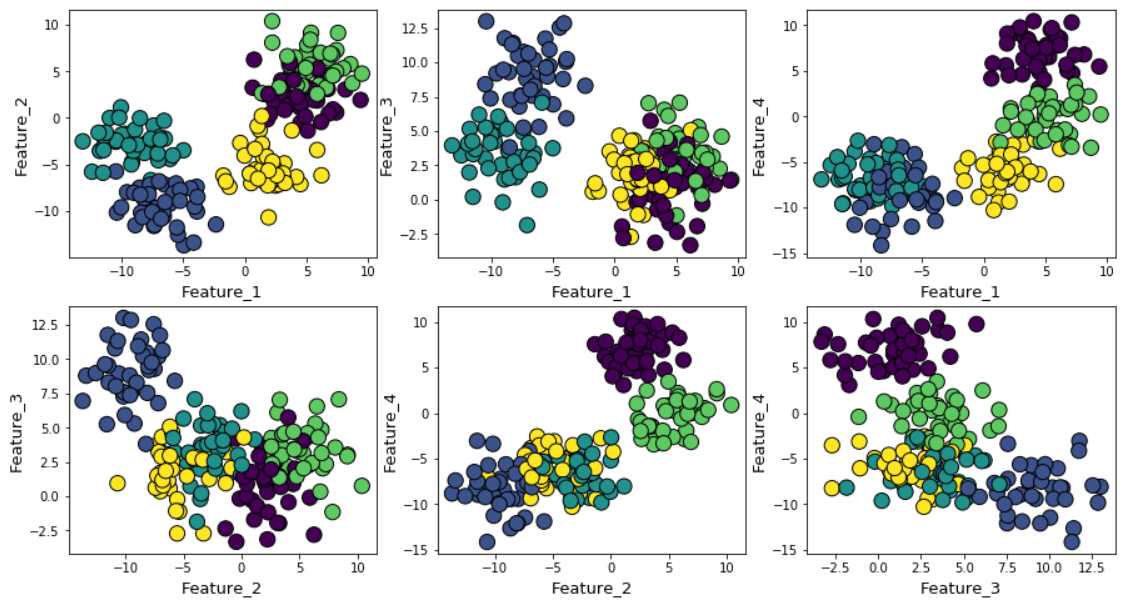
In diesem Fall ergibt die Berechnung des Standard-k-Mittels mit der Ellbogenmethode ein noch ungewisseres Ergebnis. Unten sehen Sie eine grafische Darstellung der Ellbogenmethode, bei der es schwierig ist, einen geeigneten Punkt auszuwählen, an dem sich die Linie tatsächlich biegt. Ist es 4, 5, 6 oder 7?



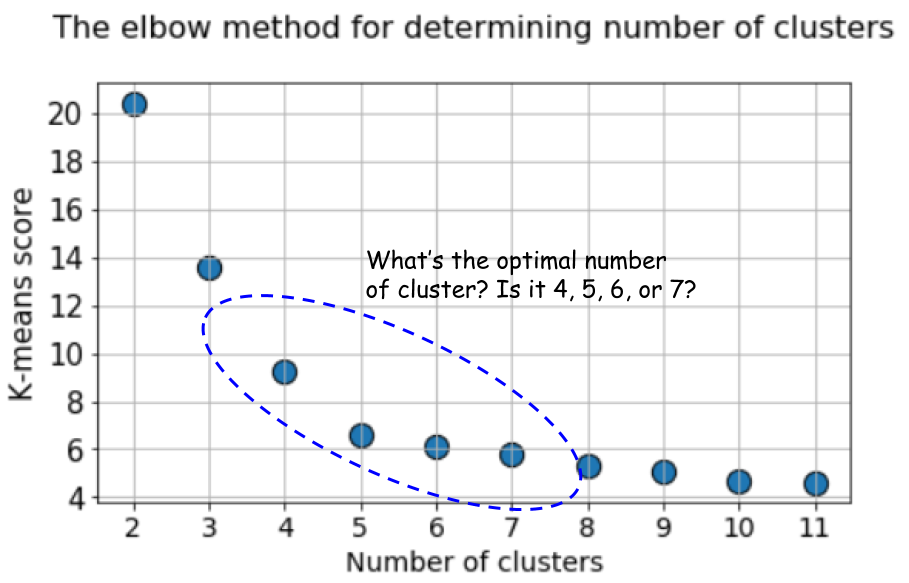
Gleichzeitig zeigt das Silhouette-Diagramm immer noch einen Peak im Bereich von 4 oder 5 Cluster-Zentren, was unser Leben erheblich erleichtert.

Wenn Sie sich überlappende Cluster ansehen, werden Sie feststellen, dass trotz der Tatsache, dass wir Daten um 5 Zentren generiert haben, aufgrund der hohen Streuung nur 4 Cluster strukturell unterschieden werden können. Die Silhouette zeigt dieses Verhalten leicht und zeigt die optimale Anzahl von Clustern zwischen 4 und 5.

BIC-Score mit Normalverteilungsmixmodell

Es gibt andere gute Metriken, um die wahre Anzahl von Clustern zu bestimmen, wie beispielsweise das Bayesian Information Criterion (BIC). Sie können jedoch nur verwendet werden, wenn wir von der k-means-Methode zu einer allgemeineren Version übergehen müssen - einer Mischung aus Normalverteilungen (Gaussian Mixture Model (GMM)).

GMM betrachtet die Datenwolke als Überlagerung zahlreicher Datensätze mit einer Normalverteilung mit separaten Mittelwerten und Varianzen. Und dann verwendet GMM einen Algorithmus, um die Erwartungen zu maximieren und diese Durchschnittswerte und Abweichungen zu bestimmen.

BIC zur Regularisierung

Möglicherweise sind Sie bereits in der statistischen Analyse oder bei Verwendung der linearen Regression auf BIC gestoßen. BIC und AIC (Akaike Information Criterion, Akaike Information Criterion) werden in der linearen Regression als Regularisierungstechniken für den Prozess der Auswahl von Variablen verwendet.

Eine ähnliche Idee gilt für BIC. Theoretisch können extrem komplexe Cluster als Überlagerungen einer großen Anzahl von Datensätzen mit einer Normalverteilung modelliert werden. Um dieses Problem zu lösen, können Sie eine unbegrenzte Anzahl solcher Distributionen anwenden.
Dies ähnelt jedoch der Erhöhung der Komplexität des Modells bei der linearen Regression, wenn eine große Anzahl von Eigenschaften verwendet werden kann, um Daten beliebiger Komplexität abzugleichen, nur um die Möglichkeit einer Verallgemeinerung zu verlieren, da ein übermäßig komplexes Modell dem Rauschen und nicht einem realen Muster entspricht.

Die BIC-Methode verfeinert zahlreiche Normalverteilungen und versucht, das Modell so einfach zu halten, dass ein bestimmtes Muster beschrieben werden kann.

Daher können Sie den GMM-Algorithmus für eine große Anzahl von Cluster-Zentren ausführen, und der BIC-Wert steigt bis zu einem gewissen Punkt an und beginnt dann zu sinken, wenn die Geldstrafe steigt.

Zusammenfassung

Hier ist das Jupyter-Notizbuch für diesen Artikel. Fühlen Sie sich frei zu gabeln und zu experimentieren.

Wir von Jet Infosystems haben einige Alternativen zur beliebten Ellbogenmethode diskutiert, um die richtige Anzahl von Clustern beim Lernen ohne Lehrer mithilfe des k-means-Algorithmus auszuwählen.

Wir haben sichergestellt, dass es besser ist, anstelle der Ellbogenmethode den „Silhouette“ -Koeffizienten und den BIC-Wert (aus der GMM-Erweiterung für k-means) zu verwenden, um die optimale Anzahl von Clustern visuell zu bestimmen.