Hallo!

Hier beschreiben wir die Arbeit eines bestimmten Feldes und machen dann ein paar schöne Features (hier ist alles SEHR einfach).

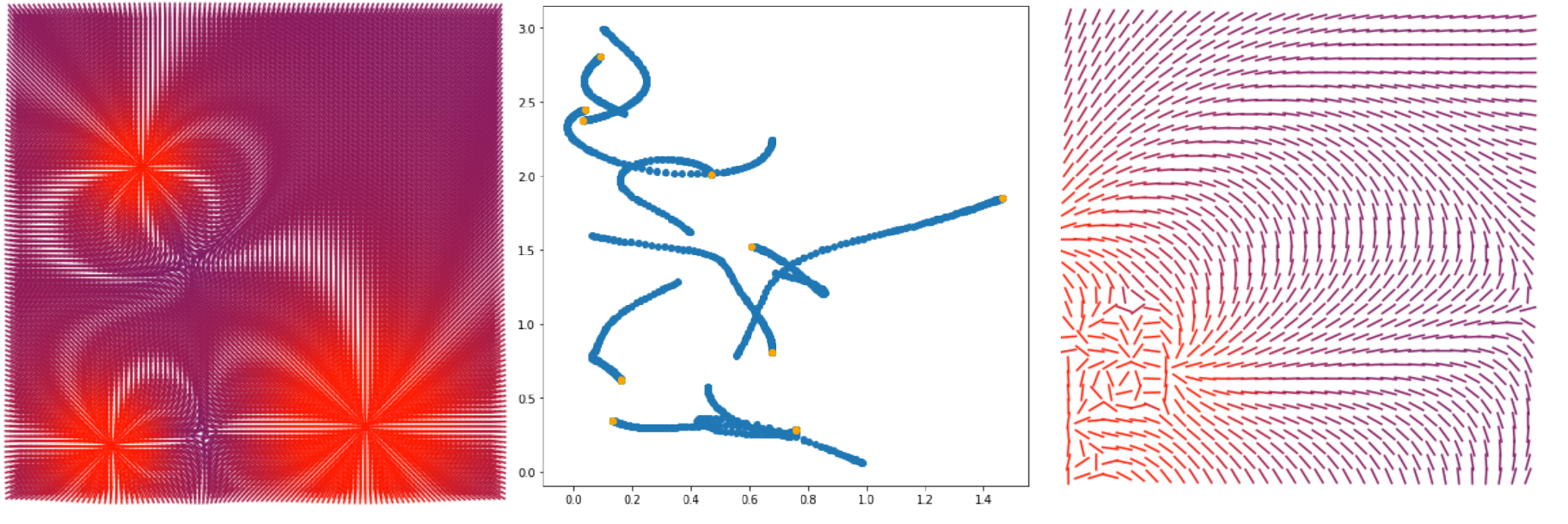
Was wird in diesem Artikel passieren.

Allgemeiner Fall:

Wir beschreiben die Basis, nämlich die Arbeit mit Vektoren (ein Fahrrad für diejenigen, die keine Numpy zur Hand haben)
Wir beschreiben den materiellen Punkt und das Feld der Interaktion

Sonderfall (basierend auf Allgemeinem):

Machen wir eine Visualisierung des Vektorfeldes der elektromagnetischen Feldstärke (erstes und drittes Bild)
Wir werden die Bewegung von Partikeln in einem elektromagnetischen Feld visualisieren

Triff mich unter dem Schnitt!

Theoretische Hintergrundprogrammierung

Vektor

Die Basis aller Fundamente ist ein Vektor (insbesondere in unserem Fall). Daher beginnen wir mit der Beschreibung des Vektors. Was brauchen wir Arithmetische Operationen an einem Vektor, einer Entfernung, einem Modul und einigen technischen Dingen. Der Vektor, den wir von der Liste erben werden. So sieht die Initialisierung aus:

class Vector(list): def __init__(self, *el): for e in el: self.append(e)

Das heißt, jetzt können wir einen Vektor mit erstellen

 v = Vector(1, 2, 3)

Setzen wir die Addition der arithmetischen Operation:

 class Vector(list): ... def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other

Großartig:

 v1 = Vector(1, 2, 3) v2 = Vector(2, 57, 23.2) v1 + v2 >>> [3, 59, 26.2]

In ähnlicher Weise definieren wir alle arithmetischen Operationen (der vollständige Code des Vektors ist niedriger). Jetzt brauchen Sie die Distanzfunktion. Ich könnte einen rustikalen dist (v1, v2) machen - aber das ist nicht schön, also definieren Sie den% -Operator neu:

 class Vector(list): ... def __mod__(self, other): return sum((self - other) ** 2) ** 0.5

Großartig:

 v1 = Vector(1, 2, 3) v2 = Vector(2, 57, 23.2) v1 % v2 >>> 58.60068258988115

Wir brauchen auch ein paar Methoden für eine schnellere Vektorerzeugung und eine schöne Ausgabe. Hier gibt es nichts Schwieriges, also hier den gesamten Code der Vector-Klasse:

Alle Vektor-Klassencodes

 class Vector(list): def __init__(self, *el): for e in el: self.append(e) def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other def __sub__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] - other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self - other def __mul__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] * other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self * other def __truediv__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] / other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self / other def __pow__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] ** other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self ** other def __mod__(self, other): return sum((self - other) ** 2) ** 0.5 def mod(self): return self % Vector.emptyvec(len(self)) def dim(self): return len(self) def __str__(self): if len(self) == 0: return "Empty" r = [str(i) for i in self] return "< " + " ".join(r) + " >" def _ipython_display_(self): print(str(self)) @staticmethod def emptyvec(lens=2, n=0): return Vector(*[n for i in range(lens)]) @staticmethod def randvec(dim): return Vector(*[random.random() for i in range(dim)])

Materialpunkt

Hier ist theoretisch alles einfach - der Punkt hat Koordinaten, Geschwindigkeit und Beschleunigung (der Einfachheit halber). Außerdem hat sie eine Masse und eine Reihe von benutzerdefinierten Parametern (zum Beispiel für ein elektromagnetisches Feld schadet uns eine Ladung nicht, aber niemand stört Sie, auch nur einen Spin einzustellen).

Die Initialisierung erfolgt wie folgt:

 class Point: def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop])

Und um unseren Punkt zu bewegen, zu immobilisieren und zu beschleunigen, werden wir die folgenden Methoden schreiben:

 class Point: ... def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): #        self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0

Gut gemacht, der Punkt selbst ist erledigt.

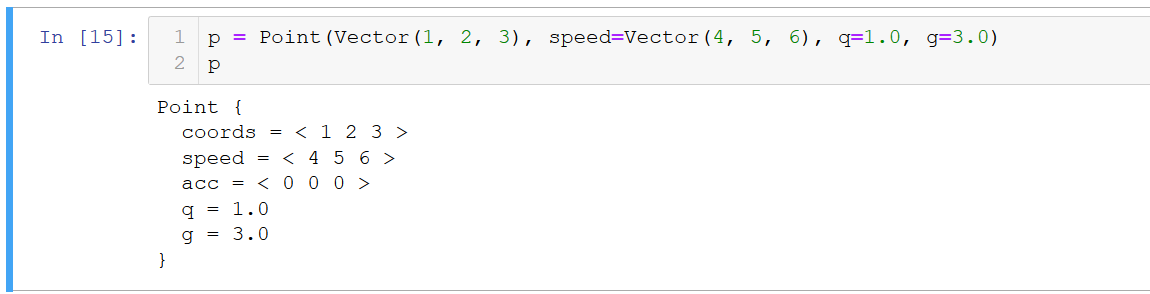
Punktcode (mit schöner Ausgabe)

 class Point: def __init__(self, coords, mass=1.0, q=1.0 speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop]) def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0 def __str__(self): r = ["Point {"] for p in self.__params__: r.append(" " + p + " = " + str(getattr(self, p))) r += ["}"] return "\n".join(r) def _ipython_display_(self): print(str(self))

Ergebnis:

Interaktionsfeld

Wir nennen das Interaktionsfeld ein Objekt, das die Menge aller materiellen Punkte enthält und auf sie Kraft ausübt. Wir werden einen Sonderfall unseres wundervollen Universums betrachten, also werden wir eine benutzerdefinierte Interaktion haben (dies ist natürlich leicht zu erweitern). Deklarieren Sie einen Konstruktor und fügen Sie einen Punkt hinzu:

 class InteractionField: def __init__(self, F): # F -   , F(p1, p2, r), p1, p2 - , r -    self.points = [] self.F = F def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs))

Jetzt macht es Spaß, eine Funktion zu deklarieren, die an diesem Punkt „Spannung“ zurückgibt. Obwohl sich dieses Konzept auf elektromagnetische Wechselwirkungen bezieht, handelt es sich in unserem Fall um einen abstrakten Vektor, entlang dem wir den Punkt verschieben. In diesem Fall haben wir die Eigenschaft des Punktes q, im speziellen Fall die Ladung des Punktes (im Allgemeinen - was auch immer wir wollen, sogar den Vektor). Was ist also Spannung an Punkt C? So etwas wie das:

v e c E (v e c C) = s u m v e c F_{i} (v e c C)

$\ vec E (\ vec C) = \ sum {\ vec F_i (\ vec C)}$

Das heißt, die Spannung am Punkt

v e c C

$\ vec C$ gleich der Summe der Kräfte aller materiellen Punkte, die auf einen Einheitspunkt wirken.

 class InteractionField: ... def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) #       (   ,       F,      ) for p in self.points: if coord % p.coords < 10 ** (-10): #      ,        ,   ,     (  ) continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) #    -  proj = proj + (coord - p.coords) / d * fmod #  return proj

Zu diesem Zeitpunkt können Sie bereits ein Vektorfeld zeichnen, aber wir werden es am Ende tun. Machen wir jetzt einen Schritt in unserer Interaktion

 class InteractionField: ... def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt)

Hier ist alles einfach. Für jeden Punkt bestimmen wir die Spannung in diesen Koordinaten und bestimmen dann die Endkraft auf den ETU-Materialpunkt:

v e c F = v e c E * q

$\ vec F = \ vec E * q$

Definieren Sie die fehlenden Funktionen.

Alle InteractionField-Codes

 class InteractionField: def __init__(self, F): self.points = [] self.F = F def move_all(self, dt): for p in self.points: p.move(dt) def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) for p in self.points: if coord % p.coords < 10 ** (-10): continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) proj = proj + (coord - p.coords) / d * fmod return proj def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt) def clean_acc(self): for p in self.points: p.clean_acc() def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs)) def gather_coords(self): return [p.coords for p in self.points]

Ein Sonderfall. Partikelbewegung und Vektorfeldvisualisierung

Also kamen wir zum interessantesten. Beginnen wir mit ...

Modellierung der Bewegung von Partikeln in einem elektromagnetischen Feld

 u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(3): u.append(Vector.randvec(2) * 10, q=random.random() - 0.5)

Tatsächlich sollte der Koeffizient k gleich einer Art von Milliarden (9 * 10 ^ (- 9)) sein, aber da er zum Zeitpunkt t -> 0 gelöscht wird, habe ich mich sofort entschlossen, beide zu angemessenen Zahlen zu machen. Daher ist in unserer Physik k = 300'000. Und bei allem anderen denke ich, dass es klar ist.

r ** 2 + 0,1

- Dies ist die Vermeidung der Division durch 0. Wir könnten natürlich verwirrt sein, ein großes System von Diffours lösen, aber erstens gibt es keine Bewegungsgleichung für mehr als 2 Körper, und zweitens ist dies eindeutig nicht im Konzept des "Artikels für Anfänger" enthalten.

Als nächstes fügen wir zehn Punkte (zweidimensionaler Raum) mit Koordinaten von 0 bis 10 entlang jeder Achse hinzu. Außerdem geben wir jedem Punkt eine Ladung von -0,25 bis 0,25. Machen Sie nun eine Schleife und zeichnen Sie Punkte entsprechend ihrer Koordinate (und Spuren):

 X, Y = [], [] for i in range(130): u.step(0.0006) xd, yd = zip(*u.gather_coords()) X.extend(xd) Y.extend(yd) plt.figure(figsize=[8, 8]) plt.scatter(X, Y) plt.scatter(*zip(*u.gather_coords()), color="orange") plt.show()

Was hätte passieren sollen:

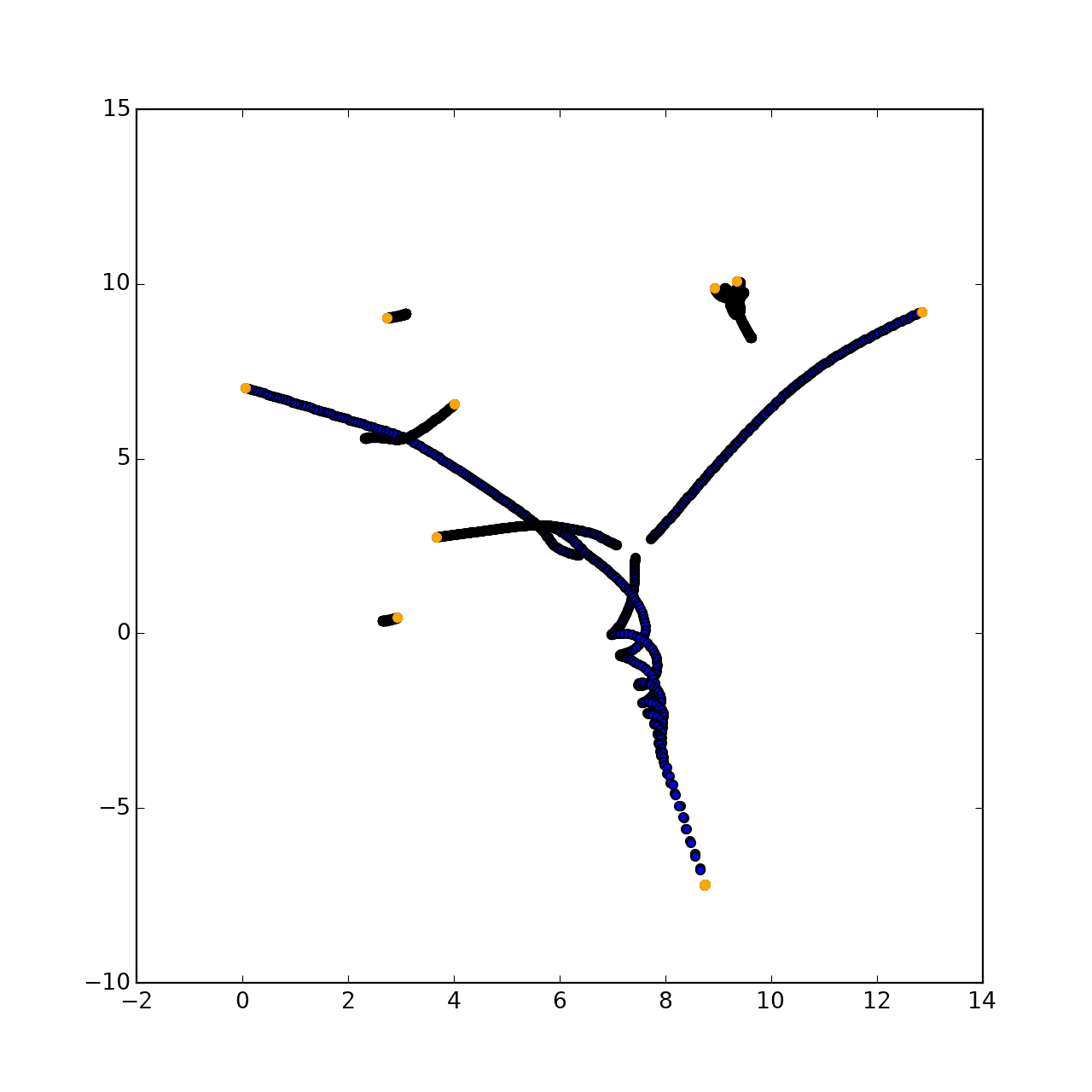
Tatsächlich wird die Zeichnung dort völlig zufällig sein, da die Flugbahn jedes Punktes zum Zeitpunkt der Entwicklung der Mechanik nicht vorhersehbar ist.

Vektorfeldvisualisierung

Hier ist alles einfach. Wir müssen die Koordinaten mit einem Schritt durchgehen und jeweils einen Vektor in die richtige Richtung zeichnen.

 fig = plt.figure(figsize=[5, 5]) res = [] STEP = 0.3 for x in np.arange(0, 10, STEP): for y in np.arange(0, 10, STEP): inten = u.intensity(Vector(x, y)) F = inten.mod() inten /= inten.mod() * 4 #     res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F)) for r in res: plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2])))) #        plt.show()

Ungefähr diese Schlussfolgerung hätte erhalten werden müssen.

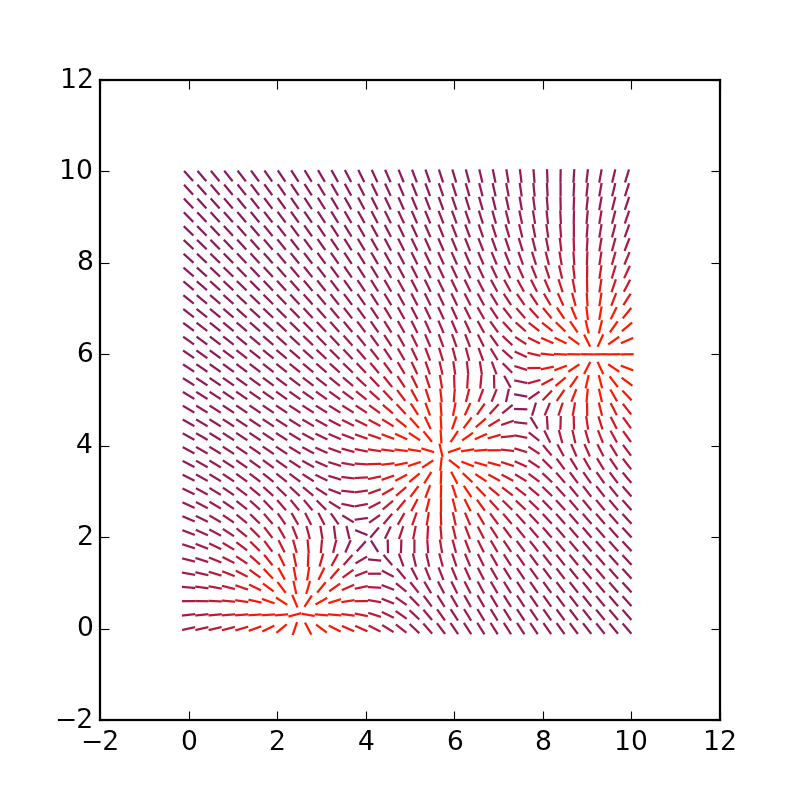
Sie können die Vektoren selbst verlängern und * 4 durch * 1.5 ersetzen:

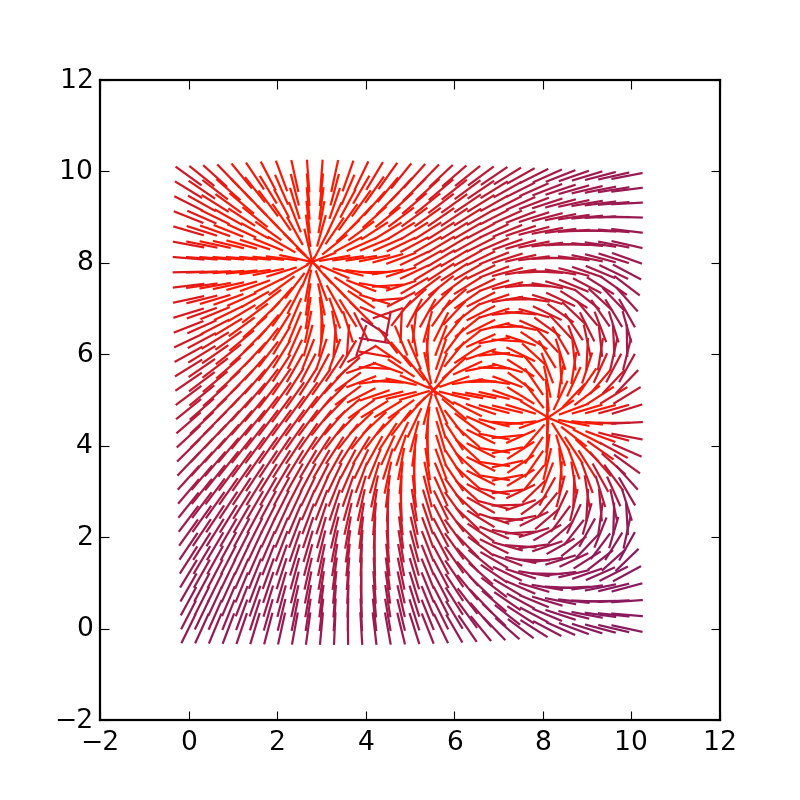
Wir spielen mit Dimensionalität und Modellierung

Erstellen Sie einen fünfdimensionalen Raum mit 200 Punkten und einer Interaktion, die nicht vom Quadrat der Entfernung, sondern vom 4. Grad abhängt.

 u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1)) for i in range(200): u.append(Vector.randvec(5) * 10, q=random.random() - 0.5)

Jetzt sind alle Koordinaten, Geschwindigkeiten usw. in fünf Dimensionen definiert. Lassen Sie uns nun etwas modellieren:

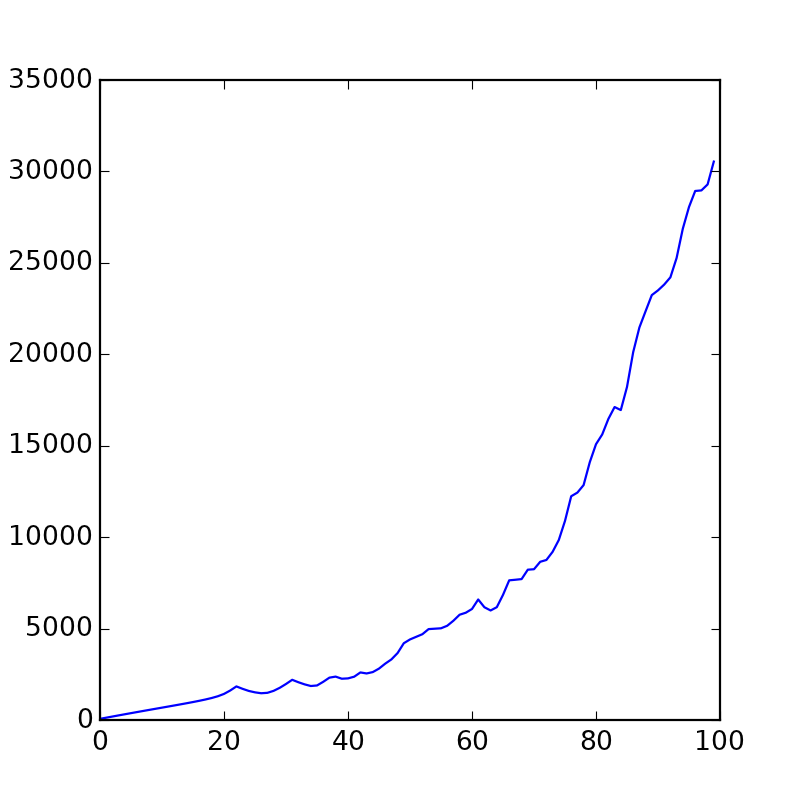
 velmod = 0 velocities = [] for i in range(100): u.step(0.0005) velmod = sum([p.speed.mod() for p in u.points]) #       velocities.append(velmod) plt.plot(velocities) plt.show()

Dies ist ein Diagramm der Summe aller Geschwindigkeiten zu einem bestimmten Zeitpunkt. Wie Sie sehen können, beschleunigen sie sich mit der Zeit langsam.

Nun, das war eine kurze Anleitung, wie man so eine einfache Sache macht. Aber was passiert, wenn Sie mit Blumen spielen:

Alle Code mit Demo

 import random class Vector(list): def __init__(self, *el): for e in el: self.append(e) def __add__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] + other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self + other def __sub__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] - other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self - other def __mul__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] * other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self * other def __truediv__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] / other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self / other def __pow__(self, other): if type(other) is Vector: assert len(self) == len(other), "Error 0" r = Vector() for i in range(len(self)): r.append(self[i] ** other[i]) return r else: other = Vector.emptyvec(lens=len(self), n=other) return self ** other def __mod__(self, other): return sum((self - other) ** 2) ** 0.5 def mod(self): return self % Vector.emptyvec(len(self)) def dim(self): return len(self) def __str__(self): if len(self) == 0: return "Empty" r = [str(i) for i in self] return "< " + " ".join(r) + " >" def _ipython_display_(self): print(str(self)) @staticmethod def emptyvec(lens=2, n=0): return Vector(*[n for i in range(lens)]) @staticmethod def randvec(dim): return Vector(*[random.random() for i in range(dim)]) class Point: def __init__(self, coords, mass=1.0, q=1.0, speed=None, **properties): self.coords = coords if speed is None: self.speed = Vector(*[0 for i in range(len(coords))]) else: self.speed = speed self.acc = Vector(*[0 for i in range(len(coords))]) self.mass = mass self.__params__ = ["coords", "speed", "acc", "q"] + list(properties.keys()) self.q = q for prop in properties: setattr(self, prop, properties[prop]) def move(self, dt): self.coords = self.coords + self.speed * dt def accelerate(self, dt): self.speed = self.speed + self.acc * dt def accinc(self, force): self.acc = self.acc + force / self.mass def clean_acc(self): self.acc = self.acc * 0 def __str__(self): r = ["Point {"] for p in self.__params__: r.append(" " + p + " = " + str(getattr(self, p))) r += ["}"] return "\n".join(r) def _ipython_display_(self): print(str(self)) class InteractionField: def __init__(self, F): self.points = [] self.F = F def move_all(self, dt): for p in self.points: p.move(dt) def intensity(self, coord): proj = Vector(*[0 for i in range(coord.dim())]) single_point = Point(Vector(), mass=1.0, q=1.0) for p in self.points: if coord % p.coords < 10 ** (-10): continue d = p.coords % coord fmod = self.F(single_point, p, d) * (-1) proj = proj + (coord - p.coords) / d * fmod return proj def step(self, dt): self.clean_acc() for p in self.points: p.accinc(self.intensity(p.coords) * pq) p.accelerate(dt) p.move(dt) def clean_acc(self): for p in self.points: p.clean_acc() def append(self, *args, **kwargs): self.points.append(Point(*args, **kwargs)) def gather_coords(self): return [p.coords for p in self.points] #  import matplotlib.pyplot as plt import numpy as np import time #     if False: u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(10): u.append(Vector.randvec(2) * 10, q=(random.random() - 0.5) / 2) X, Y = [], [] for i in range(130): u.step(0.0006) xd, yd = zip(*u.gather_coords()) X.extend(xd) Y.extend(yd) plt.figure(figsize=[8, 8]) plt.scatter(X, Y) plt.scatter(*zip(*u.gather_coords()), color="orange") plt.show() def sigm(x): return 1 / (1 + 1.10 ** (-x/1000)) #    if False: u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 2 + 0.1)) for i in range(3): u.append(Vector.randvec(2) * 10, q=random.random() - 0.5) fig = plt.figure(figsize=[5, 5]) res = [] STEP = 0.3 for x in np.arange(0, 10, STEP): for y in np.arange(0, 10, STEP): inten = u.intensity(Vector(x, y)) F = inten.mod() inten /= inten.mod() * 1.5 res.append(([x - inten[0] / 2, x + inten[0] / 2], [y - inten[1] / 2, y + inten[1] / 2], F)) for r in res: plt.plot(r[0], r[1], color=(sigm(r[2]), 0.1, 0.8 * (1 - sigm(r[2])))) plt.show() #    5-  if False: u = InteractionField(lambda p1, p2, r: 300000 * -p1.q * p2.q / (r ** 4 + 0.1)) for i in range(200): u.append(Vector.randvec(5) * 10, q=random.random() - 0.5) velmod = 0 velocities = [] for i in range(100): u.step(0.0005) velmod = sum([p.speed.mod() for p in u.points]) velocities.append(velmod) plt.plot(velocities) plt.show()

Der nächste Artikel befasst sich wahrscheinlich mit komplexeren Modellen und möglicherweise den Fluiden und Navier-Stokes-Gleichungen.
UPD: Ein Artikel von meinem Kollegen hier

Vielen Dank an MomoDev für die Unterstützung beim Rendern des Videos.

Elementare Simulation der benutzerdefinierten physischen Interaktion in Python + Matplotlib