Und doch, warum Posit eine würdige Alternative zu IEEE 754 sind

Der Monat der Posit auf Habré wurde für offen erklärt, was bedeutet, dass ich die Kritik, die auf sie gefallen ist, nicht übersehen kann. In der vorherigen Serie:

Ein neuer Ansatz kann uns helfen, Gleitkommaberechnungen loszuwerden
Posit-Arithmetik: Besiegt einen Gleitkomma in seinem eigenen Feld. Teil 1
Posit-Arithmetik: Besiegt einen Gleitkomma in seinem eigenen Feld. Teil 2
Erwachsene Posit Herausforderungen

Ich denke, viele von Ihnen können sich sofort an mindestens einen Fall aus der Geschichte erinnern, als revolutionäre Ideen zum Zeitpunkt ihrer Entstehung von einer Expertengemeinschaft abgelehnt wurden. In der Regel ist der Fehler eines solchen Verhaltens das riesige Gepäck an bereits angesammeltem Wissen, das es nicht erlaubt, das alte Problem in einem neuen Licht zu betrachten. Daher verliert die neue Idee an Merkmalen gegenüber etablierten Ansätzen, da sie nur anhand der Metriken bewertet wird, die in der vorherigen Entwicklungsphase als wichtig angesehen wurden.

Dies ist genau die Art von Abneigung, mit der das Posit-Format heute konfrontiert ist: Kritiker schauen oft einfach „in die falsche Richtung“ und verwenden das Posit in ihren Experimenten sogar falsch. In diesem Artikel werde ich versuchen zu erklären warum.

Die Vorteile von Posit wurden bereits mehrfach erwähnt: mathematische Eleganz, hohe Genauigkeit bei niedrigen Exponentialwerten, ein breiter Wertebereich, nur eine binäre Darstellung von NaN und Null, das Fehlen subnormaler Werte, der Kampf gegen Überlauf / Unterlauf. Kritiker wurden vielfach zum Ausdruck gebracht: nutzlose Genauigkeit für sehr große oder sehr kleine Werte, ein komplexes binäres Darstellungsformat und natürlich mangelnde Hardwareunterstützung.

Ich möchte die Argumente, die ich bereits gesagt habe, nicht wiederholen, sondern mich auf den Aspekt konzentrieren, der in der Regel übersehen wird.

Die Spielregeln haben sich geändert

Der IEEE 754-Standard beschreibt Gleitkommazahlen, die vor fast 40 Jahren im Intel 8087 implementiert wurden. Nach den Maßstäben unserer Branche ist dies eine unglaubliche Zeit. Seitdem hat sich alles geändert: Prozessorleistung, Speicherkosten, Datenvolumen und Umfang der Berechnungen. Das Posit-Format wurde nicht nur als beste Version von IEEE 754 entwickelt, sondern auch als Ansatz für die Arbeit mit Zahlen, die den neuen Anforderungen der Zeit entsprechen.

Die übergeordnete Aufgabe ist dieselbe geblieben - wir alle brauchen effektive Berechnungen über den Bereich rationaler Zahlen mit minimalem Genauigkeitsverlust. Die Bedingungen, unter denen die Aufgabe gelöst wird, ändern sich jedoch radikal.

Erstens haben sich die Prioritäten für die Optimierung geändert. Vor 40 Jahren war die Computerleistung fast ausschließlich von der Prozessorleistung abhängig. Heutzutage liegt die Leistung der meisten Computer im Speicher. Um dies zu überprüfen, schauen Sie sich nur die Schlüsselbereiche der Entwicklung von Prozessoren der letzten Jahrzehnte an: dreistufiges Caching, spekulative Ausführung, Pipelining von Berechnungen, Verzweigungsvorhersage. Alle diese Ansätze zielen darauf ab, eine hohe Leistung unter den Bedingungen eines schnellen Rechnens und eines langsamen Zugriffs auf den Speicher zu erzielen.



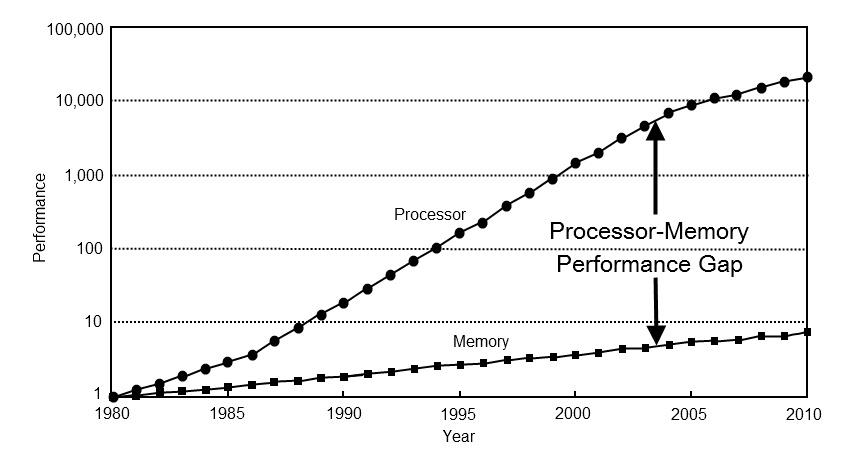
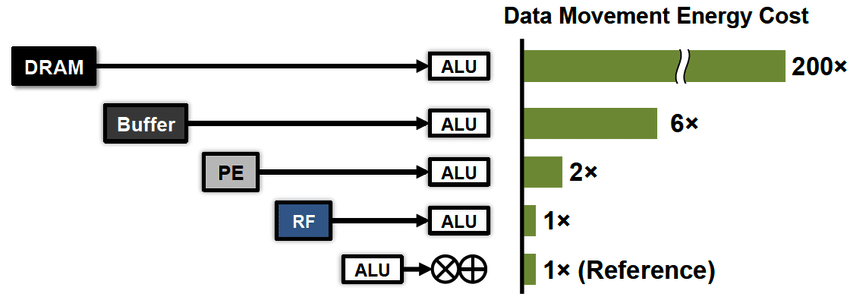
Zweitens ist eine neue Anforderung in den Vordergrund getreten - ein effektiver Energieverbrauch. In den letzten Jahrzehnten hat sich die Technologie der horizontalen Skalierung von Computern so weit entwickelt, dass wir uns nicht mehr so ​​sehr um die Geschwindigkeit dieser Berechnungen, sondern um die Stromrechnung kümmerten. Hier sollte ich einen wichtigen Teil hervorheben, um zu verstehen. Unter dem Gesichtspunkt der Energieeffizienz sind Berechnungen billig, da die Prozessorregister sehr nahe an ihren Computern liegen. Die Bezahlung der Datenübertragung zwischen Prozessor und Speicher (x100) sowie über große Entfernungen (x1000 ...) ist viel teurer.



Hier ist nur ein Beispiel für ein wissenschaftliches Projekt, das Posit verwenden möchte:



Dieses Teleskopnetz erzeugt 200 Petabyte Daten pro Sekunde, deren Verarbeitung die Leistung eines kleinen Kraftwerks in Anspruch nimmt - 10 Megawatt . Offensichtlich ist bei solchen Projekten die Reduzierung des Daten- und Energieverbrauchs von entscheidender Bedeutung.

Bis zum Anfang

Was bietet der Posit-Standard? Um dies zu verstehen, müssen Sie zum Anfang der Diskussion zurückkehren und verstehen, was unter der Genauigkeit von Gleitkommazahlen zu verstehen ist.

Es gibt tatsächlich zwei verschiedene Aspekte in Bezug auf die Genauigkeit. Der erste Aspekt ist die Genauigkeit der Berechnungen - wie stark die Ergebnisse der Berechnungen während verschiedener Operationen abweichen. Der zweite Aspekt ist die Genauigkeit der Darstellung - wie stark der ursprüngliche Wert zum Zeitpunkt der Konvertierung vom Feld der rationalen Zahlen in das Feld der Gleitkommazahlen eines bestimmten Formats verzerrt ist.

Jetzt wird es einen wichtigen Moment für das Bewusstsein geben. Posit ist in erster Linie ein Format zur Darstellung rationaler Zahlen, keine Möglichkeit, Operationen an ihnen durchzuführen. Mit anderen Worten, Posit ist ein verlustbehaftetes rationales Komprimierungsformat. Sie haben vielleicht die Behauptung gehört, dass 32-Bit-Posit eine gute Alternative zu 64-Bit-Float ist. Wir sprechen also davon, die erforderliche Datenmenge zum Speichern und Übertragen des gleichen Satzes von Zahlen genau zu halbieren. Zweimal weniger Speicher - fast zweimal weniger Stromverbrauch und hohe Prozessorleistung aufgrund geringerer Erwartungen an den Speicherzugriff.

Zweites Ende des Stocks

Hier sollten Sie eine logische Frage haben: Was bringt es, rationale Zahlen effizient darzustellen, wenn Berechnungen nicht mit hoher Genauigkeit durchgeführt werden können?

Tatsächlich gibt es eine Möglichkeit, genaue Berechnungen durchzuführen, und diese heißt Quire. Dies ist ein weiteres Format zur Darstellung rationaler Zahlen, die untrennbar mit Posit verbunden sind. Im Gegensatz zu Posit wurde das Quire-Format speziell für Berechnungen und zum Speichern von Zwischenwerten in Registern und nicht im Hauptspeicher entwickelt.



Kurz gesagt, der Quire ist nichts anderes als eine breite Ganzzahlbatterie (Festkomma-Arithmetik). Die Einheit als binäre Darstellung von Quire entspricht dem minimalen positiven Wert von Posit. Der maximale Quire-Wert entspricht dem maximalen Posit-Wert. Jeder Posit-Wert hat eine eindeutige Darstellung in Quire ohne Genauigkeitsverlust, aber nicht jeder Quire-Wert kann in Posit ohne Genauigkeitsverlust dargestellt werden.

Die Vorteile von Quire liegen auf der Hand. Mit ihnen können Sie Operationen mit unvergleichlich höherer Genauigkeit als Float ausführen, und bei Additions- und Multiplikationsoperationen tritt keinerlei Genauigkeitsverlust auf. Der Preis, den Sie dafür zahlen müssen, sind breite Prozessorregister (32-Bit-Posit mit es = 2 entsprechen 512-Bit-Quire), aber dies ist kein ernstes Problem für moderne Prozessoren. Und wenn vor 40 Jahren das Berechnen von über 512-Bit-Ganzzahlen ein inakzeptabler Luxus war, ist es heute eher eine adäquate Alternative zum breiten Zugriff auf Speicher.

Das Puzzle zusammensetzen

Somit bietet Posit nicht nur einen neuen Standard in Form einer Alternative zu Float / Double, sondern auch einen neuen Ansatz für die Arbeit mit Zahlen. Im Gegensatz zu Float - einer einzelnen Darstellung, die versucht, einen Kompromiss zwischen Genauigkeit und Speichereffizienz sowie Recheneffizienz zu finden - bietet Posit zwei verschiedene Präsentationsformate, eines zum Speichern und Übertragen von Zahlen - Posit selbst und das andere für Berechnungen und deren Zwischenprodukte Werte - Quire.

Wenn wir praktische Probleme mit Gleitkommazahlen lösen, kann die Arbeit mit ihnen aus Sicht des Prozessors als eine Reihe der folgenden Aktionen dargestellt werden:

1. Lesen Sie die Werte von Zahlen aus dem Speicher.
2. Führen Sie eine Abfolge von Vorgängen aus. Manchmal ist die Anzahl der Operationen ziemlich groß. In diesem Fall werden alle Zwischenwerte der Berechnungen in Registern gespeichert.
3. Schreiben Sie das Ergebnis von Operationen in den Speicher.

Mit Float / Double geht die Genauigkeit bei jeder Operation verloren. Mit Posit + Quire ist der Genauigkeitsverlust während der Berechnung vernachlässigbar. Es geht erst in der letzten Phase verloren, wenn der Quire-Wert in Posit konvertiert wird. Aus diesem Grund sind die meisten Probleme mit der Fehlerakkumulation für Posit + Quire einfach nicht relevant.

Im Gegensatz zu Float / Double können wir uns bei Verwendung von Posit + Quire normalerweise eine kompaktere Darstellung von Zahlen leisten. Infolgedessen schnellerer Zugriff auf Daten aus dem Speicher (bessere Leistung) und effizientere Speicherung und Übertragung von Informationen.

Mueller Ratio

Zur Veranschaulichung möchte ich nur ein Beispiel nennen - die klassische Müller-Wiederholungsrelation, die speziell geprägt wurde, um zu demonstrieren, wie die Anhäufung von Fehlern bei Gleitkommaberechnungen das Ergebnis von Berechnungen radikal verzerrt.



Bei Verwendung von Arithmetik mit beliebiger Genauigkeit sollte die Wiederholungssequenz auf den Wert 5 reduziert werden. Bei Gleitkomma-Arithmetik stellt sich nur die Frage, bei welcher Iteration die Berechnungsergebnisse eine unzureichend große Abweichung aufweisen.

Ich habe ein Experiment für IEEE 754 mit einfacher und doppelter Genauigkeit sowie für 32-Bit-Posit + Quire durchgeführt. Die Berechnungen wurden in Quire-Arithmetik durchgeführt, aber jeder Wert in der Tabelle wurde in Posit konvertiert.


Wie Sie der Tabelle entnehmen können, gibt 32-Bit-Float bereits den siebten Wert auf, und 64-Bit-Float dauerte bis zur 14. Iteration. Gleichzeitig liefern Berechnungen für Posit mit Quire ein stabiles Ergebnis von bis zu 58 Iterationen!

Moral

In vielen praktischen Fällen und bei korrekter Verwendung können Sie mit dem Posit-Format einerseits Speicherplatz sparen, Zahlen besser komprimieren als Float und andererseits dank Quire eine bessere Berechnungsgenauigkeit erzielen.

Das ist aber nur eine Theorie! Wenn es um Genauigkeit oder Leistung geht, machen Sie immer Tests, bevor Sie blind dem einen oder anderen Ansatz vertrauen. In der Praxis wird sich Ihr spezieller Fall viel häufiger als theoretisch als außergewöhnlich herausstellen.

Vergessen Sie nicht Clarks erstes Gesetz (freie Interpretation): Wenn ein angesehener und erfahrener Experte behauptet, dass eine neue Idee funktionieren wird, hat er mit ziemlicher Sicherheit Recht. Wenn er behauptet, dass die neue Idee nicht funktionieren wird, dann irrt er sich sehr wahrscheinlich. Ich betrachte mich nicht als erfahrenen Experten, damit Sie sich auf meine Meinung verlassen können, aber ich bitte Sie, selbst erfahrene und angesehene Menschen nicht zu kritisieren. Schließlich steckt der Teufel im Detail, und selbst erfahrene Menschen können sie vermissen.