Was steckt hinter der Feigenbaum-Konstante?

Nachruf: Mitchell Feigenbaum, (1944-2019), 4.66920160910299067185320382 ...

Steven Wolfram Blog Artikel



Es wird als Feigenbaum-Konstante bezeichnet und entspricht ungefähr 4.6692016. Und es tritt mit beneidenswerter Periodizität in bestimmten Arten von mathematischen und physikalischen Systemen auf, die chaotisches Verhalten demonstrieren können.

Mitchell Feigenbaum , der uns am 30. Juni im Alter von 74 Jahren verließ, war derjenige, der es entdeckte - 1975, und er tat dies, indem er experimentelle Mathematik auf einem Taschenrechner durchführte.

Diese Entdeckung ist in der Theorie des Chaos entscheidend geworden. Aber als es zum ersten Mal entdeckt wurde, war dieses Ergebnis unerwartet, bizarr und hatte nichts mit dem zu tun, was zuvor untersucht wurde. In gewisser Weise scheint es jedoch angebracht zu sein, dass mich Mitchell Feigenbaum fast 40 Jahre lang entdeckt hat.

Mitchell, der theoretische Physik studierte und ein Kenner seiner mathematischen Traditionen war, schien sich immer als Außenseiter zu betrachten. Er sah Beethoven ein wenig ähnlich - und machte einen eleganten Eindruck von einem bestimmten intellektuellen Geheimnis. Er machte oft starke Aussagen, normalerweise mit einem verschwörerischen Blick, mit einem Schimmer in den Augen und einem Glas Wein oder einer Zigarette in der Hand.

Er sprach in langen, kunstvollen Sätzen, die Gelehrsamkeit und Intellektualität in ihm verrieten. Aber die Ideen daraus gossen am unterschiedlichsten. Manchmal waren sie detailliert und technisch. Manchmal waren dies Intuitionssprünge, die ich zumindest nicht verfolgen konnte. Er las immer etwas, schlief erst 5-6 Stunden, füllte die Gelben Seiten von Notizbüchern mit Formeln und lud das Mathematica-System mit komplexen algebraischen Berechnungen, die Stunden dauern konnten.

Er veröffentlichte wenig und veröffentlichte Werke enttäuschten ihn oft mit der Tatsache, dass nicht viele Menschen sie verstanden. Zum Zeitpunkt seines Todes hatte er viele Jahre an der Optik der Wahrnehmung gearbeitet und an Fragen wie "Warum erscheint der Mond größer, wenn er sich über dem Horizont befindet?". Er beschloss jedoch nicht, so etwas zu veröffentlichen.

Mehr als 30 Jahre lang war Mitchells offizielle Arbeit (die er dank der Eröffnung der Feigenbaum-Konstante erhielt) Professor an der Rockefeller University in New York (um die biologische Forschungsmission des Instituts zu erfüllen, wurde er zum Leiter des "Laboratory of Mathematical Physics" ernannt). Er hat jedoch noch viel Arbeit geleistet, dem Start des Finanzcomputers seinen Namen gegeben und war eng mit der Erfindung neuer kartografischer Methoden für den globalen Atlas Hammond verbunden .

Was Mitchell entdeckt hat

Die Grundidee ist ganz einfach. Nehmen Sie die Zahl x von 0 bis 1. Wir werden x schrittweise durch ax (1 - x) ersetzen. Angenommen, wir beginnen mit x = 1/3 und a = 3,2. Dann sind hier die sequentiellen Werte von x, die wir erhalten:



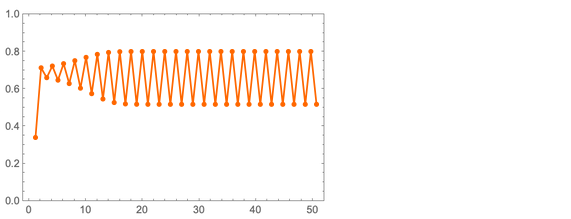
Die Werte von x werden schnell periodisch mit einer Periode von 2. Aber was passiert, wenn wir andere Werte von a nehmen? Hier einige Ergebnisse für die sogenannten "Logistic Mapping":



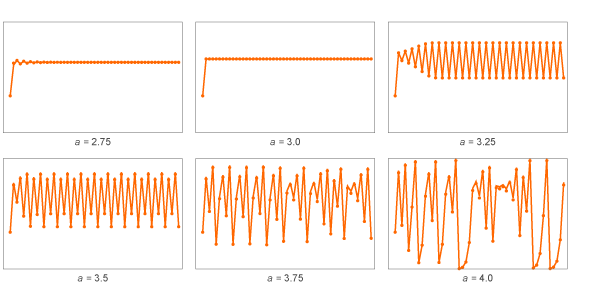
Für kleines a kommen die Werte von x schnell zu festen Werten. Für große a werden sie periodisch, zuerst mit einer Periode von 2, dann 4. Und für größere a beginnen die Werte auf scheinbar zufällige Weise zu springen.

Dies kann zusammengefasst werden, indem die Werte von x (hier sind es 300, nachdem die ersten 50 gelöscht wurden) als Funktion des Werts von a konstruiert werden:



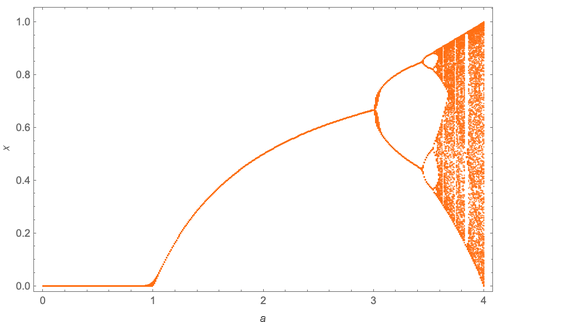
Mit zunehmendem a wird eine Kaskade der Periodenverdopplung beobachtet. In diesem Fall treten sie bei a = 3, a ≤ 3,449, a ≤ 3,544090, a ≤ 3,5644072 auf. Mitchell bemerkte, dass diese aufeinanderfolgenden Werte eine Grenze (a _∞ ≈ 3.569946) in der geometrischen Folge haben, a _∞ - a _n ~ δ ^-n und δ ≈ 4.669.

Ein interessantes Ergebnis. Aber hier ist, was es bedeutet: Dies gilt nicht nur für eine bestimmte iterative Abbildung x → ax (1 - x); Dies gilt für jede Anzeige. Hier ist zum Beispiel das „Bifurkationsdiagramm“ für x → a sin (π √x):



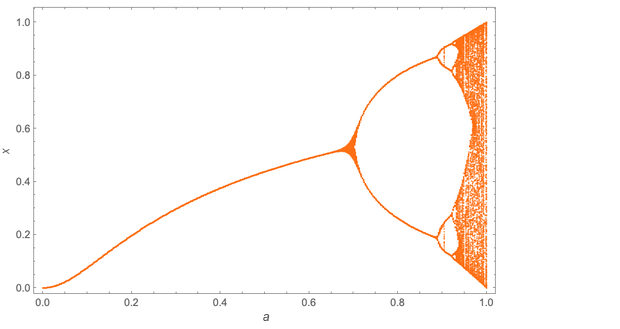
Details unterscheiden sich, aber Mitchell bemerkte, dass die Anordnung der Periodenverdopplung wieder eine geometrische Folge mit genau der gleichen Basis δ ≈ 4.669 bildet.

Und nicht nur diese verschiedenen iterativen Abbildungen ergaben qualitativ ähnliche Ergebnisse. Bei der Messung der Konvergenzrate stellt sich heraus, dass sie genau gleich ist - immer δ ≈ 4.669. Dies war Mitchells große Entdeckung: ein quantitativ universelles Merkmal der Herangehensweise an das Chaos in der Klasse der Systeme.

Wissenschaftlicher Hintergrund

Die Grundidee iterativer Abbildungen hat eine lange Geschichte, die bis in die Antike zurückreicht. Ihre frühen Versionen entstanden im Zusammenhang mit der Suche nach sukzessiven Approximationen, beispielsweise von Quadratwurzeln. Zum Beispiel kann die Newton-Methode aus dem 17. Jahrhundert √2 durch Iterationen x → 1 / x + x / 2 erhalten werden. Ausgehend von x = 1:



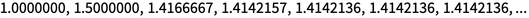
Die Idee einer iterativen Approximation einer beliebigen Funktion wurde offenbar erstmals in der Arbeit von Ernst Schroeder aus dem Jahr 1870 (bekannt für die Formalisierung vieler Dinge, von Graden bis zur Booleschen Algebra) formalisiert, obwohl die meisten Diskussionen die Lösung von Funktionsgleichungen und nicht die Iterationen selbst betrafen (mit Ausnahme der Studie) Konvergenzbereiche der Newtonschen Näherung von Arthur Cayley im Jahr 1879). 1918 führte Gaston Maurice Julia eine umfassende Studie über iterative Materialfunktionen auf der komplexen Ebene durch und erfand das Julia-Set . Doch bevor in den späten 1970er Jahren Fraktale auftauchten (was bald zum Erscheinen des Mandelbrot-Sets führte ), wurde dieser Bereich der Mathematik vegetiert.

Unabhängig von der Forschung in der reinen Mathematik tauchten in den 1930er Jahren iterative Abbildungen mit ähnlichen Formen wie x → ax (1 - x) unter möglichen praktischen Modellen für das Studium der Populationsbiologie oder der Theorie der Konjunkturzyklen auf. Sie erschienen normalerweise in Form diskreter Versionen kontinuierlicher Gleichungen, wie der Verhulst-Logistikgleichung der Mitte des 19. Jahrhunderts. Oszillatorisches Verhalten war ebenfalls häufig - und 1954 fand William Ricoeur (einer der Begründer der wissenschaftlichen Fischerei) auch ein komplexeres Verhalten, wenn er empirische Fischreproduktionskurven durchlief.

In der reinen Mathematik entstanden in der Zahlentheorie periodisch Varianten iterativer Abbildungen. Tatsächlich untersuchte Karl Friedrich Gauß 1799 die Abbildung x → frac (1 / x) im Zusammenhang mit fortgesetzten Fraktionen. Seit dem Ende des 19. Jahrhunderts besteht Interesse an Abbildungen der Form x → frac (ax) und ihrer Beziehung zu den Eigenschaften von a.

Unmittelbar nach der Arbeit von Henri Poincaré an wirksamen Methoden der Himmelsmechanik in den 1900er Jahren tauchte die Idee der Empfindlichkeit gegenüber Anfangsbedingungen auf, und am Ende wurde festgestellt, dass iterative Karten tatsächlich unter Anfangsbedingungen „Zahlen ausgraben“ können. Wenn Sie beispielsweise x → frac (10 x) über π-Ziffern iterieren, wird die Ziffernfolge bei jedem Schritt im Wesentlichen nur um eine Position nach links verschoben:





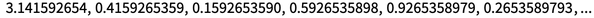
Abbildungen vom Typ x → ax (1-x) zeigen ebenfalls ein ähnliches „Ausgraben von Zahlen“ (wenn beispielsweise x durch sin (π u) ^{2 ersetzt wird} , wird x → 4 x (1-x) genau zu u → frac (u , 2), und dies war bereits in den 1940er Jahren bekannt - zum Beispiel kommentierte John von Neumann dies 1949 im Zusammenhang mit seiner iterativen Mid-Square-Methode zur Erzeugung von Pseudozufallszahlen durch einen Computer.

Was ist jedoch mit experimenteller Mathematik, die auf iterativen Abbildungen basiert? Auf frühen digitalen Computern gab es praktisch keine experimentelle Mathematik (die Computerzeit der meisten von ihnen war zu teuer). Nach dem Manhattan-Projekt in Los Alamos entwickelten sie jedoch einen eigenen MANIAC-Computer, der schließlich für eine Reihe von Studien auf dem Gebiet der experimentellen Mathematik verwendet wurde. 1964 schrieben Paul Stein und Stan Ulam einen Bericht mit dem Titel „Untersuchung nichtlinearer Transformationen auf elektronischen Computern“, der Fotografien von MANIAC-Bildschirmen zeigt, die denen von Oszilloskopen ähneln, und die iterative Darstellungen einer ziemlich komplexen Form zeigen. 1971 lieferte ein weiterer Bericht, der in Los Alamos „aus purer Neugier“ erstellt wurde (verfasst von Nick Metropolis, dem Leiter des MANIAC-Projekts und Entwickler der Monte-Carlo-Methode, sowie Paul Stein und seinem Bruder Miron Stein), spezifischere Rechenergebnisse für logistische Abbildungen und bemerkte das grundlegende Phänomen der Periodenverdopplung (die Autoren nannten es die U-Sequenz) sowie den qualitativen Widerstand gegen Änderungen der zugrunde liegenden Anzeigemethode.

Abgesehen von all dem in Physik und Mathematik gab es andere Entwicklungen. 1964 führte Ed Lorenz (Meteorologe vom MIT) eine Simulation seiner "natürlich vorkommenden" Differentialgleichungen seines Namens ein und erstellte sie, wobei die Empfindlichkeit gegenüber Anfangsbedingungen demonstriert wurde. Seit den 1940er Jahren hat sich ein kontinuierlicher Strom mathematischer Entwicklungen in der Theorie dynamischer Systeme gebildet (die Arbeit basierte auf den Errungenschaften von Poincare aus den 1900er Jahren). Insbesondere untersuchten sie die globalen Eigenschaften von Lösungen von Differentialgleichungen. Normalerweise stießen die Forscher auf Fixpunkte, manchmal auf Grenzzyklen. In den 1970er Jahren, insbesondere nach dem Erscheinen der ersten Computersimulationen (wie bei Lorentz), wurde jedoch klar, dass mit nichtlinearen Gleichungen noch etwas anderes passieren könnte: die sogenannten " seltsamer Attraktor ." Und während des Studierens der "zurückgegebenen Zuordnungen" von seltsamen Attraktoren tauchten wieder iterative Zuordnungen auf.

Es dauerte jedoch bis 1975, bis sich verschiedene Studien iterativer Abbildungen überschnitten. Auf dem Gebiet der reinen Mathematik veröffentlichten der Theoretiker für dynamische Systeme Jim York und sein Student Tien-Yen Lee von der University of Maryland Chaos Follows from Period Three, wo sie zeigten, dass eine iterative Abbildung mit einem bestimmten Parameterwert, dessen Anfangsbedingung zum Auftreten eines Zyklus der Länge drei führt Es muss andere Anfangsbedingungen geben, die nicht zum Auftreten von Zyklen führen - oder, wie sie es beschreiben, Chaos demonstrieren. Dann stellte sich heraus, dass Alexander Sarkovsky, ein Vertreter der sowjetischen Schule für dynamische Systemforschung, bereits 1962 ein etwas schwächeres Ergebnis zeigte, bei dem Zyklen mit allen Perioden aus einem Zyklus mit Periode 3 folgen.

Gleichzeitig begann das Interesse an mathematisch orientierten Spezialisten für Populationsbiologie an logistischen Abbildungen zu wachsen, aus denen die gut geschriebene Übersicht von 1976, Einfache mathematische Modelle mit sehr komplexer Dynamik, hervorging, die von einem australischen Physiker verfasst wurde, der von Robert May , der zu dieser Zeit Professor war, ausgebildet wurde Biologie in Princeton (dann wird er wissenschaftlicher Berater der britischen Regierung und erhält den Titel Baron May of Oxford).

Obwohl es beispielsweise Skizzen von Bifurkationsdiagrammen gab, musste die Entdeckung ihrer universellen numerischen Eigenschaften das Erscheinen von Mitchell Feigenbaum erwarten.

Mitchells Reise

Mitchell Feigenbaum wuchs in Brooklyn, New York, auf. Sein Vater war analytischer Chemiker und seine Mutter unterrichtete an einer öffentlichen Schule. Mitchell studierte nicht besonders gern, obwohl er gute Noten in Prüfungen in Mathematik und den exakten Wissenschaften erhielt und auch selbständig Matalyse lernte und Klavier spielte. 1960, im Alter von 16 Jahren, trat er wie ein Wunderkind in das City College von New York ein, um offiziell Elektrotechnik zu studieren, besuchte aber auch Physik- und Mathematikkurse. Nach seinem Abschluss im Jahr 1964 trat er in das MIT ein. Zunächst wollte er einen Doktortitel in Elektrotechnik verteidigen, wechselte aber schnell zur Physik.

Und obwohl er von der klassischen mathematischen Physik begeistert war (wie sie beispielsweise in den Büchern von Landau und Lifshitz vorgestellt wurde), schrieb er am Ende eine Dissertation zu dem von seinem Kurator festgelegten Thema - Teilchenphysik und eine Bewertung der Klasse der Feynman-Diagramme für die Streuung von Photonen durch skalare Teilchen . Die Dissertation war nicht sehr interessant, aber 1970 wurde er als Postdoc an die Cornell University geschickt.

Mitchell bekam Probleme mit der Motivation und anstatt Physik zu machen, verbrachte er lieber Zeit in Cafés und löste Kreuzworträtsel in der New York Times (was er mit großer Geschwindigkeit schaffte). Aber in Cornell hat Mitchell einige wichtige Freunde gefunden. Einer von ihnen war Predrag Tsvitanovic, ein herausragender Doktorand aus dem Teil Jugoslawiens, der heute Kroatien heißt. Er studierte Quantenelektrodynamik und teilte mit Mitchell ein Interesse an deutscher Literatur. Eine andere war die junge Dichterin Kathleen Durish (die später Katie Hammond wurde), eine Freundin von Predrag. Ein anderer war der aufstrebende Stern der Physik, Professor Pete Carruthers, der mit Mitchell ein Interesse an klassischer Musik teilte.

In den frühen 1970er Jahren näherte sich das goldene Zeitalter der Quantenfeldtheorie. Trotz des Themas seiner Arbeit tat Mitchell dies nicht und brachte nach zwei Jahren in Cornell keine Ergebnisse hervor. Es gelang ihm jedoch, Hans Bethe zu beeindrucken, und er verlegte es an einen anderen Ort, ebenfalls als Postdoc, aber an ein Institut, das einen etwas niedrigeren Platz in der inoffiziellen Hierarchie einnimmt - das Virginia Polytechnic.

Am Virgin Institute hat Mitchell noch weniger getan als in Cornell. Er kommunizierte praktisch nicht mit Menschen und gab nur eine Arbeit auf drei Seiten heraus: „Die Beziehung zwischen dem Normalisierungskoeffizienten und der Dispersionsfunktion in der Transportgleichung von Mehrfachgruppen“. Wie der Name schon sagt, war die Arbeit technisch und uninteressant.

Am Ende von Mitchells zweijährigem Aufenthalt in Virginia war nicht klar, was als nächstes kommen würde. Das Glück griff jedoch ein. Mitchells Freund aus Cornell, Pete Carruthers, wurde beauftragt, eine theoretische Einheit in Los Alamos einzurichten, und erhielt die Erlaubnis, mehrere prominente junge Physiker einzustellen. Pete erzählte mir dann stolz (als Teil des wissenschaftlichen Management-Ratschlags), dass er das Gefühl hatte, dass Mitchell zu etwas Großartigem fähig war, und trotz der Meinungen anderer Leute - und der Beweise - beschloss er, ihn anzuziehen.

Nachdem Pete Mitchell nach Los Alamos versetzt hatte, begann er ihm Projekte anzubieten. Zunächst war es eine Fortsetzung von Petes Arbeit, Versuche, eine Reihe von kollektiven ("Transport") Eigenschaften der Quantenfeldtheorie zu berechnen, um hochenergetische Teilchenkollisionen zu verstehen - dies waren Arbeiten, die Studien über Quark-Gluon-Plasma vorausgingen.

Aber bald schlug Pete vor, dass Mitchell sich insbesondere mit Turbulenzen in Flüssigkeiten befasst, um herauszufinden, ob die Methoden der Renormierungsgruppe in dieser Angelegenheit helfen würden.

Wenn eine Flüssigkeit - zum Beispiel Wasser - schnell genug zu fließen beginnt, erscheinen kleine Strudel darin und sie verhält sich auf komplexe und auf den ersten Blick zufällige Weise. Obwohl dieses Phänomen seit vielen Jahrhunderten qualitativ diskutiert wird (zum Beispiel hat sogar Leonardo da Vinci seine Skizzen angefertigt), konnten Physiker bemerkenswert wenig darüber erzählen - obwohl Andrei Nikolaevich Kolmogorov in den 1940er Jahren die Bemerkung machte, dass Whirlpools mit k eine Kaskade bilden sollten - Energieverteilung. In Los Alamos konzentrierten sich die Wissenschaftler auf die Entwicklung von Atomwaffen (was zwangsläufig die Untersuchung des Verhaltens von Flüssigkeiten mit starken Strömungen beinhaltet), und Turbulenzen waren sehr wichtig zu verstehen - obwohl es nicht offensichtlich war, wie sie angegangen werden sollten.

1974 erschien die Nachricht, dass Kenneth Wilson von Cornell „das Kondo-Problem gelöst hat“ [das Kondo-Problem ist die Unfähigkeit der theoretischen Physik, den Kondo-Effekt zu erklären / ca. trans.] unter Verwendung einer Technik namens "Renormierungsgruppe". Pete Carruthers schlug Mitchell vor, diese Technik auf Turbulenzen anzuwenden.

Die Renormierungsgruppe hängt damit zusammen, wie sich das Ändern der Skala (oder anderer Parameter) auf die Beschreibung (und das Verhalten) der Systeme auswirkt. So kam es, dass Mitchell's PhD vom MIT, Francis Lowe, zusammen mit Murray Gel-Mann es 1954 im Rahmen der Quantenelektrodynamik wieder einführte. Die Idee blieb viele Jahre lang bewegungslos, kam aber in den 1970er Jahren zurück und wurde - wenn auch auf unterschiedliche Weise - sowohl auf die Teilchenphysik (insbesondere die Quantenchromodynamik ) als auch auf die Physik der kondensierten Materie aktiv angewendet.

In einem Stück Eisen im Raum können Sie die Spins aller mit jedem Atom verbundenen Elektronen ausrichten, und dann wird das Eisen magnetisiert. Aber wenn Sie das Eisen aufwärmen, beginnen Schwankungen darin und plötzlich - bei einer Temperatur über dem sogenannten. Curie-Punkte (770 ° C für Eisen) - im Eisen tritt so viel Zufälligkeit auf, dass seine magnetischen Eigenschaften verschwinden. Im Allgemeinen gibt es einige Situationen (Schmelzen, Kochen, Bildung von Verkehrsstaus), wenn dies plötzlich so genannt wird Phasenübergang .

Aber was genau passiert während des Phasenübergangs? Ich denke, der einfachste Weg, dies zu sehen, besteht darin, sein Gegenstück auf dem Gebiet der zellularen Automaten zu untersuchen. Mit einer bestimmten Regel, die unten angegeben ist, wird das System bald weiß, wenn das System anfänglich nicht über eine große Anzahl schwarzer Zellen verfügt. Wenn Sie jedoch die Anzahl der ursprünglichen schwarzen Zellen erhöhen (analog zu einer Erhöhung der Temperatur des Magnetsystems), tritt in diesem Fall bei einem Anteil von 50% der schwarzen Zellen plötzlich ein scharfer Übergang auf, und das gesamte System wird schließlich schwarz (Anmerkung für Experten zu Phasenübergängen: Ja Dies ist ein Phasenübergang in einem eindimensionalen System; ein zweidimensionaler kann nur benötigt werden, wenn das System mikroskopisch reversibel sein muss .



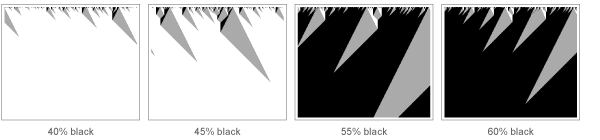
Aber was passiert mit dem System nahe der Grenze von 50% schwarzen Zellen? Tatsächlich kann sie sich nicht entscheiden, ob sie schwarz oder weiß werden soll. Infolgedessen zeigt es eine ganze Hierarchie von Schwankungen, vom kleinsten bis zum größten. In den 1960er Jahren wurde klar, dass die „kritischen Exponenten“, die die Potenzgesetze charakterisieren, die diese Schwankungen beschreiben, für viele Systeme gleich sind.

Aber wie berechnen wir diese kritischen Exponenten? In einigen künstlichen Fällen waren analytische Methoden bekannt. Aber zum größten Teil war etwas anderes erforderlich.In den späten 1960er Jahren erkannte Ken Wilson, dass Renormierungsgruppen und Computer verwendet werden können. Sie können ein Modell für die Interaktion einzelner Drehungen erstellen. Die Renormierungsgruppe bietet Ihnen jedoch ein "Skalierungs" -Verfahren für Interaktionen von immer mehr großen Drehblöcken. Und indem Ken Wilson dies am Computer studierte, gelang es ihm, kritische Exponenten zu berechnen.

, , . . ( ). 1930- , . 1960- , – , .

1975 – . (, , , , , 1980-). , , .

? . - , , - ? .

- . , – – . , , . – – . 1980- , , " 30 " .

? – , , , , . , - ( ). , , , HP-65,

, 1975 , , . , , , , , . , - , a _∞ ≈ 3,56995 π √2. . , .

HP-65, , , , . - , HP-65, a _n .

n . n = 5 30 . n = 6 . , , a _n , , - : , .

Zuerst benutzte er diese Tatsache einfach, um ein _∞ zu schätzen , das er trotz aller Versuche nicht durch Standardkonstanten ausdrücken konnte. Bald jedoch begann er zu vermuten, dass der Konvergenzexponent δ wichtiger war als ein _∞ - da sein Wert bei einfachen Änderungen der Variablen in der Karte unverändert blieb. Mitchell versuchte ungefähr einen Monat lang, δ in Standardkonstanten auszudrücken.

, 1975 , , , , . HP-65 , x → sin(x) , δ .

, . , , . - , - , FORTRAN, – , δ 4,6692.

: CDC 6000 ( , , 1978). , 60- . (14 ) , 4,6692. , , , -, , . δ 11 , , .

Im Laufe mehrerer Wochen entdeckte Mitchell, dass δ ein universeller Wert für alle Iterationskarten mit einem quadratischen Maximum zu sein scheint. Aber er wusste nicht, warum dies geschah, und er hatte keinen spezifischen mathematischen Apparat, um dieses Problem zu untersuchen. Aber am Ende, im Alter von 30 Jahren, entdeckte Mitchell etwas, das ihm wirklich interessant erschien.

An seinem Geburtstag am 19. Dezember traf sich Mitchell mit seinem Freund Predrag und erzählte ihm von diesem Ergebnis. Zu dieser Zeit arbeitete Predrag jedoch mit der Mainstream-Teilchenphysik, und er legte nicht viel Wert darauf.

Mitchell arbeitete weiter und nach einigen Monaten war er überzeugt, dass nicht nur der Exponent δ universell war - mit der richtigen Skala waren die iterativen Abbildungen selbst universell. Im April 1976 schrieb Mitchell einen Bericht über seine Ergebnisse. Am 2. Mai 1976 sprach er in einem Vortrag am Advanced Research Institute in Princeton darüber. Predrag war da und dann interessierte er sich endlich für Mitchells Arbeit.

, . : g(g(x)) = -g(α x)/α, α ≈ 2,50290, , , :

Das Forschungsgebiet der iterativen Abbildungen gewann am 10. Juni 1976 an Dynamik, nachdem Robert May eine Rezension in der Zeitschrift Nature veröffentlicht hatte, die er unabhängig von Mitchell verfasste, und natürlich ohne die erzielten Ergebnisse zu erwähnen. Aber in den folgenden Monaten reiste Mitchell mit seinen Berichten über seine Ergebnisse. Die Reaktion auf sie war gemischt. Die Physiker waren daran interessiert, wie sich diese Ergebnisse auf die Physik auswirken. Mathematiker verstanden ihren Status nicht, da sie aus der experimentellen Mathematik stammten und keinen formalen mathematischen Beweis hatten. Und wie immer war es für die Leute schwierig, Mitchells Erklärungen zu verstehen.

Im Herbst 1976 erhielt Predrag einen Postdoc in Oxford, und am ersten Tag meiner Ankunft traf ich ihn, einen 17-jährigen Studenten, der ein Diplom in Teilchenphysik schrieb. Wir sprachen hauptsächlich über seine elegante „Bird Footprint“ -Methode für die Arbeit mit Gruppentheorie (deren Buch er schließlich 32 Jahre später veröffentlichte). Er versuchte mir auch iterative Karten zu erklären. Und ich erinnere mich noch daran, wie er über ein idealisiertes Modell der Fischpopulation an der Adria sprach (erst nach Jahren verband ich dies mit der Tatsache, dass Predrag von jenen Orten stammte, die heute Kroatien heißen).

Zu dieser Zeit legte ich keinen Wert darauf, aber die Idee der iterativen Zuordnungen verankerte sich in meinem Kopf und vermischte sich bald mit der Idee der Fraktale, die ich aus dem Buch Benoit Mandelbrot gelernt hatte. Und als ich mich nach ein paar Jahren auf die Probleme der Komplexität konzentrierte, halfen mir diese Ideen, zu Systemen wie zellularen Automaten zu gelangen.

Aber 1976 reiste Mitchell (bis zu meinem nächsten Treffen, mit dem noch einige Jahre vergehen werden) aktiv mit Berichten über die Ergebnisse. Er reichte auch Arbeiten bei der renommierten Fachzeitschrift Advances in Mathematics ein. Sechs Monate lang erhielt er keine Nachrichten von dort, aber am Ende wurde die Arbeit abgelehnt. Er versuchte es erneut und schickte einen weiteren Job an das SIAM Journal of Applied Mathematics - mit dem gleichen Ergebnis.

Ich möchte sagen, dass mich das nicht überrascht. Nach meiner Erfahrung mit Veröffentlichungen in der akademischen Literatur (die ich schon sehr lange nicht mehr gemacht habe) ist es recht einfach, eine Arbeit in einem definierten Forschungsbereich zu veröffentlichen. Die Arbeit auf dem Gebiet von etwas wirklich Neuem oder Originellem kann sich jedoch praktisch darauf verlassen, dass es nach einer Expertenbewertung abgelehnt wird - entweder wegen intellektueller Kurzsichtigkeit oder wegen akademischer Korruption. Mitchell hatte ein anderes Problem - seine Erklärungen waren schwer zu verstehen.

Schließlich stimmte Joel Lebovitz, Herausgeber des Journal of Statistical Physics, 1977 der Veröffentlichung von Mitchells Werken zu - tatsächlich, weil er ihn traf, weil er zugab, dass er das Werk nicht verstand. So erschien 1978 die Arbeit „Quantitative Universalität in der Klasse der nichtlinearen Transformationen“, die Mitchells große Leistung beschreibt. Um akademische Prioritäten zu setzen, zitierte Mitchell manchmal eine Zusammenfassung des Berichts, den er am 26. August 1976 erstellt und in der jährlichen Sammlung von Berichten der Los Alamos Theoretical Division für 1975-1976 veröffentlicht hatte. Mitchell war stark von den Verweigerungen beeinflusst, seine Werke zu veröffentlichen, und er bewahrte jahrelang Briefe mit Verweigerungen in einer Schublade auf.

Mitchell reiste weiter um die Welt mit Berichten über die Ergebnisse. Es gab Interesse an ihnen, aber es gab Verwirrung. Im Sommer 1979 geschah jedoch etwas Erstaunliches: Albert Liebhaber aus Paris gab die Ergebnisse eines physikalischen Experiments zum Übergang zu Turbulenzen in konvektiven Strömungen von flüssigem Helium bekannt, bei dem er eine Verdoppelung der Periode genau mit dem von Mitchell berechneten Exponenten δ sah. Es erwies sich nicht nur für die Klasse der mathematischen Systeme als universell, sondern erwies sich auch als in realen physikalischen Systemen.

Und sofort wurde Mitchell berühmt. Eine Verbindung mit der Renormierungsgruppe wurde entdeckt, seine Arbeit wurde sowohl für Physiker als auch für Mathematiker in Mode. Mitchell fuhr weiter mit Berichten, aber jetzt hatte er die Gelegenheit, regelmäßig mit den besten Physikern und Mathematikern abzuhängen.

Ich erinnere mich, wie er irgendwann im Herbst 1979 zu Caltech kam. All dies ähnelte einem Treffen mit einem Rockstar. Mitchell kam, machte einen stilvollen, aber ein wenig mysteriösen Bericht, und dann stahlen ihn Richard Feynman und Murray Gell-Man für ein privates Gespräch.

Bald wurde Mitchell eine Reihe von verschiedenen gehobenen Jobs angeboten, und 1982 kehrte er mit Triumph als Professor für Physik zu Caltech zurück. Es war die Rede davon, dass die Entdeckung einen Nobelpreis verdient, und im Juni 1984 erschien er in der Zeitschrift New York Times mit Beethovens Chic inmitten eines Cornell-Wasserfalls:



Aber die Mathematiker blieben unglücklich. Wie im Fall von Benoit Mandelbrot betrachteten sie Mitchells Ergebnisse als „numerische Hypothesen“, unbewiesen und nicht erwähnenswert. Die besten Mathematiker (mit denen Mitchell sich angefreundet hatte) begannen jedoch bald, an diesem Problem zu arbeiten, und die Ergebnisse ließen nicht lange auf sich warten - obwohl es zehn Jahre dauerte, bis die Universalität von δ vollständig und endgültig bewiesen war.

Wohin ging die Wissenschaft?

Was ist mit Mitchells größter Entdeckung passiert? Es wurde natürlich berühmt. Und Kaskaden mit einer Verdoppelung der Periode mit ihren universellen Eigenschaften wurden bald in einer Reihe von Systemen gefunden - in Flüssigkeiten, Optiken usw. Aber wie häufig waren sie? Könnten sie erweitert werden, um das gesamte Problem der Turbulenzen in einer Flüssigkeit abzudecken?

Mitchell und andere untersuchten andere Systeme als iterative Abbildungen und fanden verwandte Phänomene. Aber unter ihnen waren nicht so überraschend wie Mitchells erste Entdeckung.

In gewisser Weise zielten meine 1981 begonnenen Versuche, zellulare Automaten und das Verhalten einfacher Programme zu untersuchen, darauf ab, nach einigen der großen Fragen zu suchen, zu denen Mitchells Arbeit führen könnte. Unsere Methoden und Ergebnisse waren jedoch sehr unterschiedlich. Mitchell hat immer versucht, solchen Dingen nahe zu bleiben, an die sich traditionelle mathematische Physiker wenden können, und ich bin furchtlos in das Computeruniversum gegangen und habe die dort auftretenden Phänomene untersucht.

Ich habe versucht zu verstehen, wie Mitchells Arbeit mit meiner zusammenhängen könnte, und in meiner ersten Arbeit über zelluläre Automaten im Jahr 1981 habe ich sogar festgestellt, dass die durchschnittliche Dichte schwarzer Zellen in aufeinanderfolgenden Schritten in der Entwicklung eines zellularen Automaten ungefähr durch iterative Kartierung geschätzt werden kann.

Ich habe auch festgestellt, dass mathematisch gesehen die gesamte Entwicklung eines zellularen Automaten als iterative Karte betrachtet werden kann - allerdings nicht auf einer Menge gewöhnlicher reeller Zahlen, sondern auf einer Menge von Kantoren . In meiner ersten Arbeit habe ich sogar ein Analogon von glatten Mitchell-Mappings erstellt, die jedoch wild und zeitweise in mir waren:



Aber egal wie ich es versuchte, ich konnte keine offensichtlichen Zusammenhänge mit Mitchells Arbeit finden. Ich suchte nach Analoga der Verdoppelung der Periode oder Sharkovskys Ordnung , fand aber nichts Besonderes. Für meine Computerplattform war es unnatürlich, an reelle Zahlen mit ihren unendlichen Zahlenfolgen zu denken. Viele Jahre später habe ich in das Buch „Eine neue Art von Wissenschaft“ die Notiz „Smooth Iterative Mapping“ eingefügt. Ich zeigte ihre Zahlenfolge und beobachtete, wie Mitchells Entdeckung das Vorhandensein einer ungewöhnlichen verschachtelten Struktur am Anfang der Folgen impliziert:

Ende der Geschichte

Was ist mit Mitchell passiert? Nachdem er vier Jahre in Cornell verbracht hatte, zog er an die Rockefeller University in New York und führte die nächsten 30 Jahre ein fast unkonventionelles Leben. Die meiste Zeit verbrachte er in seiner Wohnung in der Upper East Side in Manhattan.

In Los Alamos heiratete Mitchell eine Frau deutscher Abstammung namens Cornelia, die Schwester des Physikers (und meines langjährigen Freundes) David Campbell, der das Zentrum für nichtlineare Studien in Los Alamos gründete und dann Rektor der Boston University wurde. Cornelia verließ Mitchell jedoch ziemlich schnell und niemand anderem als Pete Carruthers. Später kam Pete, der unter Alkoholismus und anderen Problemen litt, mit seiner Frau Lucy wieder zusammen, starb jedoch 1997 im Alter von 61 Jahren.

In Cornell lernte Mitchell Gunilla kennen, die im Alter von 14 Jahren aus der Familie eines Pastors aus einer kleinen Stadt in Nordschweden floh, zunächst Model bei Salvador Dali war und 1966 als Model nach New York kam. Gunilla war Journalistin, hat auf Video aufgenommen, Theaterstücke geschrieben und Bilder gemalt. Sie heirateten Mitchell 1986 und ihre Ehe dauerte 26 Jahre, in denen Gunilla eine gute Karriere in der figurativen Kunst machte .

Das neueste Werk, das Mitchell selbst geschrieben hat, wurde 1987 veröffentlicht. Er veröffentlichte auch viele Werke mit verschiedenen Co-Autoren, obwohl keines von ihnen besonders bemerkenswert wurde. Die meisten von ihnen setzten seine frühen Forschungen fort oder versuchten, die traditionellen Methoden der mathematischen Physik auf verschiedene komplexe Phänomene anzuwenden, die dem Flüssigkeitsfluss ähnlich sind.

Mitchell interagierte gern mit den oberen Ebenen der Wissenschaft. Er erhielt alle möglichen Auszeichnungen und Anerkennungen (mit Ausnahme des Nobelpreises). Aber bis zum Ende betrachtete er sich als Außenseiter - ein Renaissance-Mann, der sich auf Physik konzentrierte, aber nicht an alle Institutionen und Praktiken glaubte.

Seit den frühen 1980er Jahren habe ich ziemlich regelmäßig mit Mitchell in New York und anderswo gesehen. Er nutzte die Mathematica-Plattform täglich, lobte sie und sprach oft über die komplexen Berechnungen, die er damit durchführte. Wie viele mathematische Physiker war Mitchell ein Experte für spezielle Funktionen und sprach oft mit mir über immer mehr exotische Funktionen, die wir seiner Meinung nach dem Produkt hinzufügen sollten.

Mitchell hatte zwei große Hobbys außerhalb des akademischen Bereichs. Mitte der 1980er Jahre war die junge Dichterin, die jetzt Katie Hammond heißt und die Mitchell aus Cornell kannte, Werbeleiterin der New York Times und heiratete einen Mann aus einer Familie, der der Hammond World Atlas Publishing House gehörte. Mitchell tauchte dadurch in eine völlig neue Welt der Kartographie ein.

Ich habe viele Male mit ihm über dieses Thema gesprochen. Er war stolz darauf, herausgefunden zu haben, wie man den Riemann-Mapping-Satz verwendet, um beim Erstellen von Karten spezielle lokale Mappings zu erhalten. Er beschrieb mir einen physikbasierten Algorithmus zum Platzieren von Beschriftungen auf Karten (obwohl ich ihn immer noch nicht vollständig verstand). Er war sehr zufrieden mit der Veröffentlichung der neuen Ausgabe von Hammonds Atlas (den er später "mein Atlas" nannte).

Seit den 1980er Jahren hat sich der Trend, physikalische Ideen auf quantitative Finanzierungen anzuwenden, aktiv entwickelt, und Physiker werden häufig zu Wall Street-Analysten. Und da Finanziers ständig nach einzigartigen Vorteilen suchen, besteht immer Interesse an neuen Methoden. Ich wurde oft mit ähnlichen Fragen kontaktiert - aber nach dem Erfolg von James Gleicks 1987 erschienenem Buch „Chaos“ (über das ich ein langes Interview gab) erschien eine ganze Menge Leute, die wissen wollten, wie „Chaos“ ihnen helfen kann, ihre Finanzen zu verwalten.

Einer von ihnen war jemand Michael Gudkin . Er studierte in den frühen 1960er Jahren am College und gründete eine Rechtsforschungsfirma für Jurastudenten. Einige Jahre später stellte er mehrere Ökonomen ein, die den Nobelpreis gewannen, und gründete möglicherweise den ersten Hedgefonds, der sich mit dem Arbitrage-Handel mit Computern befasste. Gudkin war sein ganzes Leben lang ein Motorrad, er liebte Glücksspiel, Reisen und Backgammon und verdiente viel Geld. In einem der unglücklichen Momente suchte er nach einer neuen Lösung - und entdeckte die Theorie des Chaos und Mitchell Feigenbaum.

Er arbeitete mehrere Jahre für verschiedene Physiker, dann stellte er 1995 ein Team zusammen und gründete die Firma Numerix, um den Einsatz physikalischer Berechnungsmethoden im Bereich zunehmend exotischer Finanzinstrumente zu kommerzialisieren. Mitchell Feigenbaum war das Gesicht der Firma, obwohl mein alter Freund Nigel Goldenfield und seine junge Kollegin Sasha Sokol die ganze harte Arbeit trugen.

Das Unternehmen hatte von Anfang an viel Arbeit in Bezug auf die mathematische Physik, und Mitchell beteiligte sich aktiv daran. Er war ein großer Liebhaber von Itos stochastischem Kalkül, hielt Vorträge darüber und war stolz darauf, eine Methode gefunden zu haben, um die stochastische Integration tausendfach zu beschleunigen. Das Unternehmen hat jedoch tatsächlich Bibliotheken in C ++ für die Integration in Bankensysteme geschrieben. Mitchell wollte so etwas auf lange Sicht nicht tun. Nach mehrjähriger Arbeit nahm seine Tätigkeit im Unternehmen ab.

Ich traf mich 1998 mit Gudkin und dann 14 Jahre später. Kurz zuvor schrieb er eine Autobiografie mit dem Titel „Die falsche Antwort, um schneller zu werden: Eine vertrauliche Geschichte der Schaffung einer Billionen-Handelsmaschine“ und nahm plötzlich Kontakt mit mir auf und lud mich ein, an einem neuen, obskuren Geschäft teilzunehmen. Mitchell sprach immer noch gut über Michael, obwohl ich mich weigerte, als plötzlich das Gespräch ging, dass ich eine neue Firma gründete und deren Direktor wurde.

In all den Jahren habe ich ziemlich oft mit Mitchell gesprochen, obwohl unsere Kontakte im Archiv nicht so gut erhalten waren, wie sie sein könnten, weil er lieber per Sprache als per Post sprach. Er schrieb mir einmal: „Ich korrespondiere nicht gerne per E-Mail. Ich höre immer noch lieber die Stimme und interagiere mit der Person. "

Aber einige Fragmente wurden in meinem Archiv aufbewahrt. Es gibt zum Beispiel eine Korrespondenz über Mitchells 60. Geburtstag im Jahr 2004, die ich nicht bekommen habe, weil sie sich mit dem Geburtstag eines meiner Kinder überschnitten hat. Stattdessen bestellte ich die Herstellung des Feigenbaum-Zvitanovich-Kristalls, einer dreidimensionalen Glasskulptur, die die Einschränkung der Funktion g (z) auf der komplexen Ebene darstellt.

Das Lösen der Funktionsgleichung war etwas schwierig, und die Lasergravur spaltete zuerst ein paar Glasblöcke, aber am Ende wurde dieses Objekt hergestellt und verschickt - und viele Jahre später freute ich mich, es in einem Regal in Mitchells Wohnung zu sehen:



Manchmal tauchen in meinen Archiven Erwähnungen von Mitchell bei anderen Personen auf, normalerweise beim Predrag. 2007 schrieb mir Predrag (mit seinem charakteristischen Sinn für Humor):

Zu anderen Neuigkeiten: Ich habe gerade Mitchell getroffen, er trifft sich mit Odyssey.

Ich meine nicht einen teuren Escortservice, sondern Homers Odyssee. Er begann mit der Berechnung der Position von Sternen als Funktion mit einer Präzession von 26.000 Jahren. Er sagt, Hipparch habe dies alles einmal berechnet, aber die katholische Kirche habe es geschafft, alle Kopien seiner Tafeln zu zerstören. "

Mitchell begründete sein Image als Renaissance-Mann und war immer ernsthaft an der Geschichte interessiert. Als Antwort auf meinen Artikel über Leibniz sagte Mitchell 2013, er sei seit seiner Jugend ein Leibniz-Liebhaber und erklärte:

"Newtons Hagiograph Voltaire hatte keine Ahnung von der Essenz der Monadologie , daher konnte ich nur" die beste aller möglichen Welten "vortäuschen. Es war einmal, als ich dies als mündliches Mittel zur Erklärung der Universalität von 2 ^{n veröffentlichte} .

Das zweite Werk von Leibniz, das mit 19 Jahren veröffentlicht wurde, "On Tangent Inversion Methods" oder ähnliches, enthielt die Erfindung der Isokline-Methode zur Lösung gewöhnlicher Differentialgleichungen. Leibniz und Newton beginnen mit Differentialgleichungen, nachdem sie bereits die Differentialnotation erhalten haben. Eine sehr interessante Geschichte. "

Die mathematische Physik war jedoch immer eine Hochburg von Mitchells intellektuellem Leben, wenn auch eher auf persönlicher Ebene als im Rahmen seiner akademischen Arbeit. Irgendwann fragte ihn seine sehr junge Patentochter, warum der Mond, der näher am Horizont sei, größer zu sein scheint. Er schrieb ihr eine Antwort (ein bisschen wie Eulers Briefe an eine deutsche Prinzessin) und stellte dann fest, dass er sich der Antwort nicht sicher war, und begann langjährige Forschungen in den Bereichen Optik und Bildgebung. Am MIT interessierte er sich für die Arbeit der Netzhaut, inspiriert von Jerry Lettwins Buch "Was das Froschauge dem Froschhirn sagt".

Er erzählte mir davon und sagte, dass die übliche Theorie der Bilderzeugung falsch sei und dass er eine bessere Theorie habe. Er hat immer die Größe des Mondes als Beispiel verwendet, aber ich war mir nicht sicher, ob dieses Problem mit der Optik oder der Wahrnehmung zusammenhängt. Er hat nie Werke zu diesem Thema veröffentlicht, obwohl seine Manuskripte (mit Gerüchten, er hat ein Buch vorbereitet) mit etwas Glück das Licht der Welt erblicken werden - wenn jemand anderes sie verstehen kann.

Als ich Mitchell und Gunilla besuchte, machten ihre Wohnungen einen unkonventionellen Eindruck - überall gab es Bücher, Papiere, Gemälde und verschiedene ähnliche Dinge. Und da war ein Vogel. Es war ein Kakadu und es war laut. Ich weiß nicht, wer und warum es gebracht hat. Aber er war ziemlich mühsam. Mitchell und Gunilla wurden aufgrund der Beschwerden der Nachbarn über den Lärm fast aus der Wohnung geworfen und fuhren den Vogel schließlich zu den Ärzten. Wie ich später herausfand, sind Kakadu unerwartet, wenn ich unerwartet den nie umgesetzten Plan zur Entwicklung von Videospielen für Haustiere überprüfe ("die Gedanken eines anderen auf unserem Planeten"), und solche Haustiere brauchen definitiv ein "Twitter für Kakadu".



Infolgedessen verließ Gunilla die Familie, und Gerüchten zufolge lag es am Vogel.

Das letzte Mal, dass wir uns vor einigen Jahren persönlich mit Mitchell getroffen haben. Mein Sohn Christopher und ich besuchten ihn - und er war wie Mitchell aufgeregt, seine Augen funkelten, er sprach schnell und ein wenig mysteriös über das Thema der mathematischen Physik der Bilderzeugung. "Die Augen der Vögel sind überbewertet", sagte er zu dem Geräusch seines Kakadus aus dem Nebenzimmer. Ihre zentrale Fossa ist sehr klein. Ihre Augen arbeiten wie Teleskope. “

« , — , , – . – , », — . , -.

, . , , , . , , . « », , 20 , « -»:



– , . , , . .

, , : 4.66920160910299067185320382…