🦊 👂🏽 🚳 Kosmologie und Quantenfluktuationen im Browser 🏴󠁧󠁢󠁷󠁬󠁳󠁿 🕗 🧒🏾

Setzen wir uns ein rein praktisches Ziel - eine endlose Leinwand mit der Fähigkeit zu realisieren, sie mit der Maus zu bewegen und zu skalieren. Eine solche Zeichenfläche kann beispielsweise als bewegliches Koordinatensystem in einem grafischen Editor dienen. Die Umsetzung unserer Idee ist nicht so kompliziert, aber der Prozess des Verstehens ist mit grundlegenden mathematischen und physikalischen Objekten verbunden, die wir bei unserer Entwicklung berücksichtigen werden.

Ergebnis

Erklärung des Problems

Auf unserer Leinwand möchten wir nur zwei Funktionen ausführen: Bewegen der Maus und Bewegen der Maus sowie Zoomen beim Scrollen. Die Arena unserer Transformationen wird einen Browser auswählen. Waffen müssen in diesem Fall nicht wählen.

Zustandsmaschine

Das Verhalten solcher Systeme wird zweckmäßigerweise durch Übergänge zwischen ihren Zuständen beschrieben, d.h. Zustandsmaschine $\ delta: S \ rightarrow S$ wo $\ delta$ - die Übergangsfunktion zwischen Zuständen, die viele Zustände an sich anzeigt.

In unserem Fall sieht das Zustandsdiagramm folgendermaßen aus:

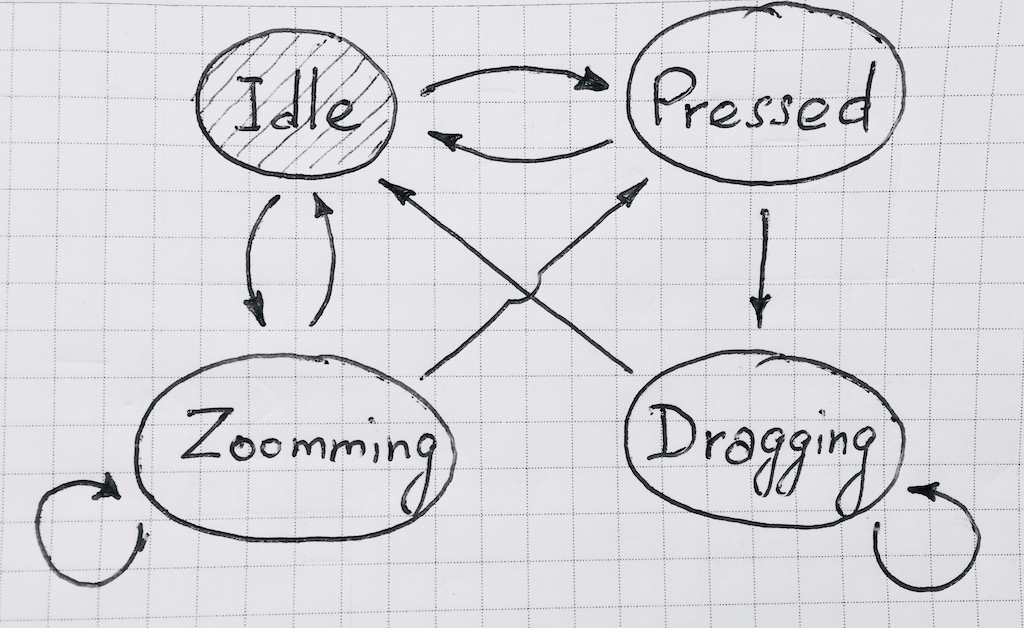
Bei der Implementierung der Übergangsfunktion ist es zweckmäßig, das Ereignis abhängig zu machen. Dies wird sich in Zukunft zeigen. Ebenso ist es bequem, eine Änderung des Zustands der Maschine abonnieren zu können.

type State = string | number; type Transition<States = State> = { to: States, where: (event: Event) => Array<boolean>, }; type Scheme<States = State> = { [key: States]: Array<Transition<States>> }; interface FSM<States = State> { constructor(state: States, scheme: Scheme<States>): void; // Returns true if the scheme had a transition, false otherwise get isActive(): boolean; // Dispatch event and try to do transition dispatch(event: Event): void; // subscribe on state change on(state: States, cb: (event: Event) => any): FSM<States>; // remove subscriber removeListener(state: States, cb: (event: Event) => any): void; };

Wir werden die Implementierung für eine Weile verschieben und die geometrischen Transformationen aufgreifen, die unserer Aufgabe zugrunde liegen.

Geometrien

Wenn das Problem beim Verschieben der Leinwand so offensichtlich ist, dass wir uns nicht damit befassen, sollte das Dehnen genauer betrachtet werden. Zunächst benötigen wir, dass die Dehnung einen einzelnen Punkt stationär lässt - den Mauszeiger. Die Reversibilitätsbedingung muss ebenfalls erfüllt sein, d.h. Die umgekehrte Reihenfolge der Benutzeraktionen sollte die Leinwand an ihre ursprüngliche Position bringen. Welche Geometrie ist dafür geeignet? Wir werden eine Gruppe von Punkttransformationen der Ebene in sich selbst betrachten $\ mathbb {R} ^ 2 \ rightarrow \ mathbb {R} ^ 2$ , was im Allgemeinen durch die Einführung neuer Variablen ausgedrückt wird $x ', y'$ definiert als Funktionen der alten:

x^{'} = v a r p h i (x, y) y^{'} = p s i (x, y)

$x '= \ varphi (x, y) \\ y' = \ psi (x, y)$

In Übereinstimmung mit dem Prinzip der Dualität in der Mathematik können solche Transformationen als Änderung des Koordinatensystems sowie als Transformation des Raums selbst interpretiert werden, wobei letzteres festgelegt ist. Die zweite Interpretation ist für unsere Zwecke zweckmäßig.

Ein modernes Verständnis der Geometrie unterscheidet sich von einem Verständnis der Alten. Nach F. Klein untersucht die Geometrie Invarianten in Bezug auf bestimmte Transformationsgruppen. Also in einer Gruppe von Bewegungen $D$ Die Invariante ist der Abstand zwischen zwei Punkten $d ((x_ {1}, y_ {1}), ((x_ {2}, y_ {2})) = \ sqrt {(x_ {1} - x_ {2}) ^ 2+ (y_ {1 } - y_ {2}) ^ 2}$ . Es enthält parallele Silbentrennung $T _ {(x, y)}$ auf Vektor $(x, y)$ Rotation $R _ {\ phi}$ relativ zum Ursprung in einem Winkel $\ phi$ und Reflexionen $M_ {l}$ relativ zu einer Linie $l$ . Solche Bewegungen nennt man elementar. Die Zusammensetzung der beiden Sätze gehört zu unserer Gruppe und ist manchmal elementar. So zum Beispiel zwei aufeinanderfolgende Spiegelreflexionen relativ zu geraden Linien $l$ und $n$ Drehen Sie sich in einem bestimmten Winkel um ein bestimmtes Zentrum (überzeugen Sie sich selbst):

M_{l} c i r c M_{n} = T_{(- a, - b)} c i r c R_{a l p h a} c i r c T_{(a, b)}

$M_ {l} \ circ M_ {n} = T _ {(- a, -b)} \ circ R _ {\ alpha} \ circ T _ {(a, b)}$

Sicher haben Sie schon vermutet, dass eine solche Gruppe von Bewegungen $D$ bildet euklidische Geometrie. Beim Strecken bleibt jedoch nicht der Abstand zwischen zwei Punkten erhalten, sondern deren Beziehung. Daher eine Gruppe von Bewegungen, obwohl es in unser Schema aufgenommen werden sollte, aber nur als Untergruppe.

Die Geometrie, die zu uns passt, basiert auf einer Dehnungsgruppe $P$ zu dem zusätzlich zu den obigen Bewegungen die Homothetik hinzugefügt wird $S_ {k}$ nach Koeffizienten $k$ .

Nun, der letzte. Das umgekehrte Element muss in der Gruppe vorhanden sein. Und deshalb gibt es eine neutrale $e$ (oder Single) das ändert nichts. Zum Beispiel

S_{k} c i r c S_{k}^{- 1} = e

$S_ {k} \ circ S_ {k} ^ {- 1} = e$

bedeutet zuerst einstrecken

k

$k$ mal und dann in

1 / k

$1 / k$ .

Jetzt können wir die Dehnung in gruppentheoretischer Sprache beschreiben, wobei der Mauszeiger fest bleibt:

(x, y) r i g h t a r r o w (x, y) (T_{(- c l i e n t X, - c l i e n t Y)} c i r c S_{k} c i r c T_{(c l i e n t X, c l i e n t Y)})

$(x, y) \ rightarrow (x, y) (T _ {(- clientX, -clientY)} \ circ S_ {k} \ circ T _ {(clientX, clientY)})$

Anmerkung 1

Im allgemeinen Fall sind Umordnungen von Aktionen nicht kommutativ (Sie können zuerst Ihren Mantel und dann Ihr Hemd ausziehen, aber nicht umgekehrt).

f o r a l l (x, y) i n m a t h b b R^{2} n e q 0 R i g h t a r r o w T_{(- x, - y)} c i r c S_{k} c i r c T_{(x, y)}) n e q S_{k} c i r c T_{(- x, - y)} c i r c T_{(x, y)})

$\ forall (x, y) \ in \ mathbb {R} ^ 2 \ neq 0 \ Rightarrow T _ {(- x, -y)} \ circ S_ {k} \ circ T _ {(x, y)}) \ neq S_ {k} \ circ T _ {(- x, -y)} \ circ T _ {(x, y)})$

Drücken Sie die Bewegung aus $T _ {(x, y)}$ und $S_ {k}$ und ihre Zusammensetzung als Funktionen eines Vektors im Code

 type Scalar = number; type Vec = [number, number]; type Action<A = Vec | Scalar> = (z: Vec) => (v: A) => Vec; // Translate const T: Action<Vec> = (z: Vec) => (d: Vec): Vec => [ z[0] + d[0], z[1] + d[1] ]; // Scale const S: Action<Scalar> = (z: Vec) => (k: Scalar): Vec => [ z[0] * k, z[1] * k ]; const compose = (z: Vec) => (...actions: Array<(z: Vec) => Vec>) => actions.reduce((z, g) => g(z), z);

Schmerz 1

Es ist sehr seltsam, dass in JavaScript keine Operatorüberladung auftritt. Es scheint, dass es bei einer derart weit verbreiteten Verwendung von Vektor- und Rastergrafiken viel bequemer ist, mit Vektoren oder komplexen Zahlen in einer "klassischen" Form zu arbeiten. Die Aktionskonzepte würden arithmetische Operationen ersetzen. So zum Beispiel Rotation um einen Vektor $a$ an der Ecke $\ phi$ würde auf triviale Weise ausgedrückt werden:

T_{- a} c i r c R_{p h i} c i r c T_{a} L i n k e r r e c h t e r P f e i l z r e c h t e r P f e i l (z - a) e^{i p h i} + a

$T _ {- a} \ circ R _ {\ phi} \ circ T_ {a} \ Linker rechter Pfeil z \ rechter Pfeil (z-a) e ^ {i \ phi} + a$

Leider folgt JS nicht der Entwicklung der wunderbaren pythagoreischen Idee „Die Welt ist eine Zahl“, im Gegensatz zu zumindest Python.

Beachten Sie, dass wir bisher mit einer Gruppe kontinuierlicher Transformationen gearbeitet haben. Der Computer arbeitet jedoch nicht mit kontinuierlichen Mengen. Daher verstehen wir nach Poincare eine kontinuierliche Gruppe als eine unendliche Gruppe diskreter Operationen. Nachdem wir die Geometrie herausgefunden haben, sollten wir uns der Relativität der Bewegung zuwenden.

Kosmologie der Leinwand. Modulares Raster

Als Menschheit ist seit einem Jahrhundert die Expansion des Universums bekannt. Wenn wir entfernte Objekte - Galaxien und Quasare - beobachten, registrieren wir die Verschiebung des elektromagnetischen Spektrums zu längeren Wellen - die sogenannte kosmologische Rotverschiebung. Jede Messung verbindet den Beobachter, das Beobachtete und die Messmittel, in Bezug auf die wir unsere Messungen durchführen. Ohne Messinstrumente ist es unmöglich, invariante Beziehungen in der Natur herzustellen, d. H. Die Geometrie des Universums zu bestimmen. Die Geometrie verliert jedoch ihre Bedeutung ohne Beobachtbarkeit. In unserer Aufgabe ist es also schön, Orientierungspunkte wie Galaxien zu haben, in Bezug auf deren Licht wir die Relativität der Bewegung unserer Leinwand bestimmen können. Eine solche Struktur kann ein periodisches Gitter sein, das sich jedes Mal teilt, wenn der Raum zweimal erweitert wird.

Da das Gitter periodisch ist, ist es zweckmäßig, eine modulare Algebra anzuwenden. Wir werden also als Gruppe agieren $P$ auch auf dem Torus $T ^ 2 = S ^ 1 \ mal S ^ 1$ . Da der Monitorbildschirm keine durchgehende Ebene ist, sondern ein ganzzahliges Gitter $\ mathbb {Z} ^ 2$ (Wir vernachlässigen jetzt, dass es endlich ist), dann die Aktion der Gruppe $P$ muss auf einem ganzzahligen Torus berücksichtigt werden $\ mathbb {Z} _ {p} ^ 2$ wo $p$ - quadratische Rippengröße $p \ times p$ ::

Wenn wir also unseren Torus ein für alle Mal in der Nähe des Ursprungs fixieren, werden wir alle weiteren Berechnungen daran durchführen. Verbreiten Sie es dann mit Standardmethoden für die Canvas-Bibliothek. So sieht eine Bewegung mit einem Pixel aus:

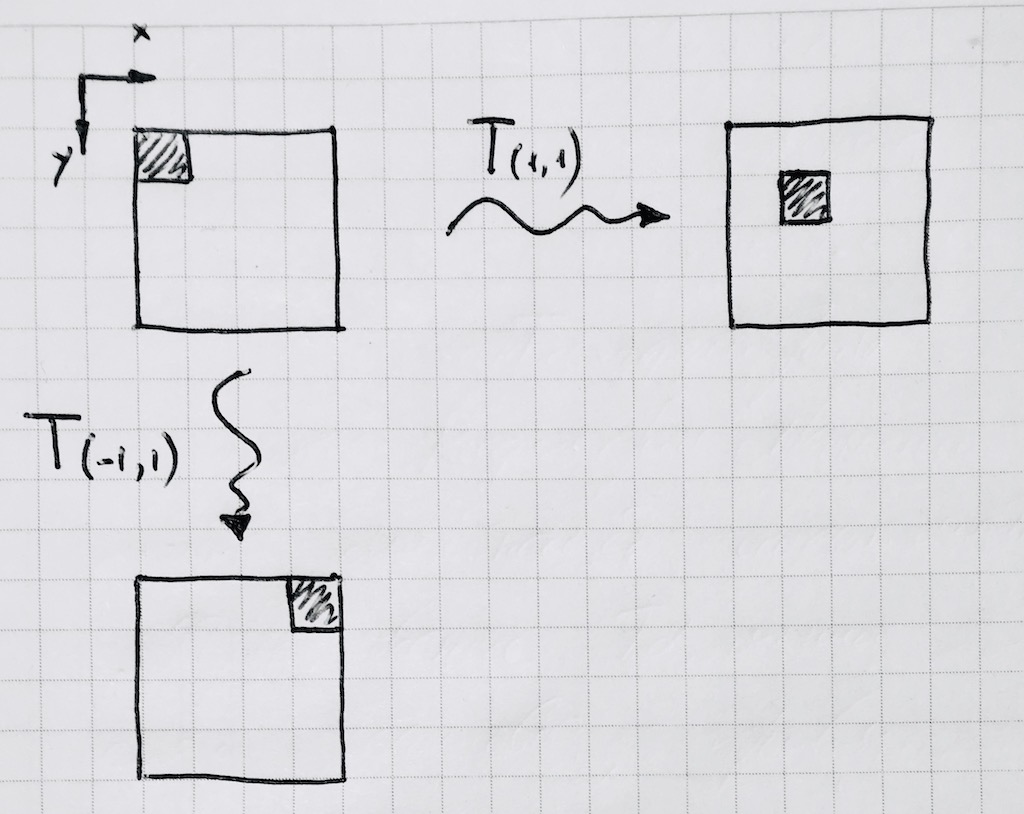
Offensichtlich ist die Standardoperation, das Modul x% p zu nehmen, für uns nicht geeignet, da sie negative Werte des Arguments in negative Werte übersetzt, aber es gibt keine auf dem ganzzahligen Torus. Schreiben Sie Ihre Funktion $x \ mod p$ ::

 const mod = (x, p) => x >= 0 ? Math.round(x) % p : p + Math.round(x) % p;

Nun zurück zur Endzustandsmaschine und

definiere es

Die FSM-Klasse wird bequem von EventEmitter geerbt, wodurch wir die Möglichkeit haben, sie zu abonnieren.

 class FSM<States> extends EventEmitter { static get TRANSITION() { return '__transition__'; } state: States; scheme: Scheme<States>; constructor(state: States, scheme: Scheme<States>) { super(); this.state = state; this.scheme = scheme; this.on(FSM.TRANSITION, event => this.emit(this.state, event)); } get isActive(): boolean { return typeof(this.scheme[this.state]) === 'object'; } dispatch(event: Event) { if (this.isActive) { const transition = this.scheme[this.state].find(({ where }) => where(event).every(domen => domen) ); if (transition) { this.state = transition.to; this.emit(FSM.TRANSITION, event); } } } }

Definieren Sie als Nächstes ein Übergangsschema, erstellen Sie eine Zeichenfläche und

initialisiere alles.

 canvas = document.getElementById('canvas'); ctx = canvas.getContext('2d'); // Create a pattern, offscreen patternCanvas = document.createElement('canvas'); patternContext = patternCanvas.getContext('2d'); type States = | 'idle' | 'pressed' | 'dragging' | 'zooming'; const scheme: Scheme<States> = { 'idle': [ { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'zooming', where: event => [event.type === 'wheel'] }, ], 'pressed': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'moving': [ { to: 'moving', where: event => [event.type === 'mousemove'] }, { to: 'idle', where: event => [event.type === 'mouseup'] }, ], 'zooming': [ { to: 'zooming', where: event => [event.type === 'wheel'] }, { to: 'pressed', where: event => [event.type === 'mousedown'] }, { to: 'idle', where: event => [true] }, ], }; const fsm: FSM<States> = new FSM('idle', scheme); const dispatch = fsm.dispatch.bind(fsm);

Anschließend sollten Sie die Rendering-Funktion festlegen, die erforderlichen Anfangswerte festlegen und die Statusänderung abonnieren. Betrachten Sie den interessantesten Teil des Codes:

  fsm.on('zooming', (event: WheelEvent) => { // next scale factor const nk = g >= 1 ? round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e2) : round(k + Math.sign(event.wheelDeltaY) * h * g / 1e2, 1e12); // gain g = 2 ** Math.trunc(Math.log2(nk)); if (g < min || g > max) return; vec = compose(vec)( T([-event.clientX, -event.clientY]), S(nk / k), T([event.clientX, event.clientY]) ); size = base * nk; patternCanvas.width = Math.round(size / g); patternCanvas.height = Math.round(size / g); xyMod = [ mod(vec[0], patternCanvas.width), mod(vec[1], patternCanvas.height) ]; k = nk; main(); });

Erstens erweitern wir nicht um den Koeffizienten k, sondern um ein Verhältnis nk / k. Dies liegt daran, dass der m-Schritt unserer Abbildung an einem festen Punkt liegt $(a, b)$ ausgedrückt als

x_{m} = (x_{m - 1} - a) k_{m - 1}^{*} + a y_{m} = (y_{m - 1} - b) k_{m - 1}^{*} + b

$x_ {m} = (x_ {m-1} -a) k_ {m-1} ^ * + a \\ y_ {m} = (y_ {m-1} -b) k_ {m-1} ^ * + b$

oder relativ zu den Anfangswerten $x_ {1}, y_ {1}$

x_{m} = (x_{1} - a) p r o d_{i = 1}^{m - 1} k_{i}^{*} + a y_{m} = (y_{1} - b) p r o d_{i = 1}^{m - 1} k_{i}^{*} + b

$x_ {m} = (x_ {1} -a) \ prod_ {i = 1} ^ {m-1} k_ {i} ^ * + a \\ y_ {m} = (y_ {1} -b) \ prod_ {i = 1} ^ {m-1} k_ {i} ^ * + b$

Offensichtlich das Produkt $\ prod_ {i = 1} ^ {m-1} k_ {i} ^ *$ Es gibt eine nichtlineare Funktion des Iterationsschritts, die entweder sehr schnell gegen Null konvergiert oder mit kleinen anfänglichen Abweichungen ins Unendliche abläuft.

Wir führen die Variable g ein, die ein Maß für die Verdoppelung unserer Leinwand ist. Offensichtlich nimmt es in einem bestimmten Intervall einen konstanten Wert an. Linearität erreichen $k_ {i} ^ *$ Wir verwenden eine homogene Substitution

k_{i + 1}^{*} = f r a c k_{i + 1} k_{i}, k_{1} = 1

$k_ {i + 1} ^ * = \ frac {k_ {i + 1}} {k_ {i}}, k_ {1} = 1$

Dann werden alle Mitglieder der Arbeit außer dem ersten und dem letzten reduziert:

p r o d_{i = 1}^{m - 1} k_{i}^{*} = p r o d_{i = 1}^{m - 1} f r a c k_{i} k_{i - 1} = f r a c k_{2} 1 f r a c k_{3} k_{2} . . . f r a c k_{m - 2} k_{m - 3} f r a c k_{m - 1} k_{m - 2} = k_{m - 1}

$\ prod_ {i = 1} ^ {m-1} k_ {i} ^ * = \ prod_ {i = 1} ^ {m-1} \ frac {k_ {i}} {k_ {i-1}} = \ frac {k_ {2}} {1} \ frac {k_ {3}} {k_ {2}} ... \ frac {k_ {m-2}} {k_ {m-3}} \ frac { k_ {m-1}} {k_ {m-2}} = k_ {m-1}$

Ferner reduziert der Phasensprung g die Expansionsrate derart, dass sich die fraktale Struktur, die sich vor uns entfaltet, immer linear bewegt. Somit erhalten wir eine ungefähre Variation des Hubble-Potenzgesetzes der Expansion des Universums.

Es bleibt die Grenzen der Genauigkeit unseres Modells zu verstehen.

Quantenschwankungen. 2-adic Zahlenfeld

Das Verständnis des Messprozesses führte zum Konzept einer reellen Zahl. Heisenbergs Unsicherheitsprinzip weist auf seine Grenzen hin. Ein moderner Computer arbeitet nicht mit reellen Zahlen, sondern mit Maschinenwörtern, deren Länge von der Kapazität des Prozessors bestimmt wird. Maschinenwörter bilden ein Feld von 2-adischen Zahlen $\ mathbb {Q_ {2}}$ und werden als bezeichnet $\ mathbb {F_ {2} ^ {n}}$ wo $n$ - Wortlänge. Der Messprozess wird in diesem Fall durch den Berechnungsprozess ersetzt und ist einer nicht-archimedischen Metrik zugeordnet:

f o r a l l n i n m a t h b b Z, z i n m a t h b b F_{2}^{n} : n c d o t z < 2^{n}

$\ forall n \ in \ mathbb {Z}, z \ in \ mathbb {F_ {2} ^ {n}}: n \ cdot z <2 ^ n$

Somit hat unser Modell eine Berechnungsgrenze. Die Einschränkungen sind im IEEE_754- Standard beschrieben. Ab einem bestimmten Zeitpunkt überschreitet unsere Basisgröße die Genauigkeitsgrenze, und bei der Aufnahme des Moduls werden Fehler erzeugt, die pseudozufälligen Sequenzen ähneln. Dies wird einfach durch Löschen der Zeile überprüft

 if (g < min || g > max) return;

Die endgültige Grenze wird in unserem Fall nach der semi-empirischen Methode berechnet, da wir mit mehreren Parametern arbeiten.

Fazit

Auf den ersten Blick scheinbar weit entfernte Theorien sind also im Browser auf der Leinwand verbunden. Die Konzepte von Aktion, Messung und Berechnung sind eng miteinander verbunden. Das Problem der Kombination ist immer noch nicht gelöst.