Die Diskussionen über die Vor- und Nachteile des neuen revolutionären Posit-Gleitkommaformats dauern an. Das nächste Argument in der Diskussion war die
Aussage, dass die Aufgabe von Posit darin besteht, Daten kompakt zu speichern und überhaupt nicht für Berechnungen zu verwenden. Gleichzeitig werden die Berechnungen selbst in Quire-Arithmetik mit größerer Genauigkeit durchgeführt, was auch im Posit-Standard enthalten ist.
Nun, speichern Sie so speichern. Was bedeutet es, Zahlen nach Berechnungen zu speichern, die mit größerer Genauigkeit durchgeführt wurden, als es das Speicherformat zulässt? Es bedeutet Rundung und Rundung bedeutet Fehler zu machen. Fehler können auf verschiedene Arten geschätzt werden - und um nicht wiederholt zu werden, verwenden wir heute die Spektralanalyse unter Verwendung der Fourier-Transformation.
Sehr kurze Einführung
Wenn wir ein Signal in Form einer Sinuskurve nehmen und eine Fourier-Transformation durchführen, sollten wir im Spektrum einen einzelnen Peak erhalten; Tatsächlich kann das Spektrum sowohl Harmonische mit einer Frequenz enthalten, die ein Vielfaches des Grundtons ist, der als Ergebnis einer nichtlinearen Verzerrung erhalten wird, als auch ein Rauschregal, das als Ergebnis von Rauschen, Interferenz und Digitalisierung erhalten wird. Hier werden wir den Pegel dieser Geräusche messen.
Starten Sie
Um es noch interessanter zu machen, nehmen wir als Testsignal nicht eine Sinuskurve, sondern mehrere; Es muss sichergestellt werden, dass die Perioden dieser Sinuskurven perfekt in die Periode der diskreten Fourier-Transformation passen. In Wolfram Mathematica kann dies beispielsweise folgendermaßen geschehen:
sz = 8192; data = Table[2 Sum[ Sin[Prime[j] k 2 Pi/sz + j*j]/sz, {j, 100, 200, 2}] // N, {k, 0, sz - 1}];
Primzahlen werden hier zur ungleichmäßigen Dezimierung von Frequenzen verwendet; und j * j verschiebt die Phase der Sinuskurve in Abhängigkeit von der Frequenz, um starke Spitzen im Testsignal zu vermeiden und ihm eine mehr oder weniger gleichmäßige Amplitude zu verleihen. Das visuell empfangene Signal sieht folgendermaßen aus:
Als nächstes normalisieren wir es durch den Maximalwert auf Eins und konvertieren es dann in eine Ganzzahl von 32-Bit Int, Float, Posit und erneut in Double. Wenn die Behauptungen der Autoren korrekt sind, ist der durch die Transformation Double → Posit → Double eingeführte Fehler näher an Doublé als an Float.
Wir werden den Rauschpegel in Standardeinheiten für die Signalverarbeitung analysieren - Dezibel, mit denen wir Werte auf einer logarithmischen Skala vergleichen können. Als Werkzeug habe ich meinen eigenen Spektrumanalysator verwendet, der einmal für Forschungszwecke geschrieben wurde.
Also:
blau - schweben
rot - Posit
lila - Int32
blau - doppelt
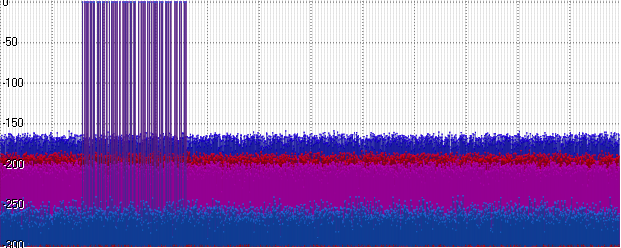
Posit erwies sich natürlich als etwas besser als Float - aber er ist immer noch weit vom Double Level entfernt. Und gleichzeitig - schlimmer als Int32! Es ist logisch - weil ein Teil der Bits eine Größenordnung benötigt ... Verwenden wir diese Reihenfolge - erhöhen Sie die Amplitude unseres Signals auf 1000:
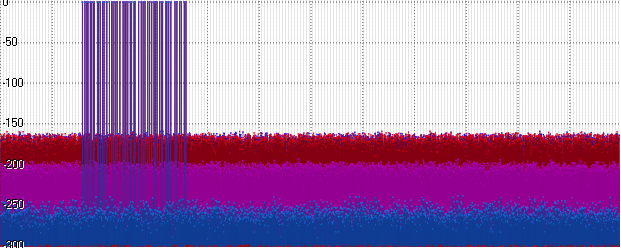
Plötzlich (und eigentlich ziemlich erwartet) holte der Lärm bei Float und Posit auf. Gehen Sie voran - erhöhen Sie die Amplitude auf eine Milliarde:
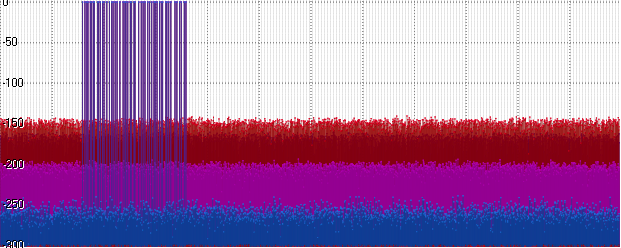
Float zeigt das gleiche Level und Posit beginnt zu verzögern. Eine weitere Erhöhung der Amplitude (hier 10
15 ) führt zu einer weiteren Erhöhung des Rauschregals:
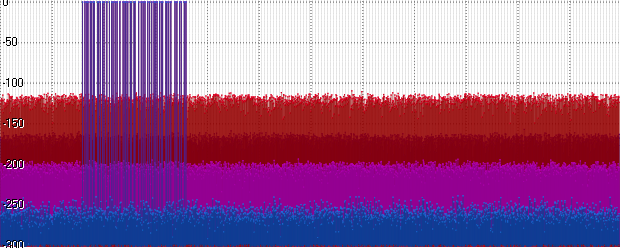
Fazit
Das Wunder geschah immer noch nicht. Die Spektralanalyse bestätigte nicht die Behauptungen der Autoren, dass die Verwendung des Posit-Formats als Speicher eine Genauigkeit nahe Double liefern kann. Selbst unter den besten Bedingungen war das Geräuschregal bei Posit nur 20 Dezibel niedriger als bei Float, aber gleichzeitig um 10 Dezibel höher als bei Int32 und um 60 Dezibel höher als bei Double.
Natürlich kann Posit durchaus eine nützliche Anwendung finden - als Schutz gegen das Überschreiten des zulässigen Bereichs, wenn Emissionen, die die normalen Werte deutlich überschreiten, nicht zu Übersteuerung oder Überlauf führen. Aber auch in diesem Szenario handelt Posit eher wie ein Kompromiss zwischen Int und Float als wie ein deutlich besseres Zahlenformat.