Rätsel auf der Suche nach der perfekten Chance

Gibt es eine objektive, ideale Chance oder ist es das Ergebnis unserer Unwissenheit?

Das Leben ist unvorhersehbar und Unfälle passieren uns ständig. Wir können sagen, dass das Universum selbst zufällig ist. Und doch kann eine große Anzahl zufälliger Ereignisse irgendwie großräumige Muster erzeugen, die die Wissenschaft vorhersagen kann. Wärmeableitung und Brownsche Bewegung sind nur zwei Beispiele für solche Ereignisse.

In letzter Zeit wurde Zufälligkeit sogar in Newsfeeds aufgenommen: Es stellte sich heraus, dass zufällige Oberflächen eine versteckte Reihenfolge haben , und wir haben möglicherweise auch fast gesehen, wie ein Quantencomputer perfekte Zufälligkeit erzeugt . Der letztere Fall, die Suche nach perfekter Zufälligkeit, ist wichtig, da Zufälligkeit Unvorhersehbarkeit mit sich bringt und alle Versuche der Nicht-Quantentechnologie, dies zu erreichen, einen versteckten Fehler aufweisen: Sie werden mithilfe von Algorithmen implementiert, die theoretisch entschlüsselt werden können. In dieser Kolumne lernen wir, wie man Zufälligkeit schafft und im Alltag besiegt, bevor wir zu den philosophischen Höhen der Debatte über das, was wahre Zufälligkeit ist, aufsteigen.

Rätsel 1: zufällige Kombinationen

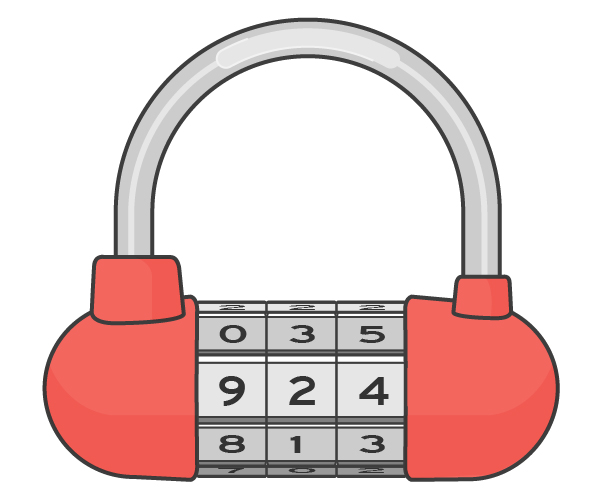
Stellen Sie sich eine einfache Codesperre für ein Fahrrad vor, ähnlich der Abbildung unten. Es hat drei rotierende Scheiben, von denen jede 10 Ziffern in der Reihenfolge anzeigt. Wenn diese drei Scheiben gedreht werden, um die gewünschte Kombination zu erhalten - 924 -, öffnet sich das Schloss. Wenn Sie es schließen möchten, müssen Sie die Zahlen so mischen, dass sie weit von der angegebenen Kombination entfernt sind. Aber was bedeutet "weit" in diesem Zusammenhang? Wenn Sie die Festplatte so weit wie möglich um 5 Positionen bewegen, setzen Sie die Nummer 479. Es ist jedoch für einen Angreifer leicht, versehentlich auf diese Position zu stoßen, wenn er einfach alle fünf Festplatten gleichzeitig dreht und prüft, ob sich das Schloss öffnet. Stellen Sie sich vor, ein Cracker hat Zeit, fünf verschiedene Kombinationen zu testen. In jedem Fall versucht unser potenzieller Dieb unsere Burg nach einer der folgenden Aktionen (und bringt die Burg im Falle eines Fehlers in ihre ursprüngliche Konfiguration zurück):

• Drehen Sie ein Laufwerk an einer zufälligen Anzahl von Positionen.
• Drehen Sie zwei Discs gleichzeitig an einer zufälligen Anzahl von Positionen.
• Drehen Sie alle drei Discs gleichzeitig um eine zufällige Anzahl von Positionen.
• Drehen Sie zwei Discs in unterschiedlichen Winkeln.
• Drehen Sie alle drei Scheiben unterschiedlich.,

Unser Rätsel lautet wie folgt: Wenn der Entsperrcode für das Schloss 924 lautet, welcher Satz gemischter Zahlen ist für zufällige Versuche, das Schloss zu öffnen, am stabilsten, und wie viele solcher Sätze gibt es? Wie hoch ist die Wahrscheinlichkeit, Code zu erkennen?

Rätsel 2: Von der Zufälligkeit zur Reihenfolge in Rätseln

Es überrascht mich oft, wie ähnlich der Prozess der Lösung des Puzzles dem wissenschaftlichen Fortschritt ist. Wir gehen von der Zufälligkeit zur Bestellung über, fügen Teile hinzu, und unser Vertrauen in die Richtigkeit der Lösung wird durch jedes neue geeignete Stück gestärkt. In der zweiten Aufgabe werden wir versuchen, einen Weg zu finden, um unseren Fortschritt auf dem Weg von einem zufälligen ungeordneten Zustand zu einer vollständigen, geordneten Lösung zu messen.



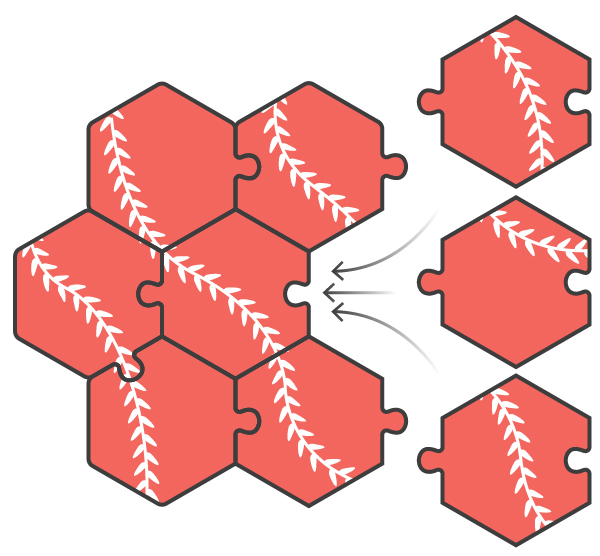
Angenommen, wir lösen ein Puzzle, das aus sechseckigen Teilen besteht - wie Waben. Das Bild des Puzzles ist eine gewundene Rebe. Da sich das Muster wiederholt und selbstähnlich ist, kann nicht garantiert werden, dass zwei benachbarte Teile physisch zueinander passen, selbst wenn sie in das Bild passen. Angenommen, drei andere können zu jeder Kante eines bestimmten Stücks gehen. Wenn also zwei Teile im Bild zueinander passen, beträgt die Wahrscheinlichkeit, dass sie physisch passen, 33,33%. Wenn Sie jedoch ein anderes Stück finden, das zu beiden passt, dh eines, das mit beiden einen gemeinsamen Vorteil hat, steigt Ihr Vertrauen in den Erfolg. Versuchen wir zu bewerten, wie viel es wächst.

1. Sie haben drei Teile gefunden, die auf den ersten Blick zusammenpassen, ohne dass das Lianenmuster an den angrenzenden Kanten offensichtlich verschoben ist. Was ist das Maß für Ihr Vertrauen in die richtige Auswahl der Stücke?
2. Sie haben ein zentrales sechseckiges Stück gefunden und sechs, die es umgeben, und auf dem Bild scheinen sie zusammenzufallen. Was ist das Maß für Ihr Vertrauen in die richtige Auswahl der Stücke?

Je größer die Stückgruppen werden, desto stärker ist Ihr Vertrauen in die richtige Montage. Es ist anzunehmen, dass drei isolierte Gruppen, in denen es insgesamt sieben verbundene Teile gibt, nicht mit dem oben beschriebenen einzigen umgebenden Sechseck vergleichbar sind.

Der dritte Teil dieses Rätsels enthält Korrekturen und ist ein Versuch, den obigen Unterschied zu quantifizieren. Ist es möglich, ein Maß für den Fertigstellungsgrad eines teilweise gelösten Puzzles zu finden? Diese Methode sollte es Ihnen ermöglichen, jedem teilweise zusammengesetzten Puzzle mit 10x10 Sechsecken eine Zahl von 0 bis 100 zuzuweisen. Diese Zahl sollte den Fertigstellungsgrad angeben und in etwa mit dem Anteil des aktuellen Status des Puzzles an der fertigen Version korrelieren.

Rätsel 3: Ist ein perfekter Zufall möglich?

In diesem Teil werde ich Ihnen eine Variante der berühmten Einstein-Bohr-Debatte für den Zufall geben. Debattenteilnehmer können sich den Teams E oder B anschließen.

Beide Teams sind sich einig, dass im Makrokosmos die Existenz von zufällig erzeugenden Mechanismen nur möglich ist, weil wir die Kräfte oder die ihnen zugrunde liegenden Algorithmen nicht verstehen. Wenn Sie alle Kräfte kennen, die auf eine umgedrehte Münze oder einen Würfel wirken, wenn Sie über ausreichende Rechenleistung verfügen, können Sie das Ergebnis vorhersagen. Entsprechend der Verbreitung der Ansichten von Team B wird uns beigebracht, dass dies in der Quantenwelt nicht der Fall ist - Quantenwahrscheinlichkeiten sollten objektiv sein. Aber ist das überhaupt möglich? Könnte es in der subquantischen Planck-Welt einen Mechanismus geben, der entscheidet, welche der beiden gleich wahrscheinlichen Optionen implementiert wird, selbst wenn wir nie die Möglichkeit haben, dieses Niveau zu studieren? Selbst wenn Einsteins Albtraum mit einem Würfelspiel real ist, sollte diese Gottheit einen Algorithmus im Kopf haben, der jede Wahl entscheidet, egal wie bizarr und unlogisch. Dann wird der Zufall wieder auf unsere Unwissenheit zurückzuführen sein. Es wird nur in der Praxis unbekannt und nicht zufällig objektiv sein.

Die Standardantwort von Team B ist, dass die Quantenwelt einfach zu seltsam ist, um die Regeln anzuwenden, die wir aus unserer Erfahrung im Umgang mit dem Makrokosmos gelernt haben. Es gibt jedoch zwei Arten von Kuriositäten. Einerseits kann Fremdheit in der physischen Unmöglichkeit liegen, sich schneller als mit Lichtgeschwindigkeit zu bewegen. Eine solche Seltsamkeit kann existieren, und es wird nur bedeuten, dass wir unser Verständnis des physikalischen Gesetzes unter besonderen Umständen überdenken müssen, so wie Einstein das Gesetz der Addition von Newtons Geschwindigkeiten überarbeitet hat, das bei sehr großen Werten falsch wird.

Andererseits kann etwas in Bezug auf die logische Unmöglichkeit seltsam sein - wie 2 + 2 gleich 5. Ein solches Ergebnis ist in keinem Universum unmöglich. Team E könnte argumentieren, dass perfekte Zufälle und objektive Wahrscheinlichkeiten logisch unmöglich sind. Wir sollten sie nicht akzeptieren, sondern müssen physikalische Mechanismen finden, die die beobachteten Ergebnisse erklären können, unabhängig davon, gegen welche bestehenden Gesetze der Physik sie verstoßen könnten.

Zu welchem ​​Team gehören Sie?

PS: Antworten werden später veröffentlicht.