Diejenigen, die mit Daten arbeiten, sind sich bewusst, dass das Glück nicht im neuronalen Netzwerk liegt, sondern darin, wie die Daten richtig verarbeitet werden. Um sie zu verarbeiten, müssen Sie jedoch zuerst die Korrelationen analysieren, die erforderlichen Daten auswählen, das Unnötige wegwerfen und so weiter. Für solche Zwecke wird häufig eine Visualisierung unter Verwendung der matplotlib-Bibliothek verwendet.
Triff mich "drinnen"!
Anpassung
Führen Sie den folgenden Code zum Konfigurieren aus. Einzelne Diagramme überschreiben jedoch ihre Einstellungen selbst.
Korrelation
Korrelationsdiagramme werden verwendet, um die Beziehung zwischen zwei oder mehr Variablen zu visualisieren. Das heißt, wie sich eine Variable im Verhältnis zu einer anderen ändert.
1. Streudiagramm
Scatteplot ist eine klassische und grundlegende Diagrammansicht, mit der die Beziehung zwischen zwei Variablen untersucht wird. Wenn Ihre Daten mehrere Gruppen enthalten, können Sie jede Gruppe in einer anderen Farbe anzeigen. In matplotlib können Sie dies einfach mit plt.scatterplot () tun.

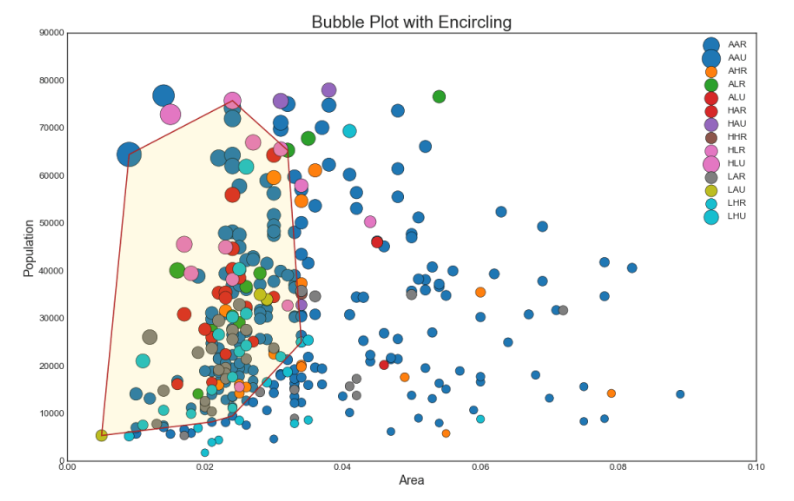
2. Blasendiagramm mit Gruppenerfassung
Manchmal möchten Sie eine Gruppe von Punkten innerhalb des Rahmens anzeigen, um deren Bedeutung hervorzuheben. In diesem Beispiel erhalten wir die Datensätze aus dem Datenrahmen, die zugewiesen werden sollen, und übergeben sie an encircle (), wie im folgenden Code beschrieben.
Code anzeigen from matplotlib import patches from scipy.spatial import ConvexHull import warnings; warnings.simplefilter('ignore') sns.set_style("white")
3. Am besten passender linearer Regressionsgraph
Wenn Sie verstehen möchten, wie sich zwei Variablen im Verhältnis zueinander ändern, ist die Best-Fit-Linie am besten. Die folgende Grafik zeigt, wie sich die beste Anpassung zwischen verschiedenen Datengruppen unterscheidet. Um Gruppierungen zu deaktivieren und einfach eine Best-Fit-Linie für den gesamten Datensatz zu zeichnen, entfernen Sie den Parameter hue = 'cyl' aus sns.lmplot () unten.

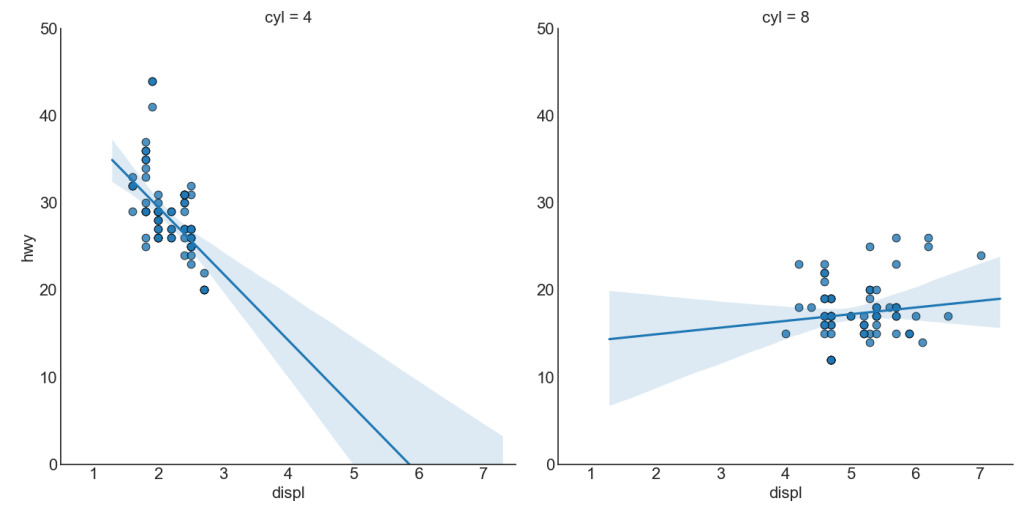
Jede Regressionszeile in einer eigenen Spalte
Darüber hinaus können Sie die am besten passende Linie für jede Gruppe in einer separaten Spalte anzeigen. Sie möchten dies tun, indem Sie den Parameter col = groupingcolumn in sns.lmplot () festlegen.
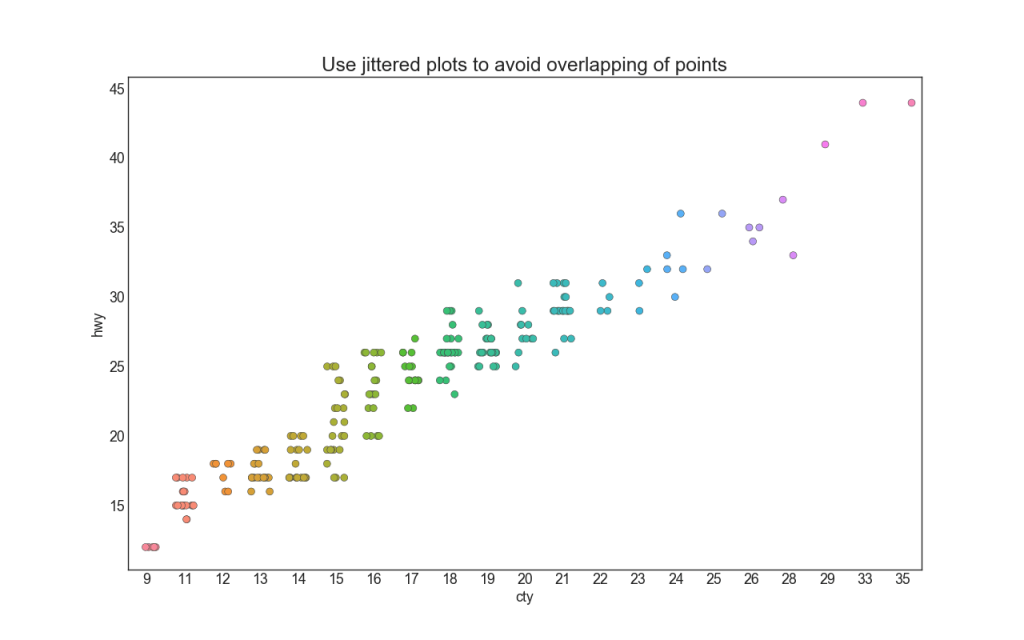
4. Stripplot
Oft haben mehrere Datenpunkte die gleichen X- und Y-Werte. Infolgedessen werden mehrere Datenpunkte übereinander gezeichnet und ausgeblendet. Um dies zu vermeiden, bewegen Sie die Punkte leicht auseinander, damit Sie sie visuell sehen können. Dies geschieht bequem mit stripplot ().
5. Zählplot
Eine andere Option, die das Problem überlappender Punkte vermeidet, besteht darin, den Punkt zu vergrößern, je nachdem, wie viele Punkte an dieser Stelle liegen. Je größer der Punkt ist, desto größer ist die Konzentration der Punkte um ihn herum.

6. Ein Balkendiagramm
Linienhistogramme haben ein Histogramm entlang der Variablen der X- und Y-Achse. Dies wird verwendet, um die Beziehung zwischen X und Y zusammen mit der eindimensionalen Verteilung von X und Y einzeln zu visualisieren. Dieses Diagramm wird häufig in der Datenanalyse (EDA) verwendet.
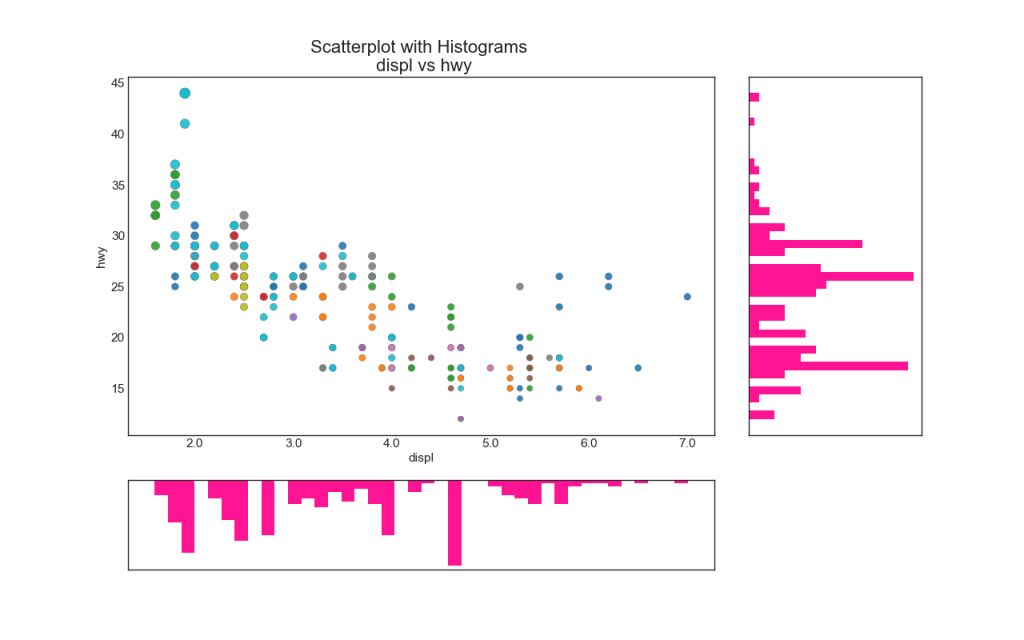
7. Boxplot
Boxplot dient demselben Zweck wie ein zeilenweises Histogramm. Dieses Diagramm hilft jedoch dabei, den Median, das 25. und das 75. Perzentil von X und Y zu bestimmen.
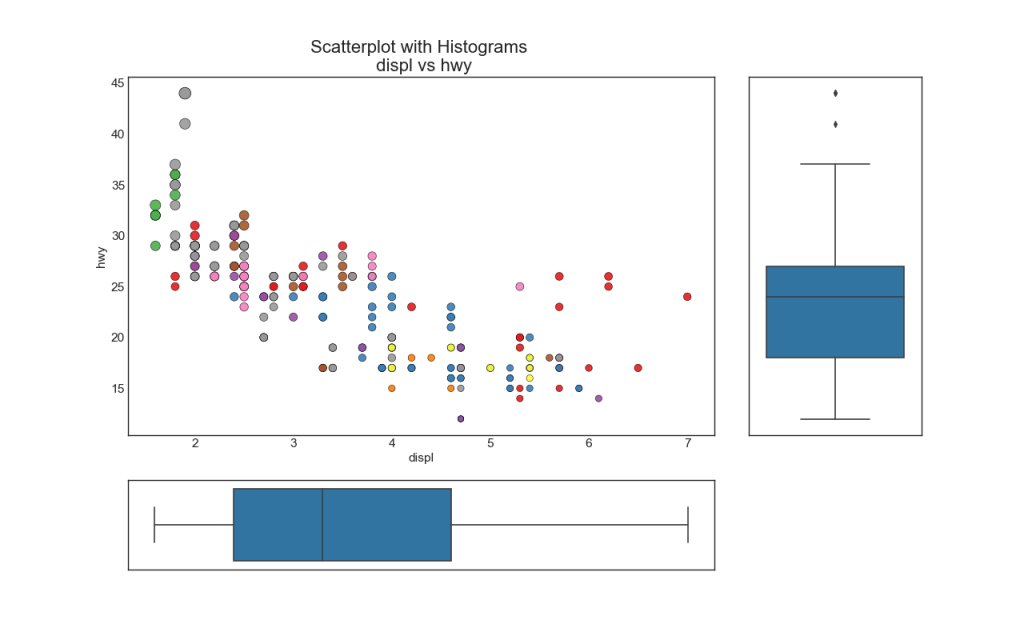
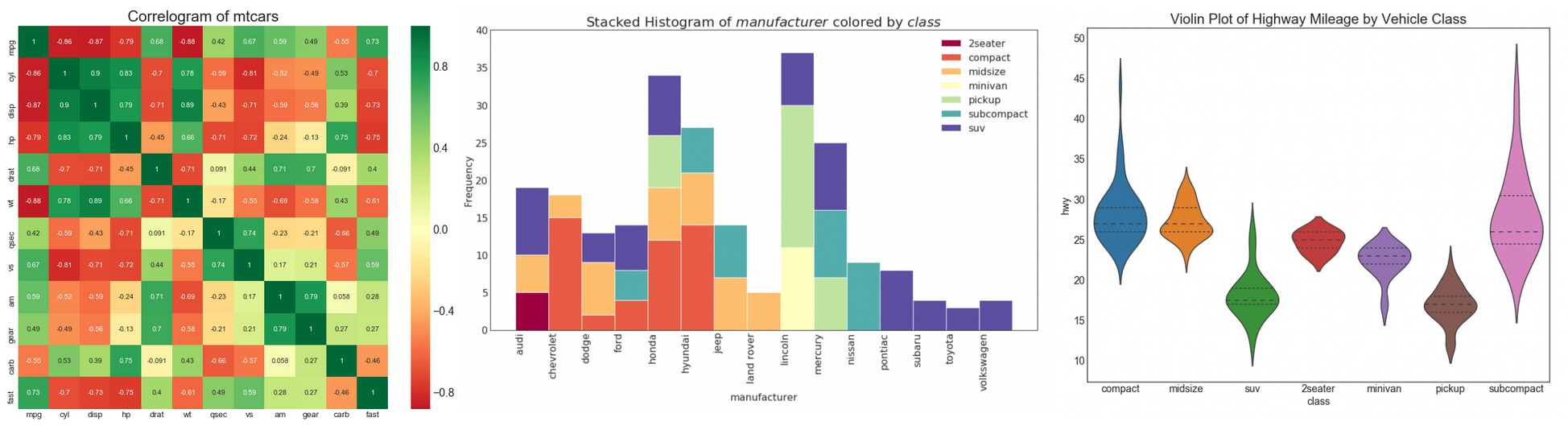
8. Das Korrelationsdiagramm
Das Korrelationsdiagramm wird verwendet, um die Korrelationsmetrik zwischen allen möglichen Paaren numerischer Variablen in einem bestimmten Datensatz (oder zweidimensionalen Array) visuell anzuzeigen.
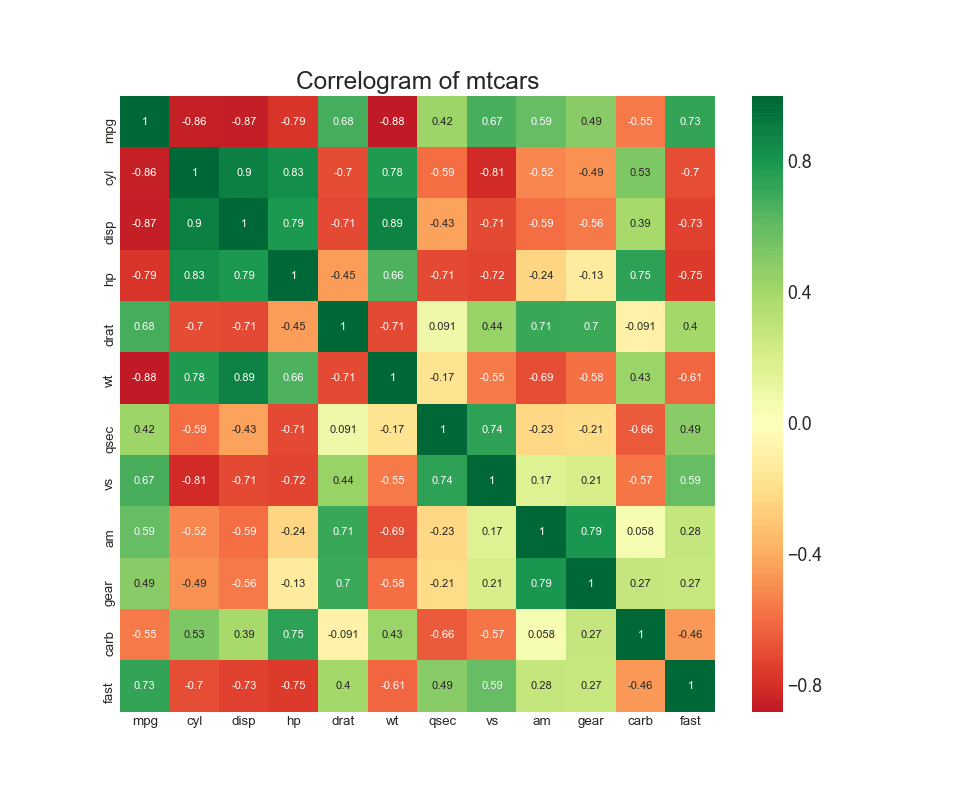
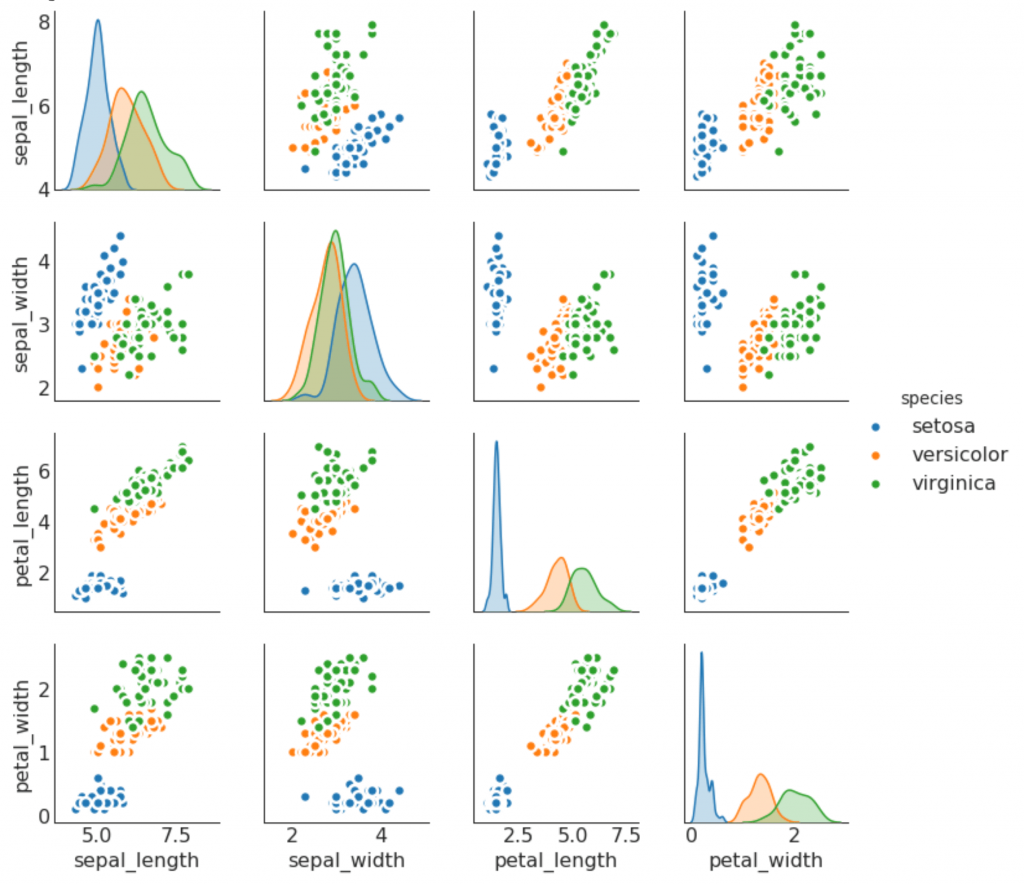
9. Pair-Zeitplan
Wird häufig in der Forschungsanalyse verwendet, um die Beziehung zwischen allen möglichen Paaren numerischer Variablen zu verstehen. Dies ist ein Muss für die zweidimensionale Analyse.
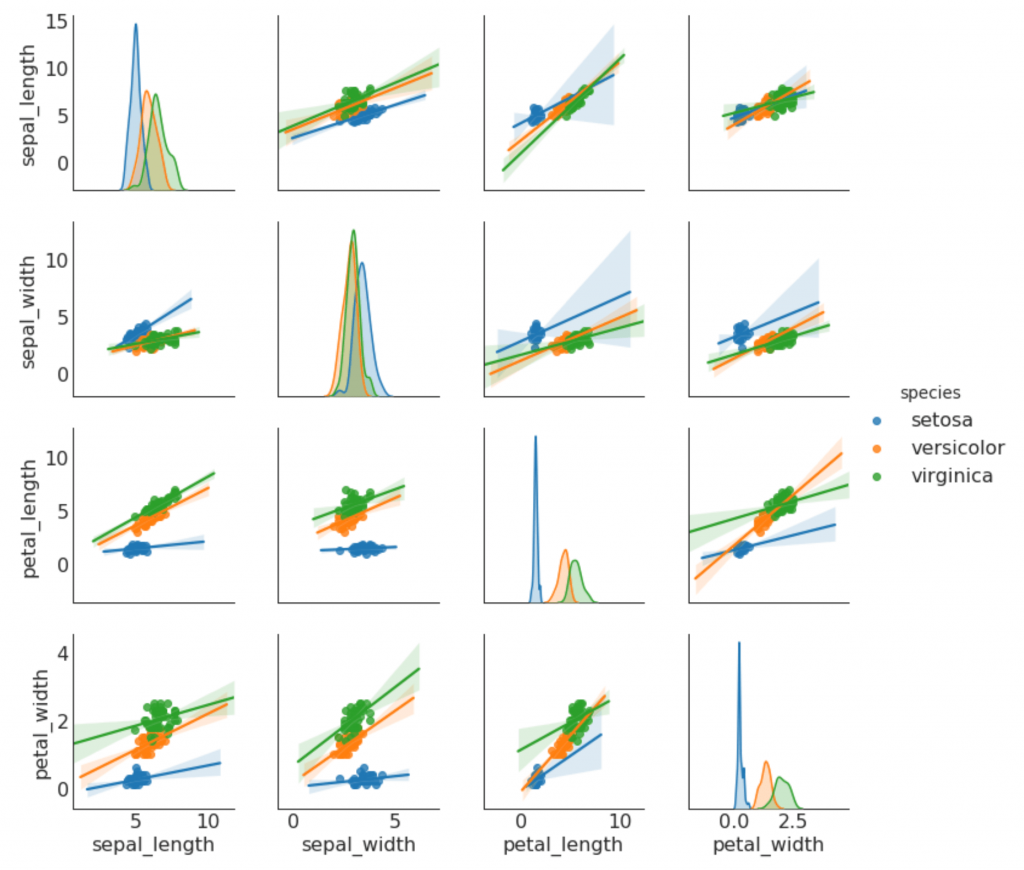
Abweichung
10. Abweichende Spalten
Wenn Sie sehen möchten, wie sich die Elemente in Abhängigkeit von einer Metrik ändern, und die Reihenfolge und Größe dieser Streuung visualisieren möchten, sind divergierende Spalten ein hervorragendes Werkzeug. Es hilft, die Leistung von Gruppen in Ihren Daten schnell zu unterscheiden, ist sehr intuitiv und vermittelt sofort Bedeutung.

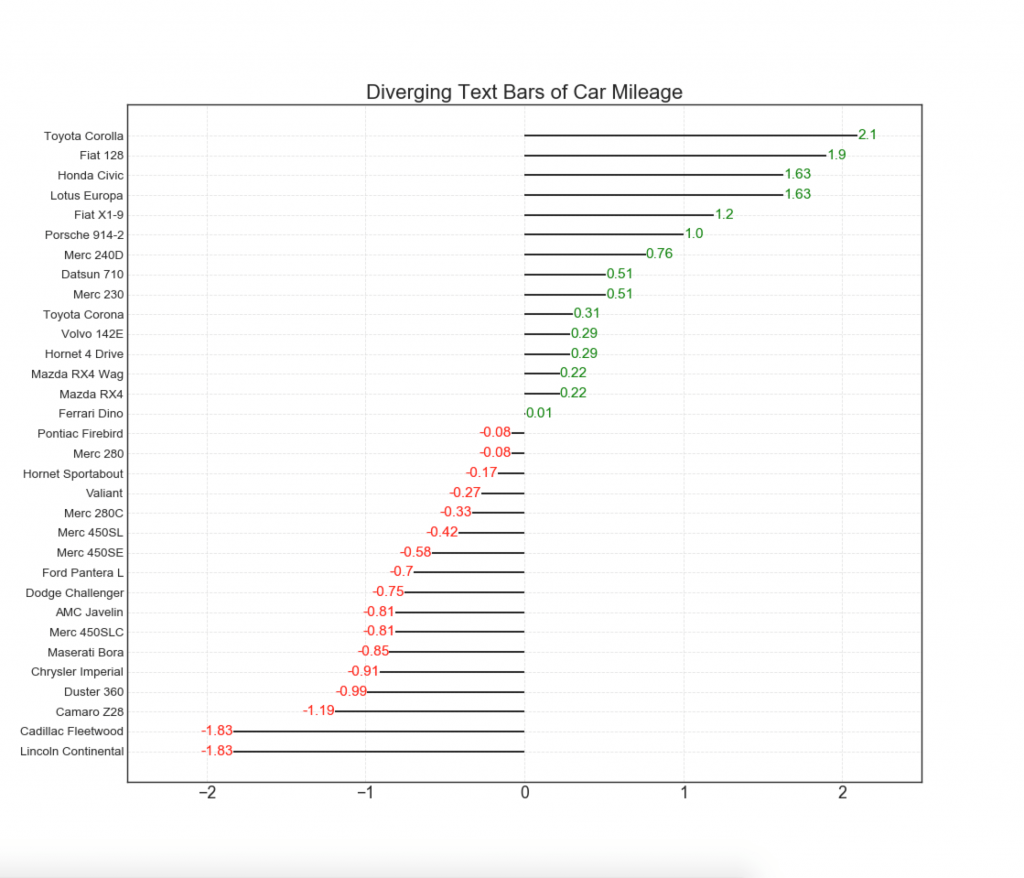
11. Abweichende Spalten mit Text
- Sieht aus wie divergierende Spalten. Dies ist vorzuziehen, wenn Sie die Bedeutung jedes Elements im Diagramm auf gute und präsentable Weise darstellen möchten.
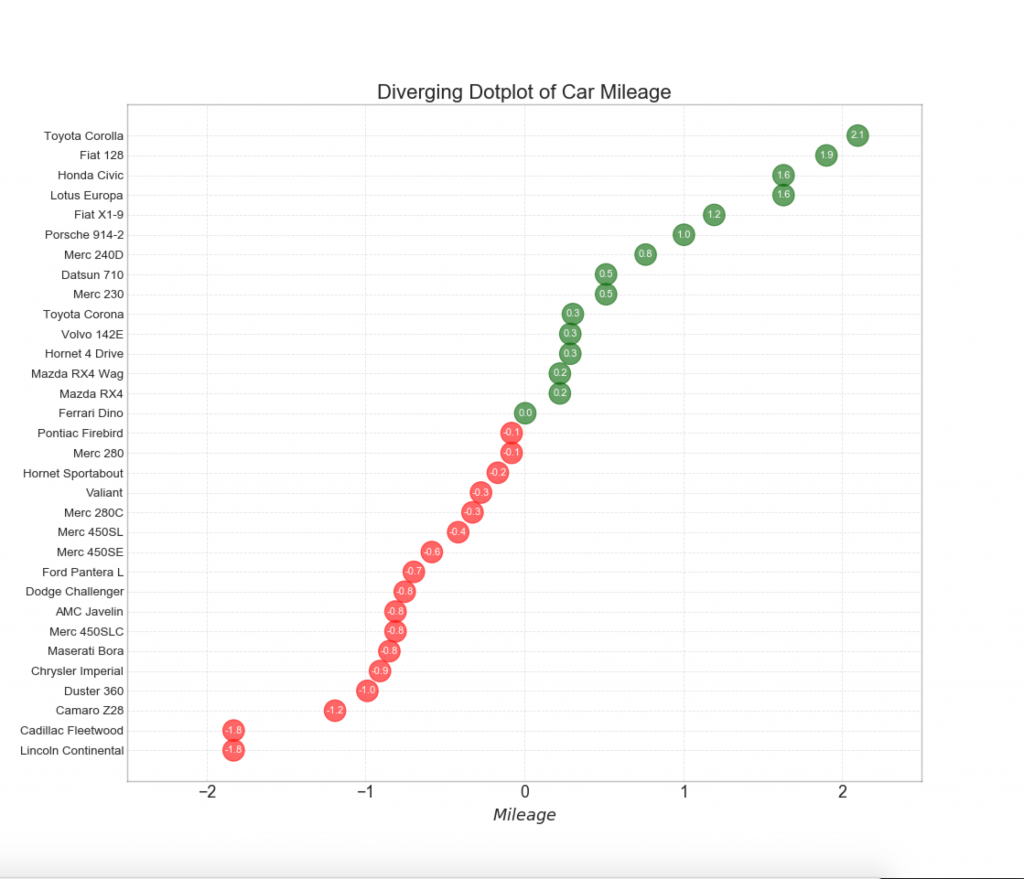
12. Abweichende Punkte
Das Diagramm der divergierenden Punkte ähnelt auch divergierenden Spalten. Im Vergleich zu divergierenden Spalten verringert das Fehlen von Spalten jedoch den Kontrast und die Diskrepanz zwischen den Gruppen.
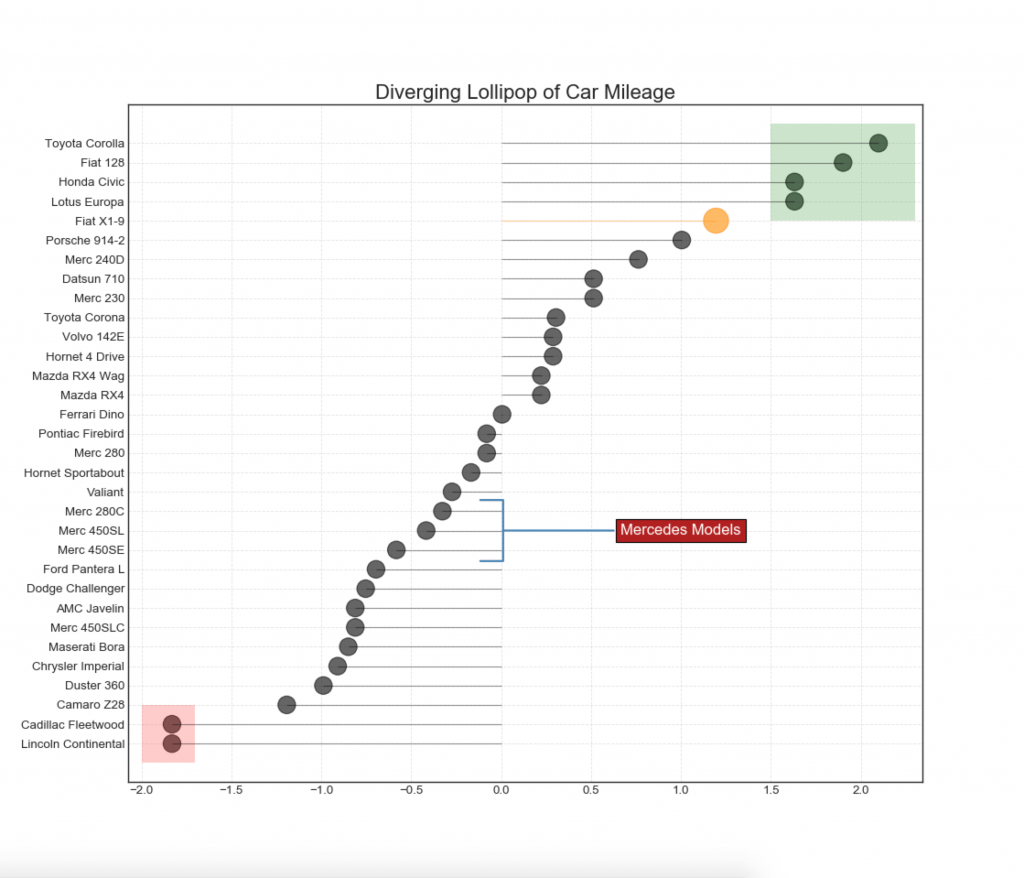
13. Divergentes Lollipop-Diagramm mit Markierungen
Lollipop bietet eine flexible Möglichkeit, Diskrepanzen zu visualisieren und sich auf alle relevanten Datenpunkte zu konzentrieren, auf die Sie achten möchten.
14. Flächendiagramm
Das Flächendiagramm färbt den Bereich zwischen der Achse und den Linien und betont Spitzen und Täler, aber auch die Dauer der Höhen und Tiefen. Je länger die Höhen sind, desto größer ist der Bereich unter der Linie.
Code anzeigen import numpy as np import pandas as pd
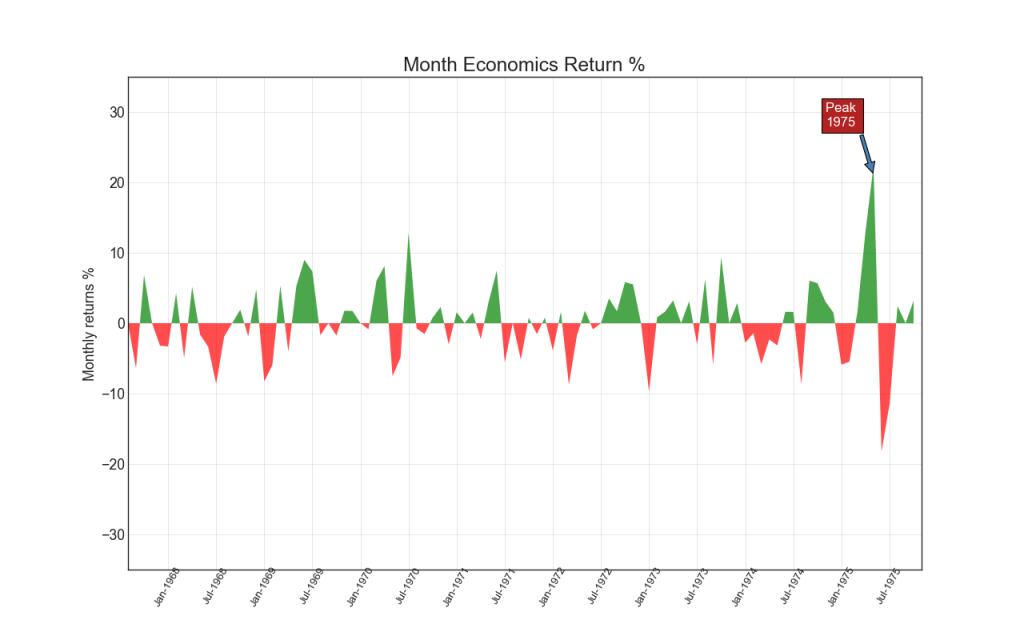
Rangliste
15. Geordnetes Histogramm
Ein geordnetes Histogramm vermittelt effektiv die Rangfolge der Elemente. Durch Hinzufügen eines Metrikwerts über dem Diagramm erhält der Benutzer jedoch genaue Informationen aus dem Diagramm selbst.
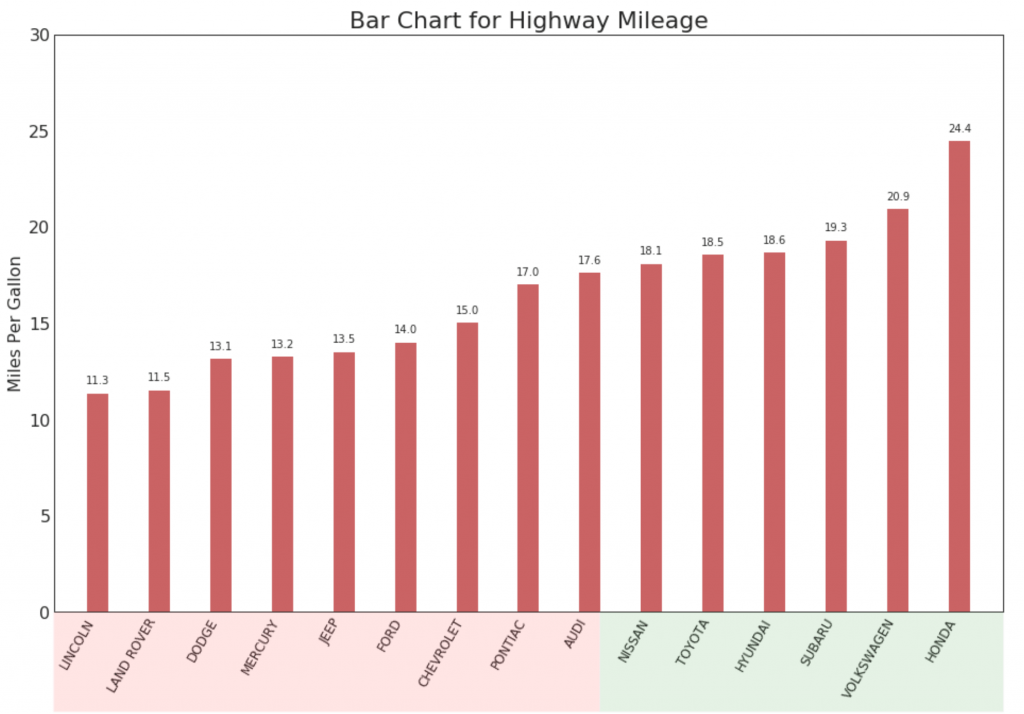
16. Lutschertabelle
Das Lollipop-Diagramm dient auf visuell ansprechende Weise einem ähnlichen Zweck wie ein geordnetes Histogramm.
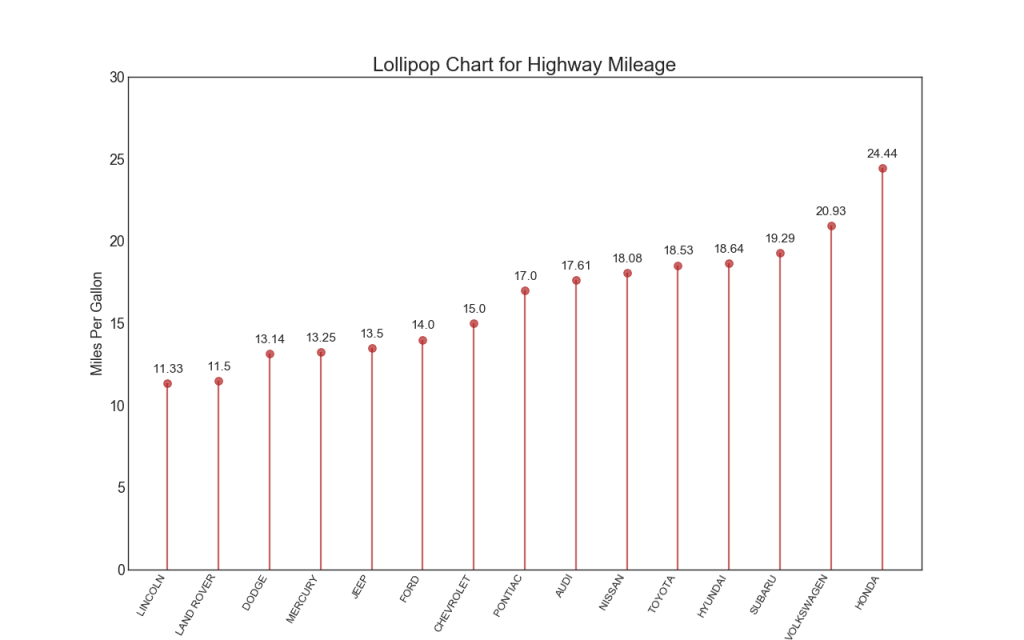
17. Gepunktete Tabelle mit Unterschriften
Ein Streudiagramm vermittelt die Rangfolge der Elemente. Und da es entlang der horizontalen Achse ausgerichtet ist, können Sie visuell bewerten, wie weit die Punkte voneinander entfernt sind.
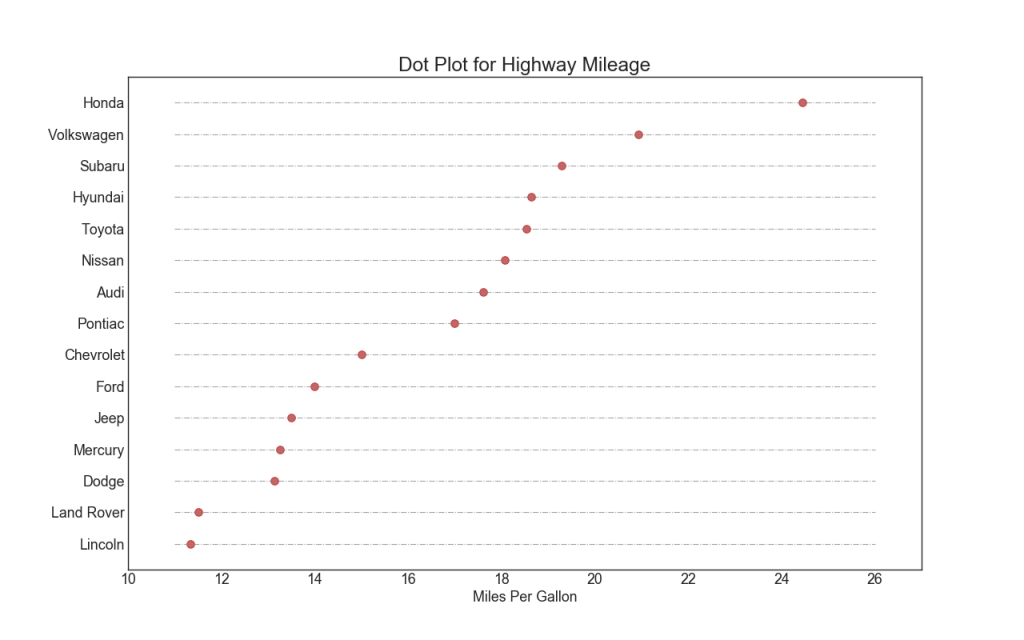
18. Schräge Karte
Das Steigungsdiagramm eignet sich am besten zum Vergleichen der Positionen „Vorher“ und „Nachher“ einer bestimmten Person / eines bestimmten Subjekts.
Code anzeigen import matplotlib.lines as mlines

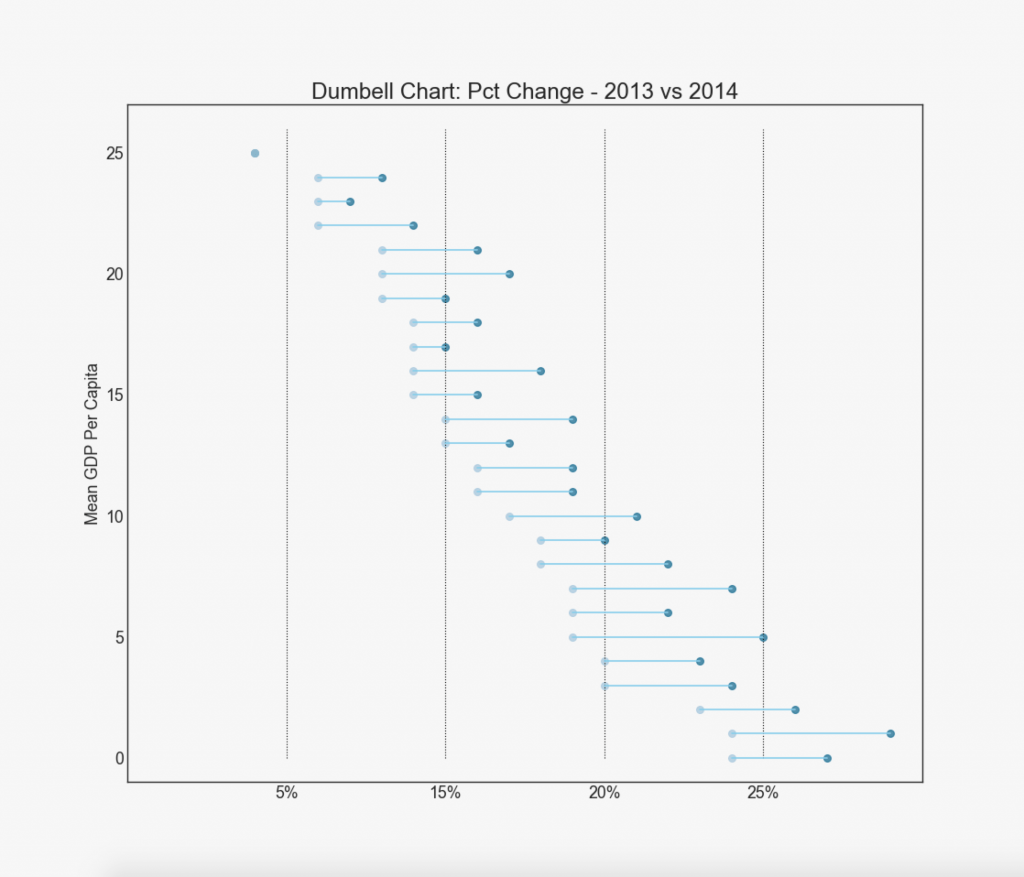
19. "Hanteln"
Das Diagramm „Hantel“ zeigt die Positionen „Vorher“ und „Nachher“ verschiedener Einflüsse sowie die Rangfolge der Elemente. Dies ist sehr nützlich, wenn Sie die Auswirkung von etwas auf verschiedene Objekte visualisieren möchten.
Code anzeigen import matplotlib.lines as mlines
Verteilung
20. Histogramm für eine kontinuierliche Variable
Das Histogramm zeigt die Häufigkeitsverteilung dieser Variablen. In der folgenden Präsentation werden Frequenzbänder anhand einer kategorialen Variablen gruppiert.
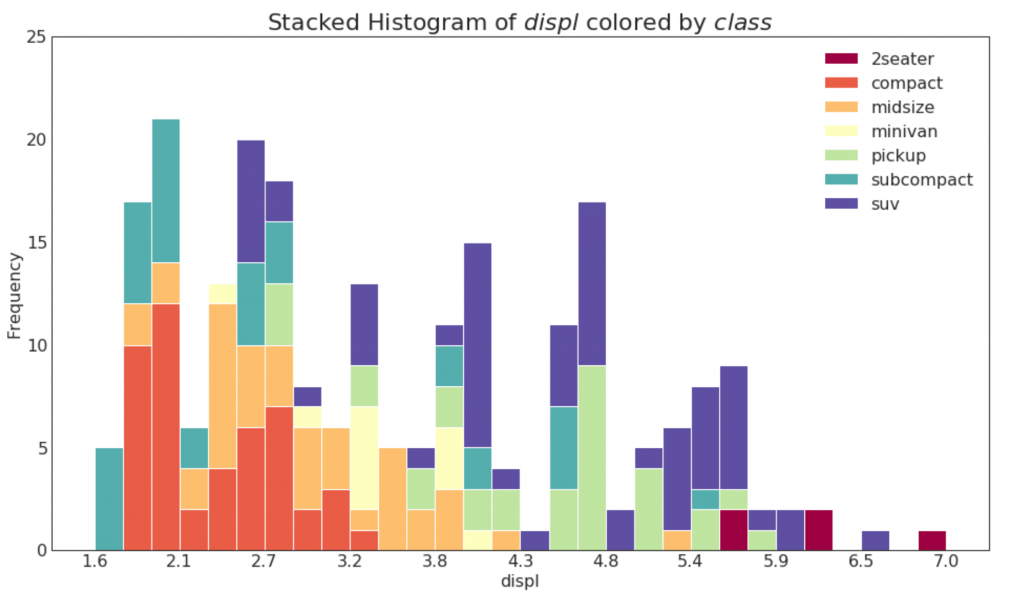
21. Histogramm für eine kategoriale Variable
Das Histogramm einer kategorialen Variablen zeigt die Häufigkeitsverteilung dieser Variablen. Durch Färben der Spalten können Sie die Verteilung in Bezug auf eine andere kategoriale Variable visualisieren, die Farben darstellt.
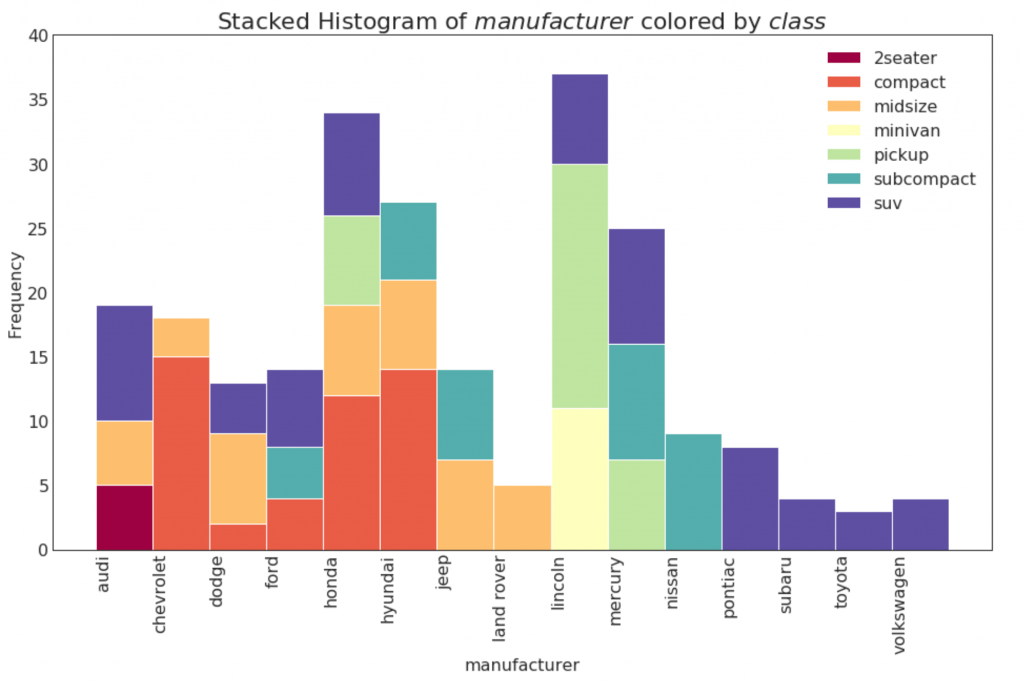
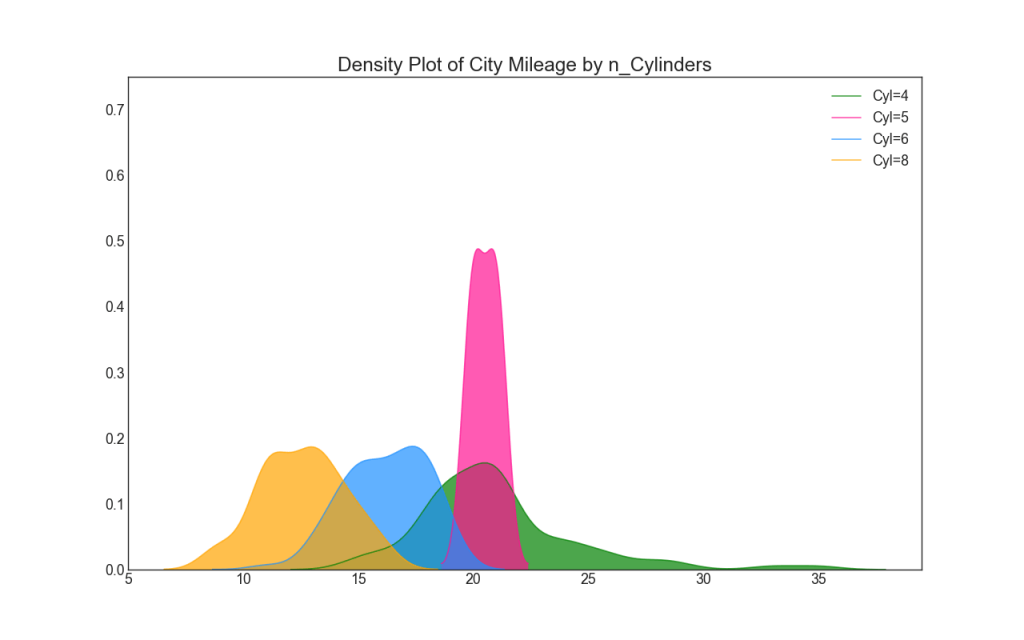
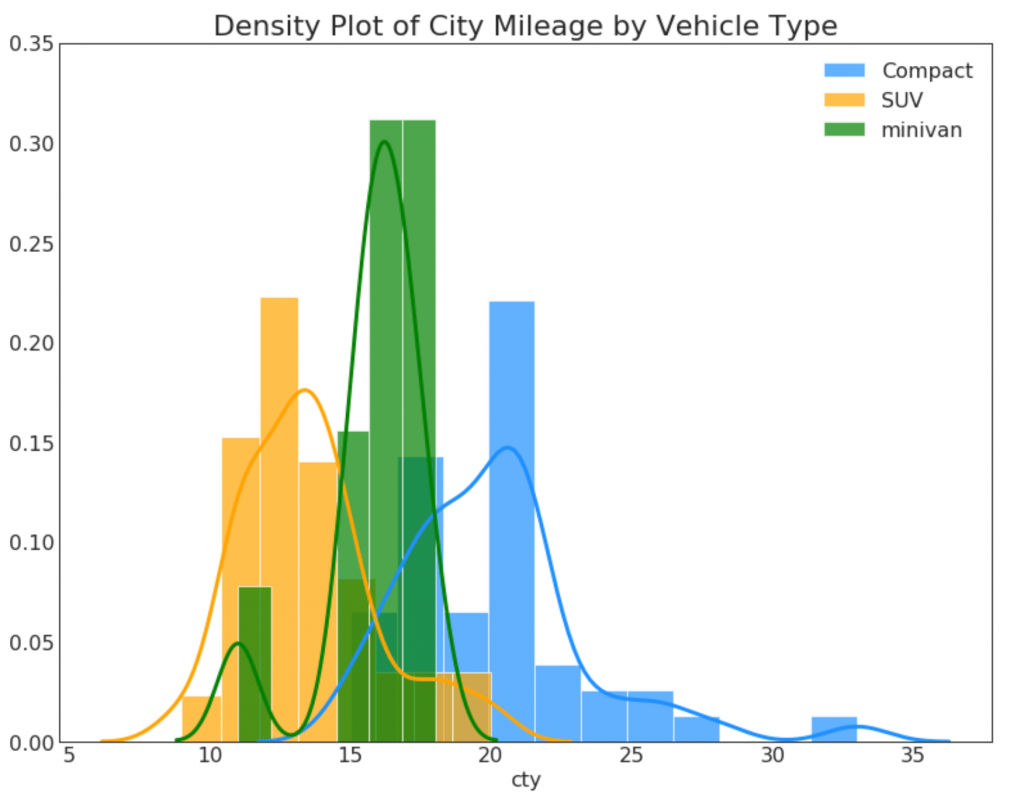
22. Dichtediagramm
Dichtediagramme sind ein weit verbreitetes Werkzeug zur Visualisierung der Verteilung einer kontinuierlichen Variablen. Nachdem Sie sie nach der Variablen „Antwort“ gruppiert haben, können Sie die Beziehung zwischen X und Y überprüfen. Im Folgenden finden Sie ein Beispiel, wenn wir der Übersichtlichkeit halber beschreiben, wie sich die Verteilung der Kilometer in der Stadt in Abhängigkeit von der Anzahl der Zylinder ändert.
23.
, , .
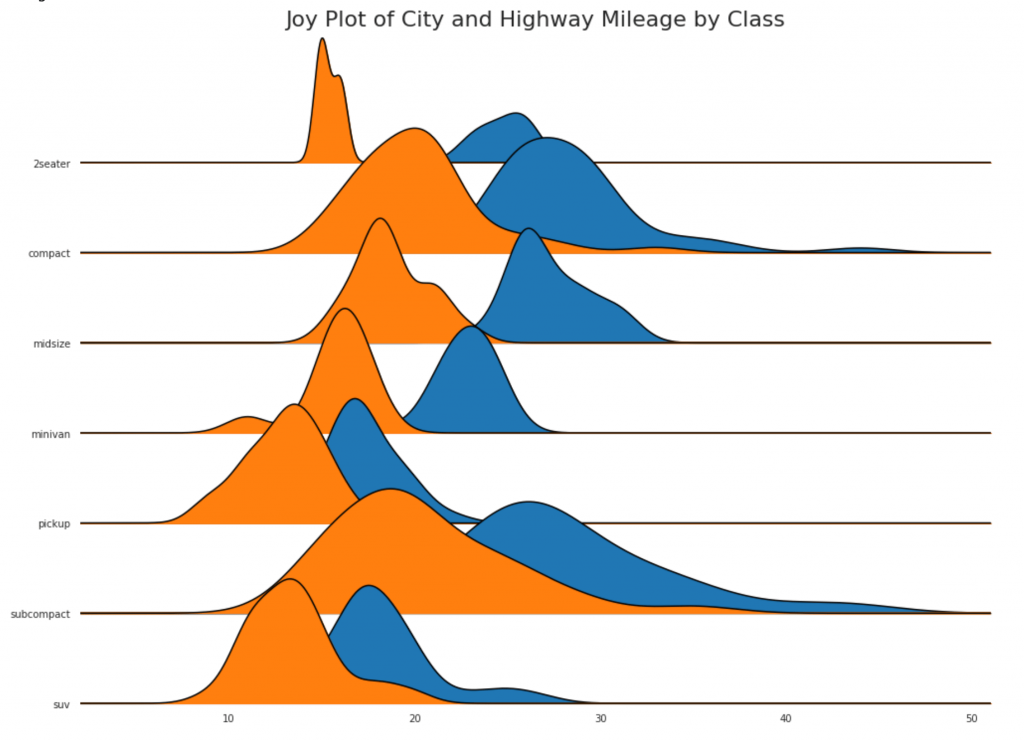
24. Joy
Joy , . .
25.
, . , . - , .
import matplotlib.patches as mpatches

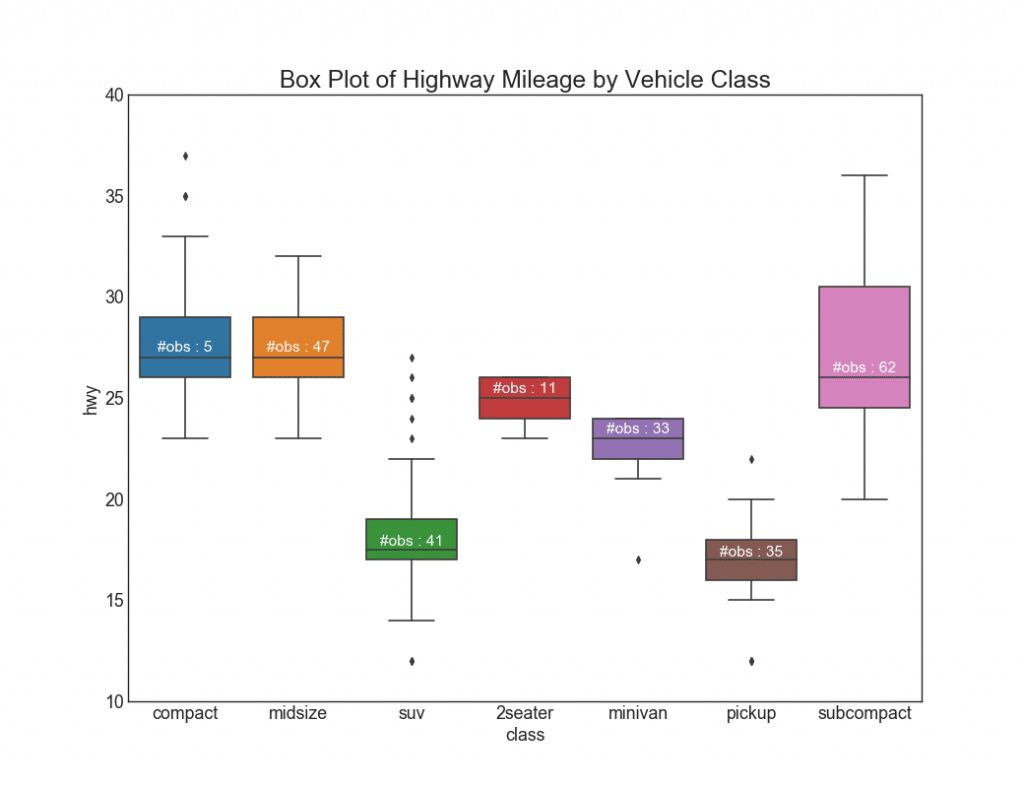
26.
— , , 25-, 75- . , , . , .
, , 5 47 . .
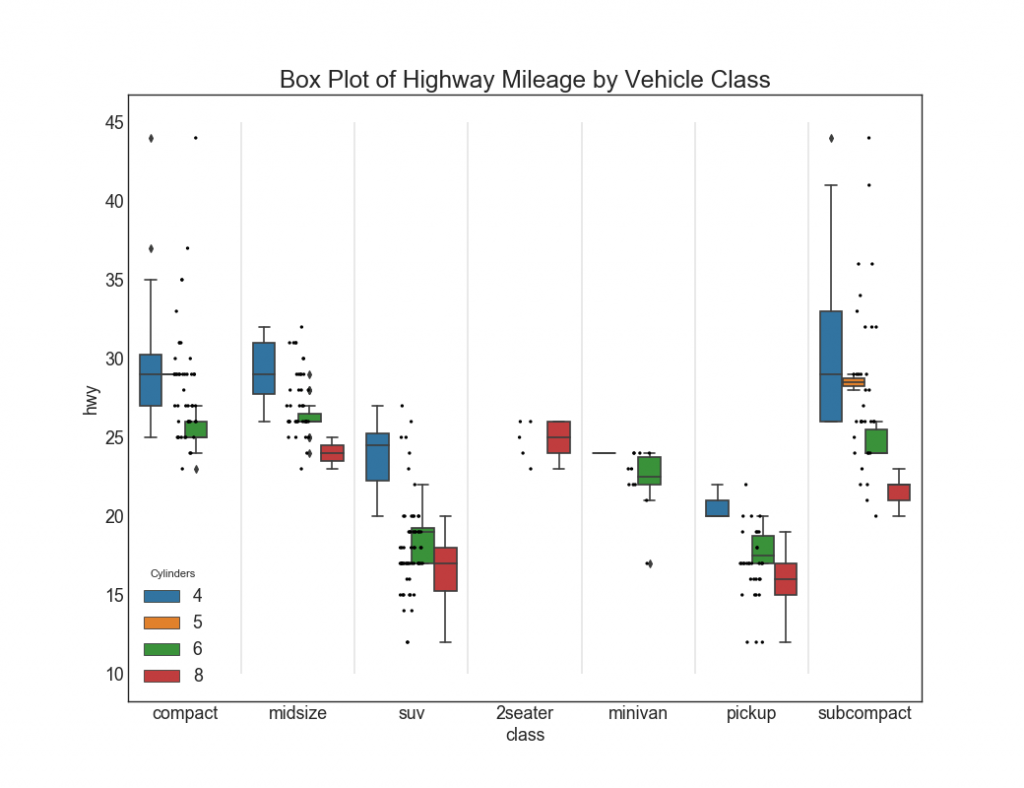
27.
Dot + Box plot , boxplot, . , .
28. «»
Ein solcher Zeitplan ist eine optisch ansprechende Alternative zum Boxplot. Die Form oder Fläche der „Geige“ hängt von der Datenmenge in dieser Gruppe ab. Solche Grafiken können jedoch schwieriger zu lesen sein und werden normalerweise nicht in professionellen Umgebungen verwendet.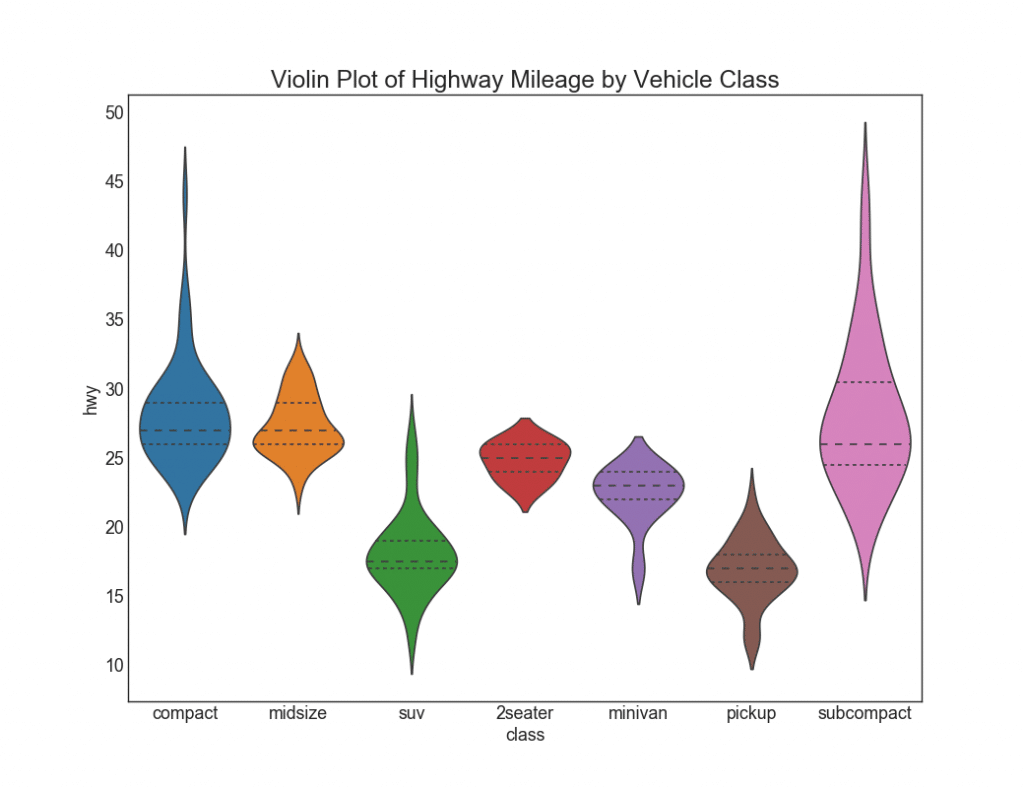
29. Pyramide der Bevölkerung
Eine Bevölkerungspyramide kann verwendet werden, um die Verteilung der nach Volumen geordneten Gruppen anzuzeigen oder um die schrittweise Filterung der Bevölkerung anzuzeigen, wie unten gezeigt, um zu visualisieren, wie viele Personen jede Phase des Marketing-Trichters durchlaufen.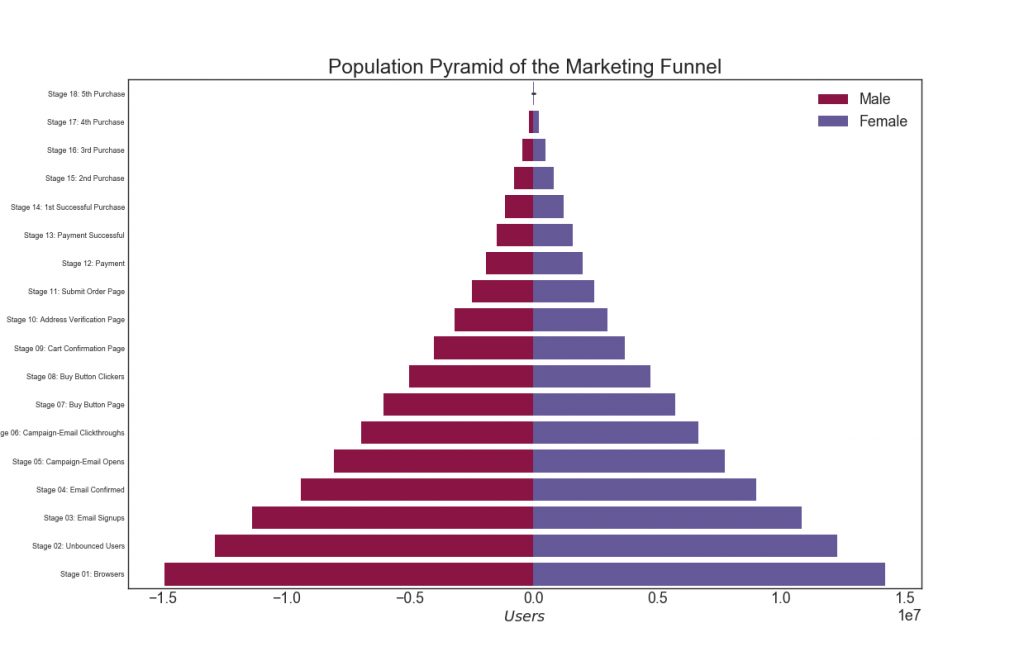
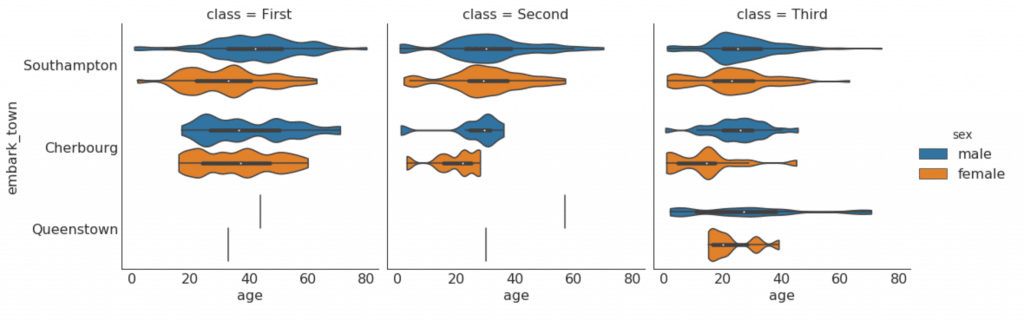
30. Kategoriale Diagramme
Die von der Seaborn-Bibliothek bereitgestellten kategorialen Diagramme können verwendet werden, um die Verteilung der Anzahl von zwei oder mehr kategorialen Variablen relativ zueinander zu visualisieren.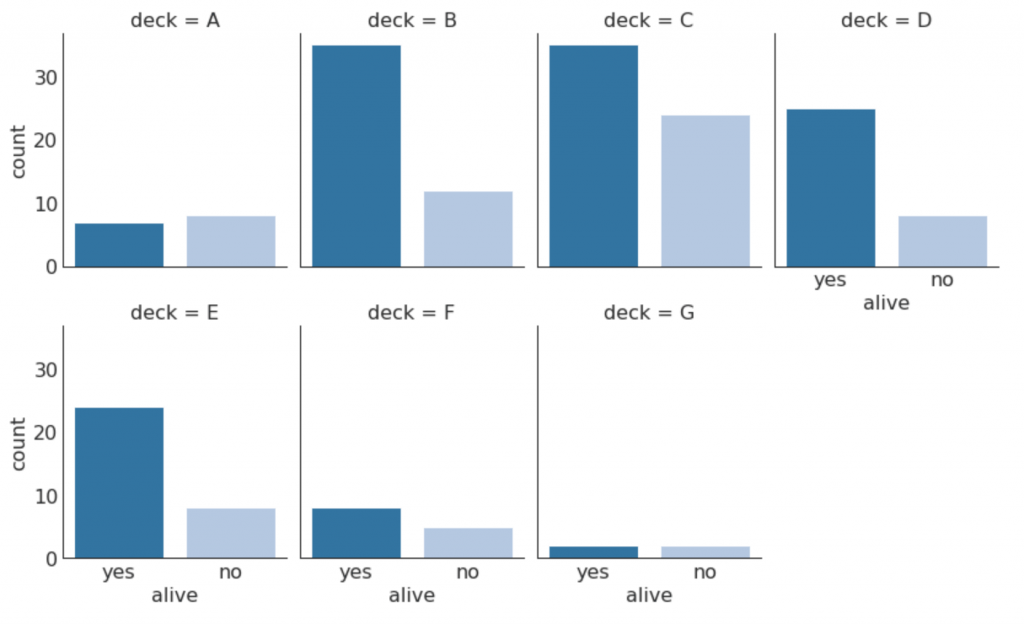
Montage, Zusammensetzung
31. Waffeldiagramm
Mit dem Pywaffelpaket kann ein Waffeldiagramm erstellt werden, mit dem Gruppenzusammensetzungen in den meisten Bevölkerungsgruppen angezeigt werden.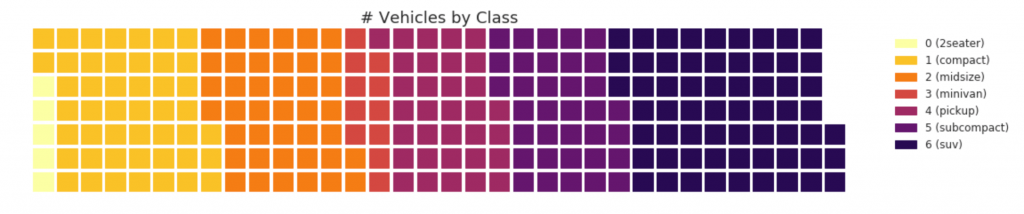
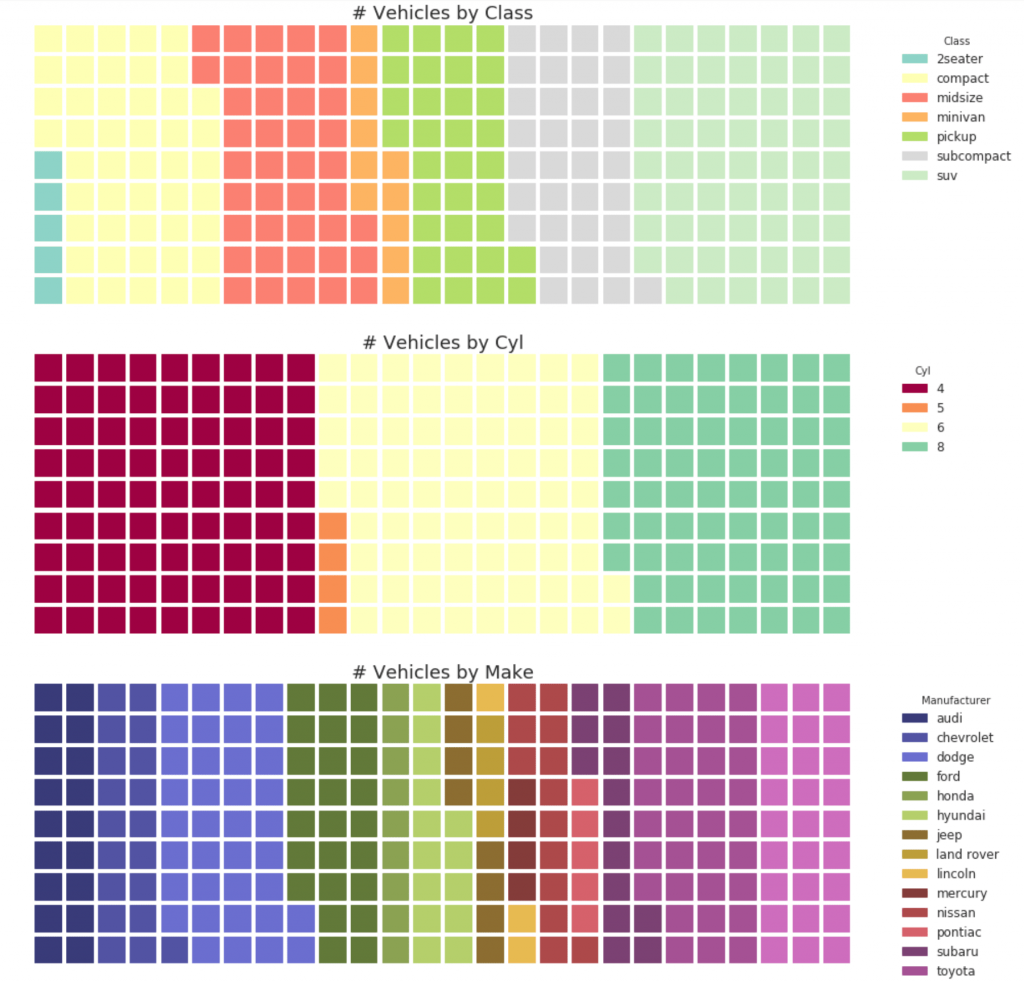
32. Kreisdiagramm
Ein Kreisdiagramm ist eine klassische Methode, um die Zusammensetzung von Gruppen anzuzeigen. Es wird jedoch derzeit im Allgemeinen nicht empfohlen, dieses Diagramm zu verwenden, da der Bereich der Segmente manchmal irreführend sein kann. Wenn Sie ein Kreisdiagramm verwenden möchten, wird daher dringend empfohlen, den Prozentsatz oder die Zahl für jeden Teil des Kreisdiagramms explizit aufzuzeichnen.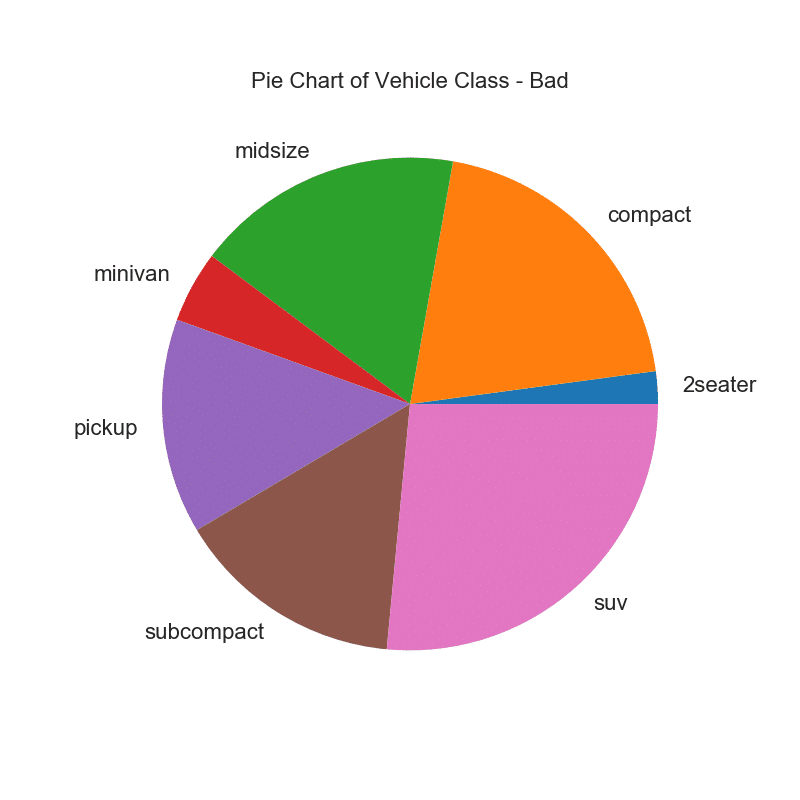
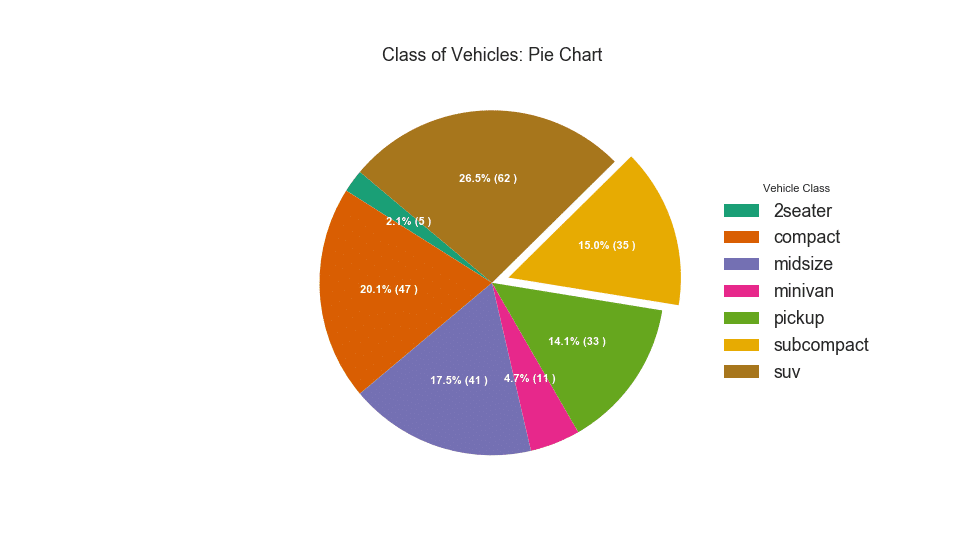
33. Baumkarte
Die Baumkarte sieht aus wie ein Kreisdiagramm und funktioniert besser, ohne den Anteil jeder Gruppe irrezuführen.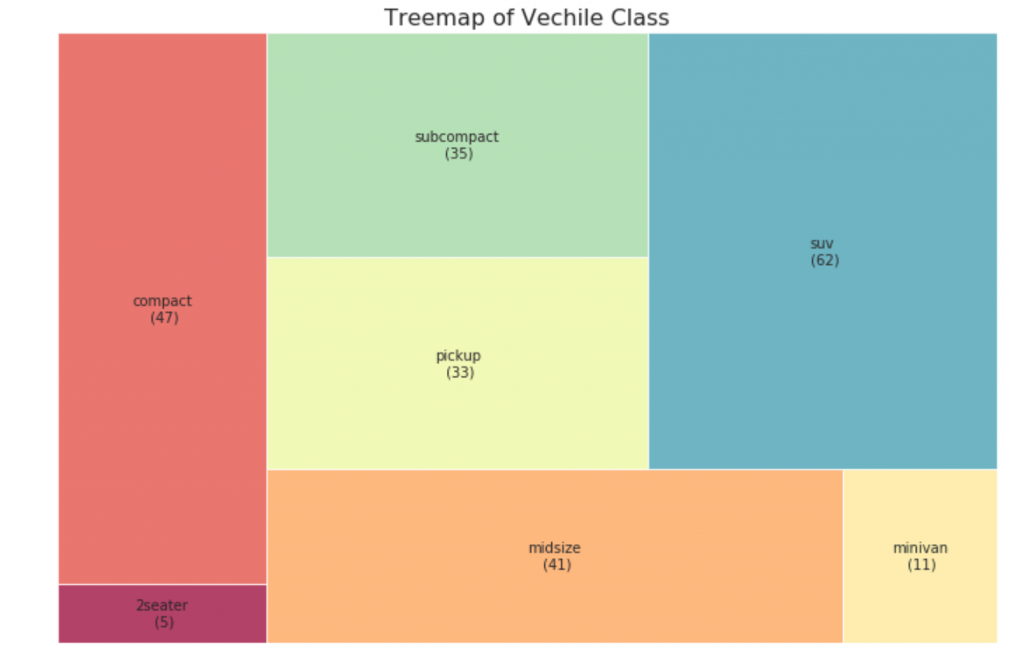
34. Histogramm
Ein Histogramm ist eine klassische Methode zur Visualisierung von Elementen basierend auf der Menge oder einer bestimmten Metrik. In der folgenden Abbildung habe ich für jedes Element unterschiedliche Farben verwendet. Sie können jedoch für alle Elemente eine Farbe auswählen, wenn Sie sie nicht in Gruppen einfärben möchten. Die Farbnamen werden in all_colors im folgenden Code gespeichert. Sie können die Farbe der Streifen ändern, indem Sie den Farbparameter in .plt.plot () festlegen.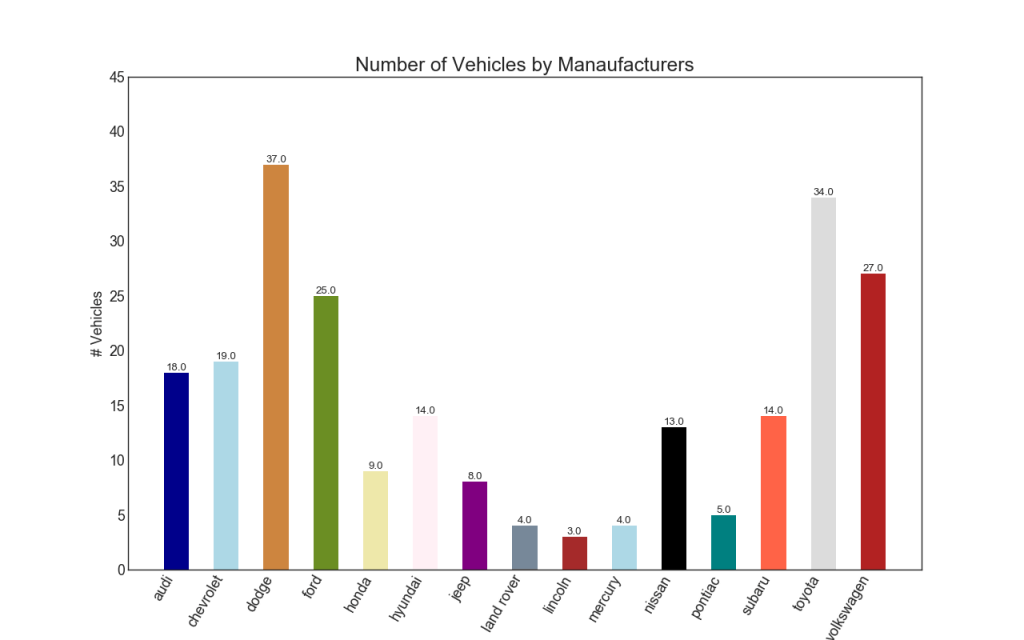
Tracking ändern
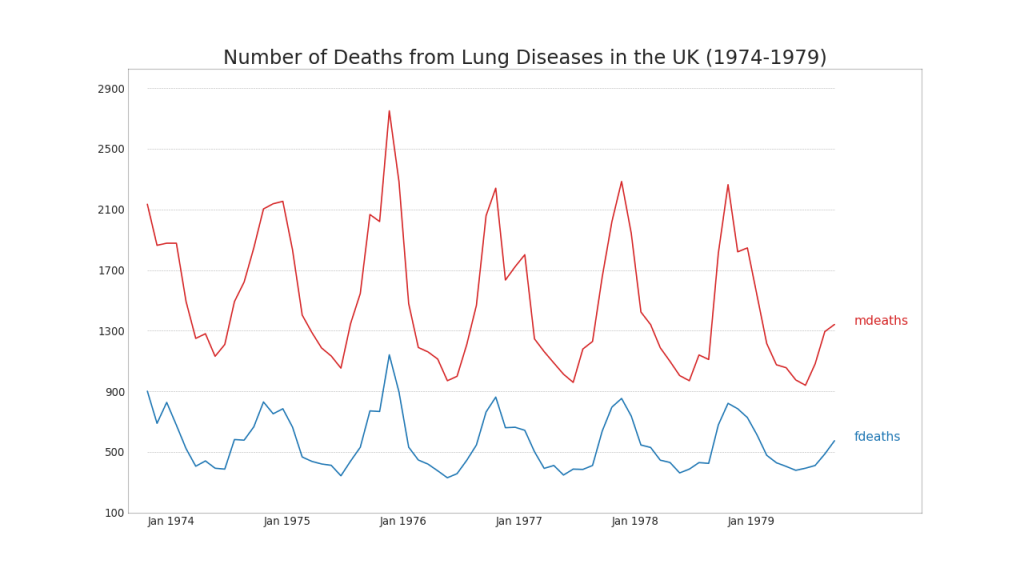
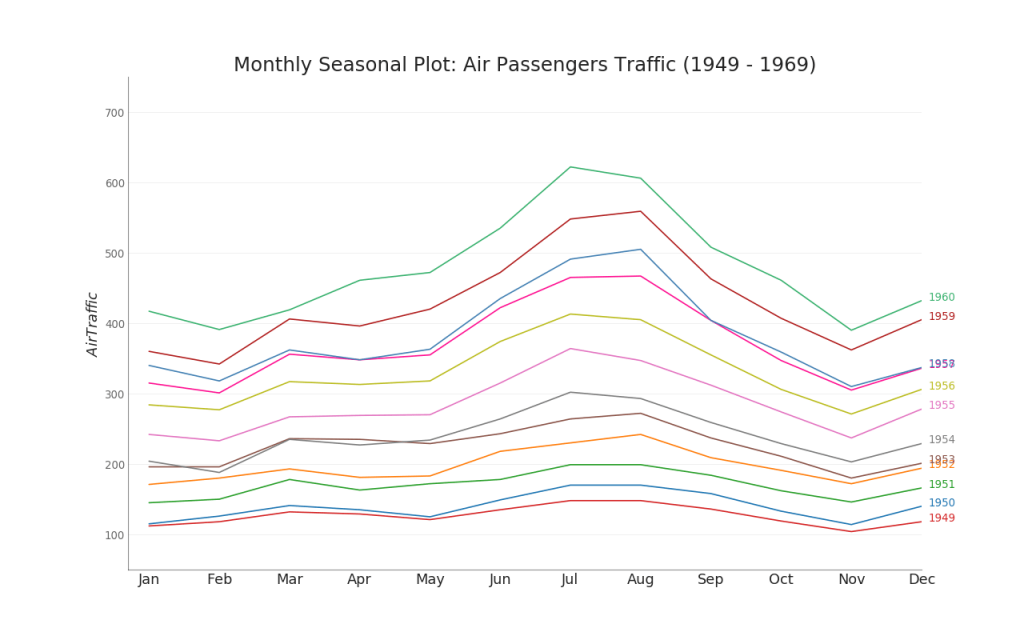
35. Zeitreihendiagramm
Ein Zeitreihendiagramm wird verwendet, um zu visualisieren, wie sich ein bestimmter Indikator im Laufe der Zeit ändert. Hier können Sie sehen, wie sich der Passagierstrom von 1949 bis 1969 verändert hat.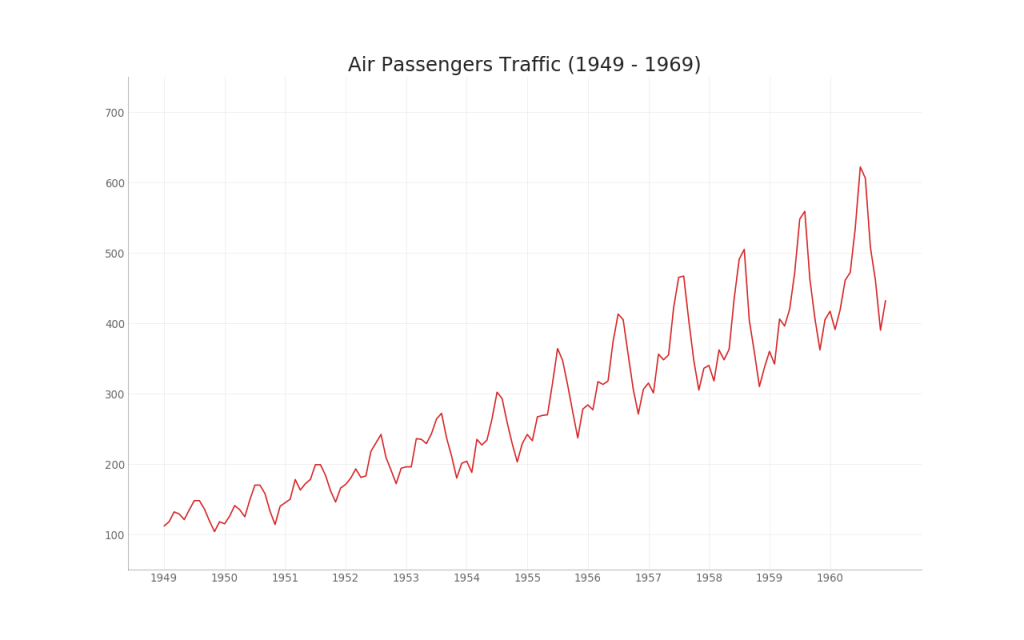
36. Zeitreihen mit Spitzen und Tälern
Die folgende Zeitreihe zeigt alle Spitzen und Täler an und markiert das Auftreten einzelner Sonderereignisse.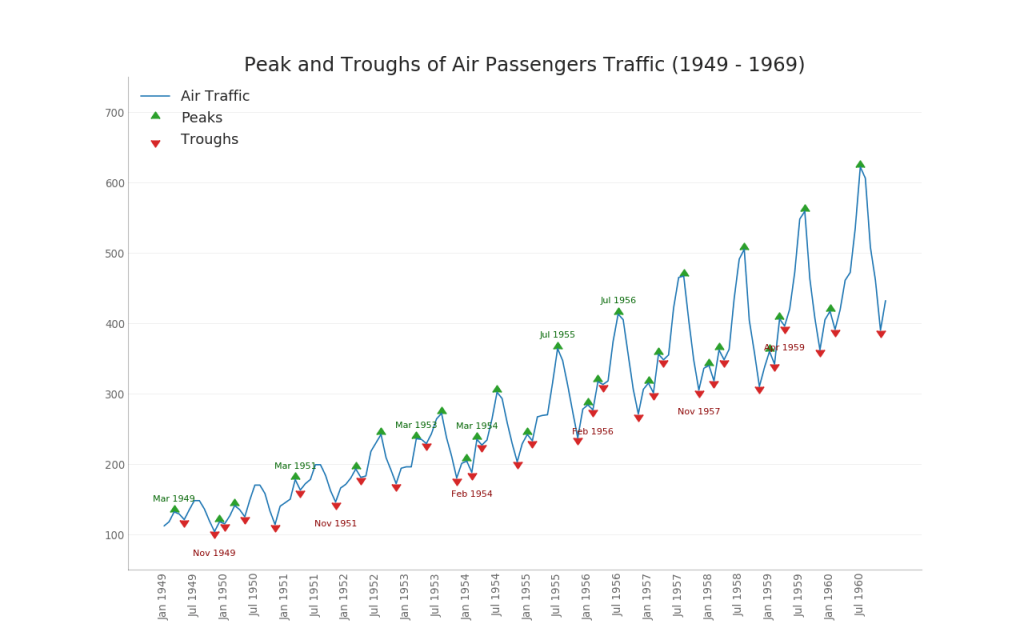
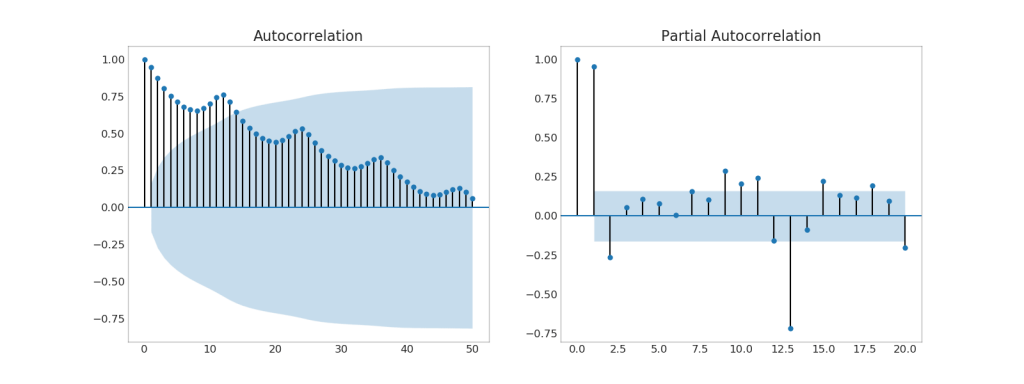
37. (ACF) (PACF)
Das ACF-Diagramm zeigt die Korrelation einer Zeitreihe mit ihrer eigenen Zeit. Jede vertikale Linie (im Autokorrelationsdiagramm) stellt eine Korrelation zwischen der Reihe und ihrer Zeit dar, beginnend zum Zeitpunkt 0. Der blau schattierte Bereich im Diagramm ist ein Signifikanzniveau. Die Momente, die über der blauen Linie liegen, sind von Bedeutung.Wie interpretieren Sie das?Für AirPassenger sehen wir, dass bei x = 14 die „Lutscher“ die blaue Linie überschritten haben und daher von großer Bedeutung sind. Dies bedeutet, dass der vor bis zu 14 Jahren beobachtete Passagierverkehr einen Einfluss auf den heute beobachteten Verkehr hat.PACF hingegen zeigt eine Autokorrelation einer bestimmten Zeit (Zeitreihe) mit der aktuellen Reihe, jedoch unter Beseitigung von Einflüssen zwischen ihnen.Code anzeigen from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
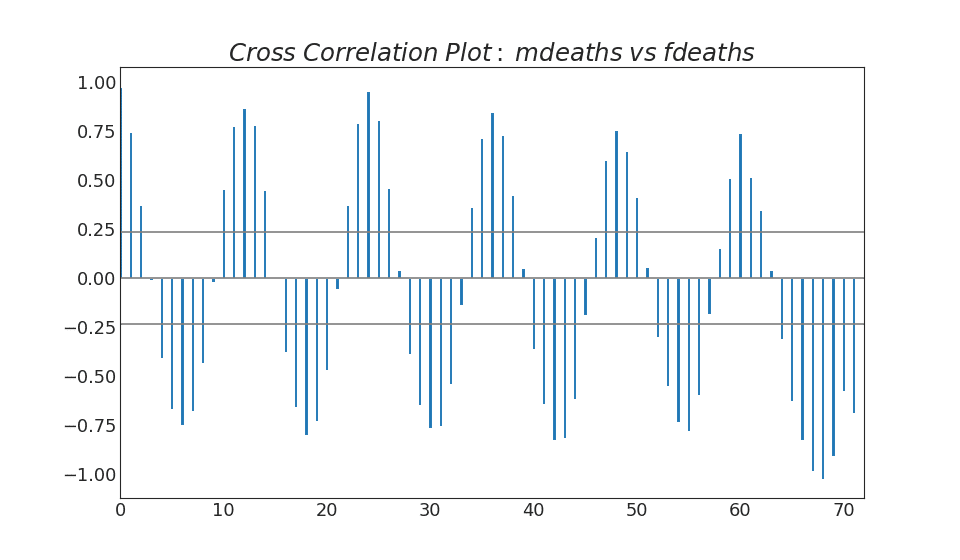
38. Kreuzkorrelationsgraph
.
import statsmodels.tsa.stattools as stattools
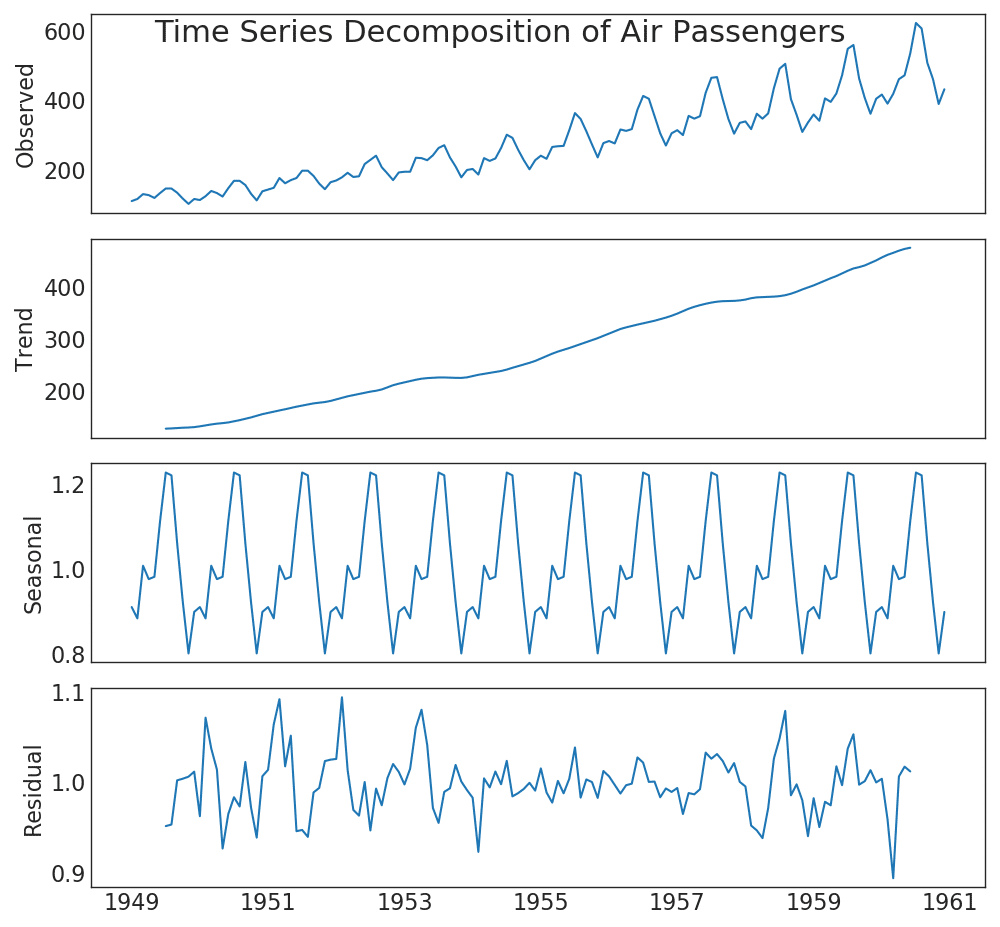
39.
, .
from statsmodels.tsa.seasonal import seasonal_decompose from dateutil.parser import parse
40.
, , .
41. Y
, , Y .
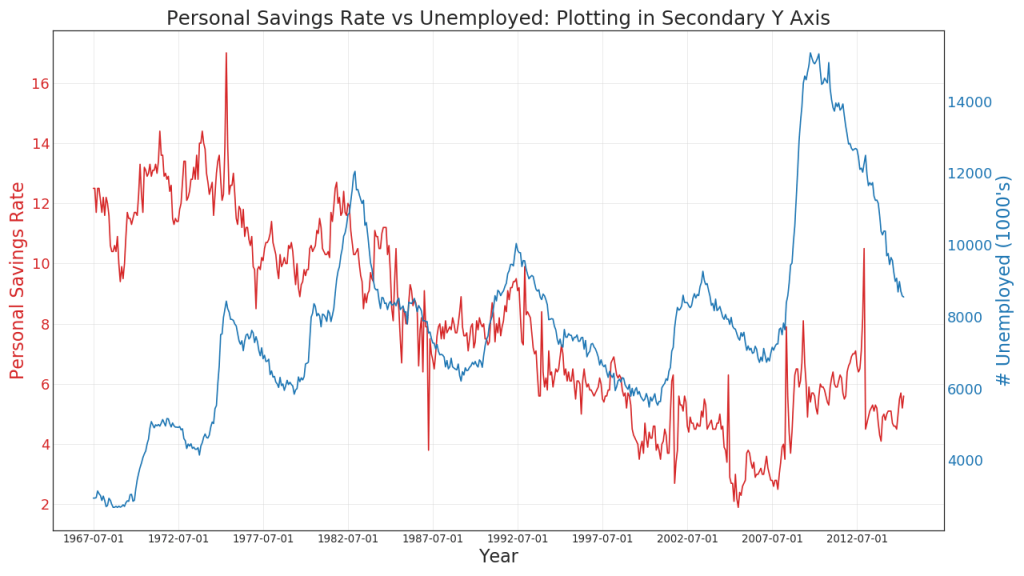
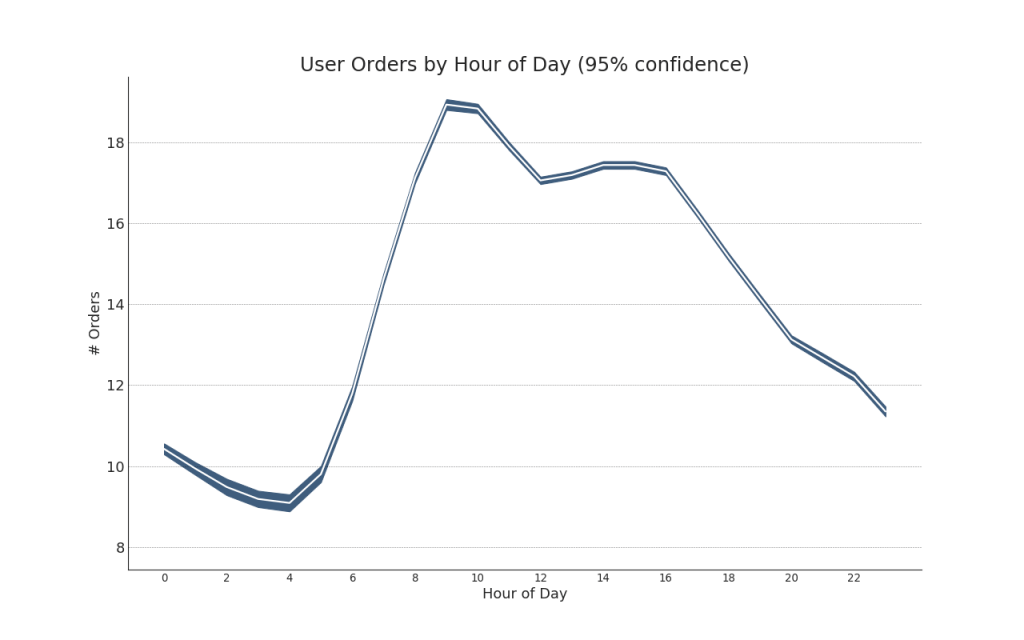
42.
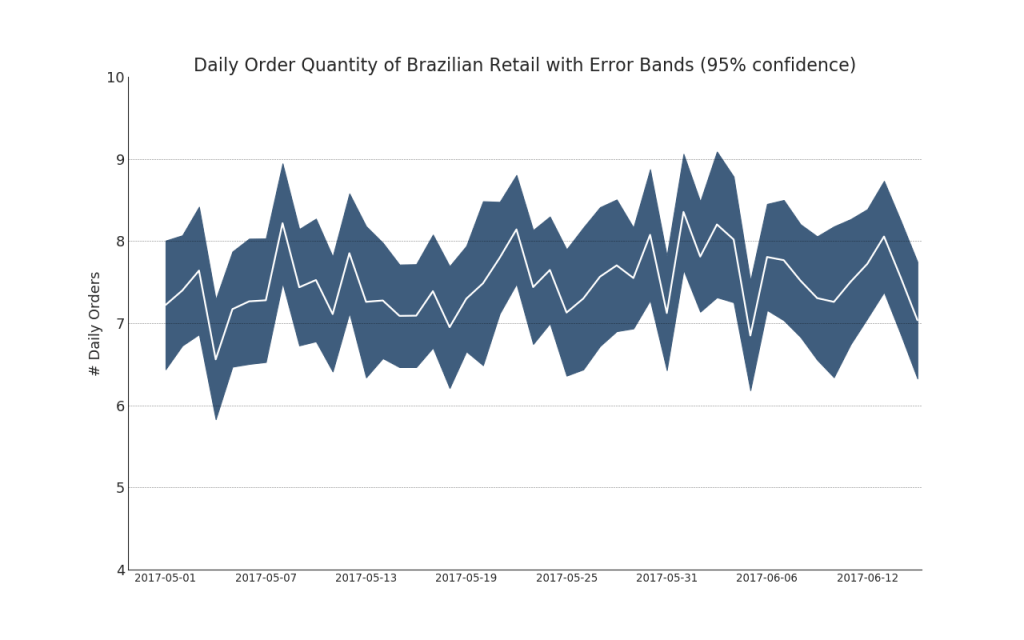
Zeitreihen mit Fehlerbalken können erstellt werden, wenn Sie einen Zeitreihendatensatz mit mehreren Beobachtungen für jeden Zeitpunkt (Datums- / Zeitstempel) haben. Unten sehen Sie einige Beispiele, die auf dem Eingang von Bestellungen zu verschiedenen Tageszeiten basieren. Und ein weiteres Beispiel für die Anzahl der Bestellungen, die innerhalb von 45 Tagen eingehen.Bei diesem Ansatz wird die durchschnittliche Anzahl der Bestellungen durch eine weiße Linie angezeigt. Und 95% -Intervalle werden berechnet und um den Durchschnitt herum aufgetragen.Code anzeigen from scipy.stats import sem
Code anzeigen "Data Source: https://www.kaggle.com/olistbr/brazilian-ecommerce#olist_orders_dataset.csv" from dateutil.parser import parse from scipy.stats import sem
43. Diagramm mit Akkumulation
Das gestapelte Flächendiagramm bietet eine visuelle Darstellung des Beitragssatzes aus mehreren Zeitreihen.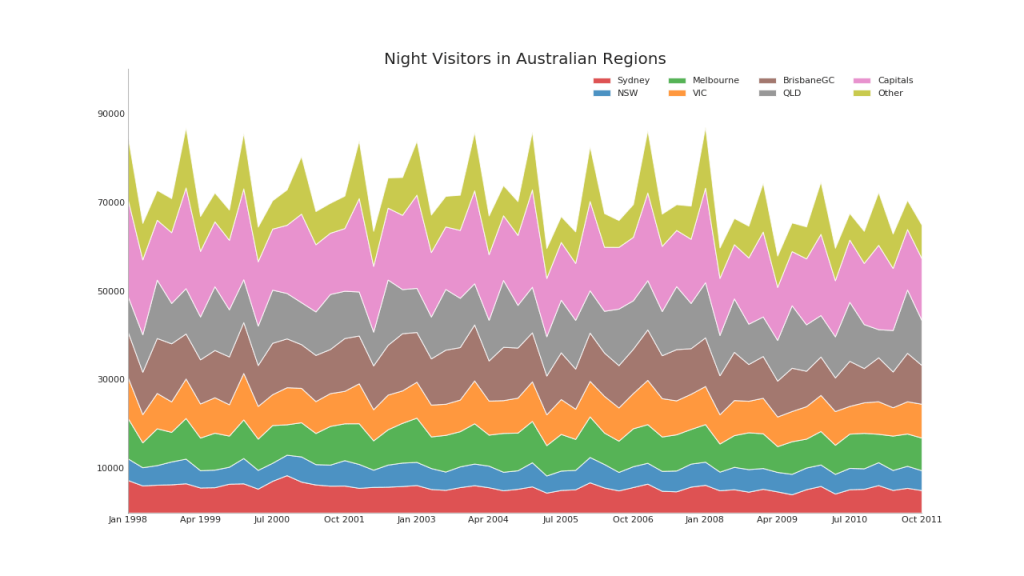
44. Flächendiagramm Nicht gestapelt
( ) . , . .
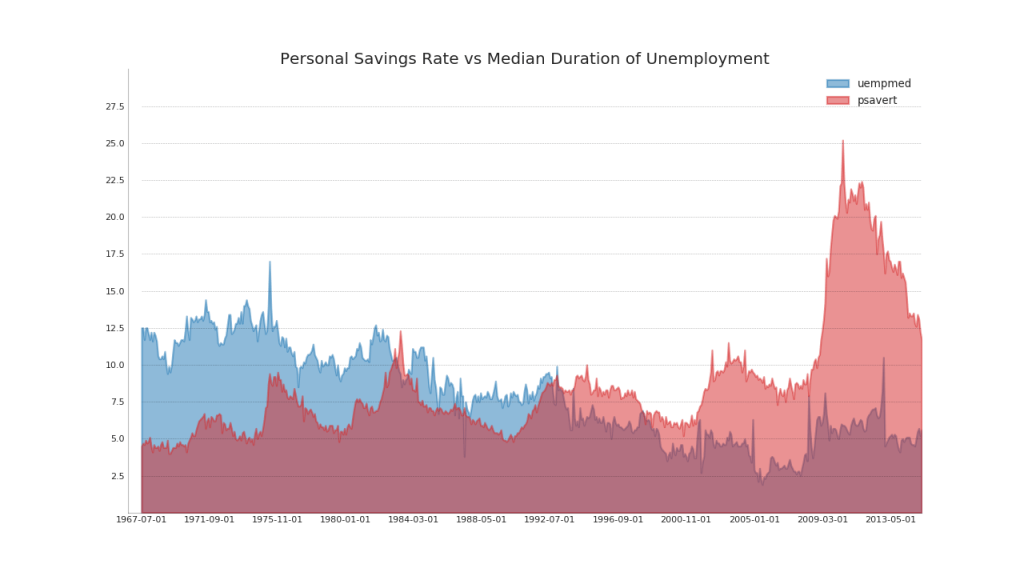
45.
. , .
import matplotlib as mpl import calmap

46.
, ( / / . .).
from dateutil.parser import parse
Gruppen
47.
.
import scipy.cluster.hierarchy as shc
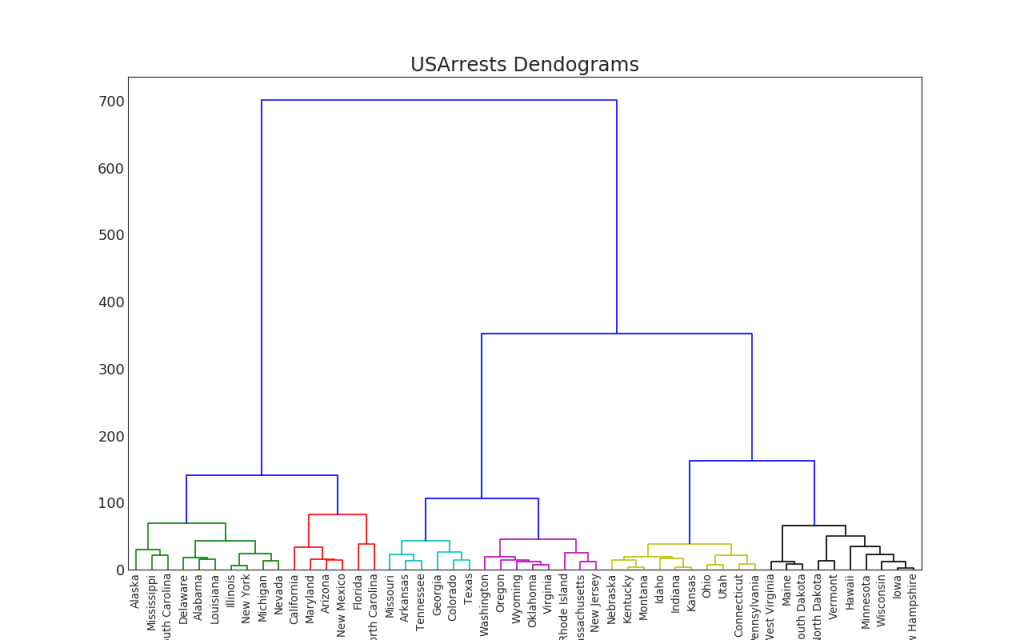
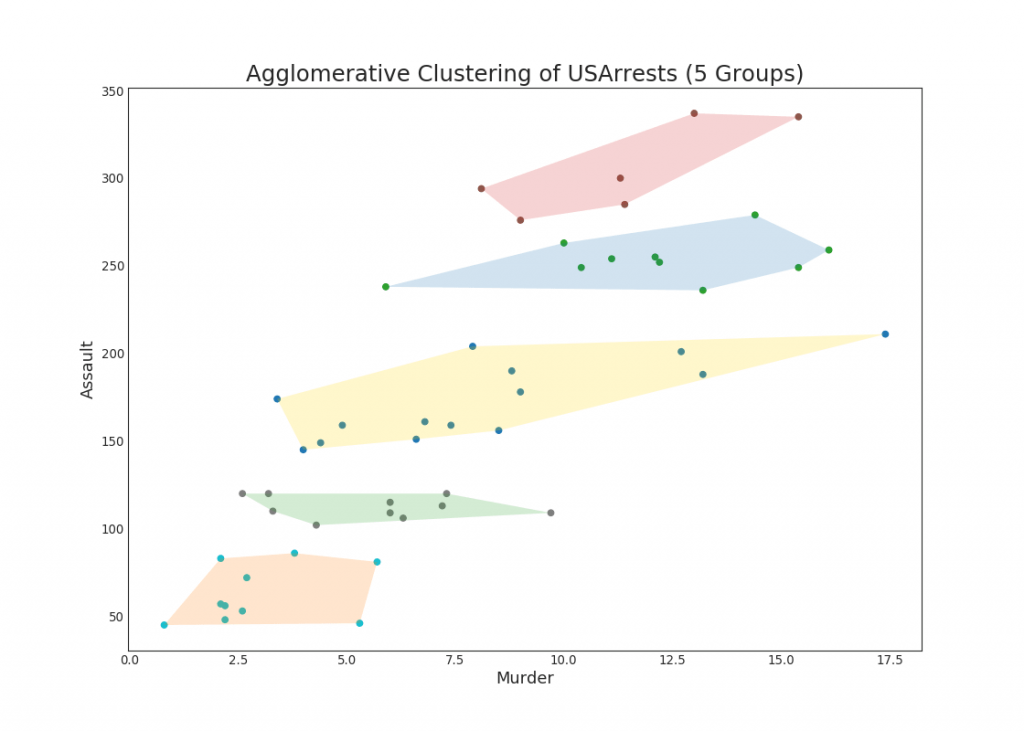
48.
, . 5 USArrests. «» «» X Y. X Y.
from sklearn.cluster import AgglomerativeClustering from scipy.spatial import ConvexHull
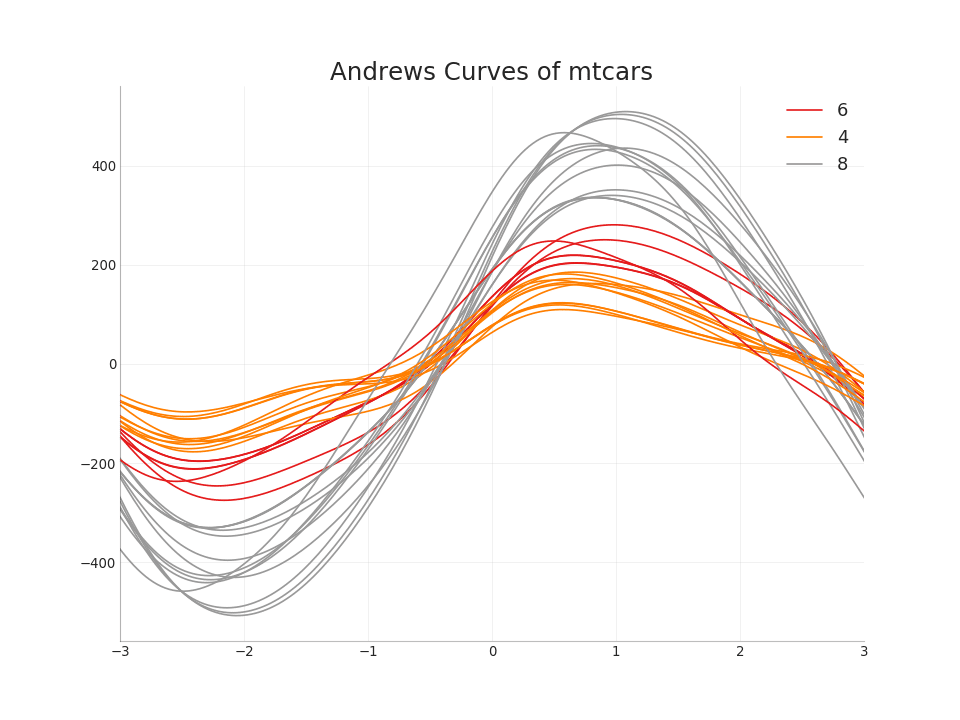
49.
, , . ( ) , ,
from pandas.plotting import andrews_curves
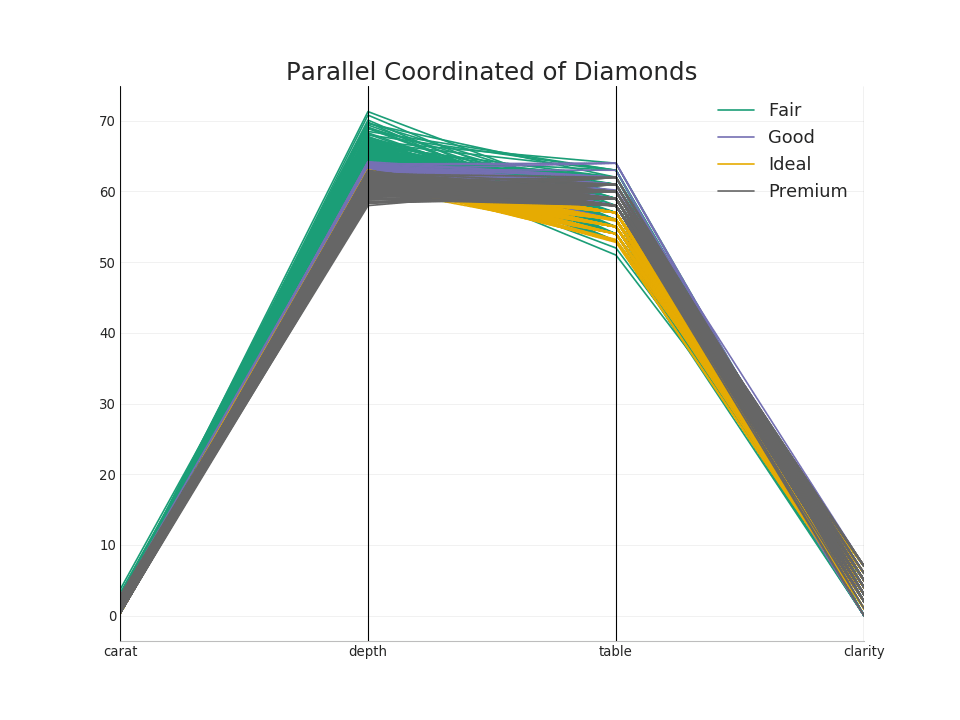
50. Parallele Koordinaten
Parallele Koordinaten helfen bei der Veranschaulichung, ob eine Funktion dazu beiträgt, Gruppen effektiv zu trennen. Wenn eine Trennung auftritt, ist diese Funktion wahrscheinlich sehr nützlich, um diese Gruppe vorherzusagen.Code anzeigen from pandas.plotting import parallel_coordinates
 Bonuscode in Jupiter
Bonuscode in JupiterGans, du hast Vibes versprochen!