Zurück in die Zukunft? Ausstehendes Radiergummi-Quantum

Artikel und Kommentare zu den Wundern der Quantenphysik erscheinen regelmäßig auf Habré: Quantenradierer und schwache Messungen. Leider werden sie zu oft als mysteriöse und unverständliche Phänomene bezeichnet, die es ermöglichen, fast Magie zu erschaffen, obwohl sie in Wirklichkeit absolut nichts Überraschendes enthalten. In diesem Beitrag übersetze ich Sean Carrolls Artikel über verzögerte Quantenlöscher. Lassen Sie es den Ausgangspunkt für die Diskussion in den Kommentaren aller Tricks der Quantenmechanik sein.

Vom Übersetzer. Sean Carroll ist Professor an der Caltech und auf Kosmologie und die Grundlagen der Quantenphysik spezialisiert. Er ist ein konsequenter Befürworter der Many-Worlds Interpretation (MMI) der Quantenmechanik, über die Something Deeply Hidden kürzlich veröffentlicht wurde. Dementsprechend wird die Erklärung des Experiments in der Post vom Standpunkt des MMI aus erfolgen. Obwohl dies im Großen und Ganzen für die Erklärung selbst nicht so wichtig ist. Sie können meinen letzten Beitrag über MMI lesen, wenn Sie die Grundlagen aktualisieren möchten.

Carroll veranstaltet auch einen großartigen Mindscape- Podcast. Dieser Podcast erwies sich im letzten Jahr als fast das Hauptereignis meines intellektuellen Lebens, und ehrlich gesagt ist dies das Beste, was Sie aus diesem Beitrag herausholen können.

Haftungsausschluss! An einigen Stellen habe ich einen kleinen Text angepasst und der Klarheit halber ein wenig von mir hinzugefügt. Alle Fehler sind auf meinem Gewissen (und in PM hoffe ich).

Dieser Artikel ist ein Kapitel aus Something Deeply Hidden , das in der endgültigen Version des Textes nicht enthalten war.



Stellen wir uns vor, Sie sind ein Physikstudent, der an einem Kurs in experimenteller Arbeit teilnimmt, und der Professor ist besonders schlecht gelaunt. Es zwingt Sie dazu, eine besonders seltsame Version von Jungs Erfahrung durchzuführen, und erklärt, dass diese Version als "Quantenlöscher mit verzögerter Auswahl" bezeichnet wird. Du scheinst so etwas schon einmal auf YouTube gesehen zu haben.
In Jungs traditionellem Experiment mit zwei Schlitzen passiert ein Elektronenstrahl zwei Schlitze und tritt in den Aufzeichnungsbildschirm ein. Jedes Elektron hinterlässt einzeln einen Punkt auf dem Bildschirm. Wenn wir jedoch warten, bis viele solcher Ereignisse eingegeben wurden, sehen wir ein Interferenzbild mit hellen und dunklen Streifen. Dies liegt daran, dass die Wellenfunktion der Elektronen beide Schlitze durchläuft und sich selbst stört.


Wenn wir messen, durch welche Lücke jedes Elektron geht, verschwindet das Interferenzbild und wir sehen eine geglättete Verteilung auf dem Bildschirm. Lehrbücher zur Quantenmechanik werden uns traditionell sagen, dass dies aufgrund des Zusammenbruchs der Wellenfunktion geschah, als wir sie an Schlitzen beobachteten. Die Multi-World-Interpretation besagt, dass dies darauf zurückzuführen ist, dass das Elektron das Messgerät und die Umgebung durcheinander gebracht hat (Dekohärenz aufgetreten) und die Wellenfunktion in zwei getrennte Welten unterteilt wurde, in denen das Elektron jeweils nur einen der Schlitze durchlief.

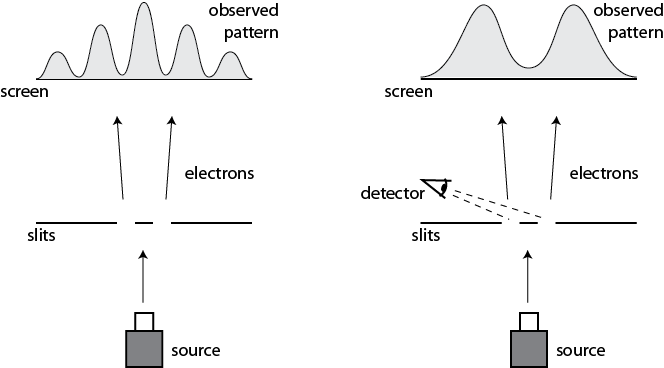Das Interferenzbild ist sichtbar, wenn das Elektron zwei Schlitze (links) passiert, bis versucht wird zu messen, durch welchen Schlitz das Elektron (rechts) geht.

Ihr Experiment ist kompliziert: Sie messen, durch welche Lücke ein Elektron geht, jedoch nicht mit einem großen makroskopischen Gerät, sondern mit einem Quantengerät, und speichern Informationen in einem Qubit. Zum Beispiel haben wir für jedes "Haupt" -Elektron, das durch die Lücken geht, ein zweites "Hilfs" -Elektron, das mit dem ersten verwickelt ist. Das Paar ist wie folgt verwirrt: Wenn das Hauptelektron durch die linke Lücke geht, befindet sich das Hilfselektron in einem Zustand mit Spin-up und wenn durch das rechte - mit Spin-down:

Ψ = (L) [↑] + (R) [↓].

Ihr Professor, der heute offensichtlich nicht in der Stimmung ist, besteht darauf, dass Sie keine Messungen an den "Hilfselektronen" vornehmen und sie nicht einmal wegfliegen lassen und gegen etwas im Raum stoßen. Sie fangen sie sorgfältig auf und lagern sie beispielsweise in einer Magnetfalle.
Was sehen wir auf dem Bildschirm, wenn wir ein solches Experiment mit vielen Elektronen wiederholen? Natürlich eine gleichmäßige Verteilung ohne Interferenzbild. Interferenzen können nur auftreten, wenn zwei Teile Komponenten derselben Wellenfunktion sind, und da zwei Hauptelektronen jetzt mit Hilfselektronen verschränkt sind, sind die Pfade durch den linken und rechten Schlitz unterscheidbar, und wir sehen das Interferenzbild nicht. In diesem Fall stellt sich heraus, dass es uns gleichgültig ist, dass wir keine wirkliche Dimension (und Dekohärenz) hatten, sondern nur Verwirrung. Wichtig ist nur, dass sich die Hauptelektronen in einem Zustand der Verschränkung mit Hilfselektronen befinden. Jede Verwirrung tötet Störungen.

Natürlich können wir die Spins von Hilfselektronen messen, wenn wir wollen. Wenn wir sie entlang der vertikalen Achse messen, erhalten wir [↑] oder [↓]. In Bezug auf den Quantenzustand Ψ wird dies uns entweder in das Universum bringen, in dem das Hauptelektron die linke Lücke passiert hat, oder in das Universum, in dem es die rechte Lücke passiert hat. Wenn wir das Experiment viele Male wiederholen, werden wir schließlich keine Interferenz sehen.

Okay, sagt Ihr Professor mit sadistischen Neigungen und reibt sich mit einem bösartigen Grinsen die Hände. Messen wir nun unsere Hilfselektronen, aber nicht auf der vertikalen, sondern auf der horizontalen Achse. Der Zustand in der vertikalen und horizontalen Basis hängt zusammen mit:
[↑] = [→] + [←],
[↓] = [→] - [←].

(Der Einfachheit halber verwerfen wir die Normalisierungsfaktoren). Auf dieser Basis sieht derselbe Zustand wie oben folgendermaßen aus:

Ψ = (L) [→] + (L) [←] + (P) [→] - (P) [←]
= ( + ) [→] + ( - ) [←].

Als wir den Hilfsspin in vertikaler Richtung gemessen haben, haben wir einen bestimmten Pfad des Hauptelektronens erhalten: [↑] war mit () verwickelt, und [↓] war mit () verwickelt. Bei einer Messung haben wir herausgefunden, ob das Hauptelektron durch den linken oder rechten Schlitz gelangt ist. Jetzt messen wir den Spin entlang der horizontalen Richtung und diese Gewissheit verschwindet. Nach der Messung befinden wir uns wieder im Zweig der Wellenfunktion, wo das Hauptelektron sofort zwei Schlitze passiert. Wenn wir den Spin „links“ messen, erhält das Hauptelektron eine Phasenverschiebung, wenn es durch den rechten Spalt (Minuszeichen) geht. Dies ist jedoch ein rein mathematisches Merkmal.
Bei dieser Messmethode haben wir also Informationen über die Lücke „gelöscht“, durch die das Elektron hindurchgegangen ist. Dies ist der sogenannte "Quantenlöscher". Der Löschvorgang selbst ändert nichts an der Gesamtverteilung der Punkte auf dem Bildschirm. Es bleibt glatt und es treten keine Störungen auf: Die Messergebnisse „links“ und „rechts“ sind immer noch zufällig.

Aber jetzt haben wir nicht nur die allgemeine Verteilung der Elektronen auf dem Bildschirm. Für jeden Punkt auf dem Bildschirm kennen wir auch das Messergebnis für das Hilfselektron: Es befand sich im Zustand „Spin nach links“ oder „Spin nach rechts“. Also, Ihr Professor blüht, gehen wir jetzt zum Computer und teilen unsere Messungen in zwei Teile: den Teil, für den das Hilfselektron links einen Spin hatte, und den Teil, für den es rechts war. Was werden wir jetzt sehen?

Es ist merkwürdig, dass jetzt wieder Störungen auftreten. Die Hauptelektronen, die den Hilfselektronen mit dem linken Spin zugeordnet sind, bilden ein Interferenzbild, ebenso wie diejenigen, für die das Hilfselektron einen Spin nach rechts hatte. (Denken Sie daran, dass das Interferenzbild nicht sofort angezeigt wird, sondern als Einzelelektronenstatistik erfasst wird.) Diese beiden Bilder sind jedoch relativ zueinander verschoben, so dass die Spitzen in einem Bild mit den Einbrüchen in dem anderen übereinstimmen. Wenn sie einander überlagert werden, tritt eine gleichmäßige Verteilung auf, bei der das Interferenzbild tatsächlich verborgen ist.

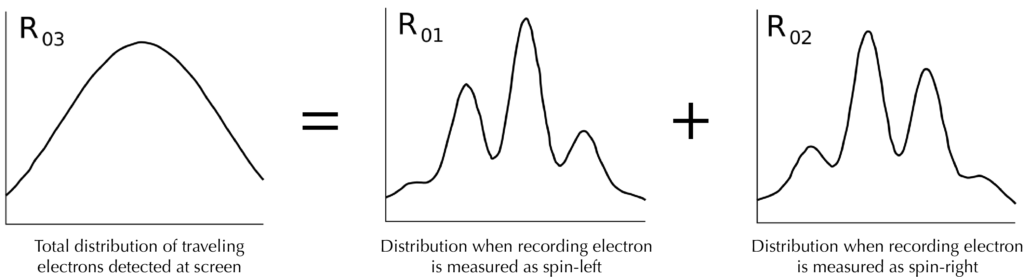
Entnommen aus Wikipedia

Rückblickend werden wir es nicht so überraschend finden. Wenn wir uns ansehen, wie der Zustand Ψ relativ zu den Hilfselektronen auf horizontaler Basis aufgezeichnet wurde (links oder rechts drehen), werden wir sehen, dass jede Messung mit dem Hauptelektronen verwickelt war, das durch beide Schlitze ging. Es können also natürlich Störungen auftreten. Und dieses Minus, das ein völlig unwichtiges mathematisches Detail zu sein schien, verschob ein Bild relativ zu einem anderen, so dass sie bei Überlagerung ein glattes Bild bildeten.

Ihr Professor scheint darüber mehr überrascht zu sein als Sie. "Kannst du nicht sehen!" Ruft sie aufgeregt aus. „Wenn wir überhaupt keine Hilfselektronen messen oder sie entlang der vertikalen Achse messen, entsteht keine Interferenz. Und wenn wir sie entlang der horizontalen Achse messen, stellt sich heraus, dass es eine versteckte Interferenz gab, die wir erkennen konnten, indem wir die Messergebnisse in Teile für verschiedene Spins des Hilfselektronens aufteilten. “

Sie und andere Schüler nicken zustimmend, obwohl Sie etwas ratlos sind.

„Denk darüber nach, was das bedeutet! Die Wahl der Messrichtung der Hilfsspins konnte getroffen werden, nachdem alle Hauptelektronen auf dem Bildschirm registriert wurden. Wenn wir alle Hilfsrücken retten würden, ohne sie mit der Umgebung verwechseln zu lassen, könnten wir diese Wahl Jahre später treffen. “

Es scheint ja, das Publikum murmelt, es scheint wahr zu sein.

„Interferenzen treten jedoch nur auf, wenn die Hauptelektronen beide Schlitze passieren, und eine gleichmäßige Verteilung tritt auf, wenn ein Elektron einen Spalt passiert. Diese Entscheidung - zwei Schlitze oder einen zu passieren - trifft lange bevor wir die Hilfselektronen gemessen haben. Unsere Entscheidung, sie eher horizontal als vertikal zu messen, hat natürlich ein Signal in die Vergangenheit zurückgesendet und die Haupthelektronen darüber informiert, dass sie beide Schlitze gleichzeitig und nicht einen durchlaufen müssen. “

Das verwirrte Publikum friert für einen Moment ein und explodiert aus Protest. Lösung? Zurück in die Vergangenheit? Worüber sprichst du? Das Elektron trifft nicht die Wahl, durch die eine oder andere Lücke zu gehen. Seine Wellenfunktion (und alles, womit es verwechselt wird) entwickelt sich wie üblich gemäß der Schrödinger-Gleichung. Ein Elektron trifft keine Wahl, es passiert definitiv immer beide Schlitze, aber es stellt sich heraus, dass es sich in einem verwirrten Zustand befindet. Durch Messen von Hilfselektronen in verschiedenen Richtungen können wir verschiedene Teile der verschränkten Wellenfunktion auswählen, von denen einige interferieren und andere nicht. Nichts ist in die Vergangenheit zurückgekehrt. Dies ist ein cooles Experiment, aber hier baut niemand eine Zeitmaschine.

Sie und Ihre Kameraden haben recht. Ihr Professor ist ein wenig mitgerissen. Es besteht immer die Versuchung, sich das Elektron als etwas vorzustellen, das „gleichzeitig die Eigenschaften einer Welle und eines Teilchens besitzt“, und die Kopenhagener Interpretation der Quantenmechanik duldet dies nur. Wenn wir dieser Versuchung erliegen, ist die Vorstellung, dass sich das Elektron entweder als Teilchen oder als Welle verhält und in jedem Experiment eine dieser beiden Optionen verwirklicht wird, nicht weit entfernt. Und von dieser Position aus führt ein Quantenlöscher mit einer verzögerten Auswahl tatsächlich zu dem Schluss, dass die Informationen in die Vergangenheit zurückübertragen werden sollten, um dem Elektron bei der Auswahl zu helfen. Ehrlich gesagt erschweren populäre Erklärungen oft das Bild und erzeugen eine Aura des Geheimnisses in der Quantenmechanik. Und die Annahme, dass die Quantenmechanik es Ihnen ermöglicht, Signale in die Vergangenheit zu senden, fügt dem Feuer nur Treibstoff hinzu.

All diesen Versuchungen muss widerstanden werden. Ein Elektron ist einfach Teil der Wellenfunktion des Universums. Er trifft nicht die Wahl, ein Teilchen oder eine Welle zu sein. Aber aus irgendeinem Grund betrachten selbst ernsthafte Forscher der Grundlagen der Quantenphysik manchmal Experimente mit einem Quantenradierer mit verzögerter Wahl und ähnlichen (die übrigens in der Praxis viele Male getestet wurden) als Beweis für die umgekehrte Kausalität in der Natur - Signale, die sich zeitlich rückwärts ausbreiten. die Vergangenheit beeinflussen. Eine Variante eines solchen Experiments, die von keinem anderen als John Wheeler vorgeschlagen wurde, schlug mehrere Teleskope auf der anderen Seite des Bildschirms vor, die bestimmen konnten, durch welche Lücke das Elektron ging, viel später als in dem Moment, in dem es passierte. Im Gegensatz zu späteren Kommentatoren ging Wheeler nicht so weit, eine umgekehrte Kausalität vorzuschlagen, und bestand nicht darauf, dass das Elektron immer entweder ein Teilchen oder eine Welle ist.

Es ist keine umgekehrte Kausalität erforderlich, um einen verzögerten Quantenlöscher zu erklären. Für den Anhänger einer Multi-Welt-Interpretation ist das Ergebnis ohne Zeitreise offensichtlich. Der Trick besteht darin, dass das Elektron, wenn es mit einem Dreh verwickelt ist und nicht mit einem großen Teilchenensemble in einem klassischen Detektor und einer klassischen Umgebung, nicht im vollen Sinne des Wortes entkoppelt. Wenn das Hauptelektron nur mit einem Teilchen verwickelt ist, können wir verschiedene Optionen zur Messung dieses Hilfsteilchens in Betracht ziehen. Wenn wir wie in Jungs üblichem Experiment die Lücke gemessen haben, durch die ein Elektron mit einem klassischen makroskopischen Gerät hindurchgegangen ist, haben wir keine solche Auswahl an Messoptionen. Mit wahrer Dekohärenz wird die winzige Größe der ursprünglichen Verschränkung im Wesentlichen irreversibel in eine Verstrickung mit der Umwelt verstärkt. In diesem Sinne erweist sich ein Quantenlöscher mit verzögerter Auswahl als nützliches Gedankenexperiment, um die Rolle von Dekohärenz und Umgebung bei Messungen zu erkennen.

Leider ist nicht jeder ein Befürworter einer Multi-Welt-Interpretation. In anderen Versionen der Quantenmechanik kollabieren Wellenfunktionen tatsächlich, im Gegensatz zur multivariaten Interpretation, bei der der Kollaps nur aufgrund der Dekohärenz erkennbar ist. In Interpretationen, in denen der Kollaps tatsächlich auftritt (wie z. B. GRW), stellt sich heraus, dass er zeitlich asymmetrisch ist: Die Wellenfunktionen kollabieren, können jedoch nicht in ihren ursprünglichen Zustand zurückkehren. Wenn in Ihrer Theorie die Wellenfunktion zusammenbricht, Sie aber gleichzeitig die allgemeine Zeitsymmetrie in den Gesetzen der Physik beibehalten möchten, können Sie sich von der Notwendigkeit einer umgekehrten Kausalität überzeugen.

Oder Sie können die reibungslose Entwicklung der Wellenfunktion eher mit Verzweigung als mit Kollaps akzeptieren und automatisch die Zeitsymmetrie für alle Grundgleichungen beibehalten, ohne Zeitreisen oder Zweifel an Elektronen.

Willkommen in den vielen Welten!