Hallo!
In diesem "Artikel" oder besser gesagt dem Aufsatz werde ich einen sehr einfachen Weg zeigen, um Spaß daran zu haben, die Grundlagen von Latex und Python zu kennen.
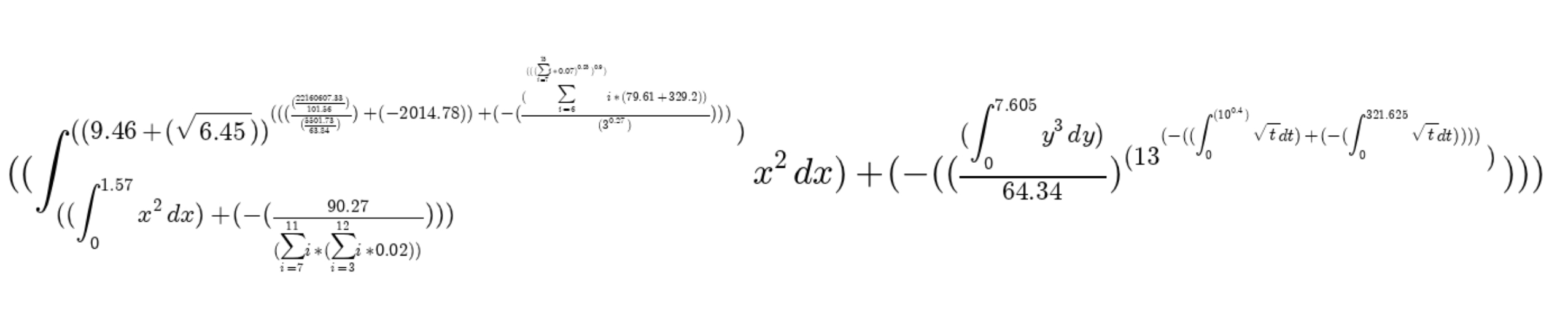
Warum?
Nun, Sie können einfache Ausdrücke generieren, die Kinder zählen können. Oder einfach so. Ja, zumindest die Tapete aufsetzen, wenn Sie so fanatisch sind wie ich.
Wie soll das funktionieren?
Die Idee ist wirklich sehr einfach, absolut jeder kann ein solches Programm schreiben. Wir wollen einen Ausdruck erzeugen, der einer Zahl n entspricht (die der Benutzer eingibt). Jede Zahl kann durch einen arithmetischen Ausdruck ersetzt werden, zum Beispiel 3 = 1 + 2. Und 2 ist 4 / 2. Auf diese Weise haben wir 3 = 1 + 4/2 generiert. In ähnlicher Weise führen wir verschiedene Operationen ein und verpacken sie in LaTeX, die Formelsprache.
Du wirst brauchen ...Eine Woche Erfahrung in Python und Matplotlib. Ich meine es ernst.
Hauptmechanismus
Wir müssen den Ausdruck analysieren, um die Zahlen herauszuholen. Nennen wir unsere Klasse einen Generator von Problemen (wir alle vermissen es so sehr!)
import random from math import log import math import sys sys.setrecursionlimit(1000)
Die Funktion extract_nums bedeutet, n Zahlenpaare (a, b) zu erhalten, wobei a die Position des ersten Zeichens und b die Position des letzten + 1 ist.
Zum Beispiel, wenn wir den folgenden Code ausführen:
gen = ProblemGenerator() print(gen.extract_nums("13+256/355+25"))
Wir werden sehen:
[(0, 2), (3, 6), (7, 10), (11, 13)]
Das heißt, es ist ein Tupel-Array. (0, 2) bedeutet, dass es eine Zahl zwischen 0 (einschließlich) und 2 (nicht einschließlich) gibt.
Nun möchten wir verschiedene Operatoren erstellen. Beginnen wir mit Multiplikation und Summe. Deklarieren Sie drei Funktionen
def unmin(*args, acc=2): r = [] for arg in args: f = round(arg, acc) if f > 0: f = str(f) else: f = "(" + str(f) + ")" r.append(f) return r def __c_sum(num): a = round(random.random() * 100, 3) b = num - a a, b = unmin(a, b) return a + " + " + b def __c_mul(num): a = num / (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = num / a a, b = unmin(a, b) return a + " * " + b
Die Unmin-Funktion besteht nicht nur darin, alle Argumente einfach in Zeichenfolgen zu konvertieren, sondern auch einen Operanden in Klammern zu setzen, wenn er kleiner als Null ist. Zum Beispiel haben wir die Zahlen a = 3, b = -4. Wenn wir schreiben
a = 3 b = -4 a, b = unmin(a, b)
Dann ist a = "3", b = "(- 4)"
Nun, der Rest der Funktionen ist klar: __c_sum gibt eine Zeichenfolge der Form "13 + 4" und __c_mul "13 * 4" zurück.
Es bleibt, diese beiden Teile zu kombinieren und jede Zahl im Ausdruck durch den Ausdruck zu ersetzen.
Fügen Sie ProblemGenerator den folgenden Code hinzu:
class ProblemGenerator: ... def __init__(self): self.funcs = [] def add_expander(self, func): self.funcs.append(func) def complexify(self, num): return random.choice(self.funcs)(num) def __rxp__(self, exp): x, y = random.choice(self.extract_nums(exp)) exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:] return exp def randexpr(self, ans, steps): e = str(ans) for i in range(steps): e = self.__rxp__(e) return e
complexify nimmt eine Zahl und gibt eine Zeichenfolge zurück - ein komplizierter Ausdruck. Zum Beispiel, wenn wir schreiben:
gen = ProblemGenerator() gen.add_expander(__c_sum) print(gen.complexify(13))
Wir bekommen:
31.2 + (-18.2)
Wie funktioniert __rxp__? Wir wählen zufällig die Position einer Zahl aus einem Ausdruck aus (wenn es beispielsweise einen Ausdruck „13 + 35/45“ gibt, nehmen wir an, wir haben (3, 5) ausgewählt) und ersetzen diese Zahl durch einen Ausdruck, der dieser Zahl entspricht. Das heißt, ich möchte:
"13 + 35/45" - eine Zufallszahl (3, 5)
13+ + (12 + 23) + / 45
13+ (12 + 23) / 45
So funktioniert __rxp__
Nun, randexpr funktioniert ganz einfach. Wenn wir beispielsweise vier Schritte haben, wird der Ausdruck folgendermaßen geöffnet:
13 (5.62 + 7.38) ((20.63 + (-15.01)) + 7.38) ((20.63 + (-(67.5 + (-52.49)))) + 7.38) ((20.63 + (-((15.16 + 52.34) + (-52.49)))) + 7.38)
Versuchen wir zu rennen:
gen = ProblemGenerator() gen.add_expander(__c_sum) gen.add_expander(__c_mul) exp = gen.randexpr(1, 5) print(exp)
Ergebnis:
((6.63 + (56.62 + 16.8)) + (-((60.53 + 3.61) + 14.91)))
LaTeX
Seltsamerweise bleibt das Einfachste. Wir werden eine Reihe verschiedener LaTeX-Betreiber bekannt geben:
def __l_sum(num): a = 100 ** (random.random() * 2) b = num - a a, b = unmin(a, b) return a + " + " + b def __l_div(num): a = num * (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = a / num a, b = unmin(a, b) return "\\frac{" + a + "}{" + b + "}" def __l_pow(num): if num == 0: return str(random.randint(2, 7)) + "^{-\\infty}" a = random.randint(0, 10) + 3 b = math.log(abs(num), a) a, b = unmin(a, b) return ("-" if num < 0 else "") + a + "^{" + b + "}" def __l_sqrt(num): a = num ** 0.5 a = unmin(a)[0] return "\\sqrt{" + a + "}" def __l_int(num): patterns = [ ("x^{2}", (3 * num) ** (1/3), "dx"), ("y^{3}", (4 * num) ** (1/4), "dy"), ("\sqrt{t}", (1.5 * num) ** (2/3), "dt") ] p, b, f = random.choice(patterns) b = str(round(b, 3)) return "\\int_{0}^{" + b + "} " + p + " " + f def __l_sig(num): a = random.randint(1, 10) b = random.randint(1, 10) + a s = sum([i for i in range(a, b + 1)]) c = num / s a, b, c = unmin(a, b, c) return "\\sum_{i=" + a + "}^{" + b + "} i*" + c
Fügen Sie alle Funktionen zu gen hinzu:
gen = ProblemGenerator() gen.add_expander(__l_sum)
Fügen Sie abschließend die Ausgabe des Ergebnisses hinzu:
import matplotlib.pyplot as plt plt.axis("off") latex_expression = gen.randexpr(1, 30)
Das ist alles.
Ganzer Code import random from math import log import math import sys sys.setrecursionlimit(1000) class ProblemGenerator: def extract_nums(self, exp): symbols = list(exp) NUM = "1234567890." for i in range(len(symbols)): symbols[i] = "N" if symbols[i] in NUM else "T" begins = [] ends = [] for i in range(len(symbols) - 1): fn = symbols[i] + symbols[i + 1] if fn == "TN": begins.append(i) elif fn == "NT": ends.append(i) if exp[-1] in NUM: ends.append(len(exp) - 1) if exp[0] in NUM: begins = [-1] + begins return [(x + 1, y + 1) for x, y in zip(begins, ends)] def __init__(self): self.funcs = [] def add_expander(self, func): self.funcs.append(func) def complexify(self, num): return random.choice(self.funcs)(num) def __rxp__(self, exp): x, y = random.choice(self.extract_nums(exp)) exp = exp[:x] + "(" + self.complexify(float(exp[x:y])) + ")" + exp[y:] return exp def randexpr(self, ans, steps): e = str(ans) for i in range(steps): e = self.__rxp__(e) return e def unmin(*args, acc=2): r = [] for arg in args: f = round(arg, acc) if f > 0: f = str(f) else: f = "(" + str(f) + ")" r.append(f) return r def __c_sum(num): a = round(random.random() * 100, 3) b = num - a a, b = unmin(a, b) return a + " + " + b def __c_mul(num): a = num / (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = num / a a, b = unmin(a, b, acc=5) return a + " * " + b def __c_sub(num): a = num + 100 ** (random.random() * 2) b = (a - num) a, b = unmin(a, b) return a + " - " + b def __c_log(num): fr = random.randint(300, 500) a = math.e ** (num / fr) a, fr = unmin(a, fr, acc=5) return "log(" + a + ") * " + fr def __l_sum(num): a = 100 ** (random.random() * 2) b = num - a a, b = unmin(a, b) return a + " + " + b def __l_div(num): a = num * (random.random() * 100 + 10) if a == 0.0: b = random.random() else: b = a / num a, b = unmin(a, b) return "\\frac{" + a + "}{" + b + "}" def __l_pow(num): if num == 0: return str(random.randint(2, 7)) + "^{-\\infty}" a = random.randint(0, 10) + 3 b = math.log(abs(num), a) a, b = unmin(a, b) return ("-" if num < 0 else "") + a + "^{" + b + "}" def __l_sqrt(num): a = num ** 0.5 a = unmin(a)[0] return "\\sqrt{" + a + "}" def __l_int(num): patterns = [ ("x^{2}", (3 * num) ** (1/3), "dx"), ("y^{3}", (4 * num) ** (1/4), "dy"), ("\sqrt{t}", (1.5 * num) ** (2/3), "dt") ] p, b, f = random.choice(patterns) b = str(round(b, 3)) return "\\int_{0}^{" + b + "} " + p + " " + f def __l_sig(num): a = random.randint(1, 10) b = random.randint(1, 10) + a s = sum([i for i in range(a, b + 1)]) c = num / s a, b, c = unmin(a, b, c) return "\\sum_{i=" + a + "}^{" + b + "} i*" + c gen = ProblemGenerator() gen.add_expander(__l_sum) gen.add_expander(__l_div) gen.add_expander(__l_pow) gen.add_expander(__l_sqrt) gen.add_expander(__l_int) gen.add_expander(__l_sig) import matplotlib.pyplot as plt plt.axis("off") latex_expression = gen.randexpr(1, 30)