Zwei Seiten reichten aus, um die 30-jährige Hypothese aus dem Bereich der Informatik zu belegen.

Die "Sensitivitäts" -Hypothese verwirrte viele prominente Informatiker, aber ihre neuen Beweise erwiesen sich als so einfach, dass ein Forscher sie auf einen einzigen Tweet reduzieren konnte

Die in diesem Sommer veröffentlichte Arbeit beendet die fast 30-jährige Geschichte der Hypothese bezüglich der Struktur der Grundbausteine ​​von Computerschaltungen. Diese Hypothese der „Sensibilität“ hat viele prominente Informatiker jahrelang verwirrt, aber ihre neuen Erkenntnisse erwiesen sich als so einfach, dass ein Forscher sie auf einen einzigen Tweet reduzieren konnte.

"Diese Hypothese war eine der nervigsten und beschämendsten offenen Aufgaben in allen Bereichen der Kombinatorik und theoretischen Informatik", schrieb Scott Aaronson von der University of Texas in Austin in seinem Blog. "Die Liste der Personen, die versucht haben, dies zu beweisen, und es nicht geschafft haben, ist eine Liste der bekanntesten Personen in der diskreten Mathematik und der theoretischen Informatik", fügte er in einer E-Mail hinzu.

Diese Hypothese ist mit Booleschen Funktionen verbunden - den Regeln zum Konvertieren von Zeichenfolgen eingehender Bits (Nullen und Einsen) in ein einzelnes Bit. Eine solche Regel erzeugt 1, wenn alle eingehenden Bits 1 sind, und andernfalls 0; Eine andere Regel gibt 0 zurück, wenn die Zeile eine gerade Anzahl von Einheiten enthält, und 1 in einem anderen Fall. Jede Computerschaltung ist eine Kombination von Booleschen Funktionen, was sie zum „Baumaterial für alles macht, was in der Informatik getan wird“, sagte Rocco Cenedio von der Columbia University.


Im Laufe der Jahre wurden in der Informatik viele Möglichkeiten entwickelt, um die Komplexität einer bestimmten Booleschen Funktion zu messen. Jede Messung verwendet ihren eigenen Aspekt, wie die Eingabezeileninformationen das Ausgabebit bestimmen. Zum Beispiel gibt die "Empfindlichkeit" einer Booleschen Funktion grob gesagt die Wahrscheinlichkeit an, dass das Ändern eines einzelnen Bits am Eingang das Bit am Ausgang ändert. Und "Anforderungskomplexität" berechnet, wie viele eingehende Bits angefordert werden müssen, um mit Sicherheit zu wissen, wie die ausgehenden sein werden.

Jede Kennzahl gibt einen eigenen Standpunkt zur Struktur einer Booleschen Funktion. Informatiker stellten jedoch fest, dass fast alle diese Maßnahmen in eine universelle Plattform passen und dass man anhand des Werts einer von ihnen die Bedeutung der anderen ungefähr beurteilen kann. Und nur ein Maß für die Komplexität passte nicht in dieses Schema: Sensibilität.

1992 schlugen Noam Nisan von der Hebrew University of Jerusalem und Mario Szeged, der jetzt an der Rutgers University arbeitet, vor, dass Sensibilität immer noch in diese Plattform passt. Aber niemand konnte es beweisen. "Ich würde sagen, diese Frage war im Bereich der Untersuchung boolescher Funktionen hervorragend", sagte Cenedio.

"Die Leute haben lange, komplexe Werke geschrieben und versucht, nur sehr geringe Fortschritte zu erzielen", sagte Ryan O'Donnell von der Carnegie Mellon University.

Und jetzt hat Hao Huang , ein Mathematiker der Emory University, die Sensitivitätshypothese mit Hilfe eines brillanten, aber elementaren zweiseitigen Beweises in Bezug auf die Kombinatorik von Punkten auf Würfeln bewiesen. "Es ist wunderschön wie eine kostbare Perle", schrieb Claire Matthew vom französischen staatlichen Zentrum für wissenschaftliche Forschung in einem Interview über Skype.

Aaronson und O'Donnell nannten das Werk von Juan "Buch" als Beweis für die Hypothese der Sensibilität und bezogen sich auf das Konzept des "himmlischen Buches" von Pal Erdös, in dem Gott ideale Beweise für jeden Satz aufschreibt. "Es fällt mir schwer, mir vorzustellen, dass selbst Gott einen einfacheren Beweis für den Sensitivitätssatz kennt", schrieb Aaronson.

Sensibles Thema

Stellen Sie sich vor, sagte Matthew, dass Sie ein Formular mit Fragen auf dem Antragsformular für Bankdarlehen ausfüllen, deren Antworten Ja / Nein sein können. Wenn Sie fertig sind, wertet der Bankier die Ergebnisse aus und teilt Ihnen mit, ob Sie für einen Kredit geeignet sind. Dieser Prozess ist eine boolesche Funktion: Ihre Antworten sind eingehende Bits, und die Entscheidung des Bankiers ist ausgehend.

Wenn Ihre Bewerbung abgelehnt wird, können Sie darüber nachdenken, ob Sie das Ergebnis ändern können, indem Sie in einer einzigen Frage liegen - vielleicht indem Sie angeben, dass Sie mehr als 50.000 USD pro Jahr verdienen, obwohl dies nicht der Fall ist. Wenn diese Lüge das Ergebnis der Betrachtung ändert, werden Informatiker eine solche Boolesche Funktion als "empfindlich" für den Wert eines bestimmten Bits bezeichnen. Wenn Sie beispielsweise an einer von sieben Stellen liegen und jedes Mal das Ergebnis ändern, beträgt die Sensitivität der Booleschen Funktion zur Bewertung Ihres Kreditantrags sieben.

Informatiker definieren die Gesamtsensitivität einer Booleschen Funktion als den höchsten Sensitivitätswert für alle möglichen Optionen zum Ausfüllen eines Antrags. In gewisser Weise berechnet diese Kennzahl, wie viele Probleme in den meisten Grenzfällen wirklich wichtig sind - in Anwendungen, deren Ergebnis am einfachsten geändert werden kann, wenn die Anwendungen selbst geringfügig geändert werden.


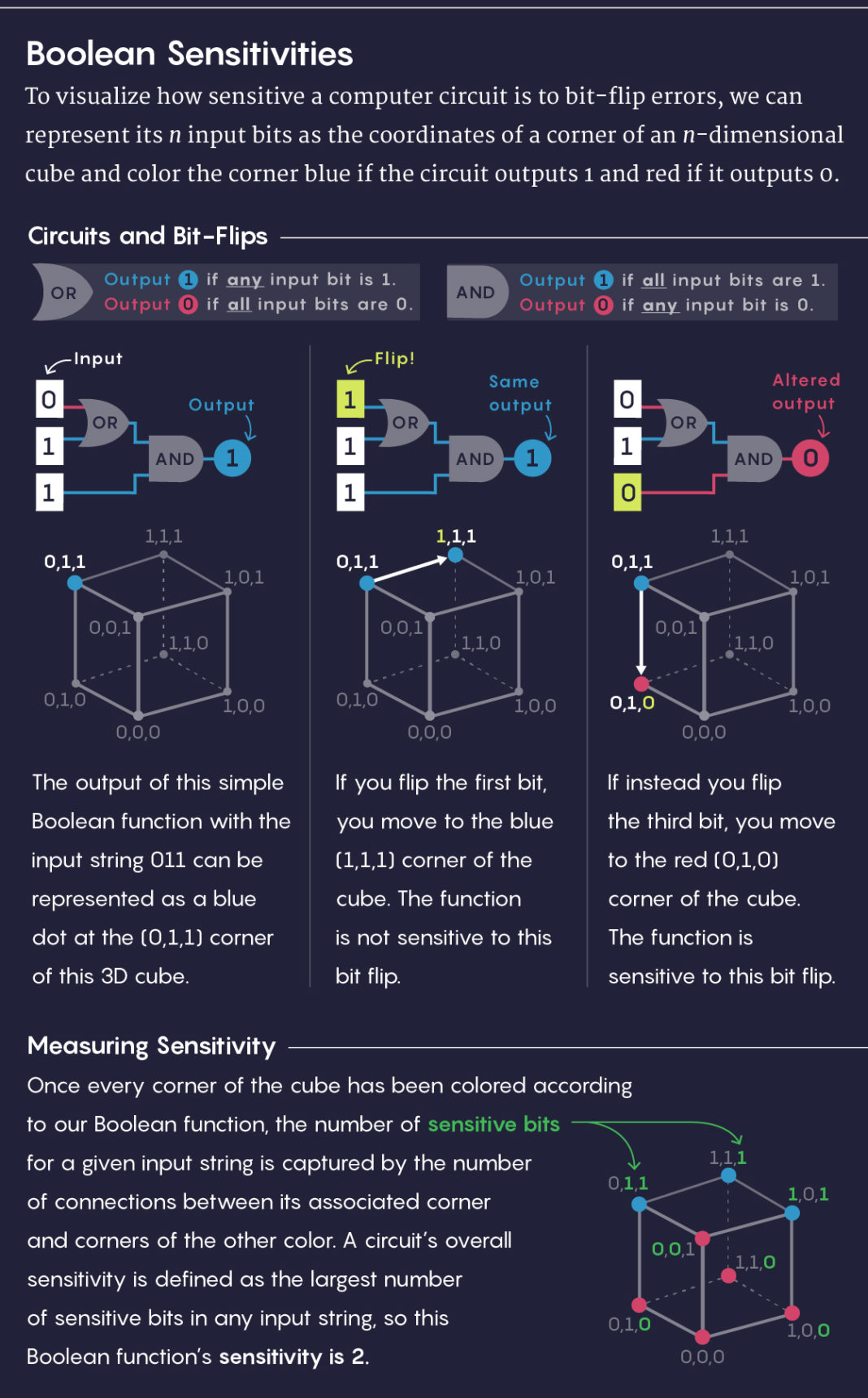Um die Empfindlichkeit der Schaltung gegenüber Fehlern bei der Umkehrung von Bits zu visualisieren, können n eingehende Bits als Koordinaten der Eckpunkte eines n-dimensionalen Würfels dargestellt werden. Wir färben den Scheitelpunkt blau, wenn der Pfad 1 ergibt, und rot, wenn 0.

In der Mitte links: Die Ausgabe einer einfachen Booleschen Funktion mit der Eingabe 011 kann durch einen blauen Punkt oben auf dem Würfel (0,1,1) dargestellt werden.
Mitte: Wenn wir das erste Bit drehen, gehen wir zur blauen Oberseite des Würfels (1,1,1). Die Funktion reagiert nicht auf die Inversion dieses Bits.
In der Mitte rechts: Wenn wir das dritte Bit drehen, gehen wir zur roten Oberseite des Würfels (0,1,0). Die Funktion reagiert empfindlich auf die Umkehrung dieses Bits.

Nachdem wir alle Scheitelpunkte des Würfels gefärbt haben, erhalten wir die Anzahl der empfindlichen Bits für eine bestimmte eingehende Linie, die der Anzahl der Verbindungen zwischen dem entsprechenden Scheitelpunkt und Scheitelpunkten einer anderen Farbe entspricht. Die Schleifenempfindlichkeit ist definiert als die größte Anzahl empfindlicher Bits in einer Eingangsleitung, daher hat diese Funktion eine Empfindlichkeit von 2.

Die Empfindlichkeit ist normalerweise eine der einfachsten Maßnahmen zur Berechnung der Komplexität, aber überhaupt keine einfache erklärende Maßnahme. Zum Beispiel könnte unser Bankier, anstatt Ihnen ein Formular zum Ausfüllen zu geben, mit einer einzelnen Frage beginnen und dann anhand Ihrer Antwort bestimmen, welche Frage als nächstes gestellt werden soll. Die größte Anzahl von Fragen, die ein Banker stellen muss, bevor er eine Entscheidung trifft, ist die Komplexität der Anforderung einer Booleschen Funktion.

Eine solche Maßnahme tritt in einer Vielzahl von Situationen auf - beispielsweise möchte ein Arzt den Patienten senden, um so wenige Tests wie möglich zu sammeln, um eine Diagnose zu stellen, oder ein Experte für maschinelles Lernen möchte möglicherweise einen Algorithmus erstellen, der so wenige Eigenschaften des Objekts wie möglich untersucht er wird es richtig klassifizieren können. "In vielen Situationen - Diagnose oder Schulung - möchten Sie, dass die Grundregel eine geringe Komplexität der Abfragen aufweist", sagte O'Donnell.

Unter anderem die Suche nach dem einfachsten Weg, eine Boolesche Funktion in Form eines mathematischen Ausdrucks zu schreiben oder zu berechnen, wie viele Antworten der Bankier dem Chef zeigen muss, um zu beweisen, dass der Antrag korrekt bearbeitet wurde. Es gibt sogar eine Variante der Komplexität der Abfrage aus der Quantenphysik, wenn der Bankier mehrere Fragen gleichzeitig „überlagert“. Um zu verstehen, wie dieses Maß mit anderen Komplexitätsmaßen zusammenhängt, verstehen die Forscher die Grenzen von Quantenalgorithmen besser.

Informatiker haben nachgewiesen, dass zwischen all diesen Maßnahmen mit Ausnahme der Empfindlichkeit ein enger Zusammenhang besteht. Insbesondere stellten sie fest, dass sie durch Polynomabhängigkeit miteinander verwandt sind - beispielsweise kann ein Maß als Quadrat oder Würfel eines anderen ausgedrückt werden. Und nur die Empfindlichkeit widerstand hartnäckig und wollte sich nicht in dieses bequeme Klassifizierungsschema integrieren. Viele Forscher vermuteten, dass es dafür geeignet sein sollte, konnten jedoch nicht beweisen, dass es keine seltsamen Booleschen Funktionen gibt, deren Empfindlichkeit mit anderen Maßen nicht durch Polynom, sondern durch exponentielle Abhängigkeit verbunden ist, was in diesem Fall bedeuten würde, dass das Sensitivitätsmaß grundsätzlich ist kleiner als der Rest.

"Diese Frage hat die Menschen 30 Jahre lang wach gehalten", sagte Aaronson.

Ecke die Lösung

Juan erfuhr von dieser Hypothese Ende 2012 bei einem Abendessen mit dem Mathematiker Michael Sachs vom Institute for Advanced Studies, wo Juan Postdoc war. Er war sofort fasziniert von der Einfachheit und Eleganz der Hypothese. "Und von diesem Moment an war ich besessen von Gedanken über sie", sagte er.

Juan fügte die Sensitivitätshypothese der „geheimen Liste“ der Probleme hinzu, an denen er interessiert war, und als er von einem neuen mathematischen Werkzeug erfuhr, fragte er sich, ob er ihm helfen könne. "Jedes Mal nach der Veröffentlichung eines anderen Werks kehrte ich zu dieser Aufgabe zurück", sagte er. "Natürlich habe ich Zeit und Energie aufgewendet, um an realistischeren Aufgaben zu arbeiten."


Hao Huang in den letzten Ferien in Lissabon

Juan wusste, wie viele in der Forschungsgemeinschaft, dass die Sensitivitätshypothese bewiesen werden kann, wenn Mathematiker eine andere Hypothese mit einer einfacheren Bedingung in Bezug auf eine Reihe von Punkten auf Würfeln unterschiedlicher Dimensionen beweisen können. Es gibt einen natürlichen Weg, von einer Folge von Nullen und Einsen zu einem Punkt auf einem n-dimensionalen Würfel zu gelangen: Verwenden Sie einfach n Bits als Koordinaten dieses Punktes.

Beispielsweise entsprechen vier Zwei-Bit-Linien - 00, 01, 10 und 11 - den vier Ecken eines Quadrats in einer zweidimensionalen Ebene: (0,0), (0,1), (1,0) und (1,1). In ähnlicher Weise entsprechen acht Drei-Bit-Zeichenfolgen acht Ecken eines dreidimensionalen Würfels usw. für höhere Dimensionen. Die Boolesche Funktion kann als Regel zum Färben dieser Würfelwinkel mit zwei verschiedenen Farben angesehen werden (z. B. Rot für 0 und Blau für 1).

Im Jahr 1992 erkannte Craig Gotsman , der jetzt am New Jersey Institute of Technology und Nati Lignal von der Hebrew University arbeitet, dass der Beweis der Sensitivitätshypothese auf die Antwort auf eine einfache Frage zu Würfeln unterschiedlicher Dimensionen reduziert werden kann: Wenn Sie einen Satz nehmen, der aus mehr als der Hälfte der Eckpunkte von Würfeln besteht und färben Sie sie rot, gibt es einen roten Punkt, der notwendigerweise mit vielen anderen roten Punkten verbunden ist (mit "verbundenen" Punkten meinen wir, dass zwei Eckpunkte durch eine gemeinsame Kante verbunden sind und nicht lokalisiert sind diagonal).

Wenn unsere Teilmenge genau die Hälfte der Eckpunkte des Würfels enthält, sind sie möglicherweise nicht miteinander verbunden. Unter den acht Ecken eines dreidimensionalen Würfels befinden sich beispielsweise vier Punkte:
(0,0,0), (1,1,0), (1,0,1) und (0,1,1) liegen diagonal voneinander. Sobald jedoch mehr als die Hälfte der Eckpunkte eines Würfels einer beliebigen Dimension rot wird, müssen rote Punkte untereinander verbunden werden. Die Frage ist, wie diese Verbindungen verteilt sind. Wird es mindestens einen dieser Peaks mit mehr Verbindungen geben?

Im Jahr 2013 begann Juan zu glauben, dass der beste Weg, um dieses Problem zu verstehen, wahrscheinlich darin besteht, die Standardmethode zur Darstellung des Netzwerks mithilfe einer Matrix zu verwenden, die verfolgt, welche Punkte verbunden sind, und dann viele Zahlen untersucht, die als Eigenwerte der Matrix bezeichnet werden. Fünf Jahre lang kehrte er regelmäßig zu dieser Idee zurück, aber ohne Erfolg. "Zumindest aufgrund dessen, was ich vor dem Schlafengehen über sie dachte, war es für mich einfacher, viele Nächte zu schlafen", kommentierte er Aaronsons Blogbeitrag.

Dann, im Jahr 2018, dachte Juan darüber nach, den Cauchy-Wechselsatz zu verwenden, eine mathematische Aussage von vor 200 Jahren, die die Eigenwerte einer Matrix mit einer Submatrix verbindet, was sie möglicherweise zu einem idealen Werkzeug für die Untersuchung der Beziehung zwischen einem Würfel und einer Teilmenge seiner Eckpunkte macht. Juan beschloss, ein Stipendium der State Science Foundation zu beantragen, um diese Idee weiter zu untersuchen.

Als er letzten Monat in einem Hotel in Madrid saß und einen Zuschussantrag ausfüllte, wurde ihm plötzlich klar, dass er diesen Ansatz bis zum Ende ausweiten konnte, indem er einfach die Vorzeichen einiger Zahlen aus der Matrix änderte. Auf diese Weise konnte er beweisen, dass in jeder Menge von mehr als der Hälfte der Eckpunkte eines n-dimensionalen Würfels ein Punkt existiert, der mindestens √n anderen Punkten zugeordnet ist - und die Sensitivitätshypothese folgt unmittelbar aus diesem Ergebnis.

Als Matthew Juans Arbeit per Post erhielt, war ihre erste Reaktion "Ups", sagte sie. „Wenn eine Aufgabe seit 30 Jahren besteht und jeder davon weiß, muss ihr Beweis entweder sehr lang und komplex oder sehr tief sein.“ Sie öffnete die Akte mit der Arbeit und erwartete, dass sie nichts verstehen würde.

Der Beweis war jedoch so einfach, dass Matthew und andere Forscher ihn in einer Sitzung verdauen konnten. "Ich denke, dass die Studenten ihn diesen Herbst als Teil einer Vorlesung in jedem Masterstudiengang in Kombinatorik erzählen werden", schrieb sie über Skype.

Das Ergebnis von Juan erwies sich als noch stärker als nötig, um diese Hypothese zu beweisen, und diese Kraft sollte uns neue Ideen über Komplexitätsmaße geben. "Es wurde unserem Toolkit hinzugefügt und kann bei der Beantwortung anderer Fragen zu Booleschen Funktionen hilfreich sein", sagte Cenedio.

Vor allem aber erlaubt uns das Ergebnis von Juan, alle Sorgen darüber zu beenden, ob Sensibilität in der Welt der Komplexitätsmaße ein seltsamer Außerirdischer ist, sagte Cenedio. "Ich denke, dass am Abend, als sie von diesen Ergebnissen erfuhren, sehr viele in der Lage waren, friedlich zu schlafen."