Mit komplexen Zahlen spielen

Hallo!

Ein weiterer Aufsatz. Dieses Mal spielen wir mit komplexen Zahlen, mit Formeln und deren Visualisierung.

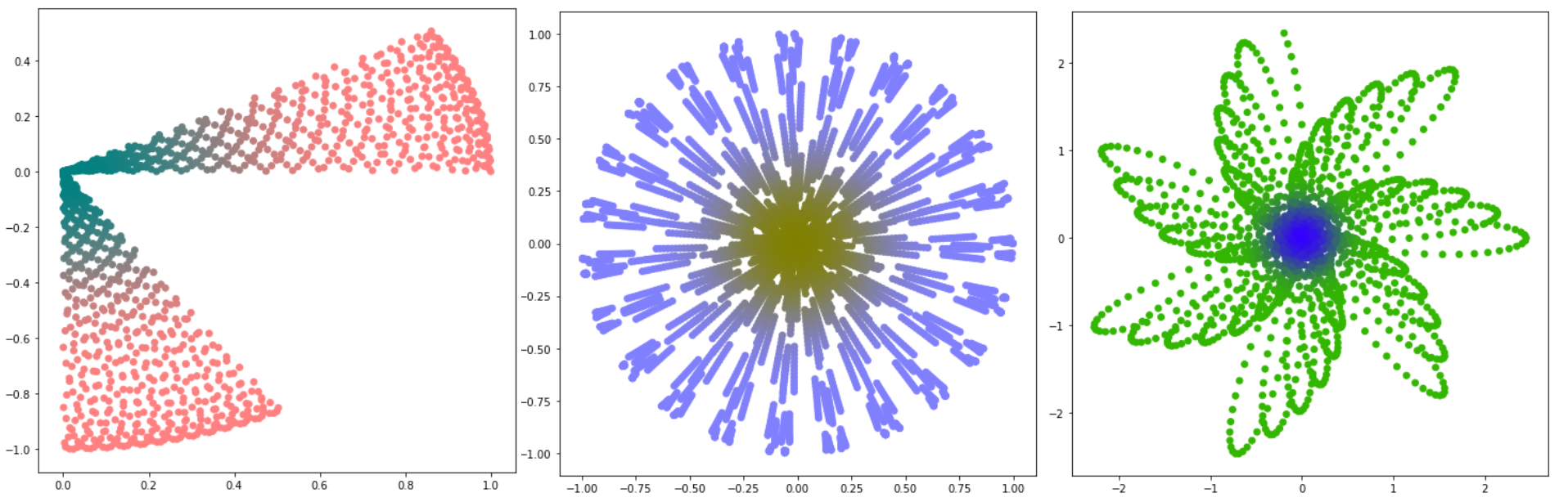
Idee

Eine komplexe Zahl ist eine bestimmte Erweiterung einer reellen Zahl, in der Tat ein Vektor, für den eine ganze Reihe von Axiomen definiert ist. Jede komplexe (und damit reelle) Zahl kann als geschrieben werden $$$z = a + bi$ wobei a der Realteil ist, b der Imaginärteil ist, i die Wurzel der Gleichung ist $$$x ^ {2} = - 1$ . Dafür sind viele Operationen definiert, die beispielsweise für eine reelle Zahl definiert sind $$$z_1 + z_2 = a_1 + a_2 + (b_1 + b_2) i$ . Interessanterweise, wenn Sie verschiedene Operationen mit ihnen ausführen, erhöhen Sie auf eine Potenz, multiplizieren Sie usw. und nehmen Sie dann $$$Re (z)$ (Realteil) für die Achse Ox und $$$Im (z)$ (Imaginärteil) Für die Oy-Achse können Sie lustige Bilder erhalten.

Übrigens habe ich mir alle folgenden Formeln ausgedacht.

Visualisierungsfunktion

Routine. Die Funktion, die nach dieser iterativen Funktion alles auf das Feld zeichnet:

import random import numpy as np def vis(A, f, step=1.0, c=None): x = [] y = [] for B in np.arange(0, A, step): v = f(A, B) x.append(v.real) y.append(v.imag) plt.figure(figsize=[8, 8]) mxabs = max([i[0] ** 2 + i[1] ** 2 for i in zip(x, y)]) ** 0.5 x = np.array(x) / mxabs y = np.array(y) / mxabs if c is None: plt.scatter(x, y) else: plt.scatter(x, y, color=[c(x[i], y[i]) for i in range(len(x))]) plt.show() 

Alle unsere Funktionen hängen von zwei Parametern A und B ab. Außerdem iterieren wir innerhalb von vis () über B, und A ist der globale Parameter der Funktion.

Die Curl-Funktion

$$

$$f (A, B) = Bsin (B) * e ^ {iBcos (A)}$$

Ihre Erklärung in Python:

 def func_1(A, B): return math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) 

Und renn

 A = 121.5 vis(A, func_1, step=0.1) 

Und das Ergebnis für A = 121,5:



Und für A = 221,5:



Beachten Sie, dass diese Zahlen nicht aus der Berechnung eines bestimmten Integrals auf einer glatten Mannigfaltigkeit und anderen in diesem Zusammenhang bedeutungslosen intelligenten Wörtern folgen. Dies sind wirklich Zufallszahlen, und es gibt immer noch genau unendlich viele verschiedene A, was zu Schönheit führt.

Müssen malen

Wir deklarieren eine Farbfunktion (eine solche Funktion, die ein Tupel von drei Zahlen in Koordinaten zurückgibt):

 def sigm(x): #         0  1 return (1 / (1 + 1.2 ** (-x*50)) - 0.5) * 2 color_1 = lambda x, y: (0.2, sigm(x ** 2 + y ** 2) / 1.4, 1 - sigm(x ** 2 + y ** 2)) color_2 = lambda x, y: (sigm(x ** 2 + y ** 2), 0.5, 0.5) 

Wählen Sie den Zufallsparameter A und lassen Sie ihn 149 sein:

 vis(149, func_1, step=0.1, c=color_1) 

Gänsefunktion

Gänse werden wie folgt beschrieben:

$$

$$f (A, B) = cos (B) sin (B) * B * e ^ {iBcos (A)}$$

Python-Deklaration:

 def func_2(A, B): return math.cos(B) * math.sin(B) * B * math.e ** (1j * (B * math.cos(A))) 

Sein Ergebnis für A = 106:

Focaccia-Funktion

$$

$$f (A, B) = cos (B (A + 1)) * e ^ {iBcos (A)}$$

 def func_3(A, B): return math.cos((A + 1) * B) * math.e ** (1j * (B * math.cos(A))) 

 vis(246, func_3, step=0.1, c=color_2) 

 vis(246, func_3, step=0.1, c=color_2) 

Funktion ohne Titel

$$

$$f (A, B) = Bsin (A + B) * e ^ {iBsin (A)}$$

 color_3 = lambda x, y: (0.5, 0.5, sigm(x ** 2 + y ** 2)) vis(162, func_4, step=0.1, c=color_3) 

 vis(179, func_4, step=0.1, c=color_3) 

Schönheitsformel

$$

$$f (A, B) = cos (B (A + 1)) ^ {\ frac {3} {2}} * e ^ {iBcos (A)}$$

 def func_5(A, B): return math.cos((A + 1) * B) ** 1.5 * math.e ** (1j * (B * math.cos(A))) 

 color_4 = lambda x, y: (sigm(x ** 2 + y ** 2) / 2, 0.5, 1 - sigm(x ** 2 + y ** 2)) vis(345, func_5, step=0.1, c=color_4) 

 vis(350, func_5, step=0.1, c=color_4) 

Das ist alles für jetzt.