"Technologie" zum Erhalten von Gleichungen der Dynamik von TAU. Und warum ist Systemidentifikation scheiße und "ehrliche Physik" Regeln

Bei der Erörterung des vorherigen Artikels über modellorientiertes Design stellte sich eine vernünftige Frage: Wenn wir die Daten des Experiments verwenden, aber es noch einfacher ist, die Daten in die Systemidentifikation aufzunehmen und das Modell des Objekts zu erhalten, ohne sich um die Physik zu kümmern? Ohne mit Rabinovichi alle möglichen mehrstöckigen Formeln von Navier-Stokes, Bernoulli und anderen Bremssattelkompassen zu studieren? Wir haben das Objekt getestet - haben das Ergebnis erhalten.



Wir haben das FAU2-Raketenmodell als einzelne Übertragungsfunktion vorgestellt, Sie können es hier sehen ... Und anscheinend hat alles funktioniert. Warum müssen wir zuerst die mathematische Analyse und die Differentialrechnung studieren, wenn es einen magischen Knopf gibt, der das Modell aus den Tests erhält?

Dieser Ansatz kann zwar angewendet werden, erfordert jedoch zwei Bedingungen:

• Das Objekt sollte bereits sein (nicht für entworfene Objekte geeignet).
• Messdaten müssen vollständig und zuverlässig sein.

In allen anderen Fällen - „sie wollten das Beste, es stellte sich wie immer heraus“ (c).
In diesem Artikel über die Simulation eines elektrischen Antriebs wird beispielsweise gezeigt, dass „für einen bestimmten Schwellenwert der Genauigkeit von Messgeräten das Antriebsmodell nicht mehr identifizierbar ist, was zu einem Verlust der Steuerbarkeit und der Unfähigkeit zur Diagnose führt“.
Im selben Artikel werden wir die Magie und Magie der Erstellung von Modellen in Form von Übertragungsfunktionen von TAU analysieren und anschließend eine Sitzung zur Aufdeckung dieser Magie durchführen.

Also zuerst die Magie

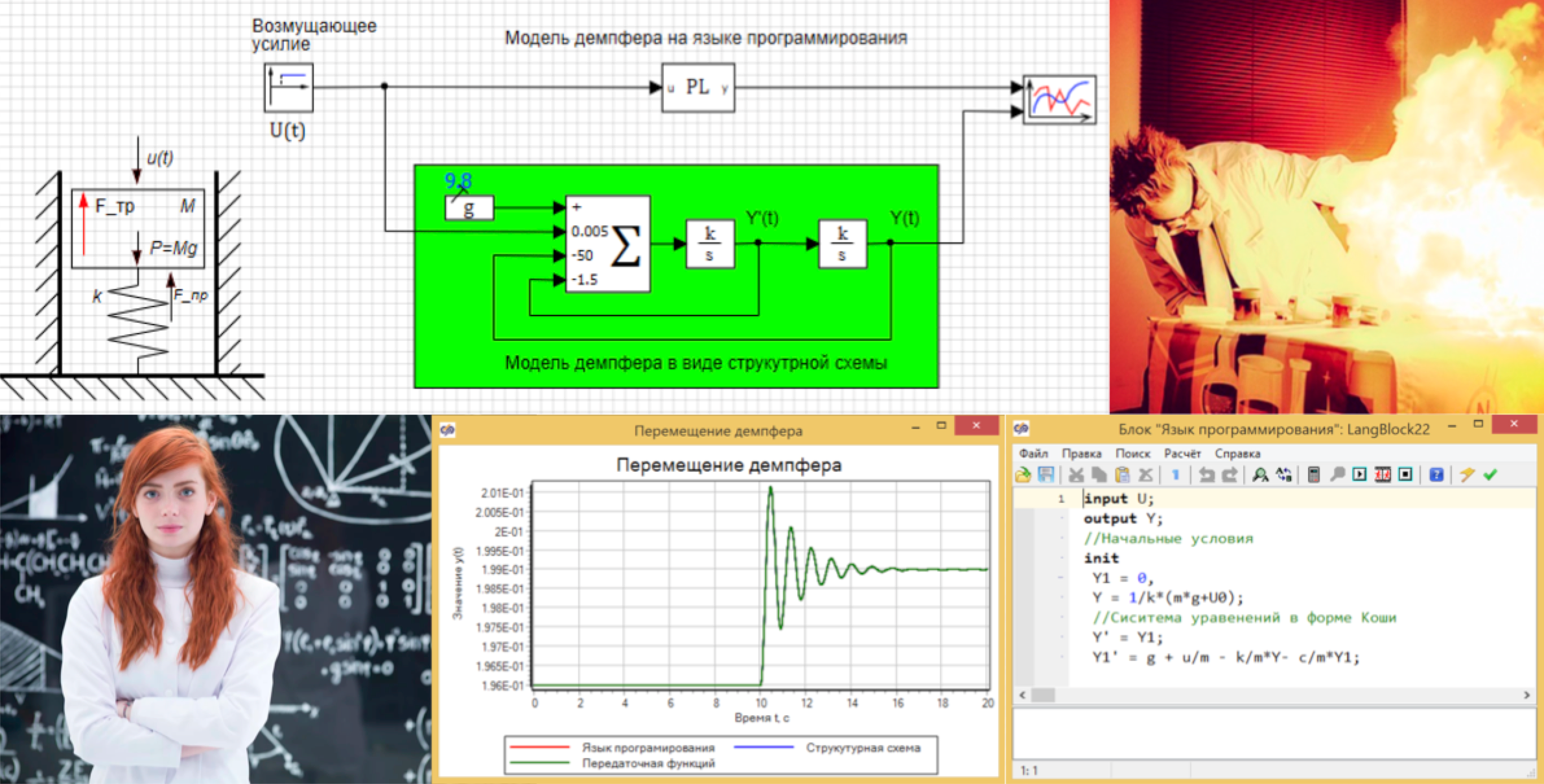
Schauen wir uns ein einfaches Beispiel an. Wir haben ein Modell eines mechanischen Dämpfers. Dies ist ein Kolben an einer Feder, er bewegt sich im Zylinder, er kann sich auf und ab bewegen. Seine Position ist die Funktion Y (t), die uns interessiert, die Störkraft (U (t)) wirkt von oben auf sie und die Kraft der viskosen Reibung wirkt auf die Kolbenwände. (Siehe Abb. 1)


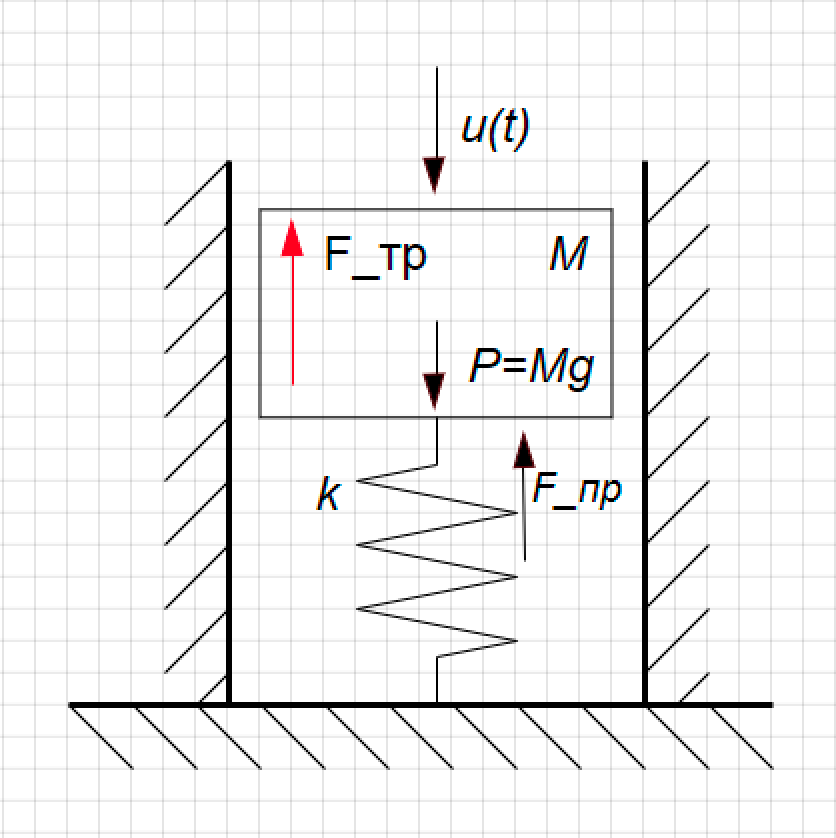Abbildung 1. Aufbau des Stoßdämpfers.

Wir leiten die Übertragungsfunktion für diesen Link ab.

Diejenigen Jedi, die bereits mit der Magie der Übertragungsfunktionen vertraut sind, können diesen Teil überspringen und direkt die Magie aufdecken. Für die jungen Padawaner werden wir die gesamte Technologie zum Erhalten dynamischer Gleichungen enthüllen.

Nach dem 2. Newtonschen Gesetz ist die Beschleunigung des Körpers proportional zur Summe der auf den Körper einwirkenden Kräfte:

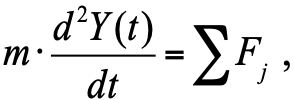
, (1)
wobei m das Körpergewicht ist; F _j - auf den Körper wirkende Kräfte (Dämpferkolben).
Einsetzen aller Kräfte gemäß Fig. (1) gemäß Fig. 1 haben wir:

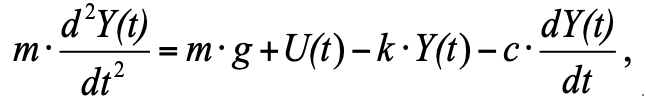
(2)
wo:
Y (t) ist die Position des Kolbens;
P = m ≤ g - Schwerkraft;
F_pr = k ∙ Y (t) - Federwiderstandskraft ;
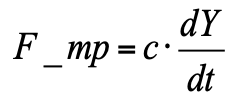
- viskose Reibungskraft (proportional zur Kolbengeschwindigkeit).
Abmessungen der in Gleichung (2) enthaltenen Kräfte und Koeffizienten:


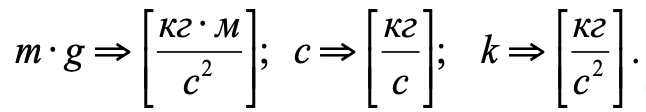
Wir glauben, dass sich der Kolben zum Zeitpunkt Null im Gleichgewicht befindet. Dann ist die Anfangsposition des Kolbens y ₀ im Gleichgewicht, wobei die Geschwindigkeit und Beschleunigung 0 sind, kann aus Gleichung 2 berechnet werden.



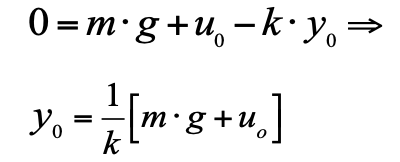
Mit dieser Gleichung können Sie berechnen, in welcher Position sich der Kolben bei unterschiedlichen Belastungen befindet. Diese statische Eigenschaft: aufgebrachte Kraft - empfangene Verschiebung. Das Erscheinungsbild unseres Systems ist äußerst einfach (siehe Abb. 2):


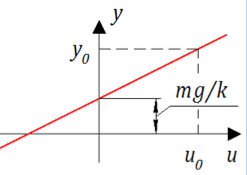Abbildung 2. Statische Charakteristik des Dämpfers.

Es scheint, dass es hier Glück ist - eine einfache Linie, wenn es Kraft anwendet, erhält es Verschiebung. Aber da war es! Wir interessieren uns nicht für die endgültige Position des Kolbens, sondern für den Übergang von einem Zustand in einen anderen.

Um den transienten Prozess zu analysieren, wurde die Theorie der automatischen Steuerung der TAU erstellt. Gemäß einer typischen "Technologie zur Erstellung von Modellen" gemäß dieser Theorie wird vorgeschlagen, das System nicht in absoluten Werten, sondern in Abweichungen vom Gleichgewichtszustand zu betrachten. Eine solche Aussage vereinfacht die Lösung und den Aufbau. Und tatsächlich erhalten wir, wenn wir die absoluten Werte durch Abweichungen ersetzen:


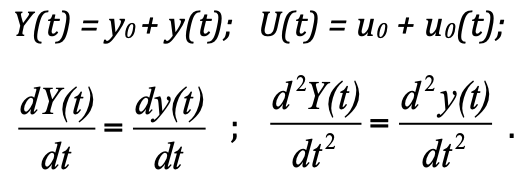F_pr = k ≤ (y ₀ + y (t)) = k ≤ y ₀ + k ≤ y (t) ist die Widerstandskraft der Feder;
- Reibungskraft.
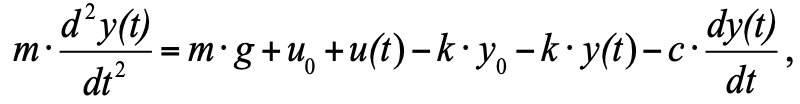
aber da wir akzeptiert haben, dass wir im Anfangsmoment einen Gleichgewichtszustand haben und die Summe der drei Kräfte im Gleichgewichtszustand Null ist, können wir sie aus der Gleichung entfernen, und als Ergebnis erhalten wir:

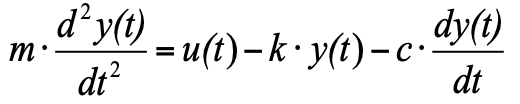
(4)
Um die Gleichung in die Form gemäß dem Kanon von TAU zu übersetzen, müssen Sie die gesamte Gleichung durch k teilen, so dass der Koeffizient y, der Wert der Ausgangsvariablen gleich 1 ist, und die Faktoren mit den Ausgangswerten von y (t) auf die rechte Seite und die Eingabewerte auf die linke Seite übertragen beeinflusst u (t) :

(5)
Diese Gleichung kann bereits in Operatorform geschrieben werden:

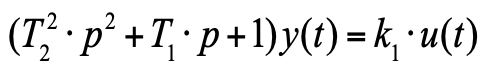
(6)
wo:


p = d / dt ist der Differenzierungsoperator. Beachten Sie, dass die Dimensionen der Koeffizienten die Dimension und Bedeutung von Zeitkonstanten haben:



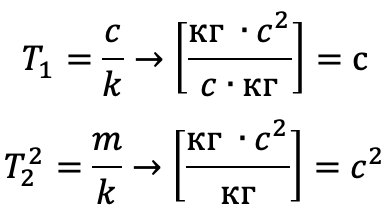
Eine Übertragungsfunktion für eine solche Gleichung [6] hat die Form:


Vor Ihren Augen haben wir die Übertragungsfunktion in Form eines Blocks aus den Gleichungen der Physik erhalten, und außerdem ist der resultierende Block eine Standard-Oszillationsverbindung von TAU.

Für mich persönlich ist die Magie hier das magische Erscheinungsbild statischer Eigenschaften, Teile des Systems, Masse des Kolbens, Federelastizität, Reibung an den Wänden) des Objekts, das auf magische Weise als vorübergehende Eigenschaft von Transienten im System erschien

Überprüfen Sie die Formeln mit dem Modell

Wie Maxim Andreev mir bei der Erstellung dynamischer Modelle beigebracht hat: „Das Ende ist der Kopf von allem!“ ( siehe hier das zweite Prinzip der Modellierung - „vom Ende beginnen“ ):

Und am Ende der Funktion haben wir Bewegung.

Stellen Sie sich daher Gleichung 2 in Form von Cauchy vor, um sich zu bewegen.

Die Cauchy-Form ist, wenn links Ableitungen der für uns interessanten Funktionen sind, rechts Ausdrücke für ihre Berechnung. Da die Ableitung in der Gleichung zweiten Grades ist und eine neue Variable Y1 einführt - die Änderungsrate der Position (Verschiebungsgeschwindigkeit), erhalten wir ein System aus zwei Gleichungen in Form von Cauchy:



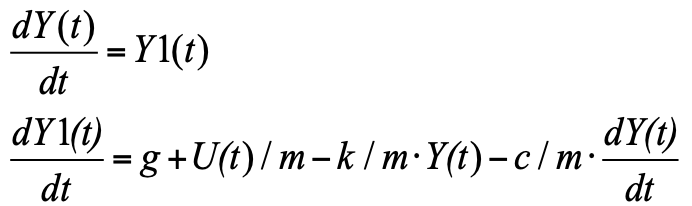
Diese Gleichung kann einfach in den Block "Programmiersprache" geschrieben werden und das Modell erhalten (siehe Abb. 3):


Abbildung 3. Ein Dämpfungsmodell in einer Programmiersprache.

Als Eingabe verwenden wir den Wert der Kraft U, die Ausgabe des Blocks ist die Verschiebung Y, die Anfangsposition wird durch die Formel 3 angegeben. Alle Variablen werden als globale Signale für das Projekt festgelegt:


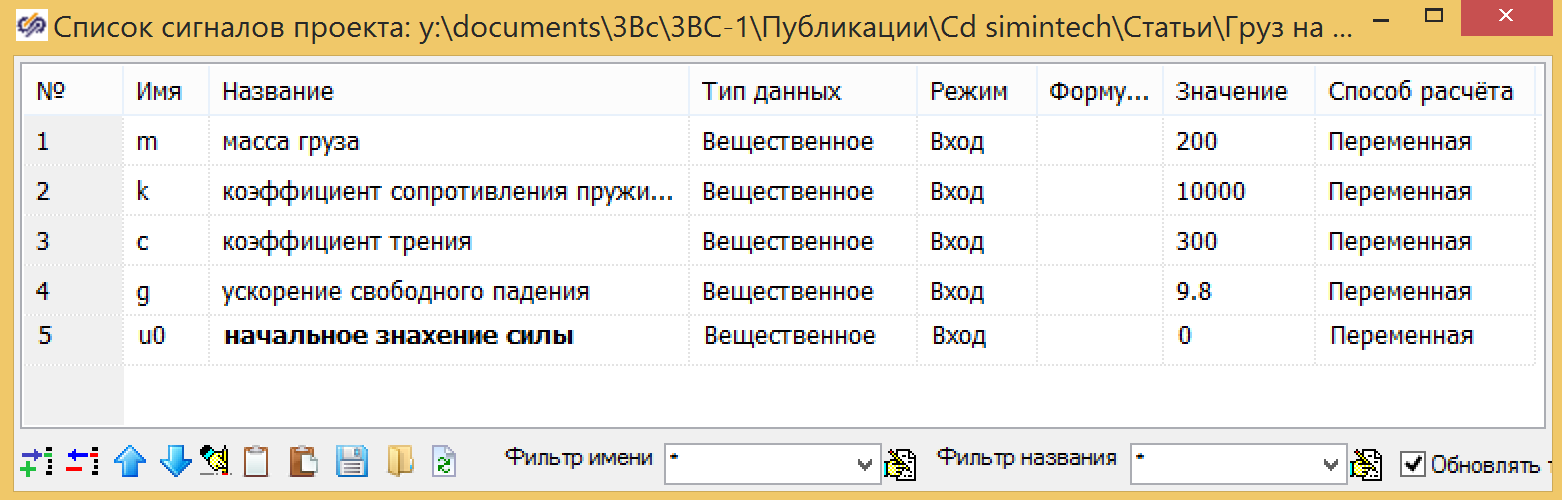Abbildung 4. Globale Projektvariablen.

Das Dämpfungsmodell kann auch in Form einer Struktur in 5 erstellt werden, die ein paralleles Dämpfungsmodell zeigt, das aus Standardblöcken erstellt wurde, in denen sich die Anfangsbedingung im Integrator am Ausgang befindet (siehe 6) und die Koeffizienten in den Addierer eingegeben werden (siehe 6). 7)


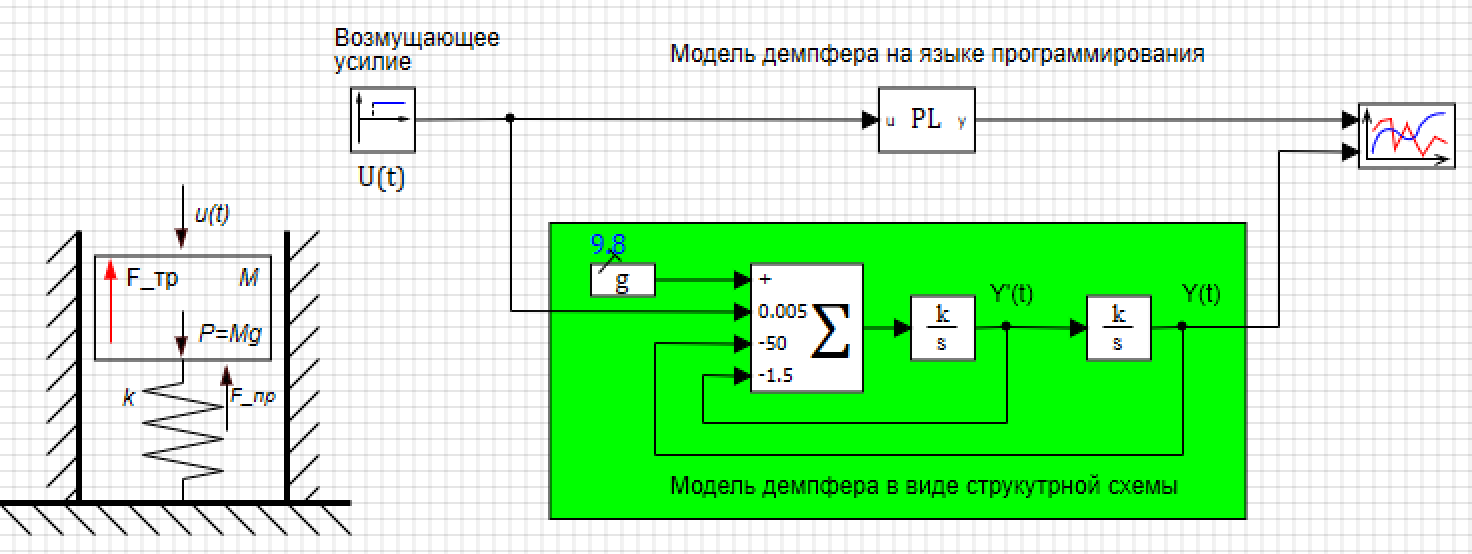Abbildung 5. Dämpfer in einer Programmiersprache und in Form eines Strukturdiagramms.


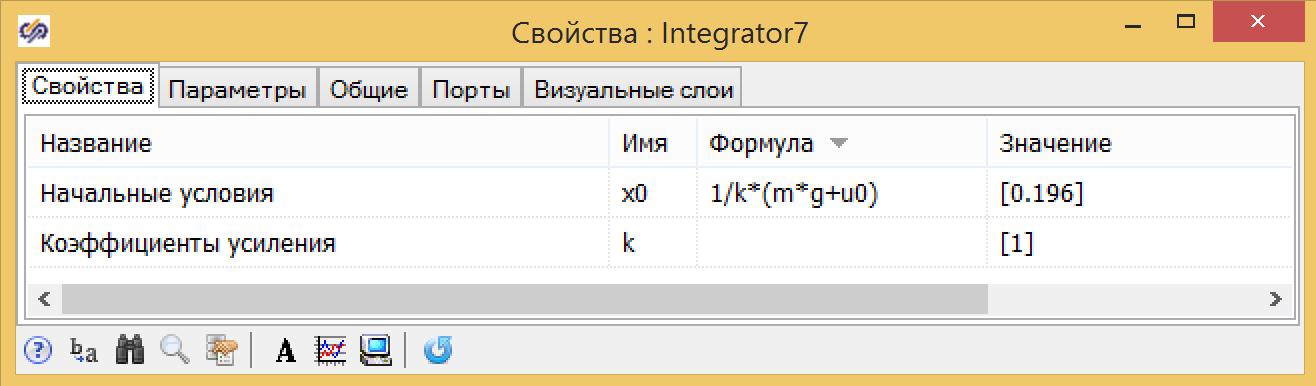Abbildung 6. Integrator-Eigenschaft mit Anfangsbedingungen.


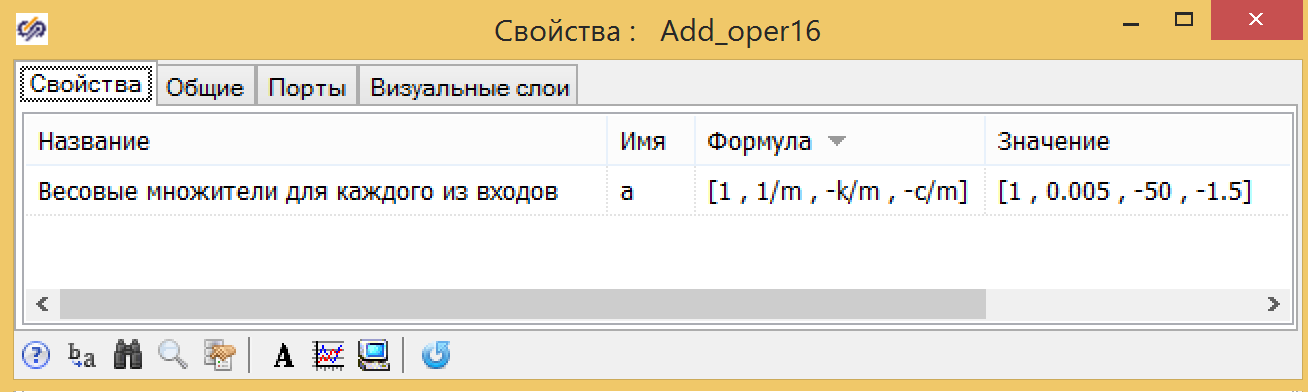Abbildung 7. Eigenschaften des Addierers mit Koeffizienten.

Wir stellen den Störungseffekt für 10 Sekunden ein, indem wir die wirkende Kraft in einem Sprung von 0 auf 30 ändern und sicherstellen, dass die beiden Modelle das gleiche Ergebnis zeigen (siehe Abb. 8).


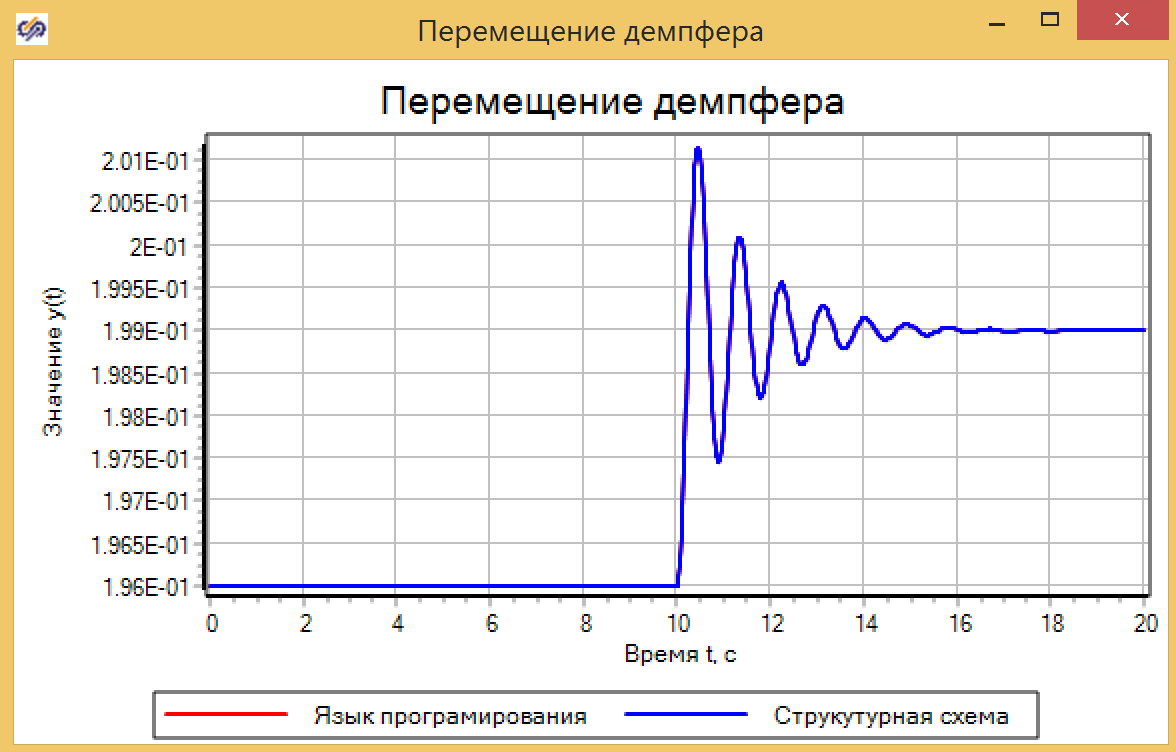Abbildung 8. Bewegen des Dämpfers.

Lassen Sie uns das Modell in Form einer Übertragungsfunktion in allgemeiner Form und in Form einer oszillierenden Verbindung überprüfen, die dieses System ist. Dazu bauen wir die Schaltung zusammen, wie in Abbildung 9 dargestellt.


Abbildung 9. Zwei Dämpfermodelle in Form von Übertragungsfunktionen.

Es muss berücksichtigt werden, dass wir das Diagramm in Abweichungen zusammengestellt haben. Um den absoluten Wert zu erhalten, muss daher eine Konstante hinzugefügt werden - die Anfangsposition des Kolbens.

Für die Übertragungsfunktion (Formel 7) verwenden wir dieselben globalen Konstanten und Ausdrücke, die zuvor für k ₁ , T ₁ , T _{2 erhalten wurden} (siehe 10).


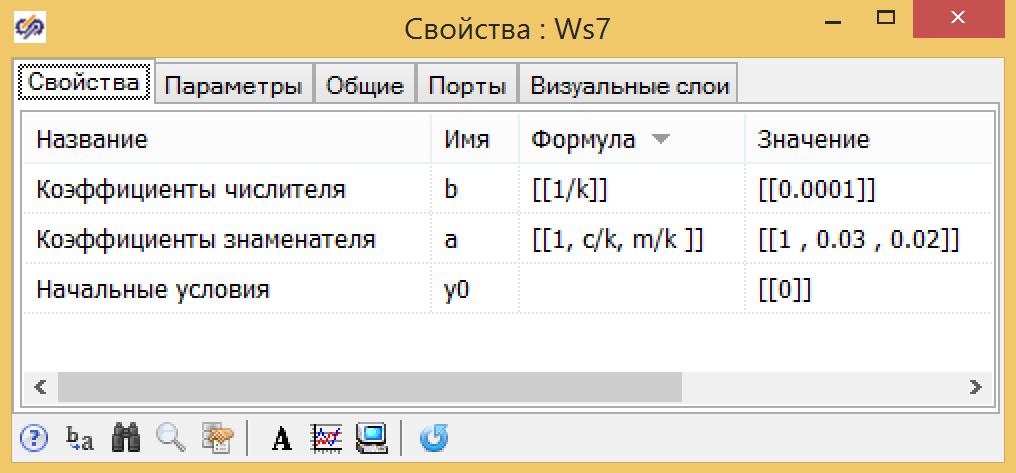Abbildung 10. Parameter der Übertragungsfunktion des allgemeinen Formulars.

Für die Parameter der Schwingungsverbindung sind die Formeln etwas komplizierter, sie können jedoch auch als globale Parameter ausgedrückt werden: Kolbenmasse m, Federwiderstandsbeiwert k, Reibungskoeffizient s (siehe Abb. 11).


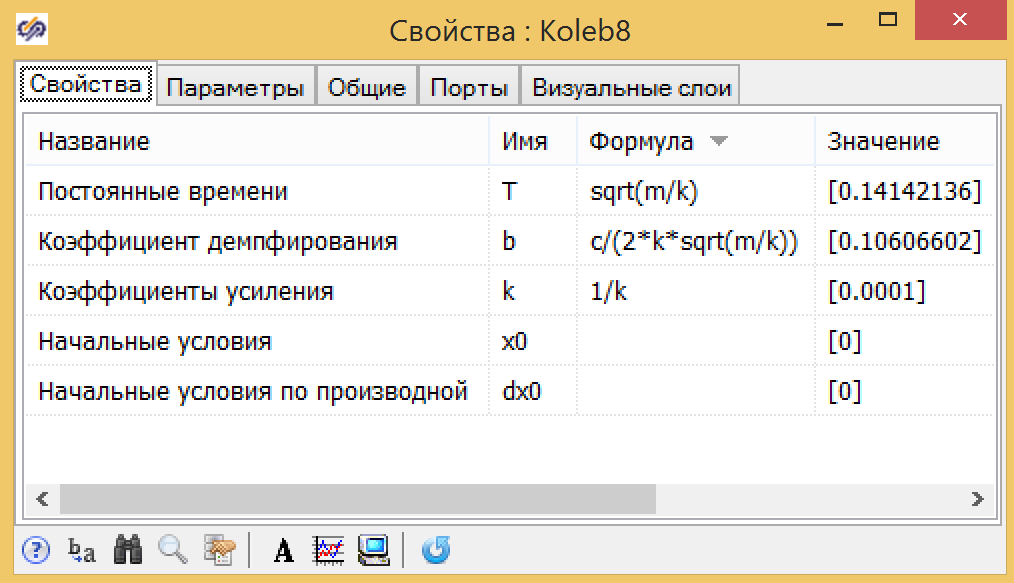Abbildung 11. Parameter der Schwingungsverbindung.

Übergangsgraphen zeigen (siehe Abbildung 12), dass TAU-Magie wirklich funktioniert. Die Übertragungsfunktion liefert genau die gleichen Ergebnisse wie ein Modell, das auf physikalischen Gleichungen basiert.


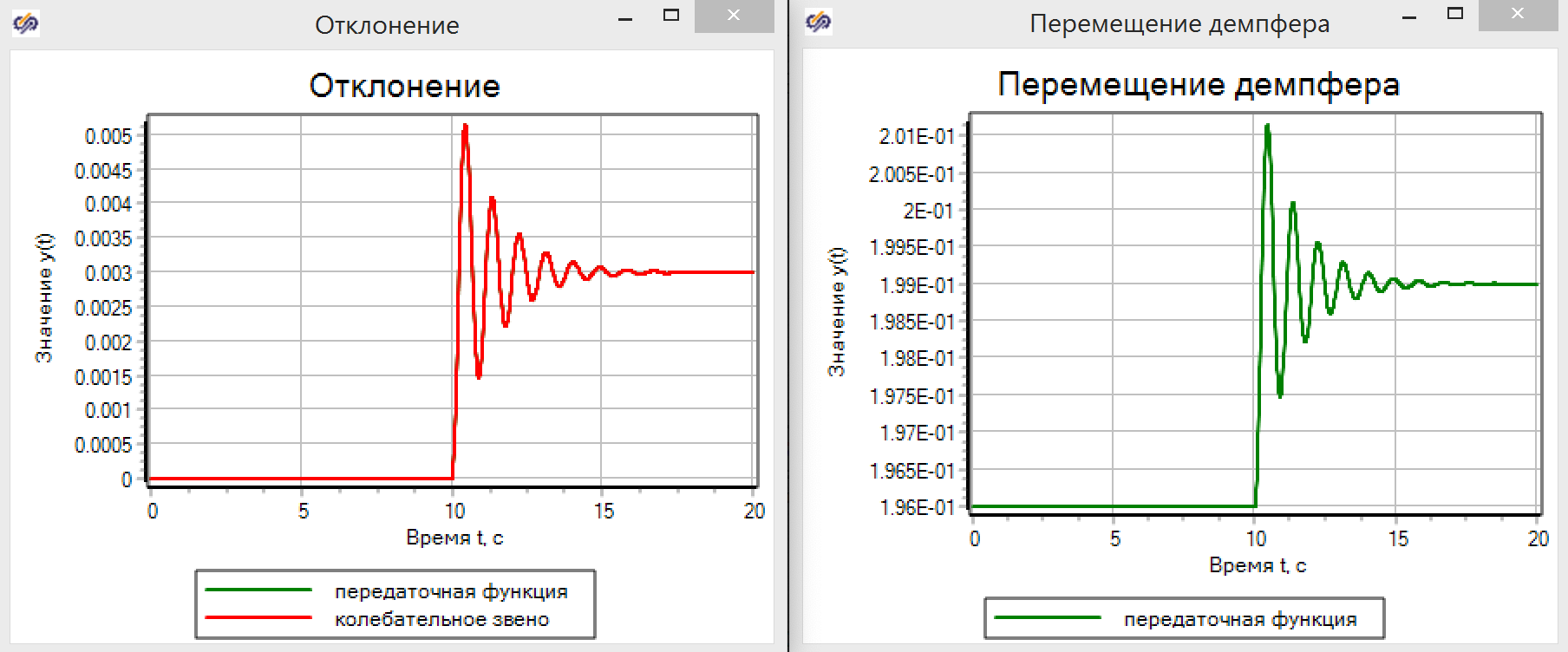Abbildung 12. Bewegen des Dämpfers in TAU-Modellen.

Stellen Sie sich vor, wir haben kein Modell und verwenden eine Identifikationseinheit gemäß den aus dem Experiment erhaltenen Daten. Es gibt eine ganze Technologie von Datenanalyse- und Übertragungsfunktionen, aber als Teil des Artikels und als Beispiel werden wir den Baustein der Übertragungsfunktion in Form einer Programmiersprache mit dem Modell verbinden, wie in Abbildung 13 gezeigt. Wir glauben, dass wir ein „Black-Box“ -Modell haben, und Wir wissen nicht, was drin ist.


Abbildung 13. Das Verbindungsschema der Pseudokennung.

Als Ergebnis der Analyse unseres Blocks in einer Programmiersprache haben wir eine Übertragungsfunktion erhalten, die sich praktisch nicht von der ursprünglichen unterscheidet und aus den Gleichungen abgeleitet wurde (siehe Abb. 14). Vergleiche mit Abbildung 10. Hier ist es ein magischer Knopf!


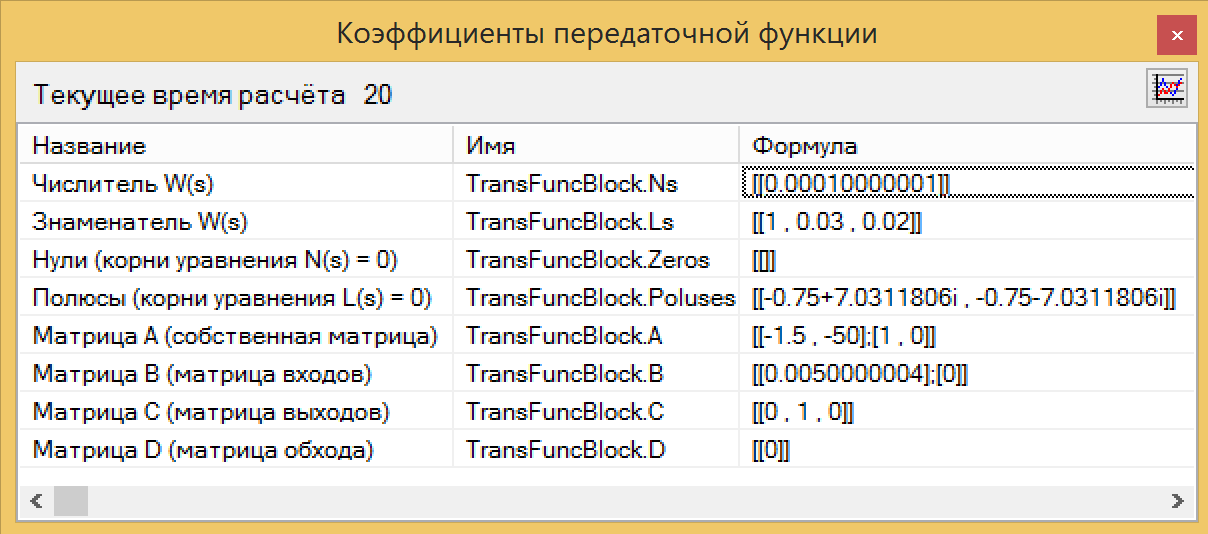Abbildung 14. Identifizierung der Übertragungsfunktion.

Die Zähler- und Nennerwerte können direkt aus dem Identifikationsblock kopiert, in den Übertragungsfunktionsblock eingefügt und sichergestellt werden, dass die Diagramme übereinstimmen. TAU Magie funktioniert.

Sitzung der Enthüllung von Magie

Warum können Sie die Systemidentifikation nicht immer für einen modellorientierten Entwurfsprozess verwenden, wenn alles so magisch ist?

Um den Nachteil der Modelle zu verstehen, die durch Identifizieren der Blackbox Systemidentifikation erhalten wurden, versuchen Sie, eine einfache Frage zu beantworten: Wie groß ist die Abweichung des Dämpfers, wenn die Kolbenmasse um 30% erhöht wird?

Und dann stellt sich heraus, dass nicht alle Joghurts gleich nützlich sind.

Wenn Sie ehrliche Gleichungen haben, ändern Sie einfach die Masse der Last in den globalen Variablen des Projekts und erhalten einen neuen Übergangsprozess und eine neue Übertragungsfunktion.



Wenn Sie anstelle von ehrlichen Gleichungen der Physik eine vorgefertigte Übertragungsfunktion haben, die aus den Ergebnissen des Experiments erstellt wurde, müssen Sie erneut ausführen und das Experiment durchführen, um zu verstehen, wie sich die Änderung der Masse auf das Verhalten des Modells auswirkt. Wie sie sagen, gibt ein schlechter Kopf den Beinen keine Ruhe.

Schlussfolgerungen:

1. Sich hinzusetzen und über die Gleichungen der Physik nachzudenken, ist immer vorteilhafter und billiger als das Experimentieren.
2. Ein aus den physikalischen Gleichungen von Prozessen abgeleitetes Modell ist viel schmackhafter und nützlicher als Übertragungsfunktionen.
3. Das Experiment sollte unbekannte Koeffizienten oder schwer zu messende Parameter klären.
4. Lerne Physik und du wirst glücklich sein!

Die Datei mit dem Dämpfermodell für Experimente kann hier entnommen werden ...