Dies ist eine schrittweise Anleitung zur Klassifizierung multispektraler Bilder vom Landsat 5-Satelliten. In einer Reihe von Bereichen dominiert heute das tiefe Lernen als Werkzeug zur Lösung komplexer Probleme, einschließlich geografischer Probleme. Ich hoffe, Sie sind mit Satellitendatensätzen vertraut, insbesondere mit Landsat 5 TM. Wenn Sie mit Algorithmen für maschinelles Lernen ein wenig vertraut sind, können Sie dieses Handbuch schnell erlernen. Und für diejenigen, die nicht verstehen, ist es ausreichend zu wissen, dass maschinelles Lernen tatsächlich darin besteht, Beziehungen zwischen mehreren Merkmalen (einer Menge von Attributen X) eines Objekts mit seiner anderen Eigenschaft (Wert oder Bezeichnung, die Zielvariable Y) herzustellen. Wir füttern das Modell mit vielen Objekten, für die die Eigenschaften und der Wert des Zielindikators / der Zielklasse des Objekts bekannt sind (beschriftete Daten), und trainieren es so, dass es den Wert der Zielvariablen Y für neue Daten vorhersagen kann (nicht markiert).
Was ist das Hauptproblem bei Satellitenbildern?
Zwei oder mehr Klassen von Objekten (z. B. Gebäude, Baulücken und Fundamentgruben) in Satellitenbildern können die gleichen spektralen Eigenschaften des Werts aufweisen. Daher war ihre Klassifizierung in den letzten zwanzig Jahren eine schwierige Aufgabe.
Aus diesem Grund ist es möglich, klassische Modelle des maschinellen Lernens mit und ohne Lehrer zu verwenden, aber ihre Qualität ist alles andere als ideal. Sie haben immer die gleichen Nachteile. Betrachten Sie ein Beispiel:
Wenn Sie eine vertikale Linie als Klassifikator verwenden und entlang der X-Achse verschieben, ist das Klassifizieren von Bildern von Häusern nicht einfach. Die Daten werden so verteilt, dass es unmöglich ist, sie mit einer vertikalen Linie in Klassen zu unterteilen (in solchen Fällen heißt es, dass "Objekte verschiedener Klassen nicht linear trennbar sind"). Dies bedeutet jedoch nicht, dass Häuser überhaupt nicht klassifiziert werden können!
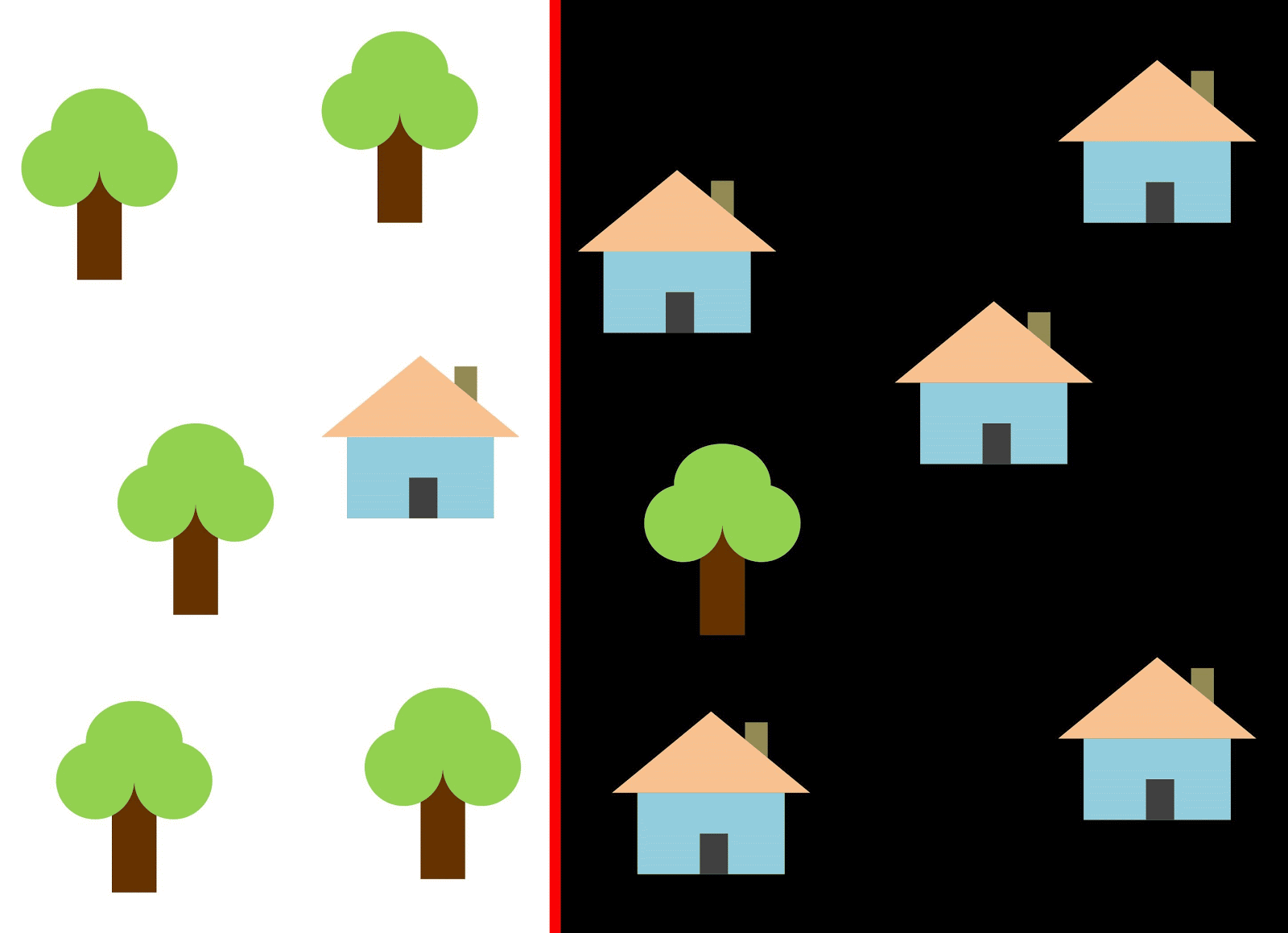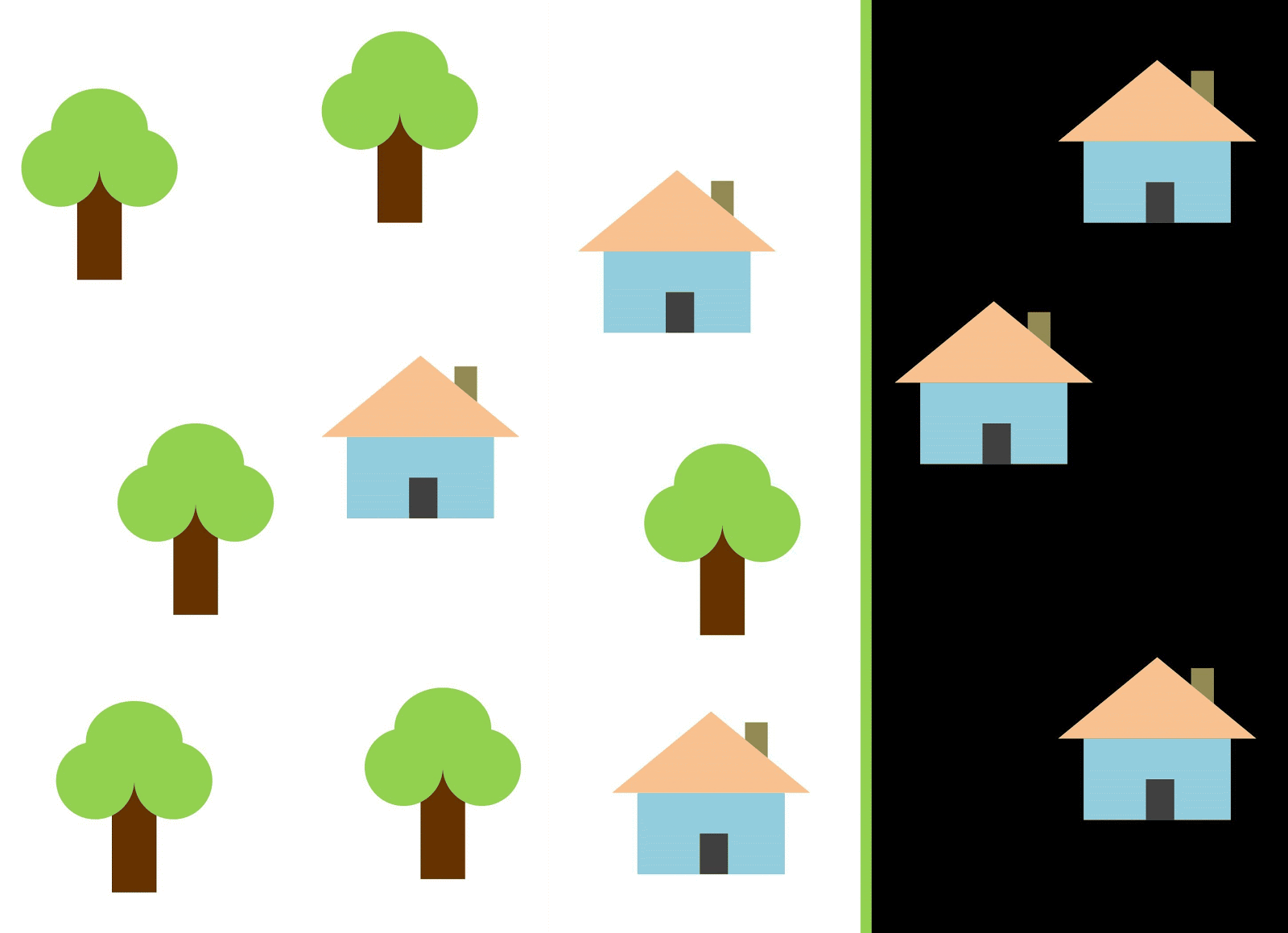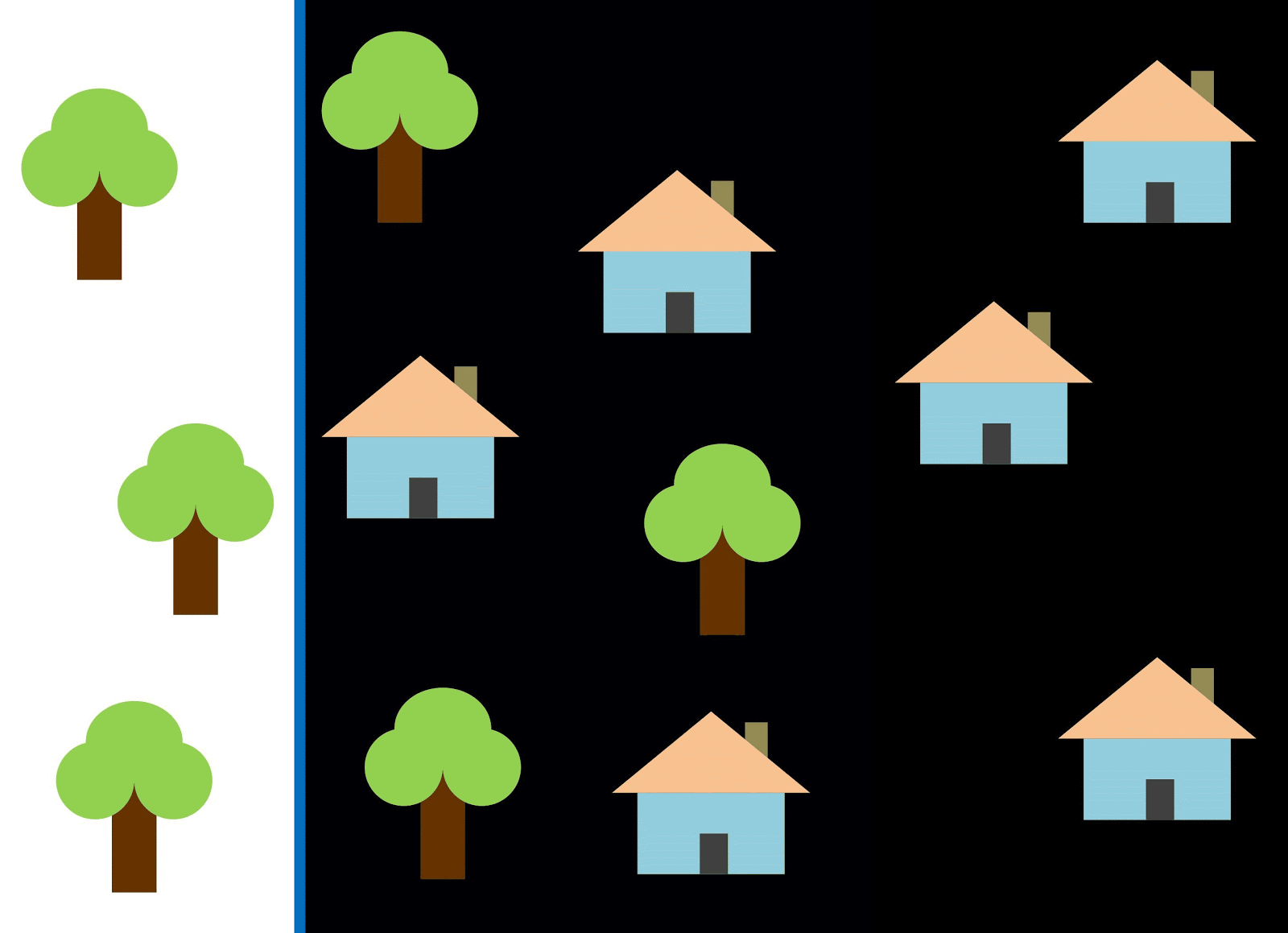
Verwenden wir die rote Linie, um die beiden Klassen zu trennen. In diesem Fall identifizierte der Klassifizierer die meisten Häuser, aber ein Haus wurde nicht seiner Klasse zugeordnet, und drei weitere Bäume wurden fälschlicherweise den "Häusern" zugeordnet. Um kein einziges Haus zu verpassen, können Sie den Klassifikator in Form einer blauen Linie verwenden. Dann wird zu Hause alles abgedeckt, dh wir sagen, dass die Rückrufmetrik (Fülle) hoch ist. Es stellte sich jedoch heraus, dass nicht alle klassifizierten Werte Häuser waren, dh gleichzeitig erhielten wir einen niedrigen Wert der Präzisionsmetrik. Wenn wir die grüne Linie verwenden, sind alle als Häuser klassifizierten Bilder tatsächlich Häuser, dh der Klassifikator zeigt eine hohe Genauigkeit. In diesem Fall ist die Fülle geringer, da die drei Häuser nicht berücksichtigt werden. In den meisten Fällen müssen wir einen Kompromiss zwischen Genauigkeit und Vollständigkeit finden.
Dieses Problem von Häusern und Bäumen ähnelt dem Problem von Gebäuden, unbebauten Grundstücken und Gruben. Die Priorität der Klassifizierungsmetriken für Satellitenbilder kann je nach Aufgabe variieren. Wenn Sie beispielsweise sicherstellen müssen, dass alle bebauten Gebiete ausnahmslos als Gebäude klassifiziert sind und Sie bereit sind, Pixel anderer Klassen mit ähnlichen Signaturen zu akzeptieren, die ebenfalls als Gebäude klassifiziert werden, benötigen Sie ein Modell mit hoher Vollständigkeit. Wenn es für Sie wichtiger ist, ein Gebäude zu klassifizieren, ohne Pixel anderer Klassen hinzuzufügen, und Sie bereit sind, die Klassifizierung gemischter Gebiete aufzugeben, wählen Sie einen Klassifizierer mit hoher Genauigkeit. Bei Häusern und Bäumen verwendet das übliche Modell die rote Linie, um ein Gleichgewicht zwischen Genauigkeit und Vollständigkeit zu gewährleisten.
Verwendete Daten
Als Zeichen werden wir die Werte von sechs Bereichen (Band 2 - Band 7) des Bildes aus Landsat 5 TM verwenden und versuchen, die binäre Entwicklungsklasse vorherzusagen. Für Schulungen und Tests werden multispektrale Daten (Bilder und eine Ebene mit einer binären Gebäudeklasse) mit Landsat 5 für 2011 für Bangalore verwendet. Und für die Vorhersage werden multispektrale Landsat 5-Daten verwendet, die 2005 in Hyderabad erhalten wurden.
Da wir für den Unterricht markierte Daten verwenden, wird dies als Unterricht mit dem Lehrer bezeichnet.
Multispektrale Trainingsdaten und die entsprechende binäre Schicht mit Entwicklung.Um ein neuronales Netzwerk zu erstellen, verwenden wir Python - die Google Tensorflow-Bibliothek. Wir werden auch diese Bibliotheken brauchen:
- pyrsgis - zum Lesen und Schreiben von GeoTIFF.
- scikit-learn - zur Datenvorverarbeitung und Genauigkeitsbewertung.
- numpy - für grundlegende Operationen mit Arrays.
Und jetzt schreiben wir ohne weiteres den Code.
Legen Sie alle drei Dateien in einem Verzeichnis ab, schreiben Sie den Pfad und die Namen der Eingabedateien in das Skript und lesen Sie dann die GeoTIFF-Dateien.
import os from pyrsgis import raster os.chdir("E:\\yourDirectoryName") mxBangalore = 'l5_Bangalore2011_raw.tif' builtupBangalore = 'l5_Bangalore2011_builtup.tif' mxHyderabad = 'l5_Hyderabad2011_raw.tif'
Das
raster Modul aus dem
pyrsgis Paket liest GeoTIFF-
pyrsgis und DN-Werte (Digital Number) als separate NumPy-Arrays. Wenn Sie an Details interessiert sind, lesen Sie
hier .
Jetzt zeigen wir die Größe der gelesenen Daten an.
print("Bangalore multispectral image shape: ", featuresBangalore.shape) print("Bangalore binary built-up image shape: ", labelBangalore.shape) print("Hyderabad multispectral image shape: ", featuresHyderabad.shape)
Ergebnis:
Bangalore multispectral image shape: 6, 2054, 2044 Bangalore binary built-up image shape: 2054, 2044 Hyderabad multispectral image shape: 6, 1318, 1056
Wie Sie sehen können, haben die Bilder von Bangalore die gleiche Anzahl von Zeilen und Spalten wie in der Binärebene (entsprechend dem Gebäude). Die Anzahl der Schichten in multispektralen Bildern in Bangalore und Hyderabad stimmt ebenfalls überein. Das Modell lernt anhand der entsprechenden Werte für alle 6 Spektren zu entscheiden, welche Pixel zum Gebäude gehören und welche nicht. Daher müssen multispektrale Bilder dieselbe Anzahl von Merkmalen (Bereichen) aufweisen, die in derselben Reihenfolge aufgeführt sind.
Jetzt verwandeln wir die Arrays in zweidimensionale Arrays, wobei jede Zeile ein separates Pixel darstellt, da dies für den Betrieb der meisten Algorithmen für maschinelles Lernen erforderlich ist. Wir werden dies mit dem
convert aus dem
pyrsgis Paket
pyrsgis .
Datenumstrukturierungsschema. from pyrsgis.convert import changeDimension featuresBangalore = changeDimension(featuresBangalore) labelBangalore = changeDimension (labelBangalore) featuresHyderabad = changeDimension(featuresHyderabad) nBands = featuresBangalore.shape[1] labelBangalore = (labelBangalore == 1).astype(int) print("Bangalore multispectral image shape: ", featuresBangalore.shape) print("Bangalore binary built-up image shape: ", labelBangalore.shape) print("Hyderabad multispectral image shape: ", featuresHyderabad.shape)
Ergebnis:
Bangalore multispectral image shape: 4198376, 6 Bangalore binary built-up image shape: 4198376 Hyderabad multispectral image shape: 1391808, 6
In der siebten Zeile haben wir alle Pixel mit dem Wert 1 extrahiert. Dies hilft, Probleme mit Pixeln ohne Informationen (NoData) zu vermeiden, die häufig extrem hohe oder niedrige Werte aufweisen.
Jetzt werden wir die Daten in Trainings- und Validierungsbeispiele aufteilen. Dies ist erforderlich, damit das Modell die Testdaten nicht sieht und mit den neuen Informationen genauso gut funktioniert. Andernfalls wird das Modell umgeschult und funktioniert nur mit Trainingsdaten.
from sklearn.model_selection import train_test_split xTrain, xTest, yTrain, yTest = train_test_split(featuresBangalore, labelBangalore, test_size=0.4, random_state=42) print(xTrain.shape) print(yTrain.shape) print(xTest.shape) print(yTest.shape)
Ergebnis:
(2519025, 6) (2519025,) (1679351, 6) (1679351,) test_size=0.4
bedeutet, dass die Daten in einem Verhältnis von 60/40 in Training und Validierung unterteilt sind.
Viele Algorithmen für maschinelles Lernen, einschließlich neuronaler Netze, benötigen normalisierte Daten. Dies bedeutet, dass sie innerhalb eines bestimmten Bereichs (in diesem Fall von 0 bis 1) verteilt werden müssen. Um diese Anforderung zu erfüllen, normalisieren wir daher die Symptome. Dies kann erreicht werden, indem der Minimalwert extrahiert und dann durch den Spread dividiert wird (die Differenz zwischen den Maximal- und Minimalwerten). Da der Landsat-Datensatz 8-Bit ist, sind die Minimal- und Maximalwerte 0 und 255 (2
⁸ = 256 Werte).
Beachten Sie, dass es für die Normalisierung immer besser ist, die Minimal- und Maximalwerte basierend auf den Daten zu berechnen. Um die Aufgabe zu vereinfachen, halten wir uns standardmäßig an den 8-Bit-Bereich.
Eine weitere Stufe der Vorverarbeitung ist die Transformation der Attributmatrix von zweidimensional zu dreidimensional, sodass das Modell jede Zeile als separates Pixel (separates Lernobjekt) wahrnimmt.
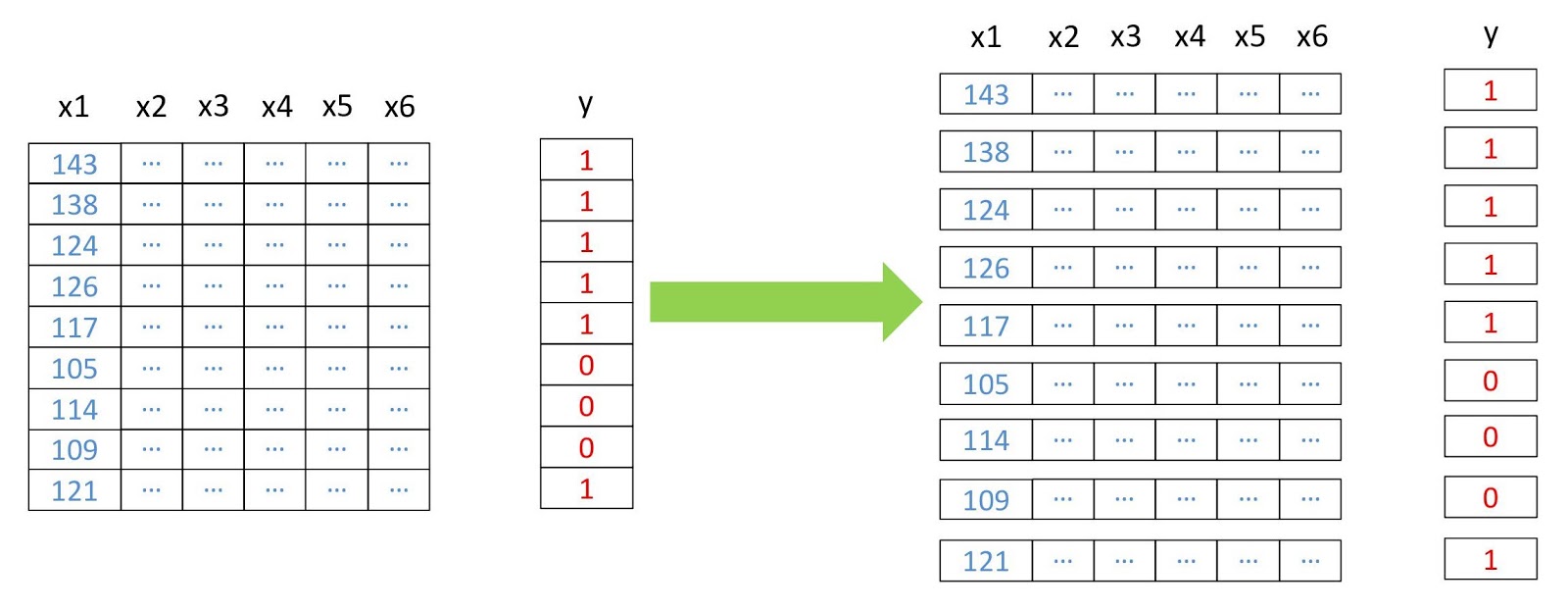
Ergebnis:
(2519025, 1, 6) (1679351, 1, 6) (1391808, 1, 6)
Alles ist fertig, lassen Sie uns unser Modell mit
Keras zusammenbauen . Verwenden Sie zunächst das sequentielle Modell und fügen Sie nacheinander Ebenen hinzu. Wir werden eine Eingabeebene haben, deren Anzahl der Knoten der Anzahl der Bereiche (
nBands ) entspricht - in unserem Fall sind es 6. Wir werden auch eine versteckte Ebene mit 14 Knoten und der
ReLu Aktivierungsfunktion
ReLu . Die letzte Schicht besteht aus zwei Knoten zum Definieren einer binären Gebäudeklasse mit der
softmax Aktivierungsfunktion, die zum Anzeigen eines kategorisierten Ergebnisses geeignet ist. Lesen Sie hier mehr über Aktivierungsfunktionen.
from tensorflow import keras
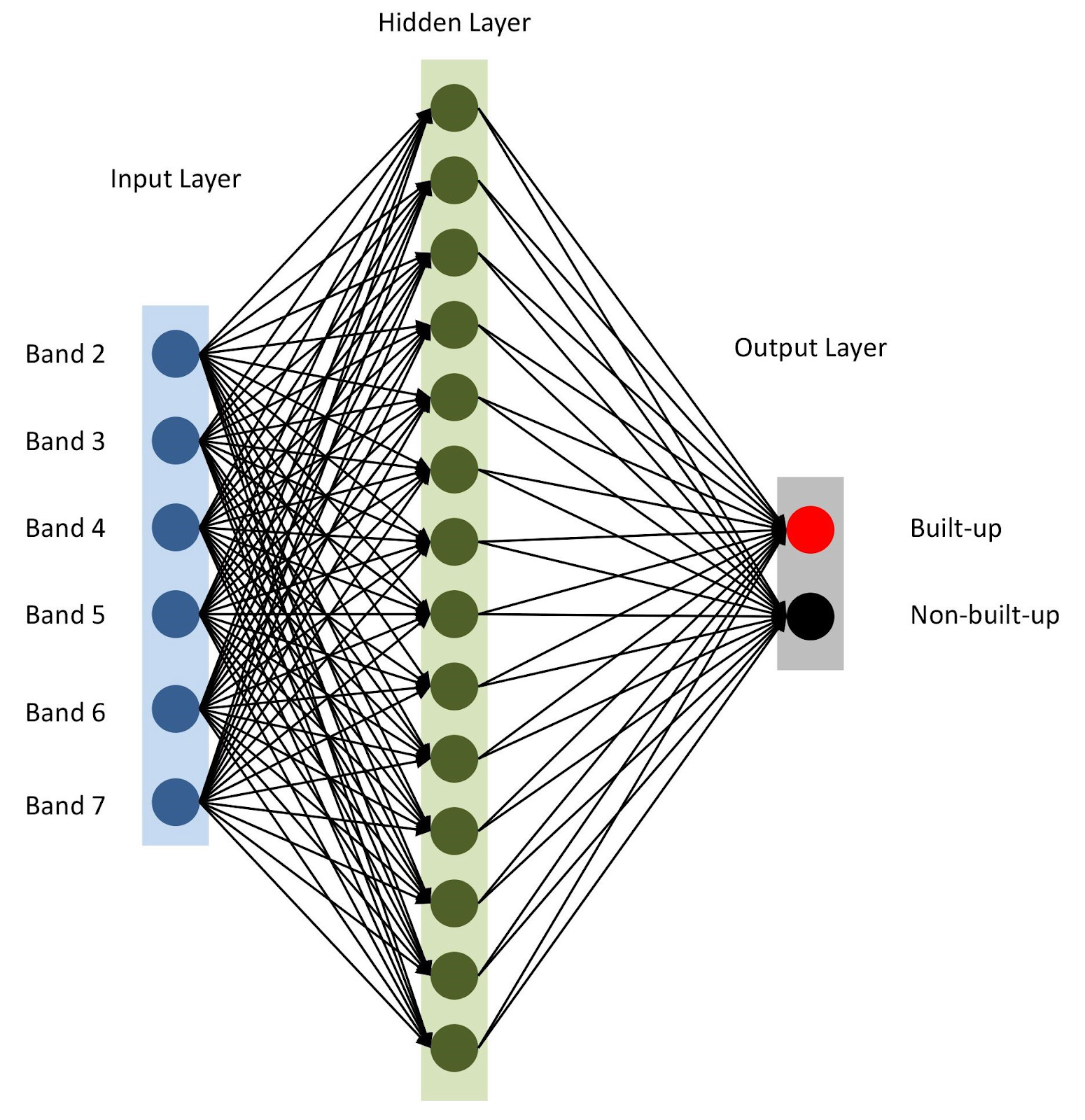Neuronale NetzwerkarchitekturWie in Zeile 10 erwähnt, geben wir
adam als Modelloptimierer an (es gibt mehrere
andere ). In diesem Fall verwenden wir die Kreuzentropie als Verlustfunktion (en.
categorical-sparse-crossentropy - mehr dazu finden Sie
hier ). Um die Qualität des Modells zu beurteilen, verwenden wir die
accuracy .
Schließlich werden wir beginnen, unser Modell für zwei Epochen (oder Iterationen) auf
xTrain und
yTrain . Dies kann je nach Datengröße und Verarbeitungsleistung einige Zeit dauern. Folgendes sehen Sie nach der Kompilierung:
Lassen Sie uns die Werte für die Validierungsdaten vorhersagen, die wir separat speichern, und verschiedene Genauigkeitsmetriken berechnen.
from sklearn.metrics import confusion_matrix, precision_score, recall_score
Die
softmax Funktion generiert separate Spalten für Wahrscheinlichkeitswerte für jede Klasse. Wir verwenden nur die Werte für die erste Klasse ("es gibt ein Gebäude"), wie aus der sechsten Zeile des obigen Codes ersichtlich ist. Die Bewertung der Arbeit von Geodatenanalysemodellen ist im Gegensatz zu anderen klassischen Problemen des maschinellen Lernens nicht so einfach. Es ist unfair, sich auf einen allgemeinen Gesamtfehler zu verlassen. Der Schlüssel zu einem erfolgreichen Modell ist die räumliche Anordnung. Somit können die Verwirrungsmatrix, Genauigkeit und Vollständigkeit eine korrektere Vorstellung von der Qualität des Modells geben.
Die Konsole zeigt also die Fehlermatrix, Genauigkeit und Vollständigkeit an.Wie Sie der Verwirrungsmatrix entnehmen können, gibt es Tausende von Pixeln, die sich auf Gebäude beziehen, aber unterschiedlich klassifiziert sind und umgekehrt. Ihr Anteil am gesamten Datenvolumen ist jedoch nicht zu groß. Die Genauigkeit und Vollständigkeit der Testdaten hat den Schwellenwert von 0,8 überschritten.
Sie können mehr Zeit aufwenden und mehrere Iterationen durchführen, um die optimale Anzahl versteckter Ebenen, die Anzahl der Knoten in jeder verborgenen Ebene sowie die Anzahl der Epochen zu ermitteln, um die gewünschte Genauigkeit zu erzielen. Bei Bedarf können Fernerkundungsindizes wie NDBI oder NDWI als Funktionen verwendet werden. Wenn Sie die gewünschte Genauigkeit erreicht haben, verwenden Sie das Modell, um die Entwicklung basierend auf neuen Daten vorherzusagen und das Ergebnis in GeoTIFF zu exportieren. Für solche Aufgaben können Sie ein ähnliches Modell mit geringfügigen Änderungen verwenden.
predicted = model.predict(feature2005) predicted = predicted[:,1]
Bitte beachten Sie, dass wir GeoTIFF mit vorhergesagten Wahrscheinlichkeitswerten und nicht mit ihrer binärisierten Version exportieren. Später in der GIS-Umgebung können wir den Schwellenwert für eine Ebene vom Typ float festlegen, wie in der folgenden Abbildung dargestellt.
Vom Modell auf der Grundlage multispektraler Daten vorhergesagte Hyderabad-Aufbauschicht.Die Modellgenauigkeit wurde bereits mit Präzision und Rückruf gemessen. Sie können auch herkömmliche Überprüfungen (z. B. mithilfe des Kappa-Koeffizienten) für eine neue vorhergesagte Ebene durchführen. Zusätzlich zu den oben genannten Schwierigkeiten bei der Klassifizierung von Satellitenbildern umfassen andere offensichtliche Einschränkungen die Unmöglichkeit der Vorhersage auf der Grundlage von Bildern, die zu verschiedenen Jahreszeiten und in verschiedenen Regionen aufgenommen wurden, da sie unterschiedliche spektrale Signaturen aufweisen.
Das in diesem Artikel beschriebene Modell hat die einfachste Architektur für neuronale Netze. Bessere Ergebnisse können mit komplexeren Modellen erzielt werden, einschließlich Faltungs-Neuronalen Netzen. Der Hauptvorteil einer solchen Klassifizierung ist ihre Skalierbarkeit (Anwendbarkeit) nach dem Training des Modells.
Die verwendeten Daten und der gesamte Code sind
hier .