Mein Name ist Vyacheslav, ich bin ein chronischer Mathematiker und seit einigen Jahren habe ich keine Zyklen mehr verwendet, wenn ich mit Arrays gearbeitet habe ...
Genau seit ich Vektoroperationen in NumPy entdeckt habe. Ich möchte Ihnen die NumPy-Funktionen vorstellen, mit denen ich am häufigsten Arrays von Daten und Bildern verarbeite. Am Ende des Artikels werde ich zeigen, wie Sie das NumPy-Toolkit verwenden können, um Bilder ohne Iterationen zu falten (= sehr schnell).
Vergiss nicht
import numpy as np
und lass uns gehen!
Inhalt
Was ist numpy?Array-ErstellungZugriff auf Elemente, SlicesDie Form des Arrays und seine ÄnderungAchsenumlagerung und TranspositionArray-JoinKlonen von DatenMathematische Operationen an Array-ElementenMatrixmultiplikationAggregatorenAnstelle einer Schlussfolgerung - ein BeispielWas ist numpy?
Dies ist eine Open Source-Bibliothek, die sich einmal vom SciPy-Projekt getrennt hat. NumPy ist der Nachkomme von Numeric und NumArray. NumPy basiert auf der LAPAC-Bibliothek, die in Fortran geschrieben ist. Eine Nicht-Python-Alternative für NumPy ist Matlab.
Aufgrund der Tatsache, dass NumPy auf Fortran basiert, ist es eine schnelle Bibliothek. Und aufgrund der Tatsache, dass es Vektoroperationen mit mehrdimensionalen Arrays unterstützt, ist es äußerst praktisch.
Zusätzlich zur Basisversion (mehrdimensionale Arrays in der Basisversion) enthält NumPy eine Reihe von Paketen zur Lösung spezieller Aufgaben, zum Beispiel:
- numpy.linalg - implementiert Operationen der linearen Algebra (eine einfache Multiplikation von Vektoren und Matrizen ist in der Basisversion enthalten);
- numpy.random - implementiert Funktionen zum Arbeiten mit Zufallsvariablen;
- numpy.fft - implementiert die direkte und inverse Fourier-Transformation.
Daher schlage ich vor, nur einige NumPy-Funktionen und Beispiele für deren Verwendung im Detail zu betrachten, damit Sie verstehen, wie leistungsfähig dieses Tool ist!
<up>Array-Erstellung
Es gibt verschiedene Möglichkeiten, ein Array zu erstellen:
- Liste in Array konvertieren:
A = np.array([[1, 2, 3], [4, 5, 6]]) A Out: array([[1, 2, 3], [4, 5, 6]])
- Kopieren Sie das Array (Kopie und Deep Copy erforderlich !!!):
B = A.copy() B Out: array([[1, 2, 3], [4, 5, 6]])
- Erstellen Sie ein Null- oder Ein-Array einer bestimmten Größe:
A = np.zeros((2, 3)) A Out: array([[0., 0., 0.], [0., 0., 0.]])
B = np.ones((3, 2)) B Out: array([[1., 1.], [1., 1.], [1., 1.]])
Oder nehmen Sie die Dimensionen eines vorhandenen Arrays:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.zeros_like(A) B Out: array([[0, 0, 0], [0, 0, 0]])
A = np.array([[1, 2, 3], [4, 5, 6]]) B = np.ones_like(A) B Out: array([[1, 1, 1], [1, 1, 1]])
- Wenn Sie ein zweidimensionales quadratisches Array erstellen, können Sie es zu einer Einheitsdiagonalmatrix machen:
A = np.eye(3) A Out: array([[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]])
- Erstellen Sie mit Schritt Schritt ein Array von Zahlen von Von (einschließlich) bis Bis (nicht einschließlich):
From = 2.5 To = 7 Step = 0.5 A = np.arange(From, To, Step) A Out: array([2.5, 3. , 3.5, 4. , 4.5, 5. , 5.5, 6. , 6.5])
Standardmäßig ist ab = 0, Schritt = 1, sodass eine Variante mit einem Parameter als An interpretiert wird:
A = np.arange(5) A Out: array([0, 1, 2, 3, 4])
Oder mit zwei - wie Von und Bis:
A = np.arange(10, 15) A Out: array([10, 11, 12, 13, 14])
Beachten Sie, dass in Methode Nr. 3 die Abmessungen des Arrays als
ein Parameter (ein Tupel von Größen) übergeben wurden. Mit dem zweiten Parameter in den Methoden Nr. 3 und Nr. 4 können Sie den gewünschten Typ von Array-Elementen angeben:
A = np.zeros((2, 3), 'int') A Out: array([[0, 0, 0], [0, 0, 0]])
B = np.ones((3, 2), 'complex') B Out: array([[1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j], [1.+0.j, 1.+0.j]])
Mit der Astype-Methode können Sie das Array in einen anderen Typ umwandeln. Der gewünschte Typ wird als Parameter angegeben:
A = np.ones((3, 2)) B = A.astype('str') B Out: array([['1.0', '1.0'], ['1.0', '1.0'], ['1.0', '1.0']], dtype='<U32')
Alle verfügbaren Typen finden Sie im sctypes-Wörterbuch:
np.sctypes Out: {'int': [numpy.int8, numpy.int16, numpy.int32, numpy.int64], 'uint': [numpy.uint8, numpy.uint16, numpy.uint32, numpy.uint64], 'float': [numpy.float16, numpy.float32, numpy.float64, numpy.float128], 'complex': [numpy.complex64, numpy.complex128, numpy.complex256], 'others': [bool, object, bytes, str, numpy.void]}
<up>Zugriff auf Elemente, Slices
Der Zugriff auf die Elemente des Arrays erfolgt über ganzzahlige Indizes. Der Countdown beginnt bei 0:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, 1] Out: 5
Wenn Sie sich ein mehrdimensionales Array als ein System verschachtelter eindimensionaler Arrays vorstellen (ein lineares Array, dessen Elemente lineare Arrays sein können), wird deutlich, dass Sie mit einem unvollständigen Satz von Indizes auf Subarrays zugreifen können:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1] Out: array([4, 5, 6])
Angesichts dieses Paradigmas können wir das Beispiel des Zugriffs auf ein Element umschreiben:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1][1] Out: 5
Bei Verwendung eines unvollständigen Satzes von Indizes werden die fehlenden Indizes implizit durch eine Liste aller möglichen Indizes entlang der entsprechenden Achse ersetzt. Sie können dies explizit tun, indem Sie ":" setzen. Das vorherige Beispiel mit einem Index kann wie folgt umgeschrieben werden:
A = np.array([[1, 2, 3], [4, 5, 6]]) A[1, :] Out: array([4, 5, 6])
Sie können einen Index entlang einer beliebigen Achse oder Achsen überspringen. Wenn auf die Achse Achsen mit Indexierung folgen, muss ":":
A = np.array([[1, 2, 3], [4, 5, 6]]) A[:, 1] Out: array([2, 5])
Indizes können negative ganzzahlige Werte annehmen. In diesem Fall ist die Anzahl vom Ende des Arrays:
A = np.arange(5) print(A) A[-1] Out: [0 1 2 3 4] 4
Sie können nicht einzelne Indizes verwenden, sondern Listen von Indizes entlang jeder Achse:
A = np.arange(5) print(A) A[[0, 1, -1]] Out: [0 1 2 3 4] array([0, 1, 4])
Oder Indexbereiche in Form von "Von: Bis: Schritt". Dieser Entwurf wird eine Scheibe genannt. Alle Elemente werden gemäß der Liste der Indizes ausgewählt, beginnend vom From-Index einschließlich bis zum To-Index, der im Schritt Schritt nicht enthalten ist:
A = np.arange(5) print(A) A[0:4:2] Out: [0 1 2 3 4] array([0, 2])
Der Indexschritt hat den Standardwert 1 und kann übersprungen werden:
A = np.arange(5) print(A) A[0:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])
Die Werte Von und Bis haben auch Standardwerte: 0 und die Größe des Arrays entlang der Indexachse:
A = np.arange(5) print(A) A[:4] Out: [0 1 2 3 4] array([0, 1, 2, 3])
A = np.arange(5) print(A) A[-3:] Out: [0 1 2 3 4] array([2, 3, 4])
Wenn Sie standardmäßig Von und Bis verwenden möchten (alle Indizes auf dieser Achse) und der Schritt von 1 abweicht, müssen Sie zwei Doppelpunktpaare verwenden, damit der Interpreter einen einzelnen Parameter als Schritt identifizieren kann. Der folgende Code "erweitert" das Array entlang der zweiten Achse, ändert sich jedoch nicht entlang der ersten:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]
Jetzt lass es uns tun
print(A) B[0, 0] = 0 print(A) Out: [[1 2 3] [4 5 6]] [[1 2 0] [4 5 6]]
Wie Sie sehen können, haben wir durch B die Daten in A geändert. Deshalb ist es wichtig, Kopien in realen Aufgaben zu verwenden. Das obige Beispiel sollte folgendermaßen aussehen:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.copy()[:, ::-1] print("A", A) print("B", B) Out: A [[1 2 3] [4 5 6]] B [[3 2 1] [6 5 4]]
NumPy bietet auch die Möglichkeit, über ein boolesches Indexarray auf mehrere Array-Elemente zuzugreifen. Das Indexarray muss mit der Form des indizierten Arrays übereinstimmen.
A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] Out: array([3, 4, 6])
Wie Sie sehen können, gibt eine solche Konstruktion ein flaches Array zurück, das aus Elementen des indizierten Arrays besteht, die echten Indizes entsprechen. Wenn wir jedoch einen solchen Zugriff auf die Elemente des Arrays verwenden, um deren Werte zu ändern, bleibt die Form des Arrays erhalten:
A = np.array([[1, 2, 3], [4, 5, 6]]) I = np.array([[False, False, True], [ True, False, True]]) A[I] = 0 print(A) Out: [[1 2 0] [0 5 0]]
Logische Operationen logisch_und, logisch_oder und logisch_nicht werden über die Indizierung von Booleschen Arrays definiert und führen logische Operationen AND, OR und NOT elementweise aus:
A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) B = A.copy() C = A.copy() D = A.copy() B[np.logical_and(I1, I2)] = 0 C[np.logical_or(I1, I2)] = 0 D[np.logical_not(I1)] = 0 print('B\n', B) print('\nC\n', C) print('\nD\n', D) Out: B [[1 2 3] [4 5 0]] C [[1 0 0] [0 5 0]] D [[0 0 3] [4 0 6]]
logisch_und und logisch_oder nehmen 2 Operanden, logisch_nicht einen. Sie können die Operatoren &, | verwenden und ~, um AND, OR bzw. NOT mit einer beliebigen Anzahl von Operanden auszuführen:
A = np.array([[1, 2, 3], [4, 5, 6]]) I1 = np.array([[False, False, True], [True, False, True]]) I2 = np.array([[False, True, False], [False, False, True]]) A[I1 & (I1 | ~ I2)] = 0 print(A) Out: [[1 2 0] [0 5 0]]
Das entspricht der Verwendung von nur I1.
Es ist möglich, ein logisches Indexarray zu erhalten, das in seiner Form einem Array von Werten entspricht, indem eine logische Bedingung mit dem Namen des Arrays als Operand geschrieben wird. Der boolesche Wert des Index wird als die Wahrheit des Ausdrucks für das entsprechende Array-Element berechnet.
Suchen Sie ein Indexarray von I-Elementen, die größer als 3 sind, und Elemente mit Werten von weniger als 2 und mehr als 4 - werden auf Null zurückgesetzt:
A = np.array([[1, 2, 3], [4, 5, 6]]) print('A before\n', A) I = A > 3 print('I\n', I) A[np.logical_or(A < 2, A > 4)] = 0 print('A after\n', A) Out: A before [[1 2 3] [4 5 6]] I [[False False False] [ True True True]] A after [[0 2 3] [4 0 0]]
<up>Die Form des Arrays und seine Änderung
Ein mehrdimensionales Array kann als eindimensionales Array maximaler Länge dargestellt, entlang der Länge der allerletzten Achse in Fragmente geschnitten und beginnend mit letzterer in Schichten entlang der Achsen gelegt werden.
Betrachten Sie zur Verdeutlichung ein Beispiel:
A = np.arange(24) B = A.reshape(4, 6) C = A.reshape(4, 3, 2) print('B\n', B) print('\nC\n', C) Out: B [[ 0 1 2 3 4 5] [ 6 7 8 9 10 11] [12 13 14 15 16 17] [18 19 20 21 22 23]] C [[[ 0 1] [ 2 3] [ 4 5]] [[ 6 7] [ 8 9] [10 11]] [[12 13] [14 15] [16 17]] [[18 19] [20 21] [22 23]]]
In diesem Beispiel haben wir zwei neue Arrays aus einem eindimensionalen Array mit einer Länge von 24 Elementen gebildet. Array B, Größe 4 x 6. Wenn Sie sich die Reihenfolge der Werte ansehen, sehen Sie, dass sich entlang der zweiten Dimension Ketten aufeinanderfolgender Werte befinden.
In Array C, 4 mal 3 mal 2, verlaufen kontinuierliche Werte entlang der letzten Achse. Entlang der zweiten Achse befinden sich Blöcke in Reihe, deren Kombination zu einer Reihe entlang der zweiten Achse des Arrays B führen würde.
Und da wir keine Kopien erstellt haben, wird deutlich, dass es sich um unterschiedliche Darstellungsformen desselben Datenarrays handelt. Daher können Sie die Form des Arrays einfach und schnell ändern, ohne die Daten selbst zu ändern.
Um die Dimension des Arrays (Anzahl der Achsen) herauszufinden, können Sie das Feld ndim (Anzahl) verwenden und die Größe entlang jeder Achsenform (Tupel) ermitteln. Die Bemaßung kann auch an der Länge der Form erkannt werden. Um die Gesamtzahl der Elemente in einem Array zu ermitteln, können Sie den Größenwert verwenden:
A = np.arange(24) C = A.reshape(4, 3, 2) print(C.ndim, C.shape, len(C.shape), A.size) Out: 3 (4, 3, 2) 3 24
Beachten Sie, dass ndim und shape Attribute sind, keine Methoden!
Um das Array eindimensional anzuzeigen, können Sie die Ravel-Funktion verwenden:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.ravel() Out: array([1, 2, 3, 4, 5, 6])
Verwenden Sie die Umformungsmethode, um die Größe entlang der Achsen oder Bemaßungen zu ändern:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 2) Out: array([[1, 2], [3, 4], [5, 6]])
Es ist wichtig, dass die Anzahl der Elemente erhalten bleibt. Andernfalls tritt ein Fehler auf:
A = np.array([[1, 2, 3], [4, 5, 6]]) A.reshape(3, 3) Out: ValueError Traceback (most recent call last) <ipython-input-73-d204e18427d9> in <module> 1 A = np.array([[1, 2, 3], [4, 5, 6]]) ----> 2 A.reshape(3, 3) ValueError: cannot reshape array of size 6 into shape (3,3)
Da die Anzahl der Elemente konstant ist, kann die Größe entlang einer beliebigen Achse beim Umformen aus den Längenwerten entlang anderer Achsen berechnet werden. Die Größe entlang einer Achse kann mit -1 bezeichnet werden und wird dann automatisch berechnet:
A = np.arange(24) B = A.reshape(4, -1) C = A.reshape(4, -1, 2) print(B.shape, C.shape) Out: (4, 6) (4, 3, 2)
Sie können Reshape anstelle von Ravel verwenden:
A = np.array([[1, 2, 3], [4, 5, 6]]) B = A.reshape(-1) print(B.shape) Out: (6,)
Betrachten Sie die praktische Anwendung einiger Funktionen für die Bildverarbeitung. Als Forschungsgegenstand verwenden wir ein Foto:
Versuchen wir, es mit Python herunterzuladen und zu visualisieren. Dafür benötigen wir OpenCV und Matplotlib:
import cv2 from matplotlib import pyplot as plt I = cv2.imread('sarajevo.jpg')[:, :, ::-1] plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I) plt.show()
Das Ergebnis wird folgendermaßen aussehen:
Beachten Sie die Download-Leiste:
I = cv2.imread('sarajevo.jpg')[:, :, ::-1] print(I.shape) Out: (1280, 1920, 3)
OpenCV arbeitet mit Bildern im BGR-Format, und wir sind mit RGB vertraut. Wir ändern die Bytereihenfolge entlang der Farbachse, ohne mit dem Konstrukt auf die OpenCV-Funktionen zuzugreifen
"[:,:, :: :: 1]".
Reduzieren Sie das Bild auf jeder Achse um das Zweifache. Unser Bild hat gleichmäßige Abmessungen entlang der Achsen, die ohne Interpolation reduziert werden können:
I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) print(I_.shape) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_[:, 0, :, 0]) plt.show()
Wenn wir die Form des Arrays ändern, erhalten wir 2 neue Achsen mit jeweils 2 Werten. Sie entsprechen Frames, die aus ungeraden und geraden Zeilen und Spalten des Originalbilds bestehen.
Eine schlechte Qualität ist auf die Verwendung von Matplotlib zurückzuführen, da dort die axialen Abmessungen sichtbar sind. In der Tat ist die Qualität der Miniaturansicht:
<up>Achsenumlagerung und Transposition
Zusätzlich zum Ändern der Form des Arrays mit derselben Reihenfolge von Dateneinheiten ist es häufig erforderlich, die Reihenfolge der Achsen zu ändern, was natürlich eine Permutation der Datenblöcke zur Folge hat.
Ein Beispiel für eine solche Transformation ist die Transposition einer Matrix: Vertauschen von Zeilen und Spalten.
A = np.array([[1, 2, 3], [4, 5, 6]]) print('A\n', A) print('\nA data\n', A.ravel()) B = AT print('\nB\n', B) print('\nB data\n', B.ravel()) Out: A [[1 2 3] [4 5 6]] A data [1 2 3 4 5 6] B [[1 4] [2 5] [3 6]] B data [1 4 2 5 3 6]
In diesem Beispiel wurde das AT-Konstrukt verwendet, um die Matrix A zu transponieren. Der Transponierungsoperator invertiert die Achsenreihenfolge. Betrachten Sie ein weiteres Beispiel mit drei Achsen:
C = np.arange(24).reshape(4, -1, 2) print(C.shape, np.transpose(C).shape) print() print(C[0]) print() print(CT[:, :, 0]) Out: [[0 1] [2 3] [4 5]] [[0 2 4] [1 3 5]]
Dieser kurze Eintrag hat ein längeres Gegenstück: np.transpose (A). Dies ist ein vielseitigeres Werkzeug zum Ersetzen der Achsenreihenfolge. Mit dem zweiten Parameter können Sie ein Tupel von Achsnummern des Quellarrays angeben, das die Reihenfolge ihrer Position im resultierenden Array bestimmt.
Ordnen Sie beispielsweise die ersten beiden Achsen des Bildes neu an. Das Bild sollte umdrehen, aber die Farbachse unverändert lassen:
I_ = np.transpose(I, (1, 0, 2)) plt.figure(num=None, figsize=(15, 15), dpi=80, facecolor='w', edgecolor='k') plt.imshow(I_) plt.show()
In diesem Beispiel könnte ein anderes Swapaxes-Tool verwendet werden. Diese Methode vertauscht die beiden in den Parametern angegebenen Achsen. Das obige Beispiel könnte folgendermaßen implementiert werden:
I_ = np.swapaxes(I, 0, 1)
<up>Array-Join
Zusammengeführte Arrays müssen dieselbe Anzahl von Achsen haben. Arrays können mit der Bildung einer neuen Achse oder entlang einer vorhandenen Achse kombiniert werden.
Um mit der Bildung einer neuen Achse kombiniert zu werden, müssen die ursprünglichen Arrays entlang aller Achsen die gleichen Abmessungen haben:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) print(D.shape) D Out: (3, 2, 4) array([[[1, 2, 3, 4], [5, 6, 7, 8]], [[5, 6, 7, 8], [1, 2, 3, 4]], [[4, 3, 2, 1], [8, 7, 6, 5]]])
Wie Sie dem Beispiel entnehmen können, wurden die Operandenarrays zu Unterarrays des neuen Objekts und wurden entlang der neuen Achse ausgerichtet, die die allererste in der Reihenfolge ist.
Um Arrays entlang einer vorhandenen Achse zu kombinieren, müssen sie auf allen Achsen dieselbe Größe haben, mit Ausnahme derjenigen, die zum Verbinden ausgewählt wurde, und sie können entlang dieser Achse beliebige Größen haben:
A = np.ones((2, 1, 2)) B = np.zeros((2, 3, 2)) C = np.concatenate((A, B), 1) print(C.shape) C Out: (2, 4, 2) array([[[1., 1.], [0., 0.], [0., 0.], [0., 0.]], [[1., 1.], [0., 0.], [0., 0.], [0., 0.]]])
Zum Kombinieren entlang der ersten oder zweiten Achse können Sie die Methoden vstack bzw. hstack verwenden. Wir zeigen dies anhand eines Beispiels von Bildern. vstack kombiniert Bilder mit derselben Breite in der Höhe und hsstack kombiniert Bilder mit derselben Höhe in einer Breite:
I = cv2.imread('sarajevo.jpg')[:, :, ::-1] I_ = I.reshape(I.shape[0] // 2, 2, I.shape[1] // 2, 2, -1) Ih = np.hstack((I_[:, 0, :, 0], I_[:, 0, :, 1])) Iv = np.vstack((I_[:, 0, :, 0], I_[:, 1, :, 0])) plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Ih) plt.show() plt.figure(num=None, figsize=(10, 10), dpi=80, facecolor='w', edgecolor='k') plt.imshow(Iv) plt.show()
Bitte beachten Sie, dass in allen Beispielen dieses Abschnitts die verknüpften Arrays von einem Parameter (Tupel) übergeben werden. Die Anzahl der Operanden kann beliebig sein, aber nicht unbedingt nur 2.
Achten Sie beim Kombinieren von Arrays auch darauf, was mit dem Speicher passiert:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = A[::-1] C = A[:, ::-1] D = np.stack((A, B, C)) D[0, 0, 0] = 0 print(A) Out: [[1 2 3 4] [5 6 7 8]]
Da ein neues Objekt erstellt wird, werden die darin enthaltenen Daten aus den ursprünglichen Arrays kopiert, sodass Änderungen an den neuen Daten keine Auswirkungen auf das Original haben.
<up>Klonen von Daten
Der Operator np.repeat (A, n) gibt ein eindimensionales Array mit Elementen des Arrays A zurück, von denen jedes n-mal wiederholt wird.
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) print(np.repeat(A, 2)) Out: [1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8]
Nach dieser Konvertierung können Sie die Geometrie des Arrays neu erstellen und doppelte Daten auf einer Achse erfassen:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1) print(B) Out: [[[1 1] [2 2] [3 3] [4 4]] [[5 5] [6 6] [7 7] [8 8]]]
Diese Option unterscheidet sich von der Kombination des Arrays mit dem Stapeloperator selbst nur an der Position der Achse, entlang der sich dieselben Daten befinden. Im obigen Beispiel ist dies die letzte Achse, wenn Sie den Stapel verwenden - die erste:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.stack((A, A)) print(B) Out: [[[1 2 3 4] [5 6 7 8]] [[1 2 3 4] [5 6 7 8]]]
Unabhängig davon, wie die Daten geklont werden, besteht der nächste Schritt darin, die Achse, entlang der dieselben Werte stehen, an eine beliebige Position mit dem Achsensystem zu verschieben:
A = np.array([[1, 2, 3, 4], [5, 6, 7, 8]]) B = np.transpose(np.stack((A, A)), (1, 0, 2)) C = np.transpose(np.repeat(A, 2).reshape(A.shape[0], A.shape[1], -1), (0, 2, 1)) print('B\n', B) print('\nC\n', C) Out: B [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]] C [[[1 2 3 4] [1 2 3 4]] [[5 6 7 8] [5 6 7 8]]]
Wenn wir eine Achse mithilfe der Wiederholung von Elementen „strecken“ möchten, muss die Achse mit denselben Werten
nach dem Erweiterbaren (mithilfe der Transponierung) platziert und dann diese beiden Achsen (mithilfe der Umformung) kombiniert werden. Betrachten Sie ein Beispiel für das Strecken eines Bildes entlang einer vertikalen Achse durch Duplizieren von Zeilen:
I0 = cv2.imread('sarajevo.jpg')[:, :, ::-1]
<up>Mathematische Operationen an Array-Elementen
Wenn A und B Arrays gleicher Größe sind, können sie addiert, multipliziert, subtrahiert, geteilt und zu einer Potenz erhoben werden. Diese Operationen werden
Element für Element ausgeführt , das resultierende Array stimmt in der Geometrie mit den ursprünglichen Arrays überein, und jedes seiner Elemente ist das Ergebnis der entsprechenden Operation an einem Elementpaar aus den ursprünglichen Arrays:
A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([[1., -2., -3.], [7., 8., 9.], [4., 5., 6.], ]) C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[ 0. 0. 0.] [11. 13. 15.] [11. 13. 15.]] - [[-2. 4. 6.] [-3. -3. -3.] [ 3. 3. 3.]] * [[-1. -4. -9.] [28. 40. 54.] [28. 40. 54.]] / [[-1. -1. -1. ] [ 0.57142857 0.625 0.66666667] [ 1.75 1.6 1.5 ]] ** [[-1.0000000e+00 2.5000000e-01 3.7037037e-02] [ 1.6384000e+04 3.9062500e+05 1.0077696e+07] [ 2.4010000e+03 3.2768000e+04 5.3144100e+05]]
Sie können eine beliebige Operation von oben für das Array und die Nummer ausführen. In diesem Fall wird die Operation auch für jedes der Elemente des Arrays ausgeführt:
A = np.array([[-1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = -2. C = A + B D = A - B E = A * B F = A / B G = A ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-3. 0. 1.] [ 2. 3. 4.] [ 5. 6. 7.]] - [[ 1. 4. 5.] [ 6. 7. 8.] [ 9. 10. 11.]] * [[ 2. -4. -6.] [ -8. -10. -12.] [-14. -16. -18.]] / [[ 0.5 -1. -1.5] [-2. -2.5 -3. ] [-3.5 -4. -4.5]] ** [[1. 0.25 0.11111111] [0.0625 0.04 0.02777778] [0.02040816 0.015625 0.01234568]]
Da ein mehrdimensionales Array als flaches Array (erste Achse) betrachtet werden kann, dessen Elemente Arrays (andere Achsen) sind, ist es möglich, die betrachteten Operationen an den Arrays A und B auszuführen, wenn die Geometrie von B mit der Geometrie der Subarrays von A mit einem festen Wert entlang der ersten Achse übereinstimmt . Mit anderen Worten, mit der gleichen Anzahl von Achsen und Größen A [i] und B. In diesem Fall ist jedes der Arrays A [i] und B Operanden für Operationen, die auf Arrays definiert sind.
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = AT + B D = AT - B E = AT * B F = AT / B G = AT ** B print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 2.8 5.7] [ 0.9 3.8 6.7] [ 1.9 4.8 7.7]] - [[ 2.1 5.2 8.3] [ 3.1 6.2 9.3] [ 4.1 7.2 10.3]] * [[ -1.1 -4.8 -9.1] [ -2.2 -6. -10.4] [ -3.3 -7.2 -11.7]] / [[-0.90909091 -3.33333333 -5.38461538] [-1.81818182 -4.16666667 -6.15384615] [-2.72727273 -5. -6.92307692]] ** [[1. 0.18946457 0.07968426] [0.4665165 0.14495593 0.06698584] [0.29865282 0.11647119 0.05747576]]
In diesem Beispiel wird Array B mit jeder Zeile von Array A operiert. Wenn Sie den Grad der Subarrays entlang einer anderen Achse multiplizieren / dividieren / addieren / subtrahieren / erhöhen müssen, müssen Sie die Transposition verwenden, um die gewünschte Achse an ihre erste Stelle zu setzen und sie dann an ihre Stelle zurückzusetzen. Betrachten Sie das obige Beispiel, jedoch mit Multiplikation mit dem Vektor B der Spalten von Array A:
A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.array([-1.1, -1.2, -1.3]) C = (AT + B).T D = (AT - B).T E = (AT * B).T F = (AT / B).T G = (AT ** B).T print('+\n', C, '\n') print('-\n', D, '\n') print('*\n', E, '\n') print('/\n', F, '\n') print('**\n', G, '\n') Out: + [[-0.1 0.9 1.9] [ 2.8 3.8 4.8] [ 5.7 6.7 7.7]] - [[ 2.1 3.1 4.1] [ 5.2 6.2 7.2] [ 8.3 9.3 10.3]] * [[ -1.1 -2.2 -3.3] [ -4.8 -6. -7.2] [ -9.1 -10.4 -11.7]] / [[-0.90909091 -1.81818182 -2.72727273] [-3.33333333 -4.16666667 -5. ] [-5.38461538 -6.15384615 -6.92307692]] ** [[1. 0.4665165 0.29865282] [0.18946457 0.14495593 0.11647119] [0.07968426 0.06698584 0.05747576]]
Für komplexere Funktionen (z. B. Trigonometrie, Exponent, Logarithmus, Umrechnung zwischen Grad und Bogenmaß, Modul, Quadratwurzel usw.) verfügt NumPy über eine Implementierung. Betrachten Sie das Beispiel von Exponential und Logarithmus: A = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 9.]]) B = np.exp(A) C = np.log(B) print('A', A, '\n') print('B', B, '\n') print('C', C, '\n') Out: A [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]] B [[2.71828183e+00 7.38905610e+00 2.00855369e+01] [5.45981500e+01 1.48413159e+02 4.03428793e+02] [1.09663316e+03 2.98095799e+03 8.10308393e+03]] C [[1. 2. 3.] [4. 5. 6.] [7. 8. 9.]]
Eine vollständige Liste der mathematischen Operationen in NumPy finden Sie hier .<up>Matrixmultiplikation
Die obige Operation des Produkts von Arrays wird elementweise ausgeführt. Und wenn Sie Operationen nach den Regeln der linearen Algebra für Arrays wie für Tensoren ausführen müssen, können Sie die Punktmethode (A, B) verwenden. Abhängig von der Art der Operanden führt die Funktion Folgendes aus:- Wenn die Argumente Skalare (Zahlen) sind, wird eine Multiplikation durchgeführt.
- Wenn die Argumente ein Vektor (eindimensionales Array) und ein Skalar sind, wird das Array mit einer Zahl multipliziert.
- Wenn die Argumente Vektoren sind, wird eine Skalarmultiplikation durchgeführt (die Summe der elementweisen Produkte).
- Wenn die Argumente Tensor (mehrdimensionales Array) und Skalar sind, wird der Vektor mit einer Zahl multipliziert.
- Wenn die Argumente des Tensors vorliegen, wird das Produkt der Tensoren entlang der letzten Achse des ersten Arguments und des vorletzten zweiten ausgeführt.
- Wenn die Argumente Matrizen sind, wird das Produkt der Matrizen ausgeführt (dies ist ein Sonderfall des Tensorprodukts).
- Wenn die Argumente Matrix und Vektor sind, werden das Produkt aus Matrix und Vektor ausgeführt (dies ist auch ein Sonderfall des Tensorprodukts).
Um die Operationen auszuführen, müssen die entsprechenden Größen übereinstimmen: für Längenvektoren, für Tensoren die Längen entlang der Achsen, entlang derer die elementweisen Produkte summiert werden.Betrachten Sie Beispiele mit Skalaren und Vektoren:
Bei Tensoren werden wir nur untersuchen, wie sich die Geometrie des resultierenden Arrays in der Größe ändert:
Um ein Tensorprodukt mit anderen Achsen anstelle der für Punkt definierten auszuführen, können Sie Tensordot mit einer expliziten Achse verwenden: A = np.ones((1, 3, 7, 4)) B = np.ones((5, 7, 6, 7, 8)) print('A:', A.shape, '\nB:', B.shape, '\nresult:', np.tensordot(A, B, [2, 1]).shape, '\n\n') Out: A: (1, 3, 7, 4) B: (5, 7, 6, 7, 8) result: (1, 3, 4, 5, 6, 7, 8)
Wir haben ausdrücklich angegeben, dass wir die dritte Achse des ersten Arrays und die zweite Achse der zweiten verwenden (die Größen entlang dieser Achsen müssen übereinstimmen).<up>Aggregatoren
Aggregatoren sind NumPy-Methoden, mit denen Sie Daten entlang einiger Achsen durch integrale Merkmale ersetzen können. Sie können beispielsweise den Durchschnittswert, das Maximum, das Minimum, die Variation oder ein anderes Merkmal entlang einer beliebigen Achse oder Achsen berechnen und aus diesen Daten ein neues Array bilden. Die Form des neuen Arrays enthält alle Achsen des ursprünglichen Arrays mit Ausnahme derjenigen, entlang derer der Aggregator gezählt wurde.Zum Beispiel bilden wir ein Array mit zufälligen Werten. Dann finden wir den minimalen, maximalen und durchschnittlichen Wert in seinen Spalten: A = np.random.rand(4, 5) print('A\n', A, '\n') print('min\n', np.min(A, 0), '\n') print('max\n', np.max(A, 0), '\n') print('mean\n', np.mean(A, 0), '\n') print('average\n', np.average(A, 0), '\n') Out: A [[0.58481838 0.32381665 0.53849901 0.32401355 0.05442121] [0.34301843 0.38620863 0.52689694 0.93233065 0.73474868] [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] [0.74758173 0.73529492 0.58517879 0.11785686 0.81204847]] min [0.09888225 0.03710514 0.17910721 0.05245685 0.00962319] max [0.74758173 0.73529492 0.58517879 0.93233065 0.81204847] mean [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039] average [0.4435752 0.37060634 0.45742049 0.35666448 0.40271039]
Bei dieser Verwendung sehen Mittelwert und Durchschnitt wie Synonyme aus. Diese Funktionen haben jedoch einen anderen Satz zusätzlicher Parameter. Es gibt verschiedene Möglichkeiten, gemittelte Daten zu maskieren und zu gewichten.Sie können die Integraleigenschaften in mehreren Achsen berechnen: A = np.ones((10, 4, 5)) print('sum\n', np.sum(A, (0, 2)), '\n') print('min\n', np.min(A, (0, 2)), '\n') print('max\n', np.max(A, (0, 2)), '\n') print('mean\n', np.mean(A, (0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]
In diesem Beispiel wird eine andere integrale charakteristische Summe betrachtet - die Summe.Die Liste der Aggregatoren sieht ungefähr so aus:- sum: sum und nansum - eine Variante, die mit nan richtig umgeht;
- Arbeit: Prod und Nanprod;
- Durchschnitt und Erwartung: Durchschnitt und Mittelwert (Nanomittel),
es gibt keinen Durchschnitt ; - Median: Median und Nanmedian;
- Perzentil: Perzentil und Nanperzentil;
- Variation: var und nanvar;
- Standardabweichung (Quadratwurzel der Variation): std und nanstd;
- : min nanmin;
- : max nanmax;
- , : argmin nanargmin;
- , : argmax nanargmax.
argmin argmax (, nanargmin, nanargmax) , .
,
. argmin argmax , - ravel().
, NumPy, : np.aggregator(A, axes) A.aggregator(axes), aggregator , axes — .
A = np.ones((10, 4, 5)) print('sum\n', A.sum((0, 2)), '\n') print('min\n', A.min((0, 2)), '\n') print('max\n', A.max((0, 2)), '\n') print('mean\n', A.mean((0, 2)), '\n') Out: sum [50. 50. 50. 50.] min [1. 1. 1. 1.] max [1. 1. 1. 1.] mean [1. 1. 1. 1.]
<>—
Lassen Sie uns einen Algorithmus für die lineare Tiefpassbildfilterung erstellen.Laden Sie zunächst ein verrauschtes Bild hoch.
Betrachten Sie ein Fragment des Bildes, um das Rauschen zu sehen:
Wir filtern das Bild mit einem Gaußschen Filter. Aber anstatt die Faltung direkt (mit Iteration) durchzuführen, wenden wir die gewichtete Mittelung von Bildschnitten an, die relativ zueinander verschoben sind: def smooth(I): J = I.copy() J[1:-1] = (J[1:-1] // 2 + J[:-2] // 4 + J[2:] // 4) J[:, 1:-1] = (J[:, 1:-1] // 2 + J[:, :-2] // 4 + J[:, 2:] // 4) return J
Wir wenden diese Funktion einmal, zweimal und dreimal auf unser Bild an: I_noise = cv2.imread('sarajevo_noise.jpg') I_denoise_1 = smooth(I_noise) I_denoise_2 = smooth(I_denoise_1) I_denoise_3 = smooth(I_denoise_2) cv2.imwrite('sarajevo_denoise_1.jpg', I_denoise_1) cv2.imwrite('sarajevo_denoise_2.jpg', I_denoise_2) cv2.imwrite('sarajevo_denoise_3.jpg', I_denoise_3)
Wir erhalten die folgenden Ergebnisse:
bei einmaliger Verwendung des Filters;
mit doppelt;
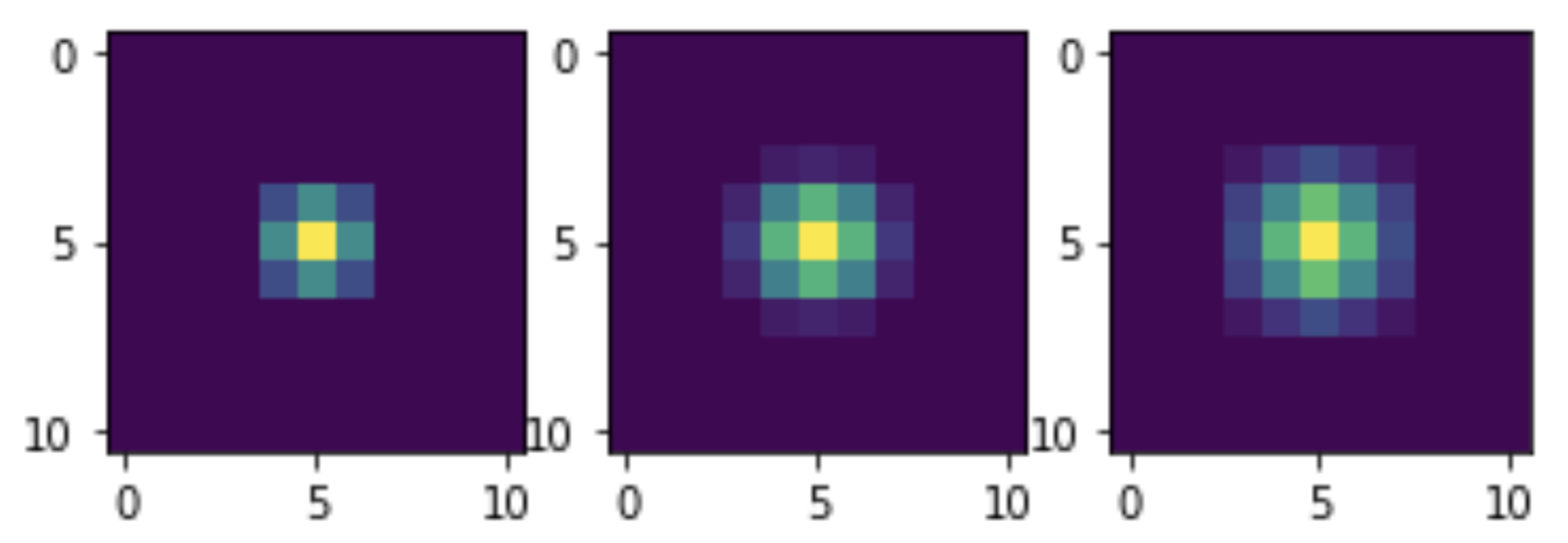
dreimal.Es ist ersichtlich, dass mit zunehmender Anzahl von Filterdurchgängen der Rauschpegel abnimmt. Dies verringert jedoch auch die Klarheit des Bildes. Dies ist ein bekanntes Problem bei linearen Filtern. Unsere Methode zum Entrauschen von Bildern erhebt jedoch keinen Anspruch auf Optimalität: Dies ist nur eine Demonstration der Fähigkeit von NumPy, Faltung ohne Iterationen zu implementieren.Nun wollen wir sehen, mit welcher Faltung unsere Filterung äquivalent ist. Dazu setzen wir einen einzelnen Einheitsimpuls ähnlichen Transformationen aus und visualisieren ihn. Tatsächlich ist der Impuls nicht einfach, sondern hat eine Amplitude von 255, da das Mischen selbst für ganzzahlige Daten optimiert ist. Dies beeinträchtigt jedoch nicht die Beurteilung des allgemeinen Erscheinungsbildes der Kerne: M = np.zeros((11, 11)) M[5, 5] = 255 M1 = smooth(M) M2 = smooth(M1) M3 = smooth(M2) plt.subplot(1, 3, 1) plt.imshow(M1) plt.subplot(1, 3, 2) plt.imshow(M2) plt.subplot(1, 3, 3) plt.imshow(M3) plt.show()
Wir haben uns vorgenommen, die NumPy-Funktionen bei weitem nicht vollständig zu nutzen. Ich hoffe, dies hat ausgereicht, um die volle Leistungsfähigkeit und Schönheit dieses Tools zu demonstrieren!<up>