Kürzlich wurde ein Artikel mit dem nicht so faszinierenden Titel "
Neuronale Neuparametrisierung verbessert Strukturoptimierung " auf arXiv.org hochgeladen [arXiv: 1909.04240]. Es stellte sich jedoch heraus, dass die Autoren tatsächlich eine sehr nicht triviale Methode zur Verwendung eines neuronalen Netzwerks entwickelten, um eine Lösung für das Problem der strukturellen / topologischen Optimierung physikalischer Modelle zu erhalten (obwohl die Autoren selbst sagen, dass die Methode universeller ist). Der Ansatz ist sehr merkwürdig, produktiv und scheint völlig neu zu sein (ich kann jedoch nicht für Letzteres bürgen, aber weder für die Autoren der Arbeit noch für die ODS-Community, noch könnte ich mich an Analoga erinnern). Daher kann es nützlich sein, dies für diejenigen zu wissen, die an der Verwendung neuronaler Netze interessiert sind. sowie das Lösen verschiedener Optimierungsprobleme.
Worüber sprichst du? Was ist die Aufgabe der topologischen Optimierung?
Stellen Sie sich vor, was Sie zum Beispiel benötigen, um einen Brückenfaden, ein mehrstöckiges Gebäude, einen Flugzeugflügel, ein Turbinenblatt oder was auch immer zu entwerfen. In der Regel wird dies gelöst, indem ein Spezialist gefunden wird, z. B. ein Architekt, der sein Wissen über Matan, Sopromat, das Zielgebiet sowie seine Erfahrung, Intuition, Testlayouts usw. nutzt. usw. würde das gewünschte Projekt erstellen. Hier ist es wichtig, dass dieses erhaltene Projekt nur den Besten dieses Spezialisten zugute kommt. Und das ist natürlich nicht immer genug. Als Computer leistungsfähig genug wurden, versuchten wir daher, solche Aufgaben auf sie zu verlagern. Denn
es ist offensichtlich, was ein Computer im Speicher behalten und kurzschließen kann ... warum nicht?
Solche Aufgaben werden "strukturelle Optimierungsprobleme" genannt, d.h. Erzeugung einer optimalen Auslegung tragender mechanischer Strukturen [1]. Ein Unterabschnitt von Strukturoptimierungsproblemen sind
topologische Optimierungsprobleme (tatsächlich konzentriert sich die fragliche Arbeit speziell auf sie, aber dies ist absolut nicht der Punkt, und dazu später mehr). Ein typisches topologisches Optimierungsproblem sieht ungefähr so aus: Für ein bestimmtes Konzept (Brücke, Haus usw.) im Raum in zwei oder drei Dimensionen, mit spezifischen Einschränkungen in Form von Materialien, Technologien und anderen Anforderungen, mit einigen externen Lasten, müssen Sie entwerfen Eine optimale Struktur, die Lasten hält und Einschränkungen erfüllt.
- "Entwerfen" bedeutet im Wesentlichen, einen Unterraum des Quellraums zu finden / beschreiben, der mit Baumaterial gefüllt werden muss.
- Optimalität kann zum Beispiel in Form einer Anforderung ausgedrückt werden, das Gesamtgewicht der Struktur unter Einschränkungen in Form der maximal zulässigen Spannungen im Material und möglicher Verschiebungen bei gegebenen Lasten zu minimieren.
Um dieses Problem auf einem Computer zu lösen, wird der Ziellösungsraum in eine Reihe von finiten Elementen (Pixel für 2D und Voxel für 3D) abgetastet. Anschließend entscheidet der Computer mithilfe eines Algorithmus, ob dieses einzelne Element mit Material gefüllt oder leer gelassen werden soll.

(Bild aus "Entwicklungen in der Topologie und Formoptimierung", Chau Hoai Le, 2010)
Schon aus der Erklärung des Problems geht hervor, dass seine Lösung für Wissenschaftler ein ziemlich großer Splitter ist. Ich kann denjenigen, die einige Details wünschen, beispielsweise einen sehr alten (2010, der für ein sich aktiv entwickelndes Gebiet noch viel ist), aber eine ziemlich detaillierte und leicht zu googelnde Chau Hoai Le-Dissertation mit dem Titel "Entwicklungen in der Topologie und Formoptimierung" [2] anbieten, von wo aus Ich habe die oberen und unteren Bilder gestohlen.
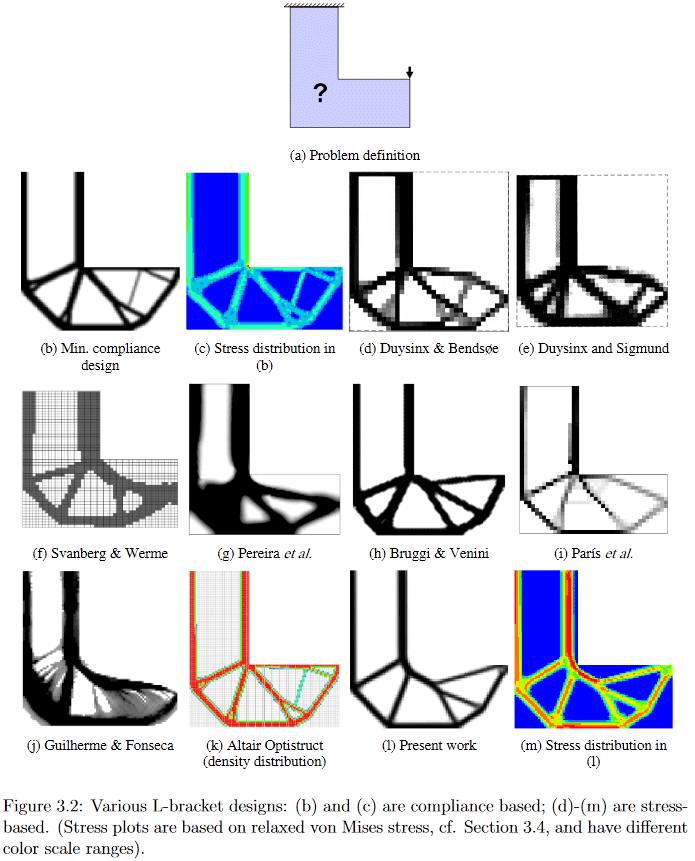
(Bild aus "Entwicklungen in der Topologie und Formoptimierung", Chau Hoai Le, 2010)
In diesem Bild können Sie beispielsweise deutlich sehen, wie sehr unterschiedliche Algorithmen eine Lösung für das scheinbar einfache Designproblem der L-förmigen Aufhängung erzeugen.
Nun zurück zur fraglichen Arbeit.
Die Autoren schlugen sehr witzig vor, solche Optimierungsprobleme zu lösen, indem sie eine Kandidatenlösung durch ein neuronales Netzwerk und die anschließende Entwicklung der Lösung durch Gradientenabstiegsmethoden in Bezug auf die objektive Compliance-Funktion generierten. Die Übereinstimmung der resultierenden Struktur wird unter Verwendung eines differenzierbaren physikalischen Modells geschätzt, das tatsächlich die Verwendung eines Gradientenabfalls ermöglicht. Ihnen zufolge (die Autoren haben die
Quellcodes von [5] veröffentlicht) ergibt dies entweder das gleiche Ergebnis wie die besten traditionellen Algorithmen für einfache Probleme oder die besten dieser Algorithmen, die als Basis für komplexe Probleme verwendet werden.
Methode
Als nächstes werde ich versuchen zu beschreiben, was und wie genau die Autoren vorgeschlagen haben, aber ich warne sofort, dass ich keine 100% ige Korrektheit garantiere, da ich zusätzlich zu meiner extrem rostigen Gelehrsamkeit auf dem Gebiet zusätzlich zu der äußerst mageren Kürze der Beschreibung eine allgemeine "Unreife" des Artikels hinzufügen sollte. Das, gemessen am Vorhandensein von zwei Ausgaben in 4 Tagen, wird gerade fertiggestellt (
hinzugefügt: Im Moment glaube ich, dass zumindest im Grunde alles richtig beschrieben wird).
Die Autoren verfolgen im Allgemeinen den Ansatz zur Lösung solcher Optimierungsprobleme, der als „modifizierte SIMP-Methode“ bezeichnet wird und in [3] „Effiziente Topologieoptimierung in MATLAB mit 88 Codezeilen“ ausführlich beschrieben wird. Der Preprint dieser Arbeit und der damit verbundene Code finden Sie unter
http://www.topopt.mek.dtu.dk/Apps-and-software/Efficient-topology-optimization-in-MATLAB . Diese Arbeit wird häufig verwendet, um Schüler über topologische Optimierungsprobleme zu unterrichten. Um sie besser zu verstehen, wird daher empfohlen, sich damit vertraut zu machen.
Bei „modifiziertem SIMP“ wird die Lösung direkt optimiert, indem die Pixel des Bildes mit physikalischer Dichte geändert werden. Die Autoren der Arbeit schlugen nicht vor, das Bild direkt zu modifizieren (obwohl ein solcher Algorithmus bei sonst gleichen Bedingungen ein Kontrollalgorithmus war), sondern die Parameter und Eingaben des Faltungs-Neuronalen Netzwerks zu ändern, das ein Bild der physikalischen Dichte erzeugt. So sieht die gesamte Methode global aus:

(Bild aus der betreffenden Publikation)
Schritt 1, Generieren eines Kandidaten
Ein neuronales Netzwerk (im Folgenden als NS bezeichnet), das den zufälligen primären Eingabevektor _beta verwendet (es ist wie das Netzwerkgewicht ein trainierter Parameter), erzeugt (einige) Bilder der Lösung (es funktioniert mit 2D, aber in 3D kann es meiner Meinung nach auch verteilt werden ) Der Upsampling-Teil der bekannten U-Net-Architektur wird als NS-Generator verwendet.
Schritt 2: Anwenden von Einschränkungen und Konvertieren eines Kandidaten in ein physisches Modell-Framework
Pixelwerte werden in zwei Schritten in physikalische Dichten umgewandelt:
- Zunächst wird in einem Schritt das Problem der Normalisierung der nicht normalisierten Werte der generierten Pixel gelöst (der NS ist so ausgelegt, dass er die sogenannten Logits - Werte im Bereich (-inf, + inf) ausgibt) und Einschränkungen für die Gesamtmenge der resultierenden Lösung angewendet. Hierzu wird ein Sigmoid elementweise auf das Bild angewendet, dessen Argument in Abhängigkeit von dem zu transformierenden Bild und dem Volumen der gewünschten Lösung um eine Konstante verschoben wird (der Wert dieser Vorspannungskonstante wird durch binäre Suche so ausgewählt, dass das Gesamtvolumen der so erhaltenen Dichten gleich einem bestimmten vorbestimmten Volumen wäre V0). Eine detaillierte Analyse dieser Phase, siehe Kommentar );
- Ferner wird das resultierende normalisierte Bild der Dichten der Struktur von den sogenannten verarbeitet ein Dichtefilter mit einem Radius von 2. Bekannter ist dieser Filter nichts anderes als ein normalgewichteter Durchschnitt benachbarter Punkte im Bild. Die Gewichte in diesem Filter (Filterkern) können als Werte der Höhen von Punkten dargestellt werden, die sich auf der Oberfläche eines regulären Kegels befinden, der auf der Ebene liegt, so dass sein Scheitelpunkt am aktuellen Punkt liegt. Daher nennen die Autoren ihn Kegelfilter (ausführlicher zu diesem Thema) siehe Beschreibung des Dichtefilters in Kapitel 2.3 Filterung von [3]).
Kurz gesagt, das Wesentliche des gesamten Schritts 2 ist, dass sich die nicht normalisierte Ausgabe eines völlig normalen NS in einen richtig normalisierten, leicht geglätteten Rahmen des physikalischen Modells (eine Reihe physikalischer Dichten von Elementen) verwandelt, auf den bereits die erforderlichen Einschränkungen von vornherein angewendet wurden (dies ist die Menge des verwendeten Materials).
Schritt 3, Bewertung des resultierenden physikalischen Rahmenmodells
Das resultierende Gerüst wird durch einen differenzierbaren physikalischen Motor geführt, um den Vektor (/ Tensor?) Der strukturellen Verschiebung unter Last (einschließlich Schwerkraft) U zu erhalten. Der Schlüssel hier ist die Differenzierbarkeit des Motors, die es uns ermöglicht, Gradienten zu erhalten (ich erinnere mich, dass der Gradient der Funktion im Allgemeinen ist Ein Tensor, der aus partiellen Ableitungen einer Funktion in Bezug auf alle ihre Argumente besteht. Der Gradient zeigt die Richtung und Änderungsrate der Funktion am aktuellen Punkt. Wenn Sie dies wissen, können Sie die Argumente so "verdrehen", dass die gewünschte Änderung mit der Funktion auftritt - es nahm ab oder zu). Solch eine differenzierbare physische Engine muss nicht von Grund auf neu geschrieben werden - sie existiert seit langem und ist bekannt. Die Autoren mussten ihre Paarung nur mit Berechnungspaketen für neuronale Netze wie TensorFlow / PyTorch durchführen.
Schritt 4: Berechnen des Werts der Zielfunktion für das Drahtmodell / den Kandidaten
Die zu minimierende skalare Zielfunktion c (x) wird berechnet, die die Übereinstimmung (es ist die Umkehrung der Steifigkeit) des resultierenden Gerüsts beschreibt. Die Compliance-Funktion hängt vom Verschiebungsvektor U ab, der im letzten Schritt erhalten wurde, und von der Steifigkeitsmatrix der Struktur K (ich habe nicht genügend Kenntnisse über die Topologieoptimierung, um zu verstehen, woher K kommt - ich gehe davon aus, dass dies direkt aus dem Framework betrachtet wird).
/ *
siehe auch Kommentare
(1) von
kxx und
(2) von
350 Stealth , obwohl es sich lohnt, zur grundlegenden Erleuchtung zu gehen [3].
* /
Und dann ist es geschafft. Da alles in einer Umgebung mit automatischer Differenzierung erstellt wird, erhalten wir in diesem Stadium automatisch alle Gradienten der Zielfunktion, die aufgrund der Differenzierbarkeit aller Transformationen bei jedem Schritt auf die Gewichte und den Eingabevektor des erzeugenden neuronalen Netzwerks zurückgeschoben werden. Die Gewichte bzw. der Eingabevektor mit ihren partiellen Ableitungen ändern sich und verursachen die notwendige Änderung - wodurch die Zielfunktion minimiert wird. Als nächstes tritt ein neuer Zyklus des direkten Durchgangs durch die NS auf -> Anwendung von Beschränkungen -> Berechnung des physikalischen Modells -> Berechnung der Zielfunktion -> neue Gradienten und Aktualisierung der Gewichte. Und so weiter bis zur Konvergenz von Algo.
Ein wichtiger Punkt, dessen Beschreibung ich in der Arbeit nicht gefunden habe, ist die Auswahl des Gesamtvolumens der Konstruktion V0, mit deren Hilfe die Kandidatenlösung in Schritt 2 in das Framework konvertiert wird. Offensichtlich hängen die Eigenschaften der resultierenden Lösung stark von ihrer Wahl ab. Durch indirekte Angaben (alle Beispiele der erhaltenen Lösungen [4] unterscheiden sich in mehreren Fällen genau in der Volumenbegrenzung) gehe ich davon aus, dass sie V0 einfach auf einem bestimmten Gitter aus dem Bereich [0,05, 0,5] fixieren und dann die erhaltenen Lösungen mit unterschiedlichen Augen betrachten V0. Nun, für eine konzeptionelle Arbeit ist dies im Allgemeinen ausreichend, obwohl es natürlich furchtbar interessant wäre, auch bei der Auswahl dieser V0 eine Option zu sehen, aber es wird wahrscheinlich in die nächste Entwicklungsstufe der Arbeit übergehen.
Der zweite wichtige Punkt, den ich nicht verstanden habe, ist, wie sie Einschränkungen / Anforderungen für die spezifische Art der Lösung auferlegen. Das heißt, Wenn Sie die Brücke dank des physischen Modells immer noch vom Gebäude trennen können (das Gebäude hat volle Unterstützung und die Brücke befindet sich nur an den Grenzenden), wie kann man dann beispielsweise ein Gebäude mit 3 Etagen von einem Gebäude mit 4 Etagen trennen?
Wie funktioniert es
Es stellte sich heraus, dass das Verfahren für kleine Probleme (in Bezug auf die Größe des Lösungsraums = Anzahl der Pixel) ± die gleiche Qualität der Ergebnisse liefert wie die besten herkömmlichen Methoden zur topologischen Optimierung, jedoch für große (Gittergröße von 2 ^ 15 oder mehr Pixeln, d. H. Zum Beispiel ist es ab 128 * 256 und mehr wahrscheinlicher, qualitativ hochwertige Lösungen mit der Methode zu erhalten als mit der besten traditionellen (von 116 getesteten Problemen ergab die Methode eine bevorzugte Lösung bei 99 Problemen gegenüber 66 bevorzugten bei der besten traditionellen).
Außerdem beginnt hier etwas besonders Interessantes. Traditionelle Methoden zur topologischen Optimierung bei großen Problemen leiden unter der Tatsache, dass sie in den frühen Arbeitsphasen schnell ein kleines Netz bilden, das dann die Entwicklung großer Strukturen stört. Dies führt zu der Tatsache, dass das erhaltene Ergebnis schwierig / unmöglich physikalisch umzusetzen ist. Daher gibt es bei Problemen mit der Topologieoptimierung zwangsweise eine ganze Richtung, in der Methoden untersucht / entwickelt werden, wie die resultierenden Lösungen technologisch bequemer gestaltet werden können.
Hier erfolgt offenbar dank des Faltungsnetzwerks gleichzeitig eine Optimierung auf mehreren räumlichen Skalen gleichzeitig, wodurch das "Web" vermieden / stark reduziert und einfachere, aber qualitativ hochwertige und technologisch freundliche Lösungen erhalten werden können!
Darüber hinaus werden dank der Faltung des Netzwerks grundlegend andere Lösungen erhalten als bei herkömmlichen Standardmethoden.
Zum Beispiel in Designs:
- Cantilever-Beam-Methode fand eine Lösung von nur 8 Komponenten, während die beste traditionelle - 18.
- Die Methode der dünnen Stützbrücke wählte eine Stütze mit einem baumartigen Verzweigungsmuster, während die traditionelle ein - zwei Stützen
- Bei der Dachmethode werden Säulen verwendet, während bei der herkömmlichen Methode ein Verzweigungsmuster verwendet wird. Usw.
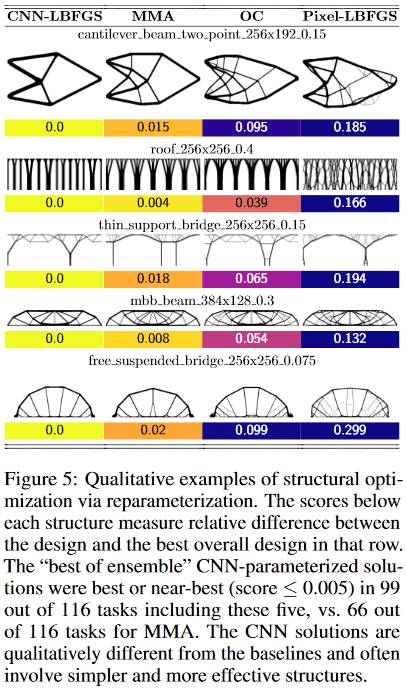
(Bild aus der betreffenden Publikation)
Was ist das Besondere an dieser Arbeit?
Ich habe noch nie eine solche Verwendung eines neuronalen Netzwerks gesehen. Typischerweise werden neuronale Netze verwendet, um eine sehr knifflige und komplexe Funktion y = F (x, Theta) zu erhalten (wobei x das Argument und Theta die einstellbaren Parameter sind), die etwas Nützliches bewirken kann. Wenn x beispielsweise ein Bild von der Kamera eines Autos ist, kann der y-Wert der Funktion beispielsweise ein Zeichen dafür sein, ob sich ein Fußgänger in gefährlicher Nähe des Autos befindet. Das heißt, Hierbei ist es wichtig, dass die jeweilige Art von Funktion selbst, die wiederholt zur Lösung eines Problems verwendet wird, wertvoll ist.
Hier wird das neuronale Netzwerk als gerissener Repository-Modifikator-Einsteller von Parametern eines physikalischen Modells verwendet, der aufgrund seiner Architektur bestimmte Einschränkungen für die Werte und Variationen von Änderungen dieser Parameter auferlegt (tatsächlich sind die Beispiele unter der Überschrift Pixel-LBFGS ein Versuch, Pixel direkt zu optimieren, nicht Wenn Sie ein neuronales Netzwerk verwenden, um sie zu generieren, sind die Ergebnisse sichtbar. Der NS ist wichtig. Hier wird die Faltung des verwendeten neuronalen Netzwerks kritisch, da Sie mit seiner Architektur das Konzept der Übertragungsinvarianz und einer kleinen Rotation „erfassen“ können (stellen Sie sich vor, Sie erkennen Text aus einem Bild - es ist wichtig, dass Sie den Text extrahieren, und es spielt keine Rolle, welcher Teile des Bildes, es befindet sich und wie es gedreht wird - das heißt, Sie benötigen die Invarianz der Übertragung und Drehung). Bei diesem Problem bleibt eine Art physischer Stab, der eine Struktureinheit darstellt und von dem viele optimiert werden, unabhängig von seiner Position und Ausrichtung im Raum erhalten.
Ein klassisches vollständig verbundenes Netzwerk zum Beispiel würde hier wahrscheinlich nicht funktionieren (genauso gut), weil seine Architektur zu viel / zu wenig zulässt (na ja, so ein Dualismus, wie man aussieht). Gleichzeitig ist es uns bei dieser Aufgabe trotz der Tatsache, dass der NS hier die sehr, sehr knifflige und komplexe Funktion y = F (x, Theta) bleibt, egal, ob es sich um sein Argument x und seine Parameter Theta handelt und wie die Funktion verwendet wird. Wir sind nur besorgt über seinen Einzelwert y, der bei der Optimierung einer bestimmten Zielfunktion für ein bestimmtes physikalisches Modell erhalten wird, bei dem {x, Theta} nur konfigurierbare Parameter sind!
Dies ist meiner Meinung nach eine unglaublich coole und neue Idee! (obwohl sich dann natürlich wie immer herausstellen kann, dass Schmidhuber es Anfang der 90er Jahre beschrieben hat, aber wir werden abwarten und sehen)
Im Allgemeinen erinnert die Bedeutung der Methode etwas an verstärktes Lernen - dort wird der NS grob gesagt als „Erfahrungsspeicher“ eines Agenten verwendet, der in einer bestimmten Umgebung handelt, und aktualisiert, wenn die Umgebung Feedback zu den Aktionen des Agenten erhält. Nur dort wird dieses „Repository of Experience“ ständig verwendet, um neue Entscheidungen des Agenten zu treffen, und hier ist es nur ein Repository von Parametern des physikalischen Modells, von dem wir nur an dem einzigen Endergebnis der Optimierung interessiert sind.
Nun, der letzte. Ein interessanter Moment fiel mir auf.
So sehen optimale Lösungen für die Aufgabe eines mehrstöckigen Gebäudes aus:
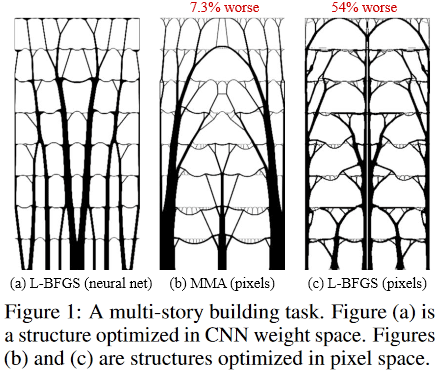
(Bild aus der betreffenden Publikation)
Und so:

Es befindet sich in der fantastischen Sagrada Familia, dem Tempel der Heiligen Familie in Barcelona, Spanien, der vom brillanten Antonio Gaudi „entworfen“ wurde.
Danksagung
Ich danke dem Erstautor des Artikels, Stephan Hoyer, für die schnelle Unterstützung bei der Erläuterung einiger dunkler Details der Arbeit sowie den Habr-Teilnehmern, die ihre Ergänzungen und / oder nützlichen provokativen Ideen vorgenommen haben.
[1]
Option zur Bestimmung des strukturellen / topologischen Optimierungsproblems[2]
"Entwicklungen in der Topologie und Formoptimierung"[3] Andreassen, E., Clausen, A., Schevenels, M., Lazarov, BS und Sigmund, O. Effiziente Topologieoptimierung in MATLAB unter Verwendung von 88 Codezeilen. Strukturelle und multidisziplinäre Optimierung, 43 (1): 1–16, 2011. Ein Preprint dieser Arbeit und dieses Codes ist unter
http://www.topopt.mek.dtu.dk/Apps-and-software/Efficient-topology-optimization-in verfügbar
-MATLAB[4]
Beispiele für Arbeitslösungen[5] Arbeitscodes:
https://github.com/google-research/neural-structural-optimization
Siehe auch
Letzte Aktualisierung dieser Publikation 2020.01.23 09:18