Arend - HoTT-basierte abhängige Typensprache (Teil 1)

In diesem Beitrag werden wir über die neu veröffentlichte JetBrains-Sprache mit Arend-abhängigen Typen sprechen (die Sprache ist nach Gating Rent benannt ). Diese Sprache wurde in den letzten Jahren von JetBrains Research entwickelt. Obwohl die Repositories vor einem Jahr auf github.com/JetBrains öffentlich zugänglich gemacht wurden, erfolgte die vollständige Veröffentlichung von Arend erst im Juli dieses Jahres.

Wir werden versuchen herauszufinden, wie sich Arend von bestehenden Systemen der formalisierten Mathematik unterscheidet, die auf abhängigen Typen basieren, und welche Funktionen den Benutzern jetzt zur Verfügung stehen. Wir gehen davon aus, dass der Leser dieses Artikels im Allgemeinen mit abhängigen Typen vertraut ist und mindestens eine der auf abhängigen Typen basierenden Sprachen gehört hat: Agda, Idris, Coq oder Lean. Wir erwarten jedoch nicht, dass der Leser abhängige Typen auf fortgeschrittenem Niveau hat.

Der Einfachheit und Konkretheit halber wird unsere Geschichte über Arend- und Homotopietypen von der Implementierung des einfachsten Listensortieralgorithmus auf Arend begleitet - selbst bei diesem Beispiel können Sie den Unterschied zwischen Arend und Agda und Coq spüren. Es gibt bereits eine Reihe von Artikeln über Habré, die sich mit abhängigen Typen befassen. Angenommen, über die Implementierung von Sortierlisten mit der QuickSort-Methode auf Agda gibt es einen solchen Artikel . Wir werden einen einfacheren Algorithmus zum Sortieren von Inserts implementieren. In diesem Fall konzentrieren wir uns auf die Konstruktionen der Arend-Sprache und nicht auf den Sortieralgorithmus selbst.

Der Hauptunterschied zwischen Arend und anderen Sprachen mit abhängigen Typen ist also die logische Theorie, auf der es basiert. Arend verwendet als solches die kürzlich entdeckte Homotopietypentheorie ( HoTT ) von V. Voevodsky . Insbesondere basiert Arend auf einer Variation von HoTT, die als "Typentheorie mit Abstand" bezeichnet wird. Es sei daran erinnert, dass Coq auf der sogenannten Berechnung induktiver Konstruktionen (Berechnung induktiver Konstruktionen) basiert, während Agda und Idris auf der Martin-Löf-Intensionstheorie der Typen basieren. Die Tatsache, dass Arend auf HoTT basiert, beeinflusst seine syntaktischen Konstruktionen und die Funktionsweise des Typprüfungsalgorithmus (Typcheker) erheblich. Wir werden diese Funktionen in diesem Artikel diskutieren.

Versuchen wir kurz den Zustand der Sprachinfrastruktur zu beschreiben. Für Arend gibt es ein Plugin für IntelliJ IDEA, das direkt aus dem Repository der IDEA-Plugins installiert werden kann. Im Prinzip reicht die Installation des Plugins aus, um vollständig mit Arend zu arbeiten. Sie müssen dennoch nichts herunterladen und installieren. Zusätzlich zur Typprüfung bietet das Arend-Plugin Funktionen, die IDEA-Benutzern vertraut sind: Hervorheben und Ausrichten des Codes, verschiedene Refactorings und Tipps. Es besteht auch die Möglichkeit, die Konsolenversion von Arend zu verwenden. Eine detailliertere Beschreibung des Installationsvorgangs finden Sie hier .

Die Codebeispiele in diesem Artikel basieren auf der Arend-Standardbibliothek. Wir empfehlen daher, den Quellcode aus dem Repository herunterzuladen. Nach dem Herunterladen muss das Quellverzeichnis mit dem Befehl Projekt importieren als IDEA-Projekt importiert werden. Bei Arend wurden bereits einige Abschnitte der Homotopietypentheorie und der Ringtheorie formalisiert. Zum Beispiel gibt es in der Standardbibliothek eine Implementierung des Rings der rationalen Zahlen Q zusammen mit Beweisen aller erforderlichen ring-theoretischen Eigenschaften.

Eine ausführliche Sprachdokumentation , in der viele der in diesem Artikel behandelten Punkte ausführlicher erläutert werden, ist ebenfalls gemeinfrei. Sie können Arend-Entwicklern im Telegrammkanal direkt Fragen stellen.

1. Übersicht über HoTT / Arend

Die Homotopietypentheorie (oder kurz HoTT) ist eine Art von Intensionstyptheorie, die sich von der klassischen Martin-Löf-Typentheorie (MLTT, auf der Agda basiert) und der Berechnung induktiver Konstruktionen (CIC, auf der Coq basiert) darin unterscheidet Anweisungen und Mengen enthalten die sogenannten Typen einer höheren Homotopieebene.

In diesem Artikel setzen wir uns nicht das Ziel, die Grundlagen von HoTT im Detail zu erklären - für eine detaillierte Darstellung dieser Theorie wäre es notwendig, das gesamte Buch erneut zu erzählen (siehe diesen Beitrag ). Wir stellen nur fest, dass eine Theorie, die auf der Axiomatik von HoTT basiert, in gewissem Sinne viel eleganter und interessanter ist als die klassische Martin-Löf-Typentheorie. So werden in HoTT eine Reihe von Axiomen, die zuvor zusätzlich postuliert werden mussten (z. B. funktionale Extensionalität), als Theoreme bewiesen. Darüber hinaus kann man in HoTT intern mehrdimensionale Homotopiekugeln definieren und sogar einige ihrer Homotopiegruppen zählen .

Diese Aspekte von HoTT sind jedoch in erster Linie für Mathematiker interessant, und der Zweck dieses Artikels besteht darin, zu erklären, wie sich das HoTT-basierte Arend im Vergleich zu Agda / MLTT und Coq / CIC günstig verhält, indem beispielsweise Programmiererentitäten so einfach und vertraut wie geordnete Listen dargestellt werden. Wenn Sie diesen Artikel lesen, reicht es aus, HoTT als eine Art Intensivtyp-Theorie mit einer weiter entwickelten Axiomatik zu behandeln, die die Arbeit mit Universen und Gleichheiten erleichtert.

1.1 Abhängige Typen, Curry-Howard-Korrespondenz, Universen

Denken Sie daran, dass sich Sprachen mit abhängigen Typen von normalen funktionalen Programmiersprachen dadurch unterscheiden, dass es zusätzlich zu den üblichen Datentypen wie Listen oder natürlichen Zahlen Typen gibt, die vom Parameterwert abhängen. Die einfachsten Beispiele für solche Typen sind Vektoren einer gegebenen Länge n oder ausgeglichene Bäume einer gegebenen Tiefe d. Einige weitere Beispiele für solche Typen werden hier erwähnt .

Denken Sie daran, dass die Curry-Howard-Korrespondenz es erlaubt, Aussagen der Logik als abhängige Typen zu interpretieren. Die Hauptidee dieser Entsprechung ist, dass ein leerer Typ einer falschen Aussage entspricht und aufgefüllte Typen einer wahren Aussage entsprechen. Typelemente können als Beweise für die entsprechende logische Aussage angesehen werden. Beispielsweise kann jedes Element wie Ganzzahlen als Beweis dafür angesehen werden, dass Ganzzahlen vorhanden sind (dh der Typ der Ganzzahlen wird ausgefüllt).

Unterschiedliche natürliche Konstruktionen über Typen entsprechen unterschiedlichen logischen Verknüpfungen:

• Das Produkt der Typen A × B wird manchmal als Typ des Paares Paar A B bezeichnet. Da dieser Typ genau dann ausgefüllt wird, wenn beide Typen A und B ausgefüllt sind, entspricht diese Konstruktion dem logischen „und“.
• Die Summe der Typen A + B. In Haskell wird dieser Typ entweder A B genannt. Da dieser Typ genau dann ausgefüllt wird, wenn einer der Typen A oder B ausgefüllt ist, entspricht diese Konstruktion einem logischen „oder“.
  
• Funktionstyp A → B. Jede Funktion dieses Typs wandelt Elemente von A in Elemente von B um. Somit existiert eine solche Funktion genau dann, wenn die Existenz eines Elements vom Typ A die Existenz eines Elements vom Typ B impliziert. Daher entspricht diese Konstruktion der Implikation.
  

Nehmen wir nun an, wir erhalten einen bestimmten Typ A und eine Familie von Typen B, die durch ein Element a vom Typ A parametrisiert sind. Geben wir Beispiele für komplexere Konstruktionen über abhängige Typen.

• Abhängiger Funktionstyp Π (a: A) (B a). Dieser Typ stimmt mit dem üblichen Funktionstyp A → B überein, wenn B unabhängig von A ist. Eine Funktion vom Typ Π (a: A) (B a) wandelt jedes Element a vom Typ A in ein Element vom Typ B a um. Eine solche Funktion existiert also genau dann, wenn für a : A ein Element B a existiert. Daher entspricht diese Konstruktion dem universellen Quantifizierer ∀. Für den abhängigen Funktionstyp verwendet Arend die Syntax \Pi (x : A) -> B a , und der Begriff, der diesen Typ bewohnt, kann mit dem Lambda-Ausdruck \lam (a : A) => f a. konstruiert werden \lam (a : A) => f a.
• Die Art der abhängigen Paare ist Σ (a: A) (B a). Dieser Typ stimmt mit den üblichen Typen von A × B-Paaren überein, wenn B unabhängig von A ist. Der Typ Σ (a: A) (B a) wird genau dann gefüllt, wenn ein Element a: A und ein Element vom Typ B a vorhanden sind. Somit entspricht dieser Typ dem Existenzquantifizierer ∃ . Der Typ der abhängigen Paare in Arend wird mit \Sigma (a : A) (B a) , und die Begriffe, die ihn bewohnen, werden unter Verwendung des Konstruktors des (abhängigen) Paares (a, b) konstruiert.
  
• Der Typ der Gleichheit ist a = a ', wobei a und a' zwei Elemente eines Typs A sind. Ein solcher Typ wird gefüllt, wenn a und a 'gleich sind, und ist ansonsten leer. Offensichtlich ist dieser Typ ein Analogon des Gleichheitsprädikats in der Logik.

An dieser Stelle verweisen wir den Leser auf Quellen, in denen die Curry-Howard-Korrespondenz ausführlicher besprochen wird (siehe beispielsweise einen Kurs von Vorlesungen oder Artikeln hier oder hier ).

Alle in der Typentheorie berücksichtigten Ausdrücke müssen einen Typ haben. Da Ausdrücke, die Typen bezeichnen, im Rahmen dieser Theorie ebenfalls berücksichtigt werden, muss ihnen auch ein bestimmter Typ zugewiesen werden. Die Frage ist, was für ein Typ sollte es sein?

Die erste naive Entscheidung, die mir in den Sinn kommt, besteht darin, allen Typen einen formalen Typ \Type zuzuweisen, der als Universum bezeichnet wird (er wird so genannt, weil er im Allgemeinen alle Typen enthält). Wenn wir dieses Universum verwenden, erhalten die oben genannten Summenkonstruktionen und Typprodukte die Signatur \Type → \Type → \Type , und komplexere Konstruktionen des abhängigen Produkts und die abhängige Summe erhalten die Signatur Π (A : \Type) → ((A → \Type) → \Type) .

An dieser Stelle stellt sich die Frage, welchen Typ das \Type Universum selbst haben soll. Ein naiver Versuch zu sagen, dass der Typ des Universums \Type per Definition \Type selbst ist, führt zum Girard-Paradoxon. Betrachten Sie also anstelle eines einzelnen Universums \Type eine unendliche Hierarchie von Universen , d. H. Die verschachtelte Kette von Universen \Type 1 < \Type 2 < … , deren Ebenen durch natürliche Zahlen nummeriert sind, und der Typ des Universums \Type i ist per Definition das Universum \Type (i+1) . Für die oben genannten Typkonstruktionen müssen auch komplexere Signaturen eingeführt werden.

Daher werden Universen in der Typentheorie benötigt, damit jeder Ausdruck einen bestimmten Typ hat. In einigen Varianten der Typentheorie werden Universen für einen anderen Zweck verwendet: zur Unterscheidung zwischen Arten von Typen. Wir haben bereits gesehen, dass Mengen und Anweisungen Sonderfälle von Typen sind. Dies zeigt, dass es möglicherweise sinnvoll ist, ein separates Prop-Universum für Anweisungen und eine separate Hierarchie von Set- _i- Universen für Sets in die Theorie einzuführen. Dies ist genau der Ansatz, der in Calculus of Inductive Constructions verwendet wird, der Theorie, auf der das Coq-System basiert.

1.2 Beispiele für einfachste induktive Typen und rekursive Funktionen

Betrachten Sie die Definitionen der einfachsten induktiven Datentypen in Arend: Boolescher Typ, natürlicher Zahlentyp und polymorphe Listen. Arend verwendet das Schlüsselwort \data , um neue induktive Typen einzuführen.

\data Empty -- ,

\data Bool
| true
| false

\data Nat
| zero
| suc Nat

\data List (A : \Set)
| nil
| \infixr 5 :-: A (List A)

Wie Sie den obigen Beispielen entnehmen können, müssen Sie nach dem Schlüsselwort \data den Namen des induktiven Typs und eine Liste seiner Konstruktoren angeben. Gleichzeitig können der Datentyp und die Konstruktoren einige Parameter haben. Angenommen, im obigen Beispiel hat der List einen Parameter A Der nil hat keine Parameter, und der Konstruktor: -: hat zwei Parameter (von denen einer vom Typ A und der andere vom Typ List A ). Das Universum \Set besteht aus Typen, die Mengen sind (die Definition der Mengen wird im nächsten Abschnitt angegeben). Mit \infixr können Sie die Infix-Notation für den Konstruktor verwenden: -: und teilt dem Arend-Parser außerdem mit, dass der Operator: -: eine \infixr Operation mit Priorität 5 ist.

In Arend beginnen alle Schlüsselwörter mit einem Backslash-Zeichen ("\"), einer von LaTeX inspirierten Implementierung. Beachten Sie nur, dass die lexikalischen Regeln in Arend sehr liberal sind: Circle_HSpace, contrFibers=>Equiv, suc/=0, zro_*-left und sogar n:Nat - all diese Literale sind Beispiele für gültige Bezeichner in Arend. Das letzte Beispiel zeigt, wie wichtig es für den Arend-Benutzer ist , Leerzeichen zwischen Bezeichnern und Doppelpunktzeichen einzufügen . Beachten Sie, dass in Arend-Bezeichnern keine Unicode-Zeichen verwendet werden dürfen (insbesondere können Sie kein Kyrillisch verwenden).

Arend verwendet das Schlüsselwort \func , um Funktionen zu definieren. Die Syntax dieser Konstruktion lautet wie folgt: Nach dem Schlüsselwort \func müssen Sie den Namen der Funktion, ihre Parameter und den Typ des Rückgabewerts angeben. Das letzte Element bei der Definition einer Funktion ist ihr Körper.

Wenn es möglich ist, den Ausdruck, in dem die angegebene Funktion berechnet werden soll, explizit anzugeben, wird zur Angabe des Funktionskörpers das Token => verwendet. Betrachten Sie zum Beispiel die Definition einer Typnegationsfunktion.

 \func Not (A : \Type) : \Type => A -> Empty 

Der Rückgabetyp einer Funktion muss nicht immer explizit angegeben werden. Im obigen Beispiel könnte Arend unabhängig auf den Typ Not , und wir könnten den Ausdruck ": \Type " nach den Klammern weglassen.

Wie in den meisten formalisierten Mathematiksystemen muss der Benutzer keine explizite Vorhersageebene für das \Type Universum angeben, und Definitionen, in denen Universen ohne explizite Angabe einer Vorhersageebene verwendet werden, werden als polymorph angesehen .

Versuchen wir nun, eine Funktion zu definieren, die die Länge der Liste berechnet. Eine solche Funktion ist durch Mustervergleich leicht zu identifizieren. Arend verwendet hierfür das Schlüsselwort \elim . Danach müssen Sie die Variablen angeben, mit denen der Vergleich durchgeführt wird (wenn es mehr als eine solche Variable gibt, sollten sie mit einem Komma geschrieben werden). Wenn der Vergleich für alle expliziten Parameter durchgeführt wird, kann \elim zusammen mit den Variablen weggelassen werden. Das Folgende ist ein Block von Vergleichspunkten, die durch einen vertikalen Balken "|" voneinander getrennt sind. Jedes Element in diesem Block ist ein Ausdruck der Form «, » => «» .

 \func length {A : \Set} (l : List A) : Nat | nil => 0 | :-: x xs => suc (length xs) 

Im obigen Beispiel ist Parameter A der Längenfunktion von geschweiften Klammern umgeben. Diese Klammern in Arend werden verwendet, um implizite Argumente zu bezeichnen, d.h. Argumente, die der Benutzer beim Aufrufen einer Funktion oder beim Verwenden eines Typs weglassen kann. Beachten Sie, dass Sie in Arend die Infix-Notation nicht verwenden können, um Konstruktoren beim Abgleich mit einem Muster zu bestimmen. Daher wird im Beispielbeispiel die Präfixnotation verwendet.

Wie in Coq / Agda müssen in Arend alle Funktionen garantiert abgeschlossen sein (d. H. In Arend ist eine Terminierungsprüfung vorhanden). Bei der Definition der Längenfunktion ist diese Prüfung erfolgreich, da ein rekursiver Aufruf das erste explizite Argument streng reduziert. Wenn eine solche Reduzierung nicht auftreten würde, würde Arend eine Fehlermeldung ausgeben.

 \func bad : Nat => bad [ERROR] Termination check failed for function 'bad' In: bad 

Arend ermöglicht zirkuläre Abhängigkeiten und gegenseitig rekursive Funktionen, für die auch Abschlussprüfungen durchgeführt werden. Der Algorithmus dieser Prüfung basiert auf dem Artikel von A. Abel. Darin finden Sie eine detailliertere Beschreibung der Bedingungen, die gegenseitig rekursive Funktionen erfüllen müssen.

1.3 Wie unterscheiden sich Mengen von Aussagen?

Wir haben zuvor geschrieben, dass Beispiele für Typen Mengen und Anweisungen sind. Darüber hinaus haben wir die Schlüsselwörter \Type und \Set , um Universen in Arend zu bezeichnen. In diesem Abschnitt werden wir versuchen, detaillierter zu erklären, wie sich Aussagen in Bezug auf Varietäten der Intensitätstypentheorie (MLTT, CIC, HoTT) von Mengen unterscheiden, und gleichzeitig zu erklären, woraus die Bedeutung der Schlüsselwörter \Prop , \Set und \Type in Arend besteht.

Denken Sie daran, dass es in der klassischen Martin-Löf-Theorie keine Trennung von Typen in Mengen und Aussagen gibt. Insbesondere gibt es theoretisch nur ein kumulatives Universum (das entweder mit Set in Agda oder Type in Idris oder Sort in Lean bezeichnet wird). Dieser Ansatz ist der einfachste, aber es gibt Situationen, in denen sich seine Mängel manifestieren. Angenommen, wir versuchen, den Typ "geordnete Liste" als abhängiges Paar zu implementieren, das aus einer Liste und einem Nachweis seiner Reihenfolge besteht. Es stellt sich heraus, dass es dann im Rahmen des „reinen“ MLTT nicht möglich sein wird, die Gleichheit geordneter Listen zu beweisen, die aus identischen Elementen bestehen, die sich gleichzeitig in Begriffen der Ordnungsnachweise unterscheiden. Eine solche Gleichheit wäre sehr natürlich und wünschenswert, so dass die Unmöglichkeit, sie zu beweisen, als theoretischer Fehler in der MLTT angesehen werden kann.

In Agda wird dieses Problem teilweise mit Hilfe von sogenannten Annotationen der Immaterialität gelöst (siehe Quelle , in der das Listenbeispiel ausführlicher besprochen wird). Diese Annotationen sind jedoch weder ein Konstrukt aus der MLTT-Theorie noch vollwertige Konstrukte für Typen (es ist unmöglich, sie mit einer Typanmerkung zu markieren, die im Funktionsargument nicht verwendet wird).

In CIC, basierend auf CIC, sind zwei verschiedene Universen ineinander verschachtelt: Prop (das Universum der Aussagen) und Set (das Universum der Mengen), die in die umfassende Hierarchie der Type eingetaucht sind. Der Hauptunterschied zwischen Prop und Set besteht darin, dass es eine Reihe von Einschränkungen für Variablen gibt, deren Typ zu Prop in Coq gehört. Zum Beispiel können sie nicht für Berechnungen verwendet werden, und ein Vergleich mit der Stichprobe für sie ist nur innerhalb der Beweise anderer Aussagen möglich. Auf der anderen Seite sind alle Elemente des Typs, die zum Prop Universum gehören, im Axiom unwichtiger Beweise gleich, siehe die Aussage in Coq.Logic.ProofIrrelevance . Mit diesem Axiom könnten wir leicht die Gleichheit der oben genannten geordneten Listen beweisen.

Betrachten Sie abschließend den Arend / HoTT-Ansatz für Aussagen und Universen. Der Hauptunterschied besteht darin, dass HoTT auf das Axiom unwichtiger Beweise verzichtet. Das heißt, es gibt in HoTT kein spezielles Axiom, das postuliert, dass alle Elemente von Anweisungen gleich sind. In HoTT ist ein Typ per Definition eine Aussage, wenn nachgewiesen werden kann, dass alle seine Elemente einander gleich sind. Wir können ein Prädikat für Typen definieren, das wahr ist, wenn der Typ eine Anweisung ist:

 \func isProp (A : \Type) => \Pi (aa' : A) -> a = a' 

Es stellt sich die Frage: Welche Typen erfüllen dieses Prädikat, dh sind Aussagen? Es ist leicht zu überprüfen, ob dies für leere und Singleton-Typen gilt. Für Typen, bei denen mindestens zwei verschiedene Elemente vorhanden sind, gilt dies nicht mehr.

Natürlich möchten wir, dass alle notwendigen logischen Verknüpfungen über die Anweisungen definiert werden. In Abschnitt 1.1 haben wir bereits diskutiert, wie sie mit typentheoretischen Konstruktionen bestimmt werden können. Es gibt jedoch das folgende Problem: Nicht alle von uns eingegebenen isProp behalten die isProp Eigenschaft bei. Konstruktionen des Produktprodukts und des (abhängigen) Funktionstyps behalten diese Eigenschaft bei, während die Konstruktionen der Summe von Typen und abhängigen Paaren dies nicht tun. Daher können wir die Disjunktion und den Quantifizierer der Existenz nicht verwenden.

Dieses Problem kann mit Hilfe einer neuen Konstruktion gelöst werden, die zu HoTT hinzugefügt wird, der sogenannten Satzkürzung . Mit diesem Design können Sie jeden Typ in eine Anweisung verwandeln. Es kann als formale Operation betrachtet werden, bei der alle Begriffe, die in diesem Typ vorkommen, gleich sind. Diese Operation ähnelt den Annotationen der Immaterialität von Agda, ist jedoch im Gegensatz zu ihnen eine vollwertige Operation für Typen mit der Signatur \Type -> \Prop .

Das letzte wichtige Beispiel für Aussagen ist die Gleichheit zweier Elemente eines Typs. Es stellt sich heraus, dass im allgemeinen Fall die Art der Gleichheit a = a' keine Aussage sein muss. Die Typen, für die es einer ist, werden Mengen genannt:

 \func isSet (A : \Type) => \Pi (aa' : A) -> isProp (a = a') 

Alle Typen, die in gewöhnlichen Programmiersprachen vorkommen, erfüllen dieses Prädikat, dh Gleichheit auf ihnen ist eine Aussage. Dies gilt beispielsweise für natürliche Zahlen, Ganzzahlen, Produkte von Mengen, Summen von Mengen, Funktionen über Mengen, Listen von Mengen und andere induktive Datentypen, die aus Mengen aufgebaut sind. Das heißt, wenn wir nur an solchen bekannten Konstruktionen interessiert sind, können wir nicht an beliebige Typen denken, die dieses Prädikat nicht erfüllen. Alle in Coq gefundenen Typen sind Mengen .

Typen, die keine Mengen sind, werden nützlich, wenn Sie sich mit der Homotopietypentheorie befassen möchten. Im Moment verweisen wir den Leser einfach auf das Standardbibliotheksmodul, das die Definition einer n-dimensionalen Kugel enthält , ein Beispiel für einen Typ, der keine Menge ist.

Arend hat spezielle Universen \Prop und \Set , die aus Anweisungen bzw. Mengen bestehen. Wenn wir bereits wissen, dass Typ A im Universum \Prop (oder \Set ) enthalten ist, kann der Beweis der entsprechenden isProp (oder isSet ) isSet in Arend mithilfe des im Vorspiel integrierten Path.inProp Axioms erhalten werden (wir geben ein Beispiel für die Verwendung dieses Axioms) in Abschnitt 2.3).

 \func inProp {A : \Prop} : \Pi (aa' : A) -> a = a' 

Wir haben bereits festgestellt, dass nicht alle natürlichen Konstrukte auf Typen die isProp Eigenschaft beibehalten. Beispielsweise erfüllen induktive Datentypen mit zwei oder mehr Konstruktoren dies nie. Wie oben erwähnt, können wir das Satzkürzungskonstrukt verwenden, das jeden Typ in eine Anweisung verwandelt.
In der Arend-Bibliothek heißt die Standardimplementierung der Logic.TruncP . Wir könnten einen Typ von logischem "oder" in Arend so definieren, dass die Summe der Typen abgeschnitten wird:

 \data \fixr 2 Or (AB : \Type) -- Sum of types; analogue of Coq's type "sum" | inl A | inr B \func \infixr 2 || (AB : \Type) => TruncP (sum AB) -- Logical “or”, analogue of Coq's type "\/" 

In Arend gibt es eine andere, einfachere und bequemere Möglichkeit, einen propositionell abgeschnittenen induktiven Typ zu definieren. Fügen Sie dazu einfach das Schlüsselwort \truncated bevor Sie den Datentyp definieren. Beispielsweise wird die Definition eines logischen "oder" in der Arend-Standardbibliothek wie folgt angegeben.

 \truncated \data \infixr 2 || (AB : \Type) : \Prop -- Logical “or”, analogue of Coq's type "\/" | byLeft A | byRight B 

Weitere Arbeiten mit propositionell abgeschnittenen Typen ähneln denen von Typen, die dem Prop Universum in Coq zugeordnet sind. Beispielsweise ist der Mustervergleich einer Variablen, deren Typ eine Anweisung ist, nur in einer Situation zulässig, in der der Typ des zu definierenden Ausdrucks selbst eine Anweisung ist. Somit ist es immer einfach, die Funktion Or-to-|| zu definieren durch Vergleich mit der Stichprobe, aber die Umkehrfunktion dazu, nur wenn der Typ A `Or` B eine Aussage ist (was selten genug ist, zum Beispiel wenn Typ A und B beide Aussagen sind und sich gegenseitig ausschließen).

 \func Or-to-|| {AB : \Prop} (a-or-b : A `Or` B) : A || B | inl a => byLeft a | inr b => byRight 

Denken Sie auch daran, dass die Besonderheit des Mechanismus der Universen in Coq darin besteht, dass, wenn dem Prop Universum eine Definition zugewiesen wurde, diese in keiner Weise für die Berechnung verwendet werden kann. Aus diesem Grund empfehlen die Coq-Entwickler selbst nicht die Verwendung von Satzkonstruktionen, sondern empfehlen, diese nach Möglichkeit durch Analoga aus dem Universum der Mengen zu ersetzen. Der Mechanismus von Arend-Universen hat diesen Nachteil nicht, dh in bestimmten Situationen ist es möglich, Aussagen in Berechnungen zu verwenden. Wir werden ein Beispiel für eine solche Situation geben, wenn wir die Implementierung des Listensortierungsalgorithmus diskutieren.

1.4 Klassen in Arend

Da unser Ziel darin besteht, den einfachsten Sortieralgorithmus zu implementieren, erscheint es sinnvoll, sich mit der Implementierung der in der Arend-Standardbibliothek verfügbaren geordneten Mengen vertraut zu machen.

In Arend werden Klassen verwendet, um Operationen und Axiome zu kapseln, die mathematische Strukturen definieren, und um die Beziehungen zwischen diesen Strukturen mithilfe der Vererbung hervorzuheben. Klassen sind auch Namespaces, in denen es zweckmäßig ist, Konstruktionen und Theorien zu platzieren, deren Bedeutung angemessen ist.

Die Basisklasse, von der alle Auftragsklassen in Arend geerbt werden, ist die BaseSet Klasse, die keine anderen BaseSet als die Bezeichnung E für den BaseSet enthält (d. H. Den Satz, für den BaseSet Nachkommenklassen bereits verschiedene Operationen einführen). Betrachten Sie die Definition dieser Klasse aus der Standard-Arend-Bibliothek.

 \class BaseSet (E : \Set) -- ,     

In der obigen Definition wird Träger E als Klassenparameter deklariert. Man kann sich fragen, gibt es einen Unterschied in der obigen Definition von BaseSet von der folgenden Definition, in der Träger E als Klassenfeld definiert ist?

 \class BaseSet' --      | E : \Set 

Eine etwas unerwartete Antwort ist, dass es in Arend keinen Unterschied zwischen den beiden Definitionen gibt, da jeder Klassenparameter (auch implizit) in Arend tatsächlich sein Feld ist. Daher könnte man für beide BaseSet Implementierungen den Ausdruck xE um auf das Feld E zuzugreifen. BaseSet immer noch einen Unterschied zwischen den obigen Varianten der BaseSet Definition, aber es ist subtiler, wir werden ihn im nächsten Abschnitt genauer untersuchen, wenn wir Klasseninstanzen diskutieren ( Klasseninstanzen).

Das Sortieren einer Liste ist nur dann sinnvoll, wenn für den Objekttyp in der Liste eine lineare Reihenfolge angegeben ist. Daher betrachten wir zunächst die Definitionen einer streng teilweise geordneten Menge und einer linear geordneten Menge.

 \class StrictPoset \extends BaseSet { | \infix 4 < : E -> E -> \Prop | <-irreflexive (x : E) : Not (x < x) | <-transitive (xyz : E) : x < y -> y < z -> x < z } \class LinearOrder \extends StrictPoset { | <-comparison (xyz : E) : x < z -> x < y || y < z | <-connectedness (xy : E) : Not (x < y) -> Not (y < x) -> x = y } 

Aus Sicht der Typentheorie können Klassen in Arend als Analoga von Sigma-Typen mit einer bequemeren Syntax für Projektionen und Konstruktoren betrachtet werden. , Arend- -, .

, . , . , StrictPoset <-irreflexive <-transitive , E < — . , (, , ) , .

, , . , Arend , , . , . , , , , . :

 \class DecSet \extends BaseSet | decideEq (xy : E) : Dec (x = y) 

Dec , Dec E , E , E , E .

 \data Dec (E : \Prop) | yes E | no (Not E) 

, , Dec ( decidable) Order.LinearOrder . Dec , , , trichotomy , , E , <. , Dec Comparable Java.

 \class Dec \extends LinearOrder, DecSet { | trichotomy (xy : E) : (x = y) || (x < y) || (y < x) | <-comparison xyz x<z => {?} --   | <-connectedness xyx/<yy/<x => {?} | decideEq xy => {?} } 

Dec Dec , , , , . Dec , .

, Dec ( ). Dec , Arend ( Dec LinearOrder, DecSet ), , (diamond inheritance).

: , ( , ).

Dec Order.LinearOrder IDEA ( [Ctrl]+[H]), , .



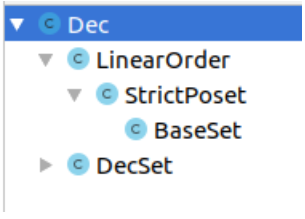
Arend ( IDEA BaseSet ). , .

1.5 , , .

StrictPoset Nat. Arend , . -, , , - ( ), .

: . .

 data \infix 4 < (ab : Nat) \with | zero, suc _ => zero<suc_ | suc a, suc b => suc<suc (a < b) \lemma irreflexivity (x : Nat) (p : x < x) : Empty | suc a, suc<suc a<a => irreflexivity a a<a \lemma transitivity (xyz : Nat) (p : x < y) (q : y < z) : x < z | zero, suc y', suc z', zero<suc_, suc<suc y'<z' => zero<suc_ | suc x', suc y', suc z', suc<suc x'<y', suc<suc y'<z' => suc<suc (transitivity x' y' z' x'<y' y'<z') 

\func \lemma . , , , . , \lemma , \Prop .

x'<y' — -, x' < y' . - (.. , , ).

(instance) StrictPoset . Arend . \new . « ».

 \func NatOrder => \new StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity } 

StrictPoset { … } \new : - StrictPoset . - , , , \new . \new C { … } C { … } . C, C. , , NatOrder StrictPoset .

, . , StrictPoset Nat StrictPoset { | E => Nat } . , NatOrder StrictPoset , ( ).

NatOrder \cowith ( - ).

 \func NatOrder : StrictPoset \cowith { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity } 

, , \instance.

 \instance NatOrder : StrictPoset { | E => Nat | < => < | <-irreflexive => irreflexivity | <-transitive => transitivity } 

Arend , Haskell. NatOrder \instance \cowith , StrictPoset ( ).

, BaseSet - E ( ), , E . .

, Arend . Arend , , ( , « » \classifying \field , Arend ). :

• Arend . , X StrictPoset , List X List XE .
  
• Arend .

, . , \instance StrictPoset , Nat Int ( NatOrder IntOrder ).

, x < y , x, y , , x, y . Arend , NatOrder.< , — IntOrder.< .

, . Arend , < StrictPoset , E. , Arend x<y StrictPoset ( ), E . , < .

, Arend. , \use \coerce . Arend — , , . - , \where .

. fromNat .

 \data Int | pos Nat | neg Nat \with { zero => pos zero } \where { \use \coerce fromNat (n : Nat) => pos n } 

\use \coerce \func , . , , (, , ).

: HoTT JetBrains Research.